diff options
| author | Christian Kolset <christian.kolset@gmail.com> | 2025-03-17 12:26:40 -0600 |
|---|---|---|
| committer | Christian Kolset <christian.kolset@gmail.com> | 2025-03-17 12:26:40 -0600 |
| commit | 7be45360e1131945f2c43182358da252ee07edac (patch) | |
| tree | 688168306217b06ff806ba3ae26a21c982caa567 /tutorials/1_06_arrays.md | |
| parent | 646fabeb7d614ca39f7ee6c260a9f9c9183c7e54 (diff) | |
Completed tutorials. Finished the arrays and control_structures tutorials. Still need touch up but the first iteration is complete.
Diffstat (limited to 'tutorials/1_06_arrays.md')
| -rw-r--r-- | tutorials/1_06_arrays.md | 95 |
1 files changed, 94 insertions, 1 deletions
diff --git a/tutorials/1_06_arrays.md b/tutorials/1_06_arrays.md index 76dd1ee..c8f2452 100644 --- a/tutorials/1_06_arrays.md +++ b/tutorials/1_06_arrays.md @@ -12,11 +12,15 @@ A two-dimensional array would be like a table: | 8 | 3 | 6 | 1 | | 1 | 7 | 2 | 9 | -A three-dimensional array would be like a set of tables, perhaps stacked as though they were printed on separate pages. +A three-dimensional array would be like a set of tables, perhaps stacked as though they were printed on separate pages. If we visualize the position of each element as a position in space. Then we can represent the value of the element as a property. In other words, if we were to analyze the stress concentration of an aluminum block, the property would be stress. - From [Numpy documentation](https://numpy.org/doc/2.2/user/absolute_beginners.html) +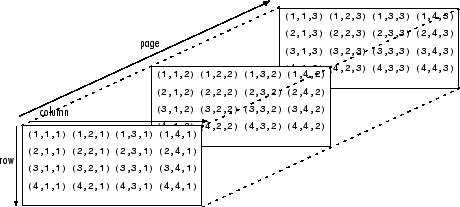 + +If the load on this block changes over time, then we may want to add a 4th dimension i.e. additional sets of 3-D arrays for each time increment. As you can see - the more dimensions we add, the more complicated of a problem we have to solve. It is possible to increase the number of dimensions to the n-th order. This course we will not be going beyond dimensional analysis. --- +# Numpy - the python's array library In this tutorial we will be introducing arrays and we will be using the numpy library. Arrays, lists, vectors, matrices, sets - You might've heard of them before, they all store data. In programming, an array is a variable that can hold more than one value at a time. We will be using the Numpy python library to create arrays. Since we already have installed Numpy previously, we can start using the package. @@ -30,6 +34,7 @@ import numpy as np - `import` - calls for a library to use, in our case it is Numpy. - `as` - gives the library an alias in your script. It's common convention in Python programming to make the code shorter and more readable. We will be using *np* as it's a standard using in many projects. +--- # Creating arrays Now that we have imported the library we can create a one dimensional array or *vector* with three elements. ```python @@ -48,6 +53,7 @@ matrix = np.array([[1,2,3], *Note: for every array we nest, we get a new dimension in our data structure.* ## Numpy array creation functions +Numpy comes with some built-in function that we can use to create arrays quickly. Here are a couple of functions that are commonly used in python. ### np.arange The `np.arange()` function returns an array with evenly spaced values within a specified range. It is similar to the built-in `range()` function in Python but returns a Numpy array instead of a list. The parameters for this function are the start value (inclusive), the stop value (exclusive), and the step size. If the step size is not provided, it defaults to 1. @@ -74,3 +80,90 @@ Try this and see what happens: x = np.linspace(0,100,101) y = np.sin(x) ``` + +### Other useful functions +- `np.zeros()` +- `np.ones()` +- `np.eye()` + +## Working with Arrays +Now that we have been introduced to some ways to create arrays using the Numpy functions let's start using them. +### Indexing +Indexing in Python allows you to access specific elements within an array based on their position. This means you can directly retrieve and manipulate individual items as needed. + +Python uses **zero-based indexing**, meaning the first element is at position **0** rather than **1**. This approach is common in many programming languages. For example, in a list with five elements, the first element is at index `0`, followed by elements at indices `1`, `2`, `3`, and `4`. + +Here's an example of data from a rocket test stand where thrust was recorded as a function of time. + +```python +thrust_lbf = np.array(0.603355, 2.019083, 2.808092, 4.054973, 1.136618, 0.943668) + +>>> thrust_lbs[3] +``` + +Due to the nature of zero-based indexing. If we want to call the value `4.054973` that will be the 3rd index. +### Operations on arrays +- Arithmetic operations (`+`, `-`, `*`, `/`, `**`) +- `np.add()`, `np.subtract()`, `np.multiply()`, `np.divide()` +- `np.dot()` for dot product +- `np.matmul()` for matrix multiplication +- `np.linalg.inv()`, `np.linalg.det()` for linear algebra +#### Statistics +- `np.mean()`, `np.median()`, `np.std()`, `np.var()` +- `np.min()`, `np.max()`, `np.argmin()`, `np.argmax()` +- Summation along axes: `np.sum(arr, axis=0)` +#### Combining arrays +- Concatenation: `np.concatenate((arr1, arr2), axis=0)` +- Stacking: `np.vstack()`, `np.hstack()` +- Splitting: `np.split()` + +# Exercise +Let's solve a statics problem given the following problem + +A simply supported bridge of length L=20L = 20L=20 m is subjected to three point loads: + +- $P1=10P_1 = 10P1=10 kN$ at $x=5x = 5x=5 m$ +- $P2=15P_2 = 15P2=15 kN$ at $x=10x = 10x=10 m$ +- $P3=20P_3 = 20P3=20 kN$ at $x=15x = 15x=15 m$ + +The bridge is supported by two reaction forces at points AAA (left support) and BBB (right support). We assume the bridge is in static equilibrium, meaning the sum of forces and sum of moments about any point must be zero. + +#### Equilibrium Equations: + +1. **Sum of Forces in the Vertical Direction**: + $RA+RB−P1−P2−P3=0R_A + R_B - P_1 - P_2 - P_3 = 0RA+RB−P1−P2−P3=0$ +2. **Sum of Moments About Point A**: + $5P1+10P2+15P3−20RB=05 P_1 + 10 P_2 + 15 P_3 - 20 R_B = 05P1+10P2+15P3−20RB=0$ +3. **Sum of Moments About Point B**: + $20RA−15P3−10P2−5P1=020 R_A - 15 P_3 - 10 P_2 - 5 P_1 = 020RA−15P3−10P2−5P1=0$ + +#### System of Equations: + +{RA+RB−10−15−20=05(10)+10(15)+15(20)−20RB=020RA−5(10)−10(15)−15(20)=0\begin{cases} R_A + R_B - 10 - 15 - 20 = 0 \\ 5(10) + 10(15) + 15(20) - 20 R_B = 0 \\ 20 R_A - 5(10) - 10(15) - 15(20) = 0 \end{cases}⎩ + + +## Solution +```python +import numpy as np + +# Define the coefficient matrix A +A = np.array([ + [1, 1], + [0, -20], + [20, 0] +]) + +# Define the right-hand side vector b +b = np.array([ + 45, + 5*10 + 10*15 + 15*20, + 5*10 + 10*15 + 15*20 +]) + +# Solve the system of equations Ax = b +x = np.linalg.lstsq(A, b, rcond=None)[0] # Using least squares to handle potential overdetermination + +# Display the results +print(f"Reaction force at A (R_A): {x[0]:.2f} kN") +print(f"Reaction force at B (R_B): {x[1]:.2f} kN") +```
\ No newline at end of file |
