diff options
| author | Christian Kolset <christian.kolset@gmail.com> | 2025-09-05 12:27:55 -0600 |
|---|---|---|
| committer | Christian Kolset <christian.kolset@gmail.com> | 2025-09-05 12:27:55 -0600 |
| commit | 2922d7290750ed0ff08f4fc6ddee4794cb696742 (patch) | |
| tree | 97e49e1e07f50e7e233eea3454ef8b23b7136dc1 | |
| parent | 1c2ed0dc18362edf27ec14c5e45de1caaa3dfc0c (diff) | |
Finished up Bisection content
| -rw-r--r-- | tutorials/module_3/2_roots_optimization.md | 83 | ||||
| -rw-r--r-- | tutorials/module_3/roots_assignment2_data.csv | 136 |
2 files changed, 201 insertions, 18 deletions
diff --git a/tutorials/module_3/2_roots_optimization.md b/tutorials/module_3/2_roots_optimization.md index 9734d40..83684d5 100644 --- a/tutorials/module_3/2_roots_optimization.md +++ b/tutorials/module_3/2_roots_optimization.md @@ -1,11 +1,12 @@ # Root Finding Methods -Root Finding Methods or non-linear equation solvers. +By now you've learned the quadratic formula to find the roots of a second degree polynomial. +$$ +x=\frac{-b \pm \sqrt{b^2-4ac}}{2a} +$$ +This works nicely if we're given the function $f(x)$. However, how would you solve for $x$ if you were given experimental data? In this section we will cover bracketing and open methods to find roots of a function. - -In this section we will cover four different methods to find a root of a function. Let us take a step back and think algorithmically. To find a root numerically, we can implement a search algorithm. - -Let's consider a phone book - a database of names and numbers sorted alphabetically by last name. Our goal is to find the phone number of James Watt (our root). We could make an algorithm that starts at the the first page, checks to see if the current name equals our target (Watt), if it doesn't, check the next entry. This is method is called *incremental search*. As you may see, this can take very long if the database is very large. +Let us take a step back and think *algorithmically*. To find a root numerically, we can implement a search algorithm. Let's consider a small phone book - a database of names and numbers sorted alphabetically by last name. Our goal is to find the phone number of James Watt (our root). We could make an algorithm that starts at the the first page, checks to see if the current name equals our target (Watt), if it doesn't, check the next entry. This is method is called *incremental search*. As you may see, this can take very long if the database is large. > [!NOTE] Example Phonebook Database Entries > **A** – Archimedes @@ -34,46 +35,62 @@ Let's consider a phone book - a database of names and numbers sorted alphabetica > **Y** – Yukawa > **Z** – Zuse -Another approach may be to index the book and jump straight to the 'W' names however this requires two steps. Let us introduce *Bisection*. +Another approach may be to index the book and jump straight to the 'W' names however this requires two steps. + +When + +# Bracketing Method ## Incremental Search Incremental search ## Bisection -This method start by sectioning the database into two halves. We can do this with a phone book by simply opening it in the middle of the book. In our data set, we have find the middle entry to be 'M - Maxwell'. Since all names are sorted alphabetically we can conclude that we will find our target in the second half, essentially eliminating the first half. Doing this a second time gives us our new midpoint 'S – Schrödinger' and a third time get us to our target 'W - Watt'. In only 3 iterations we have reached out target goal. This is a huge improvement from the Incremental search (22 iterations) versus our new 3 iterations. +This method start by sectioning the database into two halves. We can do this with a phone book by simply opening it in the middle of the book. In our data set, we have find the middle entry to be 'M - Maxwell'. Based on the premises that all names are sorted alphabetically we can conclude that we will find our target in the second half, essentially eliminating the first half. Doing this a second time gives us our new midpoint 'S – Schrödinger' and a third time get us to our target 'W - Watt'. In only 3 iterations we have reached out target goal. This is a huge improvement from the Incremental search (22 iterations) versus our new 3 iterations. + +This exact same concept can be applied to finding roots of functions. Instead of searching for strings we are searching for floats. For computers this is a lot easier to do. Take a moment to think about how you would write psuedo-code to program this. + +> The **Intermediate Value Theorem** says that if f(x) is a continuous function between a and b, and sign(f(a))≠sign(f(b)), then there must be a c, such that a<c<b and f(c)=0. -This exact same concept can be applied to finding roots of functions. Instead of comparing strings we are comparing floats. For computers this is a lot easier to do. Take a moment to think about how you would program this. +Let's consider a continuous function $f(x)$ with an unknown root $x_r$ . Using the intermediate value theorem we can bracket a root with the points $x_{lower}$ and $x_{upper}$ such that $f(x_{lower})$ and $f(x_{upper})$ have opposite signs. This idea is visualized in the graph below. +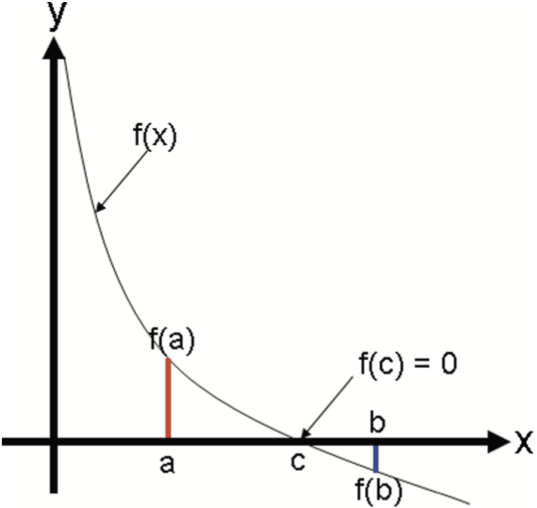 + +Once we bisect the interval and found we set the new predicted root to be in the middle. We can then compare the two sections and see if there is a sign change between the bounds. Once the section with the sign change has been identified, we can repeat this process until we near the root. + +![[Pasted image 20250905120647.png|500]] +As you the figure shows, the predicted root $x_r$ get's closer to the actual root each iteration. In theory this is an infinite process that can keep on going. In practice, computer precision may cause error in the result. A work-around to these problems is setting a tolerance for the accuracy. As engineers it is our duty to determine what the allowable deviation is. + +So let's take a look at how we can write this in python. ```python import numpy as np -def my_bisection(f, a, b, tol): +def my_bisection(f, x_l, x_u, tol): # approximates a root, R, of f bounded # by a and b to within tolerance # | f(m) | < tol with m the midpoint # between a and b Recursive implementation # check if a and b bound a root - if np.sign(f(a)) == np.sign(f(b)): + if np.sign(f(x_l)) == np.sign(f(x_u)): raise Exception( - "The scalars a and b do not bound a root") + "The scalars x_l and x_u do not bound a root") # get midpoint - m = (a + b)/2 + x_r = (x_l + x_u)/2 - if np.abs(f(m)) < tol: + if np.abs(f(x_r)) < tol: # stopping condition, report m as root - return m - elif np.sign(f(a)) == np.sign(f(m)): + return x_r + elif np.sign(f(x_l)) == np.sign(f(x_r)): # case where m is an improvement on a. # Make recursive call with a = m - return my_bisection(f, m, b, tol) - elif np.sign(f(b)) == np.sign(f(m)): + return my_bisection(f, x_r, x_u, tol) + elif np.sign(f(x_l)) == np.sign(f(x_r)): # case where m is an improvement on b. # Make recursive call with b = m - return my_bisection(f, a, m, tol) + return my_bisection(f, x_l, x_r, tol) ``` ### Example @@ -90,9 +107,39 @@ print("f(r1) =", f(r1)) print("f(r01) =", f(r01)) ``` + +### Assignment 2 +Write an algorithm that uses a combination of the bisection and incremental search to find multiple roots in the first 8 minutes of the data set. +```python +import pandas as pd +import matplotlib.pyplot as plt + +# Read the CSV file into a DataFrame called data +data = pd.read_csv('your_file.csv') + +# Plot all numeric columns +data.plot() + +# Add labels and show plot +plt.xlabel("Time (min)") +plt.ylabel("Strain (kPa)") +plt.title("Data with multiple roots") +plt.legend() +plt.show() +``` +# Open Methods ## Modified Secant We can do better. ## Newton-Raphson + + +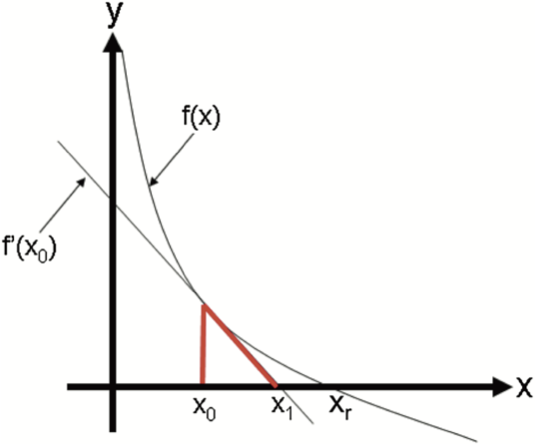 + + + +# Pipe Friction Example + +Numerical methods for Engineers 7th Edition Case study 8.4.
\ No newline at end of file diff --git a/tutorials/module_3/roots_assignment2_data.csv b/tutorials/module_3/roots_assignment2_data.csv new file mode 100644 index 0000000..34f2b69 --- /dev/null +++ b/tutorials/module_3/roots_assignment2_data.csv @@ -0,0 +1,136 @@ +0,-6219.984621
+0.05,-4769.882473
+0.1,-3420.854958
+0.15,-2175.500153
+0.2,-1035.148991
+0.25,0
+0.3,930.7538881
+0.35,1758.806199
+0.4,2486.625192
+0.45,3117.349288
+0.5,3654.689401
+0.55,4102.837919
+0.6,4466.384094
+0.65,4750.235601
+0.7,4959.546019
+0.75,5099.648023
+0.8,5175.992024
+0.85,5194.090068
+0.9,5159.464748
+0.95,5077.602918
+1,4953.914001
+1.05,4793.692677
+1.1,4602.085745
+1.15,4384.062959
+1.2,4144.391636
+1.25,3887.614854
+1.3,3618.033037
+1.35,3339.688743
+1.4,3056.354487
+1.45,2771.523399
+1.5,2488.402562
+1.55,2209.908851
+1.6,1938.667105
+1.65,1677.010476
+1.7,1426.982795
+1.75,1190.342794
+1.8,968.5700456
+1.85,762.8724619
+1.9,574.1952179
+1.95,403.2309574
+2,250.4311482
+2.05,116.0184542
+2.1,0
+2.15,-97.81859734
+2.2,-177.8185465
+2.25,-240.5526659
+2.3,-286.729744
+2.35,-317.1985842
+2.4,-332.931835
+2.45,-335.0097082
+2.5,-324.6036768
+2.55,-302.9602468
+2.6,-271.3848883
+2.65,-231.2262111
+2.7,-183.8604624
+2.75,-130.6764243
+2.8,-73.06078099
+2.85,-12.38402451
+2.9,50.01303787
+2.95,112.8321142
+3,174.829541
+3.05,234.8276264
+3.1,291.7251758
+3.15,344.5071557
+3.2,392.2534554
+3.25,434.1467111
+3.3,469.4791583
+3.35,497.6584867
+3.4,518.212671
+3.45,530.7937582
+3.5,535.180595
+3.55,531.2804817
+3.6,519.1297451
+3.65,498.8932246
+3.7,470.8626721
+3.75,435.4540675
+3.8,393.203857
+3.85,344.7641264
+3.9,290.8967233
+3.95,232.4663471
+4,170.4326306
+4.05,105.8412383
+4.1,39.81401424
+4.15,-26.46178786
+4.2,-91.74515267
+4.25,-154.7537869
+4.3,-214.1773925
+4.35,-268.6916788
+4.4,-316.9730593
+4.45,-357.7139747
+4.5,-389.6387801
+4.55,-411.5201301
+4.6,-422.1957924
+4.65,-420.585814
+4.7,-405.7099648
+4.75,-376.705374
+4.8,-332.8442755
+4.85,-273.5517711
+4.9,-198.4235188
+4.95,-107.243248
+5,0
+5.05,123.0950114
+5.1,261.5920289
+5.15,414.7869835
+5.2,581.7064469
+5.25,761.0934252
+5.3,951.3941194
+5.35,1150.745782
+5.4,1356.965802
+5.45,1567.542157
+5.5,1779.625372
+5.55,1990.022128
+5.6,2195.190674
+5.65,2391.238193
+5.7,2573.920275
+5.75,2738.642665
+5.8,2880.465438
+5.85,2994.109794
+5.9,3073.967611
+5.95,3114.113962
+6,3108.322765
+6.05,3050.085745
+6.1,2932.634905
+6.15,2748.968698
+6.2,2491.882084
+6.25,2154.000689
+6.3,1727.819262
+6.35,1205.744629
+6.4,580.1433756
+6.45,-156.6055438
+6.5,-1012.053042
+6.55,-1993.616758
+6.6,-3108.51231
+6.65,-4363.678717
+6.7,-5765.697746
+6.75,-7320.706946
|
