diff options
| author | Christian Kolset <christian.kolset@gmail.com> | 2025-04-24 17:39:37 -0600 |
|---|---|---|
| committer | Christian Kolset <christian.kolset@gmail.com> | 2025-04-24 17:39:37 -0600 |
| commit | 2d2b7b9f5731dc5c7bda29c917a6cc5f17b5160e (patch) | |
| tree | b566dc6e44f9e63abc94a18f6697010ea981ab89 /tutorials/module_1 | |
| parent | e53c35223bed9a32f1e9cd3fe75caf344d4b5c7e (diff) | |
Updated markdown formatting for latex conversion.
Diffstat (limited to 'tutorials/module_1')
| -rw-r--r-- | tutorials/module_1/array.md | 34 | ||||
| -rw-r--r-- | tutorials/module_1/arrays.ipynb | 100 | ||||
| -rw-r--r-- | tutorials/module_1/basics_of_python.ipynb | 128 | ||||
| -rw-r--r-- | tutorials/module_1/basics_of_python.md | 12 | ||||
| -rw-r--r-- | tutorials/module_1/classes_and_objects.md | 4 | ||||
| -rw-r--r-- | tutorials/module_1/control_structures.md | 3 | ||||
| -rw-r--r-- | tutorials/module_1/functions.md | 2 | ||||
| -rw-r--r-- | tutorials/module_1/fundamatals_of_programming.ipynb | 6 | ||||
| -rw-r--r-- | tutorials/module_1/installing_anaconda.md | 2 | ||||
| -rw-r--r-- | tutorials/module_1/intro_to_anaconda.md | 2 | ||||
| -rw-r--r-- | tutorials/module_1/jupyter_lab_notebook.md | 12 |
11 files changed, 160 insertions, 145 deletions
diff --git a/tutorials/module_1/array.md b/tutorials/module_1/array.md index c8f2452..3385231 100644 --- a/tutorials/module_1/array.md +++ b/tutorials/module_1/array.md @@ -19,14 +19,13 @@ A three-dimensional array would be like a set of tables, perhaps stacked as thou If the load on this block changes over time, then we may want to add a 4th dimension i.e. additional sets of 3-D arrays for each time increment. As you can see - the more dimensions we add, the more complicated of a problem we have to solve. It is possible to increase the number of dimensions to the n-th order. This course we will not be going beyond dimensional analysis. ---- -# Numpy - the python's array library +## Numpy - the python's array library In this tutorial we will be introducing arrays and we will be using the numpy library. Arrays, lists, vectors, matrices, sets - You might've heard of them before, they all store data. In programming, an array is a variable that can hold more than one value at a time. We will be using the Numpy python library to create arrays. Since we already have installed Numpy previously, we can start using the package. Before importing our first package, let's as ourselves *what is a package?* A package can be thought of as pre-written python code that we can re-use. This means the for every script that we write in python we need to tell it to use a certain package. We call this importing a package. -## Importing Numpy +### Importing Numpy When using packages in python, we need to let it know what package we will be using. This is called importing. To import numpy we need to declare it a the start of a script as follows: ```python import numpy as np @@ -34,8 +33,7 @@ import numpy as np - `import` - calls for a library to use, in our case it is Numpy. - `as` - gives the library an alias in your script. It's common convention in Python programming to make the code shorter and more readable. We will be using *np* as it's a standard using in many projects. ---- -# Creating arrays +## Creating arrays Now that we have imported the library we can create a one dimensional array or *vector* with three elements. ```python x = np.array([1,2,3]) @@ -52,9 +50,9 @@ matrix = np.array([[1,2,3], *Note: for every array we nest, we get a new dimension in our data structure.* -## Numpy array creation functions +### Numpy array creation functions Numpy comes with some built-in function that we can use to create arrays quickly. Here are a couple of functions that are commonly used in python. -### np.arange +#### np.arange The `np.arange()` function returns an array with evenly spaced values within a specified range. It is similar to the built-in `range()` function in Python but returns a Numpy array instead of a list. The parameters for this function are the start value (inclusive), the stop value (exclusive), and the step size. If the step size is not provided, it defaults to 1. ```python @@ -64,7 +62,7 @@ array([0. , 1., 2., 3. ]) In this example, `np.arange(4)` generates an array starting from 0 and ending before 4, with a step size of 1. -### np.linspace +#### np.linspace The `np.linspace()` function returns an array of evenly spaced values over a specified range. Unlike `np.arange()`, which uses a step size to define the spacing between elements, `np.linspace()` uses the number of values you want to generate and calculates the spacing automatically. It accepts three parameters: the start value, the stop value, and the number of samples. ```python @@ -81,14 +79,14 @@ x = np.linspace(0,100,101) y = np.sin(x) ``` -### Other useful functions +#### Other useful functions - `np.zeros()` - `np.ones()` - `np.eye()` -## Working with Arrays +### Working with Arrays Now that we have been introduced to some ways to create arrays using the Numpy functions let's start using them. -### Indexing +#### Indexing Indexing in Python allows you to access specific elements within an array based on their position. This means you can directly retrieve and manipulate individual items as needed. Python uses **zero-based indexing**, meaning the first element is at position **0** rather than **1**. This approach is common in many programming languages. For example, in a list with five elements, the first element is at index `0`, followed by elements at indices `1`, `2`, `3`, and `4`. @@ -102,22 +100,22 @@ thrust_lbf = np.array(0.603355, 2.019083, 2.808092, 4.054973, 1.136618, 0.943668 ``` Due to the nature of zero-based indexing. If we want to call the value `4.054973` that will be the 3rd index. -### Operations on arrays +#### Operations on arrays - Arithmetic operations (`+`, `-`, `*`, `/`, `**`) - `np.add()`, `np.subtract()`, `np.multiply()`, `np.divide()` - `np.dot()` for dot product - `np.matmul()` for matrix multiplication - `np.linalg.inv()`, `np.linalg.det()` for linear algebra -#### Statistics +##### Statistics - `np.mean()`, `np.median()`, `np.std()`, `np.var()` - `np.min()`, `np.max()`, `np.argmin()`, `np.argmax()` - Summation along axes: `np.sum(arr, axis=0)` -#### Combining arrays +##### Combining arrays - Concatenation: `np.concatenate((arr1, arr2), axis=0)` - Stacking: `np.vstack()`, `np.hstack()` - Splitting: `np.split()` -# Exercise +## Exercise Let's solve a statics problem given the following problem A simply supported bridge of length L=20L = 20L=20 m is subjected to three point loads: @@ -128,7 +126,7 @@ A simply supported bridge of length L=20L = 20L=20 m is subjected to three point The bridge is supported by two reaction forces at points AAA (left support) and BBB (right support). We assume the bridge is in static equilibrium, meaning the sum of forces and sum of moments about any point must be zero. -#### Equilibrium Equations: +##### Equilibrium Equations: 1. **Sum of Forces in the Vertical Direction**: $RA+RB−P1−P2−P3=0R_A + R_B - P_1 - P_2 - P_3 = 0RA+RB−P1−P2−P3=0$ @@ -137,12 +135,12 @@ The bridge is supported by two reaction forces at points AAA (left support) and 3. **Sum of Moments About Point B**: $20RA−15P3−10P2−5P1=020 R_A - 15 P_3 - 10 P_2 - 5 P_1 = 020RA−15P3−10P2−5P1=0$ -#### System of Equations: +##### System of Equations: {RA+RB−10−15−20=05(10)+10(15)+15(20)−20RB=020RA−5(10)−10(15)−15(20)=0\begin{cases} R_A + R_B - 10 - 15 - 20 = 0 \\ 5(10) + 10(15) + 15(20) - 20 R_B = 0 \\ 20 R_A - 5(10) - 10(15) - 15(20) = 0 \end{cases}⎩ -## Solution +### Solution ```python import numpy as np diff --git a/tutorials/module_1/arrays.ipynb b/tutorials/module_1/arrays.ipynb index efb14bb..7fe777d 100644 --- a/tutorials/module_1/arrays.ipynb +++ b/tutorials/module_1/arrays.ipynb @@ -22,11 +22,12 @@ "A three-dimensional array would be like a set of tables, perhaps stacked as though they were printed on separate pages. If we visualize the position of each element as a position in space. Then we can represent the value of the element as a property. In other words, if we were to analyze the stress concentration of an aluminum block, the property would be stress.\n", "\n", "- From [Numpy documentation](https://numpy.org/doc/2.2/user/absolute_beginners.html)\n", - "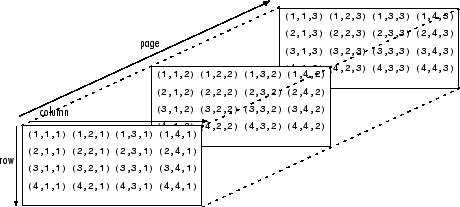\n", + "\n", "\n", "If the load on this block changes over time, then we may want to add a 4th dimension i.e. additional sets of 3-D arrays for each time increment. As you can see - the more dimensions we add, the more complicated of a problem we have to solve. It is possible to increase the number of dimensions to the n-th order. This course we will not be going beyond dimensional analysis.\n", "\n", "---\n", + "\n", "# Numpy - the python's array library\n", "\n", "In this tutorial we will be introducing arrays and we will be using the numpy library. Arrays, lists, vectors, matrices, sets - You might've heard of them before, they all store data. In programming, an array is a variable that can hold more than one value at a time. We will be using the Numpy python library to create arrays. Since we already have installed Numpy previously, we can start using the package.\n", @@ -42,6 +43,7 @@ "- `as` - gives the library an alias in your script. It's common convention in Python programming to make the code shorter and more readable. We will be using *np* as it's a standard using in many projects.\n", "\n", "---\n", + "\n", "# Creating arrays\n", "Now that we have imported the library we can create a one dimensional array or *vector* with three elements.\n", "```python\n", @@ -78,12 +80,13 @@ "metadata": {}, "source": [ "# Practice Problem\n", + "\n", "Problem statement" ] }, { "cell_type": "code", - "execution_count": 4, + "execution_count": 1, "id": "7f2bcfe9-6e3d-424d-a08f-520682b3bdb5", "metadata": {}, "outputs": [ @@ -113,6 +116,7 @@ "source": [ "## Numpy array creation functions\n", "Numpy comes with some built-in function that we can use to create arrays quickly. Here are a couple of functions that are commonly used in python.\n", + "\n", "### np.arange\n", "The `np.arange()` function returns an array with evenly spaced values within a specified range. It is similar to the built-in `range()` function in Python but returns a Numpy array instead of a list. The parameters for this function are the start value (inclusive), the stop value (exclusive), and the step size. If the step size is not provided, it defaults to 1.\n", "\n", @@ -158,7 +162,7 @@ }, { "cell_type": "code", - "execution_count": 6, + "execution_count": 2, "id": "0c5de840-6256-4de2-9845-1c80a12c062d", "metadata": {}, "outputs": [ @@ -182,6 +186,7 @@ "source": [ "## Working with Arrays\n", "Now that we have been introduced to some ways to create arrays using the Numpy functions let's start using them.\n", + "\n", "### Indexing\n", "Indexing in Python allows you to access specific elements within an array based on their position. This means you can directly retrieve and manipulate individual items as needed.\n", "\n", @@ -196,16 +201,19 @@ "```\n", "\n", "Due to the nature of zero-based indexing. If we want to call the value `4.054973` that will be the 3rd index. \n", + "\n", "### Operations on arrays\n", "- Arithmetic operations (`+`, `-`, `*`, `/`, `**`)\n", "- `np.add()`, `np.subtract()`, `np.multiply()`, `np.divide()`\n", "- `np.dot()` for dot product\n", "- `np.matmul()` for matrix multiplication\n", "- `np.linalg.inv()`, `np.linalg.det()` for linear algebra\n", + " \n", "#### Statistics\n", "- `np.mean()`, `np.median()`, `np.std()`, `np.var()`\n", "- `np.min()`, `np.max()`, `np.argmin()`, `np.argmax()`\n", "- Summation along axes: `np.sum(arr, axis=0)`\n", + "\n", "#### Combining arrays\n", "- Concatenation: `np.concatenate((arr1, arr2), axis=0)`\n", "- Stacking: `np.vstack()`, `np.hstack()`\n", @@ -215,24 +223,7 @@ }, { "cell_type": "markdown", - "id": "b1194250-2861-4001-899c-ced19f0f34ee", - "metadata": {}, - "source": [ - "## Practice problem\n", - "Problem statement here" - ] - }, - { - "cell_type": "code", - "execution_count": null, - "id": "777186e0-f734-4bc4-93f0-6746b428f821", - "metadata": {}, - "outputs": [], - "source": [] - }, - { - "cell_type": "markdown", - "id": "29f020bf-b714-49a7-96bf-4e20138c7722", + "id": "e7d2add3-0806-49a0-9b85-4b23e96eca7e", "metadata": {}, "source": [ "# Exercise\n", @@ -240,28 +231,55 @@ "\n", "A simply supported bridge of length L=20L = 20L=20 m is subjected to three point loads:\n", "\n", - "- $P1=10P_1 = 10P1=10 kN$ at $x=5x = 5x=5 m$\n", - "- $P2=15P_2 = 15P2=15 kN$ at $x=10x = 10x=10 m$\n", - "- $P3=20P_3 = 20P3=20 kN$ at $x=15x = 15x=15 m$\n", + "- $P1=1010 kN$ at $x=5m$\n", + "- $P2=15 kN$ at $x=10m$\n", + "- $P3=20 kN$ at $x=15m$\n", "\n", "The bridge is supported by two reaction forces at points AAA (left support) and BBB (right support). We assume the bridge is in static equilibrium, meaning the sum of forces and sum of moments about any point must be zero.\n", "\n", "#### Equilibrium Equations:\n", "\n", "1. **Sum of Forces in the Vertical Direction**:\n", - " $RA+RB−P1−P2−P3=0R_A + R_B - P_1 - P_2 - P_3 = 0RA+RB−P1−P2−P3=0$\n", - "2. **Sum of Moments About Point A**:\n", - " $5P1+10P2+15P3−20RB=05 P_1 + 10 P_2 + 15 P_3 - 20 R_B = 05P1+10P2+15P3−20RB=0$\n", - "3. **Sum of Moments About Point B**:\n", - " $20RA−15P3−10P2−5P1=020 R_A - 15 P_3 - 10 P_2 - 5 P_1 = 020RA−15P3−10P2−5P1=0$\n", "\n", - "#### System of Equations:\n", + " $R_A + R_B - P_1 - P_2 - P_3 = 0$\n", + " \n", + "3. **Sum of Moments About Point A**:\n", "\n", - "{RA+RB−10−15−20=05(10)+10(15)+15(20)−20RB=020RA−5(10)−10(15)−15(20)=0\\begin{cases} R_A + R_B - 10 - 15 - 20 = 0 \\\\ 5(10) + 10(15) + 15(20) - 20 R_B = 0 \\\\ 20 R_A - 5(10) - 10(15) - 15(20) = 0 \\end{cases}⎩\n", + " $5 P_1 + 10 P_2 + 15 P_3 - 20 R_B = 0$\n", + " \n", + "5. **Sum of Moments About Point B**:\n", "\n", + " $20 R_A - 15 P_3 - 10 P_2 - 5 P_1 = 0$\n", "\n", - "## Solution\n", - "```python\n", + "\n", + "#### System of Equations:\n", + "\\begin{cases} R_A + R_B - 10 - 15 - 20 = 0 \\\\ 5(10) + 10(15) + 15(20) - 20 R_B = 0 \\\\ 20 R_A - 5(10) - 10(15) - 15(20) = 0 \\end{cases}" + ] + }, + { + "cell_type": "markdown", + "id": "54b896f0-97be-4ffb-b654-bb5108f99374", + "metadata": {}, + "source": [ + "### Solution" + ] + }, + { + "cell_type": "code", + "execution_count": 3, + "id": "fc0244f6-d7f2-499a-a929-7f080d981b3e", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "Reaction force at A (R_A): 25.11 kN\n", + "Reaction force at B (R_B): -24.89 kN\n" + ] + } + ], + "source": [ "import numpy as np\n", "\n", "# Define the coefficient matrix A\n", @@ -279,21 +297,13 @@ "])\n", "\n", "# Solve the system of equations Ax = b\n", - "x = np.linalg.lstsq(A, b, rcond=None)[0] # Using least squares to handle potential overdetermination\n", + "# Using least squares to handle potential overdetermination\n", + "x = np.linalg.lstsq(A, b, rcond=None)[0] \n", "\n", "# Display the results\n", "print(f\"Reaction force at A (R_A): {x[0]:.2f} kN\")\n", - "print(f\"Reaction force at B (R_B): {x[1]:.2f} kN\")\n", - "```" + "print(f\"Reaction force at B (R_B): {x[1]:.2f} kN\")" ] - }, - { - "cell_type": "code", - "execution_count": null, - "id": "5c20b2fd-d9ce-49fa-b2d7-259e5b121bc7", - "metadata": {}, - "outputs": [], - "source": [] } ], "metadata": { @@ -312,7 +322,7 @@ "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", - "version": "3.12.9" + "version": "3.13.2" } }, "nbformat": 4, diff --git a/tutorials/module_1/basics_of_python.ipynb b/tutorials/module_1/basics_of_python.ipynb index 1776291..fc98569 100644 --- a/tutorials/module_1/basics_of_python.ipynb +++ b/tutorials/module_1/basics_of_python.ipynb @@ -2,14 +2,6 @@ "cells": [ { "cell_type": "markdown", - "id": "d9cee0e6-c132-44cd-acd4-1208721e2007", - "metadata": {}, - "source": [ - "# " - ] - }, - { - "cell_type": "markdown", "id": "a5c32509-d4c7-4fd5-92cf-1a923b78f443", "metadata": {}, "source": [ @@ -17,12 +9,6 @@ "\n", "This page contains important fundamental concepts used in Python such as syntax, operators, order or precedence and more.\n", "\n", - "[Syntax](1_05_basics_of_python#Syntax)\n", - "[Operators](1_05_basics_of_python#Operators)\n", - "[Order of operation](1_05_basics_of_python#Order%20of%20Operation)\n", - "[Data types](1_05_basics_of_python#data%20types)\n", - "[Variables](1_05_basics_of_python#Variables)\n", - "\n", "---" ] }, @@ -34,8 +20,10 @@ }, "source": [ "## Syntax\n", + "\n", "### Indentations and blocks\n", "In python *indentations* or the space at the start of each line, signifies a block of code. This becomes important when we start working with function and loops. We will talk more about this in the controls structures tutorial. \n", + "\n", "### Comments\n", "Comments can be added to your code using the hash operator (#). Any text behind the comment operator till the end of the line will be rendered as a comment.\n", "If you have an entire block of text or code that needs to be commented out, the triple quotation marks (\"\"\") can be used. Once used all the code after it will be considered a comment until the comment is ended with the triple quotation marks.\n", @@ -53,6 +41,7 @@ "source": [ "## Operators\n", "In python, operators are special symbols or keywords that perform operations on values or variables. This section covers some of the most common operator that you will see in this course.\n", + "\n", "### Arithmetic operators\n", "| Operator | Name |\n", "| --- | --- |\n", @@ -168,21 +157,8 @@ }, { "cell_type": "code", - "execution_count": 1, - "id": "a9bc3bda-e55d-4f5a-813d-8f6316f12c64", - "metadata": {}, - "outputs": [], - "source": [ - "x = 33 # Integer\n", - "y = 3.14 # Float\n", - "name = \"Joe\" # String\n", - "is_valid = True # Boolean" - ] - }, - { - "cell_type": "code", - "execution_count": 2, - "id": "f6af843b-159f-4d10-9c84-abebde7e7bbc", + "execution_count": 19, + "id": "125e385b-27dd-4139-8904-10996b536331", "metadata": {}, "outputs": [ { @@ -194,27 +170,44 @@ } ], "source": [ + "x = 33 # Integer\n", + "y = 3.14 # Float\n", + "name = \"Joe\" # String\n", + "is_valid = True # Boolean\n", + "\n", "print(x**2+3*y)" ] }, { "cell_type": "markdown", - "id": "bcc9a481-2421-4df7-82a8-ee1e76c7f4a1", + "id": "98b37bca-8821-4866-8973-80a3315aba0b", "metadata": {}, "source": [ - "Change the x and y values above, re-run the notebook and see what happens.\n", - "\n", - "You can assign multiple variables at once:\n", + "Change the x and y values above, re-run the cell to see what happens.\n", "\n", - "```python\n", - "a, b, c = 1, 2, 3\n", - "```\n", + "You can assign multiple variables at once or on the same line." + ] + }, + { + "cell_type": "code", + "execution_count": 21, + "id": "6d9e59c3-1f38-444a-b09b-6914dba7233a", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "2 7.3 5.3 2.71828 2.71828 2.71828\n" + ] + } + ], + "source": [ + "a, b, c = 2, 7.3, 5.3\n", "\n", - "Similarly we can assign the same value to multiple variables:\n", + "x = y = z = 2.71828\n", "\n", - "```python\n", - "x = y = z = 100\n", - "```" + "print(a,b,c,x,y,z)" ] }, { @@ -251,7 +244,7 @@ }, { "cell_type": "code", - "execution_count": 3, + "execution_count": 22, "id": "a7e71be9-dd9a-42c9-84e2-cb5f8f8939b1", "metadata": {}, "outputs": [ @@ -271,6 +264,57 @@ "y = \"Hello\"\n", "print(f' Variable y is type: {type(y)}')" ] + }, + { + "cell_type": "markdown", + "id": "fcdca3e3-4386-4515-abbe-13242b55c2d7", + "metadata": {}, + "source": [ + "# Exercise\n", + "\n", + "You're analyzing a cylindrical steel rod under axial load for a design. The goal is to calculate the stress in the rod and determine if it is within safe limits.\n", + "\n", + "Given an applied force of 15,000 N on a rod with the diameter 22 mm and a yield strength of steel 250 MPa.\n", + "\n", + "Hint:\n", + "\n", + "$Stress=\\frac{Force}{Area}$ , $Area=\\frac{π d^2}{4}$" + ] + }, + { + "cell_type": "code", + "execution_count": 15, + "id": "cdcc3fde-b63e-4443-a8a1-b59396d3560e", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "Stress in rod: 39.5 MPa\n", + "The design is SAFE under the given load.\n" + ] + } + ], + "source": [ + "# Given\n", + "force_N = 15000\n", + "D_mm = 22\n", + "sigma_MPa = 250\n", + "\n", + "# Equations\n", + "area = 3.14* D_mm**2 / 4\n", + "stress = force_N / area\n", + "\n", + "# Print output\n", + "print(f\"Stress in rod: {stress:.1f} MPa\")\n", + "\n", + "# Check safety\n", + "if stress < sigma_MPa:\n", + " print(\"The design is SAFE under the given load.\")\n", + "else:\n", + " print(\"The design FAILED. Consider redesigning.\")" + ] } ], "metadata": { @@ -289,7 +333,7 @@ "name": "python", "nbconvert_exporter": "python", "pygments_lexer": "ipython3", - "version": "3.12.9" + "version": "3.13.2" } }, "nbformat": 4, diff --git a/tutorials/module_1/basics_of_python.md b/tutorials/module_1/basics_of_python.md index 48952c6..7654e92 100644 --- a/tutorials/module_1/basics_of_python.md +++ b/tutorials/module_1/basics_of_python.md @@ -2,13 +2,6 @@ This page contains important fundamental concepts used in Python such as syntax, operators, order or precedence and more. -[Syntax](1_05_basics_of_python#Syntax) -[Operators](1_05_basics_of_python#Operators) -[Order of operation](1_05_basics_of_python#Order%20of%20Operation) -[Data types](1_05_basics_of_python#data%20types) -[Variables](1_05_basics_of_python#Variables) - ---- ## Syntax ### Indentations and blocks In python *indentations* or the space at the start of each line, signifies a block of code. This becomes important when we start working with function and loops. We will talk more about this in the controls structures tutorial. @@ -16,7 +9,6 @@ In python *indentations* or the space at the start of each line, signifies a blo Comments can be added to your code using the hash operator (#). Any text behind the comment operator till the end of the line will be rendered as a comment. If you have an entire block of text or code that needs to be commented out, the triple quotation marks (""") can be used. Once used all the code after it will be considered a comment until the comment is ended with the triple quotation marks.f ---- ## Operators In python, operators are special symbols or keywords that perform operations on values or variables. This section covers some of the most common operator that you will see in this course. ### Arithmetic operators @@ -30,7 +22,6 @@ In python, operators are special symbols or keywords that perform operations on | ** | Exponentiation | | // | Floor division | - ### Comparison operators Used in conditional statements such as `if` statements or `while` loops. Note that in the computer world a double equal sign (`==`) means *is equal to*, where as the single equal sign assigns the variable or defines the variable to be something. @@ -56,7 +47,6 @@ Used in conditional statements such as `if` statements or `while` loops. Note th | is | Returns True if both variables are the same object | | is not | Returns True if both variables are not the same object | ---- ## Order of Operation Similarly to the order or precedence in mathematics, different computer languages have their own set of rules. Here is a comprehensive table of the order of operation that python follows. @@ -76,7 +66,6 @@ Similarly to the order or precedence in mathematics, different computer language | `and` | AND | | `or` | OR | ---- ## Data types Data types are different ways a computer stores data. Other data types use fewer bits than others allowing you to better utilize your computer memory. This is important for engineers because The most common data types that an engineer encounters in python are numeric types. @@ -96,7 +85,6 @@ The comprehensive table below show all built-in data types available in python. | Binary | bytes, bytearray, memoryview | | None | NoneType | ---- ## Variables A **variable** in Python is a name that stores a value, allowing you to use and manipulate data efficiently. diff --git a/tutorials/module_1/classes_and_objects.md b/tutorials/module_1/classes_and_objects.md index ec85633..3b30746 100644 --- a/tutorials/module_1/classes_and_objects.md +++ b/tutorials/module_1/classes_and_objects.md @@ -6,7 +6,6 @@ - B. Why use OOP? (vs. procedural) - C. Real-world analogies (e.g., modeling components like pumps, motors, or vehicles) ---- ## 2. Core OOP Concepts - A. **Classes and Objects** - Definitions @@ -24,21 +23,18 @@ - Method overriding - Flexibility in interfaces ---- ## 3. Python OOP Syntax and Examples - A. Define a simple class (e.g., `Spring`) - B. Instantiate objects and use methods - C. Show `__init__`, `__str__`, custom methods - D. Add a derived class (e.g., `DampedSpring` inherits from `Spring`) ---- ## 4. Engineering Applications of OOP - A. Modeling a mechanical system using classes - Example: Mass-Spring-Damper system - B. Creating reusable components (e.g., `Material`, `Beam`, `Force`) - C. Organizing simulation code with OOP ---- ## 5. Hands-On Coding Activity - A. Write a class for a basic physical component (e.g., `Motor`) - B. Add behavior (e.g., `calculate_torque`) diff --git a/tutorials/module_1/control_structures.md b/tutorials/module_1/control_structures.md index 15e97eb..f71bd7e 100644 --- a/tutorials/module_1/control_structures.md +++ b/tutorials/module_1/control_structures.md @@ -57,7 +57,6 @@ if 0 <= score <= 100: ``` ---- ## Loops in Python @@ -102,8 +101,6 @@ while i < 6: i += 1 ``` ---- - ## Loop Control Statements Python provides special statements to control the behavior of loops. These can be used to break out of a loop, skip certain iterations, or simply include a placeholder for future code. diff --git a/tutorials/module_1/functions.md b/tutorials/module_1/functions.md index 8235fe3..54c956d 100644 --- a/tutorials/module_1/functions.md +++ b/tutorials/module_1/functions.md @@ -52,7 +52,7 @@ In case you want to return multiple output variable from a single function we wi ## Summary ```python -def function_name(argument1, argument2, argument3) +def function_name(argument1, argument2, argument3): output1 = argument1 * argument2 - argument3 output2 = argument2 + argument3 return output1, output2 diff --git a/tutorials/module_1/fundamatals_of_programming.ipynb b/tutorials/module_1/fundamatals_of_programming.ipynb deleted file mode 100644 index 363fcab..0000000 --- a/tutorials/module_1/fundamatals_of_programming.ipynb +++ /dev/null @@ -1,6 +0,0 @@ -{ - "cells": [], - "metadata": {}, - "nbformat": 4, - "nbformat_minor": 5 -} diff --git a/tutorials/module_1/installing_anaconda.md b/tutorials/module_1/installing_anaconda.md index baa4d71..c6a434d 100644 --- a/tutorials/module_1/installing_anaconda.md +++ b/tutorials/module_1/installing_anaconda.md @@ -7,7 +7,7 @@ This tutorial will cover the steps on how to install Anaconda. ### What is Anaconda? Anaconda Distribution is a popular open-source Python distribution specifically designed for scientific computing, data science, machine learning, and artificial intelligence applications. It simplifies the set up and use of Python for data science, machine learning, and scientific computing. It comes with all the important tools you need, like NumPy, Pandas, and JupyterLab, so you don’t have to install everything separately. The Conda package manager helps you install and update software without worrying about breaking other programs. It also lets you create separate environments, so different projects don’t interfere with each other. Additionally, Anaconda includes programs like JupyterLab for interactive coding, and Spyer a MATLAB-like IDE. ---- + ## Instructions 1. Find the latest version of Navigator from the official Anaconda Inc. website: [Download Anaconda](https://www.anaconda.com/download) diff --git a/tutorials/module_1/intro_to_anaconda.md b/tutorials/module_1/intro_to_anaconda.md index 84c6516..cbd9dd2 100644 --- a/tutorials/module_1/intro_to_anaconda.md +++ b/tutorials/module_1/intro_to_anaconda.md @@ -11,7 +11,7 @@ To better understand how Navigator works and interacts with the anaconda ecosyst  As you schematic indicated, Navigator is a tool in the Anaconda toolbox that allows the user to select and configure python environments and libraries. Let's see how we can do this. ---- + ## Getting Started Note to windows 10 users: Some installation instances do not allow users to search the start menu for *Navigator*, instead, you'll have to find the program under the *Anaconda (anaconda3)* folder. Expand the folder and click on *Anaconda Navigator* to launch the program. diff --git a/tutorials/module_1/jupyter_lab_notebook.md b/tutorials/module_1/jupyter_lab_notebook.md index 5fa493a..14d9236 100644 --- a/tutorials/module_1/jupyter_lab_notebook.md +++ b/tutorials/module_1/jupyter_lab_notebook.md @@ -6,7 +6,6 @@ Jupyter Notebooks are often used for data science and scientific computing such *Note on the difference between Notebook and Lab: Jupyter Notebook offers a simplified, lightweight notebook authoring experience, where as, JupyterLab offers a feature-rich, tabbed multi-notebook editing environment with additional tools like a customizable interface layout and system console* ---- ## Setup and Installation Installing with Conda using CLI: - `conda install jupyter` @@ -19,8 +18,6 @@ Jupyter can also be installed using a Anaconda Navigator - Tabs and file browser - Kernel and terminals ---- - ## Notebook Basics - Creating a new notebook (`.ipynb`) - Types of cells: @@ -32,8 +29,6 @@ Jupyter can also be installed using a Anaconda Navigator - Restarting the kernel - Saving and auto-checkpoints ---- - ## Writing and Running Code - Python syntax: - `print("Hello, world!")` @@ -44,8 +39,6 @@ Jupyter can also be installed using a Anaconda Navigator - `import pandas as pd` - `import matplotlib.pyplot as plt` ---- - ## Using Markdown - Headers: `#`, `##`, `###` - Bullet lists: `- item` @@ -57,8 +50,6 @@ Jupyter can also be installed using a Anaconda Navigator - Embedding links and images - ---- ## Interactive Widgets (optional) Install `ipywidgets` from your package manager @@ -75,7 +66,6 @@ interact(lambda x: x**2, x=5) ``` ---- ## Productivity Tips Here are some keyboard shortcuts to improve your productivity when writing in notebooks. @@ -90,8 +80,6 @@ Here are some keyboard shortcuts to improve your productivity when writing in no Splitting and merging cells Auto-save behavior ---- - ## Exporting and Sharing - File > Download As: - Notebook (`.ipynb`) |
