diff options
| author | Christian Kolset <christian.kolset@gmail.com> | 2025-05-09 09:53:20 -0600 |
|---|---|---|
| committer | Christian Kolset <christian.kolset@gmail.com> | 2025-05-09 09:53:20 -0600 |
| commit | 0d4e770dc06763d225dce66f82bd49b052bead06 (patch) | |
| tree | 3b4e9fa683c89f8eafb8a7454fc191d9e8739a34 | |
| parent | 3eb4be2a880eed828c983c8a30d73faa8e6f4746 (diff) | |
Added auto-generated (md converted) notebooks to modules. Added module 3 tutorials
20 files changed, 1870 insertions, 0 deletions
diff --git a/tutorials/module_1/notebook_1/1_excel_to_python.ipynb b/tutorials/module_1/notebook_1/1_excel_to_python.ipynb new file mode 100644 index 0000000..98d8a02 --- /dev/null +++ b/tutorials/module_1/notebook_1/1_excel_to_python.ipynb @@ -0,0 +1,99 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Excel to Python\n", + "\n", + "- Importing\n", + "- Plotting\n", + "- Statistical analysis\n", + "\n", + "## **How Excel Translates to Python**\n", + "\n", + "Here’s how common Excel functionalities map to Python:\n", + "\n", + "| **Excel Feature** | **Python Equivalent** |\n", + "|----------------------|--------------------------------------------------|\n", + "| Formulas (SUM, AVERAGE) | `numpy`, `pandas` (`df.sum()`, `df.mean()`) |\n", + "| Sorting & Filtering | `pandas.sort_values()`, `df[df['col'] > value]` |\n", + "| Conditional Formatting | `matplotlib` for highlighting |\n", + "| Pivot Tables | `pandas.pivot_table()` |\n", + "| Charts & Graphs | `matplotlib`, `seaborn`, `plotly` |\n", + "| Regression Analysis | `scipy.stats.linregress`, `sklearn.linear_model` |\n", + "| Solver/Optimization | `scipy.optimize` |\n", + "| VBA Macros | Python scripting with `openpyxl`, `pandas`, or `xlwings` |\n", + "\n", + "## Statistical functions\n", + "\n", + "#### SUM\n", + "\n", + "Built-in:\n", + "\n", + "``` python\n", + "my_array = [1, 2, 3, 4, 5]\n", + "total = sum(my_array)\n", + "print(total) # Output: 15\n", + "```\n", + "\n", + "Numpy:\n", + "\n", + "``` python\n", + "import numpy as np\n", + "\n", + "my_array = np.array([1, 2, 3, 4, 5])\n", + "total = np.sum(my_array)\n", + "print(total) # Output: 15\n", + "```\n", + "\n", + "### Average\n", + "\n", + "Built-in:\n", + "\n", + "``` python\n", + "my_array = [1, 2, 3, 4, 5]\n", + "average = sum(my_array) / len(my_array)\n", + "print(average) # Output: 3.0\n", + "```\n", + "\n", + "Numpy:\n", + "\n", + "``` python\n", + "import numpy as np\n", + "\n", + "my_array = np.array([1, 2, 3, 4, 5])\n", + "average = np.mean(my_array)\n", + "print(average) # Output: 3.0\n", + "```\n", + "\n", + "## Plotting\n", + "\n", + "We can use the package *matplotlib* to plot our graphs in python.\n", + "Matplotlib provides data visualization tools for the Scientific Python\n", + "Ecosystem. You can make very professional looking figures with this\n", + "tool.\n", + "\n", + "Here is a section from the matplotlib documentation page that you can\n", + "run in python.\n", + "\n", + "``` python\n", + "import matplotlib.pyplot as plt\n", + "\n", + "fig, ax = plt.subplots() # Create a figure containing a single Axes.\n", + "ax.plot([1, 2, 3, 4], [1, 4, 2, 3]) # Plot some data on the Axes.\n", + "plt.show() # Show the figure.\n", + "```\n", + "\n", + "Check out the documentation pages for a [simple\n", + "example](https://matplotlib.org/stable/users/explain/quick_start.html#a-simple-example)\n", + "or more information on the types of plots you came create\n", + "[here](https://matplotlib.org/stable/plot_types/index.html)." + ], + "id": "3e04cd8a-c731-494a-bf4f-dfe745a8a487" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_1/notebook_1/array.ipynb b/tutorials/module_1/notebook_1/array.ipynb new file mode 100644 index 0000000..f087b7e --- /dev/null +++ b/tutorials/module_1/notebook_1/array.ipynb @@ -0,0 +1,251 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Arrays\n", + "\n", + "In computer programming, an array is a structure for storing and\n", + "retrieving data. We often talk about an array as if it were a grid in\n", + "space, with each cell storing one element of the data. For instance, if\n", + "each element of the data were a number, we might visualize a\n", + "“one-dimensional” array like a list:\n", + "\n", + "| 1 | 5 | 2 | 0 |\n", + "|-----|-----|-----|-----|\n", + "\n", + "A two-dimensional array would be like a table:\n", + "\n", + "| 1 | 5 | 2 | 0 |\n", + "|-----|-----|-----|-----|\n", + "| 8 | 3 | 6 | 1 |\n", + "| 1 | 7 | 2 | 9 |\n", + "\n", + "A three-dimensional array would be like a set of tables, perhaps stacked\n", + "as though they were printed on separate pages. If we visualize the\n", + "position of each element as a position in space. Then we can represent\n", + "the value of the element as a property. In other words, if we were to\n", + "analyze the stress concentration of an aluminum block, the property\n", + "would be stress.\n", + "\n", + "- From [Numpy\n", + " documentation](https://numpy.org/doc/2.2/user/absolute_beginners.html)\n", + "\n", + "<figure>\n", + "<img src=\"attachment:figures/multi-dimensional-array.png\"\n", + "alt=\"Mathworks 3-D array\" />\n", + "<figcaption aria-hidden=\"true\">Mathworks 3-D array</figcaption>\n", + "</figure>\n", + "\n", + "If the load on this block changes over time, then we may want to add a\n", + "4th dimension i.e. additional sets of 3-D arrays for each time\n", + "increment. As you can see - the more dimensions we add, the more\n", + "complicated of a problem we have to solve. It is possible to increase\n", + "the number of dimensions to the n-th order. This course we will not be\n", + "going beyond dimensional analysis.\n", + "\n", + "## Numpy - the python’s array library\n", + "\n", + "In this tutorial we will be introducing arrays and we will be using the\n", + "numpy library. Arrays, lists, vectors, matrices, sets - You might’ve\n", + "heard of them before, they all store data. In programming, an array is a\n", + "variable that can hold more than one value at a time. We will be using\n", + "the Numpy python library to create arrays. Since we already have\n", + "installed Numpy previously, we can start using the package.\n", + "\n", + "Before importing our first package, let’s as ourselves *what is a\n", + "package?* A package can be thought of as pre-written python code that we\n", + "can re-use. This means the for every script that we write in python we\n", + "need to tell it to use a certain package. We call this importing a\n", + "package.\n", + "\n", + "### Importing Numpy\n", + "\n", + "When using packages in python, we need to let it know what package we\n", + "will be using. This is called importing. To import numpy we need to\n", + "declare it a the start of a script as follows:\n", + "\n", + "``` python\n", + "import numpy as np\n", + "```\n", + "\n", + "- `import` - calls for a library to use, in our case it is Numpy.\n", + "- `as` - gives the library an alias in your script. It’s common\n", + " convention in Python programming to make the code shorter and more\n", + " readable. We will be using *np* as it’s a standard using in many\n", + " projects.\n", + "\n", + "## Creating arrays\n", + "\n", + "Now that we have imported the library we can create a one dimensional\n", + "array or *vector* with three elements.\n", + "\n", + "``` python\n", + "x = np.array([1,2,3])\n", + "```\n", + "\n", + "To create a *matrix* we can nest the arrays to create a two dimensional\n", + "array. This is done as follows.\n", + "\n", + "``` python\n", + "matrix = np.array([[1,2,3],\n", + " [4,5,6],\n", + " [7,8,9]])\n", + "```\n", + "\n", + "*Note: for every array we nest, we get a new dimension in our data\n", + "structure.*\n", + "\n", + "### Numpy array creation functions\n", + "\n", + "Numpy comes with some built-in function that we can use to create arrays\n", + "quickly. Here are a couple of functions that are commonly used in\n", + "python. \\#### np.arange The `np.arange()` function returns an array with\n", + "evenly spaced values within a specified range. It is similar to the\n", + "built-in `range()` function in Python but returns a Numpy array instead\n", + "of a list. The parameters for this function are the start value\n", + "(inclusive), the stop value (exclusive), and the step size. If the step\n", + "size is not provided, it defaults to 1.\n", + "\n", + "``` python\n", + ">>> np.arange(4)\n", + "array([0. , 1., 2., 3. ])\n", + "```\n", + "\n", + "In this example, `np.arange(4)` generates an array starting from 0 and\n", + "ending before 4, with a step size of 1.\n", + "\n", + "#### np.linspace\n", + "\n", + "The `np.linspace()` function returns an array of evenly spaced values\n", + "over a specified range. Unlike `np.arange()`, which uses a step size to\n", + "define the spacing between elements, `np.linspace()` uses the number of\n", + "values you want to generate and calculates the spacing automatically. It\n", + "accepts three parameters: the start value, the stop value, and the\n", + "number of samples.\n", + "\n", + "``` python\n", + ">>> np.linspace(1., 4., 6)\n", + "array([1. , 1.6, 2.2, 2.8, 3.4, 4. ])\n", + "```\n", + "\n", + "In this example, `np.linspace(1., 4., 6)` generates 6 evenly spaced\n", + "values between 1. and 4., including both endpoints.\n", + "\n", + "Try this and see what happens:\n", + "\n", + "``` python\n", + "x = np.linspace(0,100,101)\n", + "y = np.sin(x)\n", + "```\n", + "\n", + "#### Other useful functions\n", + "\n", + "- `np.zeros()`\n", + "- `np.ones()`\n", + "- `np.eye()`\n", + "\n", + "### Working with Arrays\n", + "\n", + "Now that we have been introduced to some ways to create arrays using the\n", + "Numpy functions let’s start using them. \\#### Indexing Indexing in\n", + "Python allows you to access specific elements within an array based on\n", + "their position. This means you can directly retrieve and manipulate\n", + "individual items as needed.\n", + "\n", + "Python uses **zero-based indexing**, meaning the first element is at\n", + "position **0** rather than **1**. This approach is common in many\n", + "programming languages. For example, in a list with five elements, the\n", + "first element is at index `0`, followed by elements at indices `1`, `2`,\n", + "`3`, and `4`.\n", + "\n", + "Here’s an example of data from a rocket test stand where thrust was\n", + "recorded as a function of time.\n", + "\n", + "``` python\n", + "thrust_lbf = np.array(0.603355, 2.019083, 2.808092, 4.054973, 1.136618, 0.943668)\n", + "\n", + "print(thrust_lbs[3])\n", + "```\n", + "\n", + "Due to the nature of zero-based indexing. If we want to call the value\n", + "`4.054973` that will be the 3rd index. \\#### Operations on arrays -\n", + "Arithmetic operations (`+`, `-`, `*`, `/`, `**`) - `np.add()`,\n", + "`np.subtract()`, `np.multiply()`, `np.divide()` - `np.dot()` for dot\n", + "product - `np.matmul()` for matrix multiplication - `np.linalg.inv()`,\n", + "`np.linalg.det()` for linear algebra \\##### Statistics - `np.mean()`,\n", + "`np.median()`, `np.std()`, `np.var()` - `np.min()`, `np.max()`,\n", + "`np.argmin()`, `np.argmax()` - Summation along axes:\n", + "`np.sum(arr, axis=0)`\n", + "\n", + "## Exercise\n", + "\n", + "Let’s solve a statics problem given the following problem\n", + "\n", + "A simply supported bridge of length L = 20 m is subjected to three point\n", + "loads:\n", + "\n", + "- $P_1 = 10 kN$ at $x = 5 m$\n", + "- $P_2 = 15 kN$ at $x = 10 m$\n", + "- $P_3 = 20 kN$ at $x = 15 m$\n", + "\n", + "The bridge is supported by two reaction forces at points AAA (left\n", + "support) and BBB (right support). We assume the bridge is in static\n", + "equilibrium, meaning the sum of forces and sum of moments about any\n", + "point must be zero.\n", + "\n", + "##### Equilibrium Equations:\n", + "\n", + "1. **Sum of Forces in the Vertical Direction**:\n", + " $R_A + R_B - P_1 - P_2 - P_3 = 0$\n", + "2. **Sum of Moments About Point A**:\n", + " $5 P_1 + 10 P_2 + 15 P_3 - 20 R_B = 0$\n", + "3. **Sum of Moments About Point B**:\n", + " $20 R_A - 15 P_3 - 10 P_2 - 5 P_1 = 0$\n", + "\n", + "##### System of Equations:\n", + "\n", + "$$\n", + "\\begin{cases} R_A + R_B - 10 - 15 - 20 = 0 \\\\ 5(10) + 10(15) + 15(20) - 20 R_B = 0 \\\\ 20 R_A - 5(10) - 10(15) - 15(20) = 0 \\end{cases}\n", + "$$\n", + "\n", + "### Solution\n", + "\n", + "``` python\n", + "import numpy as np\n", + "\n", + "# Define the coefficient matrix A\n", + "A = np.array([\n", + " [1, 1],\n", + " [0, -20],\n", + " [20, 0]\n", + "])\n", + "\n", + "# Define the right-hand side vector b\n", + "b = np.array([\n", + " 45,\n", + " 5*10 + 10*15 + 15*20,\n", + " 5*10 + 10*15 + 15*20\n", + "])\n", + "\n", + "# Solve the system of equations Ax = b\n", + "x = np.linalg.lstsq(A, b, rcond=None)[0] # Using least squares to handle potential overdetermination\n", + "\n", + "# Display the results\n", + "print(f\"Reaction force at A (R_A): {x[0]:.2f} kN\")\n", + "print(f\"Reaction force at B (R_B): {x[1]:.2f} kN\")\n", + "```" + ], + "attachments": { + "figures/multi-dimensional-array.png": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAcwAAADPBAMAAACKFvyvAAAAMFBMVEX///8AAAB3d3fd3d2ZmZlE\nREQREREiIiLu7u5mZma7u7szMzPMzMxVVVWqqqqIiIigNNJfAAAMa0lEQVR42u1dv48cSRWu2mXH\nu17b92pty8ePYPZwgnQrYSS4hGAiYk+GQKA9S0cAyR5CiNB3gSMCrPsLSCw2BF8A2RHABCTOQRwB\n6CSEhM4ZGV1VXVWvfsxMd3VVV832tqzZqTc9nvmqX1e97+v6pgmpYmPk6m+UsYnAhGnAvD6YVwYl\nUJgCygkMt+i0pGwKKMW8kmmDelA2OPOdGDVlbDaYBGo5lizb0eQdWBAm9c6YtDCfoQ6EKlAyA/ND\nQk758z3+6hF7vD8nIira5PRERr/BG4dzvVfz+Pw+saLkOTFRqAElRTAfkgPRWvKX9/bPm4CIijZ5\n/IGM7i3434XZi5D5t4gVvSlgMhmFajK2hfkLlbvi9eWCvENkVO5/JqP7F82fG0/NXoQc3CNW9PiR\n+BgZheIoUaFHJToE89aFbEHb/su8jYLZXbSbbUWs6Gv536zMm8uelxtgPmnScYZg7n+XtNFzBIi3\nyaxJWit6yosCFS0Ccx3v4t/wb/zPgYB1AJ89WJBLIqO8/UbzziVpojd/1QRvf2L2Wt55/2cERZe8\nL++DikJFKAXMf/InN8/N40fEjr7gD0dfbx7uLNZHX5iXeBSKonSKMA5zjz85XuhHOaGg6Mf8QUwd\nZL4++rF5qcyEYhXrkKs8cDoQqsnYxDChKEyE0p85r0rpbhUFLNvR9DsQiqHMmLSs6NEMFOtXMGnX\nlD6pYbKyMLdlbCKY4U8ZDSYuCiD/hIJo9ZgwrdJnE8yGQLN5gFYLQu3RatVuCTTvQBUtQas3lD4O\nzIZWH0KAVgtC7dFq1Za0WnSgikpaPR+TVne8FNTS6r1XIVp9FqTVZ5hWiw5UUUGrFdmGkVFuBCyp\n4q3fhWi1JNQurdZti1aL6Oi02tUpt8D85tMArZaE2qXVpk1m/FNw9JRn8Hi0usNEYtPqzxn4tJoT\nap9Wy6ik1UzTarmXYOej0eqtpc+VoNUYJe0CM45Ws7K0ukfGDikPtnYgjIWSQkaYZUt3a4jNBrNL\nB6aCeePJzffgxW9v/fwfvYuCoTDZiDDpn4//DT/89e1vX8Sj3IGkpZQSAIpOxohFBfXDnFH6FO42\nD8FiPdvR7NqByc7NRzfehp/+8fir57EZGwdz7KP55AtfhO8s77y76KaH7Oq5yR9+QwNFAct2NLd0\n4LNcMJcnEaWPpx5IMcBVD57f99QDNpdR76K83DezetCnWA+pB1IMcNUDzqh89UBEvYvyIppZPYg8\nL5F6IMQAVz04uGerB0zoBDLqXpQX0bzqQXTGalrdigGOesBlAKQW8E+hpI16F+VXudWDLjrlFphC\nDHDVAyEDeOqBjLoX5WU0p3rQSafcoh589mDhqwdcBtDqAYNWJ5BR96I8f5pVPRi4mLujetB0YFH1\nYOiS9d24KN9Vp9xpWh1b+vSEGdeBkAXlkFJqG8yyNW18UbBDSYtRxq+43gozugOhmoztADO+AyEx\nSgqZz81yMPvqlHEwB3UgpEWZJGmfhV47DHbg4TlZG01Lq3EZmwDmhy0fdmn1EXi0uiHQRxCi1XLf\npLTaKtbzbeQSQrT6EkK0WkST0mpLp8zpCnoJNq2WBPolhGi1iCak1c5Ekg8mvDEHi1ZLAt1GHVot\no+lotVv6ZJwQ9kTauLRaRl1aLaPJaLVXrCeFqQdR/ilfiVnrnoZW+6VPu3wJ9Ei5x+aW00eubGqG\ny4ArSEWVrUgNrfu8A++tJ9CZaTUufSxX0FIOC/zx4BAsp49c2dQMlwFXkIoqW5EeWrmCeVKKVlvF\nOlgCJJgZee+V7f+RK5vOSMAVpKLKViSGS8rOhII5dEKIfX+w9GkFSAOTr2QC80K7sokPlzgqR0oV\nbYcyOVzSL8/NbuPDDOuUHky+kukcARIrm8RwiaNipNTRFqYZWmfFYK7RKVtXELSuoCVfyWSNiU2b\nLPlwaY2JQrHUUWEr4iMl0PsielkK5ibz09CFSvI/4FHKviSiHxWCiRW8TQJk1Jgo/wMUFbV7AZjr\ndcqU5UFaV1Dv93ulTx6YrCzMjaoPzXUwx4bpFuu7ouVANMqANlOv+QmSZWw6mIEOHBPm1nVbVyJp\nt+uUKWBSVhZmB52yXvMTi8nYESYUR4IdrgwmOi+NeiCtS656IKKeeoDMTzyK3VNaPUhQ7FFIlrFa\nPZA2J1c9EFFPPUDmp+ap6EDlnrLUAyAjbNsmEgxT25xc9eAsqB6chdQDsZcWZoeqB51X824sfTz1\nQGqprnogop56gMxPRj0Qexlhdqh6EIGyg/lJaqmueiCjrnqAzE/7/FOkeiD2SqsepMtYpR5IQ5Or\nHsioqx5o3dVSD8ReRpgdpB6w/ihpT/PTQPUAr3+CzOdlN3/pUPWAsszqQZKJZHB5sLUD42BCf5Rd\nZtjKSveug0rf9ZSVmZ8gR8bGwuzUgTDKebl7rqCo0icfzFyuoI7FupVK+cxPbGTzU3zpMwhmHvNT\n1y/fuVgfi1ZDjjNBooRejNTQaunpcWm1iNq0uvkU5AoyF+VlOyWt3nQsISoFlf/HpdUiatFqemK5\ngsxFedmOpdV99RDovbJT0urW/+PQahl1aTVyBSFaLdqRtJr1LdYhyvwErdPHuyi/smg1Y64rCF2U\n5+10tHo9yhWs7hEAmP1k+Wr2Xj+Y0tPj0moZNbSad6DlCkIX5UU7ilZ3HkjksfyU/H3VfBOgH/wS\n6KNeMFv/j0urZdSl1dL/49JqsZwphlZ3ngbbjAUi3ODAfeE9Fhx2pdUsE63uW/rcJW9y43sMzA60\nuhnYxr4oHz7mfyAnKwJvxsAsVrpHFOsv2INmCDqd54CZizp2Freg/3v6w2S5YI63lTM/sZhTNCfM\nLOdmzFemkB4mG9iBO5K0TJyS8R0Iifsgn8kiW9LGDGps+NEMOX0YHL4L27iz3p4NpNUjJK3y/7i0\n+oiRwNVq5ApCa92FUSYfrWYJYD5s+bBLqy+BBK5WI1eQodXSD9SJVkcNsTnNTy8hRKuRK8jQaukH\n6kSr+w9qkPEMoEyyZPdqNXYFGVr92qx1T0+rs8JsXUHu1WrkCkK0+pSPnR1odVTdmBXmJzFr3bfR\nalbd0VysJ9tZr1bnh4nnPTpfT7YjaTUbBFPft0nd/ing8VJR5eZS+rMyzloeL/E1aYJjEKdTroGp\n3Vzq9k8Bj5eKKjeX1p/b36NCHi/+9GEOmAOTVvu21A2DQh4vsN1cWn9Wv2ZtPF786TvJYVIYClNP\nUhSfsLbHS0VB7aX0Z/V7VGjeo+pfQpiUZYB5ThyPl462uxv9eYZgynmPP50lP5owOGmVm0vPXdYM\n97n69Wo8wxn9Wd0kimo9mu9wWeG5OXg9lqdH82hCmENvpdmecENnOE+PTjyhMEgCs5jkN2rS1g2T\nwRRgprjF7XXS1gETJgGTTQPmLiRtPXcRz0qrB3dTYpj6vk0urUbmJ0OrZdul1Zb5KUkVRFMfTW1z\ncmk1Mj8hWi3aHq025qdUtJokhqkNTR6tPgvRatH2aDUyPyWg1QzSw9SGJpdWI/OTodVt26HV2PyU\ngFYzkgNma35yaDUyPyFaLdoerUbmp1S0OjVMZXNyabW0Obm0umkHaLXeKwGtZnlgVkaraSaYldLq\n5DArKvYoTAEmTTqT/OjW+4sfv/WvCo9m0q9z9/Z/Lj79wVt1M5QEyUoJ/O+v36sMZvIhFuhT+NP3\nf18ZTJb6u8Dx2xc3vvb4yidtMwTd/u+8JpgMMsKthlanL31CtLq9+ZFDq5H5ydBq/avNFq22zE91\nVkHa5uTSamR+MrRa/2qzRauR+SmCVrMxYGpDk0ursfkJbJuTR6uR+ak3rWajwNSGJu9q9SpAq82v\nNmNajc1Pia5Wp4fZsmSHViPzE6LV5lebMa1G5qd6aXXLkh1aLW1OLq3Wv9ps0Wp9T6W+tDptsV4t\nraYw1tG8ptWZq6AxDmUFMNk0juYUkpZNAiadBsxJJC1MAiabBkwok7Sb7ubkbsGbRPker+rOTX3f\nJlc9EFFvrbu6u5OlHlger83F3ohDrKseaNpvqQfI42XUA313J0s9QB6vbeoBhTIwtW/LVQ+wxwts\nN5erHmCPV6K17ulptaH9WD3AHi+jHrwOrnV/3XGtO4OCMA3tx+oB8ngh9eCUf1NPPRDR7erB+Ocl\nVg+qXOu+s+oBKwpzLPWAFYZ5Xbpfw+wFkxaZScaHCddJe0VgUjYJmGwaR3MKScsmAZOWh8mrrwkk\nbX6YUANMmjtp2TRgVoFSwGR1/pDX7mzFM/b/4f8cdYyaKi8AAAAASUVORK5CYII=\n" + } + }, + "id": "06fdd8f8-bc8a-40fd-92c8-758d43e6e2a6" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_1/notebook_1/basics_of_python.ipynb b/tutorials/module_1/notebook_1/basics_of_python.ipynb new file mode 100644 index 0000000..023d3a0 --- /dev/null +++ b/tutorials/module_1/notebook_1/basics_of_python.ipynb @@ -0,0 +1,192 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Basics of Python\n", + "\n", + "This page contains important fundamental concepts used in Python such as\n", + "syntax, operators, order or precedence and more.\n", + "\n", + "## Syntax\n", + "\n", + "### Indentations and blocks\n", + "\n", + "In python *indentations* or the space at the start of each line,\n", + "signifies a block of code. This becomes important when we start working\n", + "with function and loops. We will talk more about this in the controls\n", + "structures tutorial.\n", + "\n", + "### Comments\n", + "\n", + "Comments can be added to your code using the hash operator (#). Any text\n", + "behind the comment operator till the end of the line will be rendered as\n", + "a comment. If you have an entire block of text or code that needs to be\n", + "commented out, the triple quotation marks (“““) can be used. Once used\n", + "all the code after it will be considered a comment until the comment is\n", + "ended with the triple quotation marks.f\n", + "\n", + "## Operators\n", + "\n", + "In python, operators are special symbols or keywords that perform\n", + "operations on values or variables. This section covers some of the most\n", + "common operator that you will see in this course.\n", + "\n", + "### Arithmetic operators\n", + "\n", + "| Operator | Name |\n", + "|----------|----------------|\n", + "| \\+ | Addition |\n", + "| \\- | Subtraction |\n", + "| \\* | Multiplication |\n", + "| / | Division |\n", + "| % | Modulus |\n", + "| \\*\\* | Exponentiation |\n", + "| // | Floor division |\n", + "\n", + "### Comparison operators\n", + "\n", + "Used in conditional statements such as `if` statements or `while` loops.\n", + "Note that in the computer world a double equal sign (`==`) means *is\n", + "equal to*, where as the single equal sign assigns the variable or\n", + "defines the variable to be something.\n", + "\n", + "| Operator | Name |\n", + "|----------|--------------------------|\n", + "| == | Equal |\n", + "| != | Not equal |\n", + "| \\> | Greater than |\n", + "| \\< | Less than |\n", + "| \\>= | Greater than or equal to |\n", + "| \\<= | Less than or equal to |\n", + "\n", + "### Logical operators\n", + "\n", + "| Operator | Descrription |\n", + "|----------|--------------------------------------------------------|\n", + "| and | Returns True if both statemetns are true |\n", + "| or | Returns True if one of the statements is true |\n", + "| not | Reerse the result, returns False if the result is true |\n", + "\n", + "### Identity operators\n", + "\n", + "| Operator | Description |\n", + "|----------|--------------------------------------------------------|\n", + "| is | Returns True if both variables are the same object |\n", + "| is not | Returns True if both variables are not the same object |\n", + "\n", + "## Order of Operation\n", + "\n", + "Similarly to the order or precedence in mathematics, different computer\n", + "languages have their own set of rules. Here is a comprehensive table of\n", + "the order of operation that python follows.\n", + "\n", + "| Operator | Description |\n", + "|-------------------------------------|-----------------------------------|\n", + "| `()` | Parentheses |\n", + "| `**` | Exponentiation |\n", + "| `+x` `-x` `~x` | Unary plus, unary minus, and bitwise NOT |\n", + "| `*` `/` `//` `%` | Multiplication, Division, floor division, and modulus |\n", + "| `+` `-` | Addition and subtraction |\n", + "| `<<` `>>` | Bitwise left and right shifts |\n", + "| & | Bitwise AND |\n", + "| ^ | Bitwise XOR |\n", + "| \\| | Bitwise OR |\n", + "| `==` `!=` `>` `>=` `<` `<=` `is` `is not` `in` `not in` | Comparision, identity and membership operators |\n", + "| `not` | logical NOT |\n", + "| `and` | AND |\n", + "| `or` | OR |\n", + "\n", + "## Data types\n", + "\n", + "Data types are different ways a computer stores data. Other data types\n", + "use fewer bits than others allowing you to better utilize your computer\n", + "memory. This is important for engineers because The most common data\n", + "types that an engineer encounters in python are numeric types. - `int` -\n", + "integer - `float` - a decimal number - `complex` - imaginary number\n", + "\n", + "The comprehensive table below show all built-in data types available in\n", + "python.\n", + "\n", + "| Category | Data Type |\n", + "|----------|------------------------------|\n", + "| Text | int, float, complex |\n", + "| Sequance | list, tuple, range |\n", + "| Mapping | dict |\n", + "| Set | set, frozenset |\n", + "| Boolean | bytes, bytearray, memoryview |\n", + "| Binary | bytes, bytearray, memoryview |\n", + "| None | NoneType |\n", + "\n", + "## Variables\n", + "\n", + "A **variable** in Python is a name that stores a value, allowing you to\n", + "use and manipulate data efficiently.\n", + "\n", + "#### Declaring and Assigning Variables\n", + "\n", + "It is common in low-level computer languages to declare the datatype if\n", + "the variable. In python, the datatype is set whilst you assign it. We\n", + "assign values to variables using a single `=`.\n", + "\n", + "``` python\n", + "x = 10 # Integer\n", + "y = 3.14 # Float\n", + "name = \"Joe\" # String\n", + "is_valid = True # Boolean\n", + "```\n", + "\n", + "You can assign multiple variables at once:\n", + "\n", + "``` python\n", + "a, b, c = 1, 2, 3\n", + "```\n", + "\n", + "Similarly we can assign the same value to multiple variables:\n", + "\n", + "``` python\n", + "x = y = z = 100\n", + "```\n", + "\n", + "##### Rules\n", + "\n", + "- Must start with a letter or `_`\n", + "- Cannot start with a number\n", + "- Can only contain letters, numbers, and `_`\n", + "- Case-sensitive (`Name` and `name` are different)\n", + "\n", + "#### Updating Variables\n", + "\n", + "You can change a variable’s value at any time.\n", + "\n", + "``` python\n", + "x = 5\n", + "x = x + 10 # Now x is 15\n", + "```\n", + "\n", + "Or shorthand:\n", + "\n", + "``` python\n", + "x += 10 # Same as x = x + 10\n", + "```\n", + "\n", + "#### Variable Types & Type Checking\n", + "\n", + "Use `type()` to check a variable’s type.\n", + "\n", + "``` python\n", + "x = 10\n", + "print(type(x)) # Output: <class 'int'>\n", + "\n", + "y = \"Hello\"\n", + "print(type(y)) # Output: <class 'str'>\n", + "```" + ], + "id": "e14d8bfc-8b11-4e2b-aaf1-2b676706e16f" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_1/notebook_1/jupyter_lab_notebook.ipynb b/tutorials/module_1/notebook_1/jupyter_lab_notebook.ipynb new file mode 100644 index 0000000..2c00bd0 --- /dev/null +++ b/tutorials/module_1/notebook_1/jupyter_lab_notebook.ipynb @@ -0,0 +1,138 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "## Introduction\n", + "\n", + "Jupyter Notebooks are often used for data science and scientific\n", + "computing such as machine learning as the interactive design allow you\n", + "to experiment easily with your code. For our purpose, we will use\n", + "Notebooks as it’s a useful tool to learn how to code as well as writing\n", + "reports.\n", + "\n", + "*Note on the difference between Notebook and Lab: Jupyter Notebook\n", + "offers a simplified, lightweight notebook authoring experience, where\n", + "as, JupyterLab offers a feature-rich, tabbed multi-notebook editing\n", + "environment with additional tools like a customizable interface layout\n", + "and system console*\n", + "\n", + "## Setup and Installation\n", + "\n", + "Jupyter Notebooks can be installed either from the Anaconda Navigator\n", + "home page or directly from your Conda terminal.\n", + "\n", + "Terminal: `conda install conda-forge::jupyterlab`\n", + "\n", + "## Notebook Basics\n", + "\n", + "Jupyter Notebooks are files which allows you to combine *Code* and\n", + "*Markdown* cells in one single document. The code cells, allow you to\n", + "interactively run python code and print and plot data in your document.\n", + "If you wish to update or change data your code you can re-run the cell\n", + "to update the output. The markdown cells allows you to write text,\n", + "titles and insert images in your documentation using the markup language\n", + "*Markdown*.\n", + "\n", + "To start a new notebook select `File > New > Notebook` or right click\n", + "the file browser and select `New notebook`, this will prompt you to\n", + "select a kernel (the Jupyter notebook “engine”). For now, just select\n", + "the default Kernel 3. This will start a new fresh kernel for us to use.\n", + "Next, it’s recommended to rename the file.\n", + "\n", + "Now that we have a blank notebook we can start to add cells. Add a cell\n", + "and change the type to Markdown. Add a title with the hash symbol (`#`).\n", + "As shown below.\n", + "\n", + "``` markdown\n", + "# Title here\n", + "```\n", + "\n", + "Press `Shift + Enter` to run the cell. You just entered created your\n", + "first markdown cell. Now let’s do the same but instead select code as\n", + "the cell type, we’re going to add some python code to the document.\n", + "\n", + "``` python\n", + "x = 4\n", + "y = 3\n", + "\n", + "x**2+2*y\n", + "```\n", + "\n", + "Again, run the cell and see what happens. You should’ve gotten an output\n", + "of `22`. You can now use the notebook as a calculator, but there is so\n", + "much more we can do.\n", + "\n", + "The order of running code matters. Think of the code cells as code\n", + "snippets. Every time you run a cell variable will be updated. This means\n", + "that the current state of all variables, functions, and imports depends\n", + "on the history of what cells have been executed and in what order. In\n", + "other words, if you run a later cell before running an earlier one that\n", + "defines a variable or function it needs, you will get an error. If you\n", + "change a variable in one cell and rerun it, that new value immediately\n", + "affects the results of any cells that use that variable afterward — but\n", + "not any previously run results unless you rerun them too. Variables and\n", + "imports persist in memory between cells, but only based on the current\n", + "session state — if you restart the kernel, you lose all previous\n", + "definitions unless you re-run the necessary cells. Therefore, let’s\n", + "press the `Restart the kernel` button on the top window.3\n", + "\n", + "Because of this, it’s best practice to; Run cells in order, restart the\n", + "kernel and run all cells (`Kernel -> Restart & Run All`) to make sure\n", + "everything works cleanly and predictably and lastly, initialize\n", + "important variables or imports in early cells, so they are always\n", + "defined before they are needed.\n", + "\n", + "## Making your document look good with Markdown\n", + "\n", + "Creating titles or headers is done with the hash symbol. The number of\n", + "hashes determines whether it’s a sub-title `#`, `##`, `###`\n", + "\n", + "### Lists\n", + "\n", + "There are two types of list in - Bullet lists: `- item` - Numbered\n", + "lists: `1. item` \\### Style - Emphasis: *italic*, **bold**, `monospace`\n", + "\n", + "### Mathematical Equation\n", + "\n", + "Markdown supports LaTeX format equations. Inline equation is opened and\n", + "closed with a single `$`. For a block math a double `$$` is used instead\n", + "of single.\n", + "\n", + "- Inline: This equation is inline `$E = mc^2$` in with the markdown\n", + " text.\n", + "- Block: Whilst this is a block:\n", + " `$$\\int_0^\\infty e^{-x^2} dx = \\frac{\\sqrt{\\pi}}{2}$$`\n", + "\n", + "### Links and images\n", + "\n", + "You can insert links to a different local file or online urls like this:\n", + "\\[Link\\](file.md). I insert an image it’s the same however start with an\n", + "exclamation mark `!` like this: \\\n", + "\n", + "## Exporting and Sharing\n", + "\n", + "To export your notebook go to\n", + "\n", + "`File` \\> `Download As`\n", + "\n", + "You can then select these options.\n", + "\n", + "- Notebook (`.ipynb`)\n", + "- HTML\n", + "- PDF (requires LaTeX)\n", + "- Markdown\n", + "\n", + "For homework assignments, download an HTML version of your document,\n", + "then from your browser, save or print as a PDF. Alternatively, you can\n", + "install the LaTeX typesetting system and export your document directly\n", + "as PDF from jupyter." + ], + "id": "0a5caa39-8f07-4d57-ad69-dc7470ed07ac" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_2/notebook_2/documentation.ipynb b/tutorials/module_2/notebook_2/documentation.ipynb new file mode 100644 index 0000000..f0e6a5a --- /dev/null +++ b/tutorials/module_2/notebook_2/documentation.ipynb @@ -0,0 +1,86 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Documentation of your code\n", + "\n", + "Code documentation is essential for maintaining and scaling software\n", + "projects. Whether it’s an open-source project or your own private code.\n", + "It ensures that you can understand, use, troubleshoot and build upon the\n", + "code in the future.\n", + "\n", + "## Keep Detailed and Accurate Notes\n", + "\n", + "Just as a recipe requires clear instructions, your code should be\n", + "accompanied by comprehensive notes. Document your process thoroughly to\n", + "ensure that others (and future you) can follow along without confusion.\n", + "\n", + "When documenting a project, it’s essential to include detailed notes\n", + "that capture not just what the code does, but how it was developed. This\n", + "includes recording libraries used, citing any external code snippets\n", + "along with their sources, and outlining the sequence of steps taken\n", + "throughout the coding process. Such comprehensive documentation enables\n", + "others—and your future self—to understand, recreate, and maintain the\n", + "project more effectively, reducing confusion and improving long-term\n", + "usability.\n", + "\n", + "## Explain Your Decisions\n", + "\n", + "In programming, there are often several valid approaches to solving a\n", + "problem. When documenting your code, it’s important to clarify why you\n", + "chose a particular method—especially if it deviates from common\n", + "practices. Anticipating potential questions and addressing them directly\n", + "in your documentation helps others follow your reasoning and builds\n", + "trust in your solution.\n", + "\n", + "<figure>\n", + "<img src=\"attachment:figures/rubberDuck.png\"\n", + "alt=\"Rubber duck debugging technique\" />\n", + "<figcaption aria-hidden=\"true\">Rubber duck debugging\n", + "technique</figcaption>\n", + "</figure>\n", + "\n", + "A useful strategy for articulating these decisions is the “rubber duck”\n", + "technique—explaining your code as if you’re teaching it to someone else.\n", + "Whether spoken aloud or written down, this practice helps you clarify\n", + "your logic and communicate the reasoning behind your choices, providing\n", + "valuable context for future collaborators or reviewers.\n", + "\n", + "## Include a README\n", + "\n", + "A README file serves as the introduction to your project. It should be\n", + "placed in the top-level directory and provide essential information. A\n", + "good readme file may include: - Project title and description -\n", + "Installation instructions - Usage examples - Contribution guidelines (if\n", + "applicable) - License information (if applicable)\n", + "\n", + "This file acts as a roadmap for anyone interacting with your project. \n", + "\n", + "## In-line Comments\n", + "\n", + "While external documentation is vital, in-code comments provide\n", + "immediate context. Use them to explain complex logic or important\n", + "sections within your code.Here are some guidelines to follow: Keep\n", + "comments concise and relevant. Avoid stating the obvious; focus on the\n", + "“why” rather than the “what.”.\n", + "\n", + "## Maintain and Update Documentation\n", + "\n", + "Similarly to your code, the documentation should evolve alongside your\n", + "code. Regularly review and update it to reflect changes, ensuring\n", + "accuracy and relevance." + ], + "attachments": { + "figures/rubberDuck.png": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAPoAAAD6CAIAAAAHjs1qAAAACXBIWXMAAAs2AAALNgG/CNh6AAAA\nEXRFWHRUaXRsZQBQREYgQ3JlYXRvckFevCgAAAATdEVYdEF1dGhvcgBQREYgVG9vbHMgQUcbz3cw\nAAAALXpUWHREZXNjcmlwdGlvbgAACJnLKCkpsNLXLy8v1ytISdMtyc/PKdZLzs8FAG6fCPGXryy4\nAAGINUlEQVR42pS9B5RkyXWe+Ux6b8r7at/TvsdPjwXGYoCBB40oaVe7okTRSaR4KLcSjw4piTK7\neyjqgBJXEgmRIGEkAgRIAAM3GO9n2sy07+oub9N7895+NyIrK6u6hxITgzrVWZnvxYu4cc1//3vD\nvPexX3Vd13FaoVCoVCoFg0F389VstwzD8Pl8tm231Yt/+q0WL4/HajQaHo+Hz1eqJd7hM41GXX+m\n1W7U6/K7ZVnNVqFarfMLP8OhSCaT8Xi2XZBLeX0e7hIM+rlaONjP74FAwOv1murFXWybr1dN12ip\nF1fjTb7OXcyAl5HwsVq1HopElxZXksn0rl17Xnv1dS62d/9Bvri8vGrbnsHBwYMHD77+xluFQiEe\nj5fLZa7AF9Pp9Pr6On/lmj714hfeN9TLtX3yc/PF7/yJAeib8lKz5+i/yp/arqVe+gr8ibvwJx6Z\nkfMOf+Ln5rN7Wq3y1r16Xvpj+k1j88XvQQ83M1uGbZhWtdHkDiG/lQh7/+SPf6+UXbKcsm3UvT6r\nWi+HQuFareaYXsvsDJubu47hmhZX4Fnr9UrMY4esxp2H9/6zX/m58tqSxYy6ZT0wBsCAmWHLNVgL\nfpenU0PVj6xfHk+MmZTVsT3+YMA1rFypmimUVtZzX/3TZ4ORYNP02L6Qa3tbbbfRav/4A1NMdX9f\nKsiKez2hoN8y3Faj4fd6LP2wrrX5uDKHbsDeNg9OZzb4k9e2nbbBQjAMppd3+CXcP/gf/ssfPvfW\ne21v1LLshN/84u/828VL7wZNmXyP32ep9eCbTeal1azph4lEIm691Ww267UmN9Vix2M3q02mwHXb\n+XyeO/FOrV7hr8gQS8wX+YqspenoxY5GErFYgjeH+kcXFxfvOPkQbxaLxfHx8VQqFYmE2BuyKk5b\nbxLbDOiLMIO1apVfuLitXsy4vFmraWnQH8tXskpMA81mq7+/38NTGw5jSyaTzBejGhoaYTi25WWN\nc/ni1K49DJu/8lOLXTQaZcG41KZMGHrkHQl23d73tUxrqe2Ke69Q2j2Cq3/Rgqs3if5698P8wgR2\n10//1C8es/eyW0Lv8uAIrWN7vMEgex6l1OQxY7FYfn3e67E9hs9EpI2OpkBlmQYDcESYeN6uKDF+\nw6y0arbtrq6vV5uIs4wtFAyxCh2dgnh7fVoxWZsP3B0tG46dUyjkUZTpZIJ9VK7WWfvBdGJ0dPjR\n0fHVteXvv3AmkfDbhmdyarxQrN6Yn3MNT7XSLBaqbtC1I7avbbJirmO2WB5XjcqS5VYaQ5QOI+xO\ni1YjeiAMUtbIcLV4aA3FOAPhEItrqnVgsDxIpVJhL/C0TJ3HcJqmbHm3WW+ofdbW67E4v6onhd8R\naBQ/osbl2E/cxu/3cz8+wKPyMxD0oSOZcTYJ6xcKBVGfqGr+1Kz7G+o1OjL+/PPPxyKDkUgskYhd\nv359ZTl3ITuzvr4aCPgHh/pZuZWVlWgkxPUbddErfEvrRR4GceR9Rs9Prd314/ltNEQIaS41227T\nDfiCTstdXlxqttxAIJTLFQYHR/KFEnMSjsYtT6BWLRqmXW1wHdFhjUarXGuYHp9lWF0BlV+YIeYL\n+Wi2lLwydTJhstxK/i1ZJiXu/Fv91KJgy+S5WqNrWdfL090nXXHRH9A6Uv/SK/fdTbLju7VaGSFD\nWTaqVcew0BEhn2X7vCPDY3PX3hfLie5vVy3Tg56SuTLkQSz1LAg9w0TiGW69XkWDOy3D6/evZrP5\nciUZTQS8bqte8FkemXZTBoAutNSzNGp1V02CpUZmIyu2TETMjvC45Wql1mhpI8+0uk7r6sXzP/HZ\nT7799hkMRiQcmLn0/tFjJyZH+nLZQq3abDTabn8qFIpgZmyvJbqsWZcnZWvKNlQmiInVBtOy9AaQ\nWWq1teOAEe7sW1upEpvPOkwMMo0gIDumHUBKm7VyvVqRjSRjdz3Xr19juFpxistRK3NFteqyBjKx\nth30+RHliZEBFGEo2sfV+YX3uZwYAdfll+XlZb2uLACvWq2OIuY6i3PF9fVMIpGoVdG+g2trmWq1\nwebhzWQyznWKRXRxvt6oImCi0to1U1sTy/V4XSUJzVa7lUjGDbWzkWy99tqx8XllGIzU6yvZNvbN\ni6BXyrVm26k3WRxPItl/971jbJlavc71g+G4KHVRDBZfMiw+xsbw15V2VxJmmT0vo9nqFbuulu06\nGzsUc8e1EUMn4uGoTcPfuSPjl2+b+qclUyzbw2Yx9VT36nJZwO71ja0XmxZFaNi+ar1he1E61YAf\nQain0/18sN1i5nCfuK3t6AWUm4uCN9U2FXlgaPIhbo5e9Jgeb8toL61nzHS0WsxGwngZAX/AzxOK\ndmPDYCUsO5S0O8bKNbpblBfKi1lFBCNMqMdGK2FqMtlCKt1n+QLPfPzp3/3in4XazvDw8Nzc3MHD\nh4b6k0hGSdyfBXzIeCiUSsQi0eDw4IBIs9vSs+AouRcRr4tiElHWQmHaOLla1vVcd7aBjEdGy+TM\nzs+x9GHbg0vcZPf6PC0XJd1mL3lW1tfC4TB6LpXqS6eTqGRmIBIK9/WlEaOg36t8OJFg8VLYFU1L\n+R4OT8iQeTY8Ab3YuCh8BgWDFPIZxoSOb7q1Jz/64Ugk+rWvfQ1JZQRhKzAze5XPZwpNeUDb8Ye9\nskct0x/yt1tVDHLA78NKWOKamGK+TUNpetnvbYkp2oyFd0Tc7bDPZzLUcLzf6/FH44mAP4QVj8WT\nKA+Mq8cX2Mjk2GB4NYFApKA2IU8j7pArJrReqzeaba6ww4eWyXPatmhxVlwLt6t1e69Xo11Z7a0o\ng9Pqujq9PrcjMmZu3xjy6vjESoGZm56x9rJ6rU13pzExjXoTvxUDGAmEGQXCVituJENhbtto1Q3Z\nYiLGCImsXb0tik/cG711HNMV/RmPxssSdDU3CvmIZbzyxptjA6nrVy8R/4jjaFpdIyNjM8yuUWVd\nWBsVUNnKI7K9PptlDaoXanFoanCaOLBaw3V84qOfOH9j4Y233jWD0YmpqeGJqfXzuDex8bHpvlSS\nHV/M59gd6xsr169dRQ6TqTiakWsh7bWmqLOBZJqp0OLnuE0Gpu7b8TNZJT3BEtAor4ZdPDe/6PGI\n6ea5o+FgNBKpM0zm0zA9H3vm0wwRSfX5vOJKeqxsdiMaCldEB8seLJdLSDu6TK+Ha/lRxlqgtbFG\n3NGpbF8UvA52mSU2A6NHT5Qr2XPvvY1fMTjUh+ezvLRq2e5nPvspLnXt2rWrV6+0nSYDkC0o16y4\nbkivca1ptBsicmxsVi4cjvKgTGssxkrFuHgoGOGfAb944S0VrGQyuY5biQdrmvmSuHettpVIpKLR\nONpnZXU1moizYNg5diODlNijVhOZU3fd9E+IiFztzOin7hXErivS66N333eMzkUsra67LxbQtrpS\nrrYxGsfBmCsngzs6yqB2Al8esPvVrirltb62YXm8gYg/k8lmckVwAqxuX3ogETQT8XSlsIpCwK3H\noUeht/GqlEvCam/uzU5ski9mMSsey0P02ofoJfufePwJv/ej+XyW+axXJGrSIZOK32qoAx0sieTV\n6h35a7VNr4lnggxUKiUdbwRDEWRgctfufQdvcwzzV371H375K//99NmzrmmfPntuytcOBz2JSCgW\nCWKZ+5MR2xrHrZqbnUXW1tbW5mYXuClLjP4NRSIrK2v8VUMIlhVwxZ9FHpvK3UJN6LWQ+WEnIg4z\n8wuFQt3jI6KXEG73/gmn1cSWmRK9WB5cKdsXWVkvEDWWCgW/33vj+jUBLopFj9fyilFuCbjQltiR\nVywhmAbBtg6HFYoS4jYqSPehUHnxJlZVwJZAOJlOhSLhUqmSzxfZgdF4/Oq1G6+9/g5f0UAIDwNG\nwl4MhQKRyEAsmkapM7lciosh5YFQkNupsLnVFN/daLSa6LZKHUNnZ8o1rQhDIV++KlKCAmg7GNlI\n2ylqiVxaXmWnsTPZk0BDlgqJWvXGxuoaYQ26otUWUdMC6+oNY4qTgYQS7ewMXjc1dK/cd2Mpsyee\n690GXf2t8ZkuaBMOBrVvIPG9aGGX+/Ix9IJ504tv9fcNeH2BcCJRLBGAtBpND27MUDpsNgrDwyM3\nKhlXDKyn1qp5XLvFzNheCSkldnU7cYfbcZASsXipkLNca2117cL5i5f37ZkYHbYrmZjXa8fQfR49\ne626WRfPDYgFfxh3MWBvvuRxjC20ikfA2q9vZLOF4sWzb10490402Xf42PGf+T//umt7vvrV/3H+\n4oWA14kGPfGIN+hDXjFEylutNacnRzEUSs21ULO5XG51Za0ycwNrhpCwrBERhiB6SsyLz1cuF7G4\nYniMjkbAoPkD3u/94HstFzgxgA1D+R49erhULvAnG6uGds+Xq9FYu1yph8KRWqPtD4bFWTXtUrlm\nW2puHGBHAaa8nqDrt5EbCUaDke4a41fogBXR4cbIMXGS3hvoe8PnrixfQWqZkGbD4c0D+4/0nRpo\nNtpsKiyXjMxtd7VXtWF3lCEG3XUqZSdXqLXaZQypWGdTxuE4vkarIY6pY7k+3pWnbbjeJqIC5uW0\nUTPNfB7JZnEmx8fZIfhp87NzXoJecZZFqhv16sb6qt/nYQwOV/V6u+CasYlsKGk2d6CBvf56r/Rr\nWdeupJbm3k9q+egNUnVEi//a1d9afWjkd+/evdp50P6D/kUGVK1VqnXbH+zr6wuGo5mMfP369dmx\n/qhEZk2Meytk+xWCHMANrRjis9raG1YPge9uuR0wtOW0cB3YGLVy7aUXXn7TNkb9OUCzyclJ1lT0\nSNvBnQ0HLD1CsUH4FA1Rp53HU/46e5iJYJxhnzc8GB8dTPj8+xZW1lY2Ms89+81AOLZn3/7Pfvyp\npdU73nvu6wMDyVDQ67SxvUALuK42YQ1IiZoskcx4NJaIJVS4YRWKWVyPbDYLjMFDIPL4Qlr02W7M\nCQNRfk5LT+CLL77K98QUBIMEc0cPH0Gvhf0BkxiASC5sG6XsWsRvW+2m3zYblXIqkSS656dPCYEt\nwJBCncSdbbZ9LsLk8XmLxTITmi8U0IPr+bIvGEKjx+PJquuJRqLDw9Pcm3mrsFgePz5wOj2ISdlY\nzzKUYimfiofn5maa+EYGK4jtbYfDcezzYMDkzarj1pk9nG9cYafJghitClcJ2M18tkB4g/rFKIFt\nDcSZdiubKQFJhAz+c9Yyy319CSzujZm3Gf/KyiWcmWBoP3YJaYjGAtxLgfo2AxgdHSyVclgSLPYm\nltIRLK1x643yligLytmJULnUpvjKHhKLX28icAG/BKnqu+KXi11U0RdwmH5HgY+YwRAaKxqOegPD\nDMavXt37djEoLWT1FlqgsxXTsXTNzXkaZjSUuPjeu1NjQ8F2Pbux/MU//8rkaL8lEa63Va8FWfNm\nGXcwgLehAw9LpMrt6HeRs1Ixx0asO61aq1myvOdXs8Av6WjYXFzwvb2ciESAx8eG+0cGUslI0O8z\nUcLtZgV77xHrZ0i0226WHPQogIbHdAUTbdUEssRrcGxfOBg6dnTaF5x568x71+dfffvc9bvvve/B\nJ57BYZ6fu7GBYxkJtGr1ZqOWjEdaKofAbDEZzEyz5XRco6ARiSaHRtPlSruEw1SsrK5nZmZuhNAJ\npjM+NoKj3zIsgQKHJr/7g+dmy14QkEalGmnX7t7V3+9vAdxnc5WQz8v+9hSr9QOThBYhMUO5Qggv\nIiZ+T0A0BLPcYJ0YhUo7yBb3BIIDA9Ps8+GxlF/yQsHh4VFHIV0C0QRClUpN45Ub2UylYRNSsgnJ\nAV25dDkYiMgicjXLKuSy6WSqVi+jMBq1Bh8IByM+j7cIKJ5Ogjvi4rQKK6lwmNjUaBp19gQaKxL3\nR8jkGAQ3hrHKeK4UqpMT0+IZ4wLhUxluuq8PLA4PrJDP79+/b3FxaXx0rNWogySBn9WqFVz2M2fO\nIF488sbGxv79B5lZ7SuLcLY6qQOtpAP+8HZ/3dJKndiBoELMCILutJklLou8Ev9pzAorFwrFwxEB\nOnQ+zuuR9JmOifVdxBXuRA2yEzTY2vWOehNb2nOQSKlSI7rnef3Ar4T0YXZx0Osz2Zb9qfCZc2/V\nO9A6e9GxbO+mjdn54gEFozfkvogZt8ab3Vhbr5ULAa94mJidmZmZYMCTikXi4dDIQLofQH2ovz+Z\n9nktvuG0GiQUvU5DjIaEAOgl8avrTZFaO+7YrGxxo7A6V8uulOut/Maip125EvHs2bV77+5dIGbL\niwuNZjUWSaF3cRjEkiiLWqw0KjXWy0aLVysFQZe8vmDYAo5I9ZnOWKNdr+Uz65bhXLx6FcU+vW//\najmbb/n/4MtfR3wr9fbY8MjK3NWnn3o03j/YKmUDRG5O3WRTZouN5195k2GCCeJpOE6GJRkeGmEq\nEupFqK5fAlOSgGh6MaNXrlzhT4QCYm6qgWw+h85mZn0+waRMtd6mL95AjThZ1gw/p17bUD6PhXi0\nBFppjoyOLSzIDh4eHizkyyg5yZCFI0sbOaNW3DWYzCwtrF49jeztP3KiHY7lKuAOAU8k2qyWCuWN\naiHjMdrBgYlYKk2WUeJ2p43Tl+6L57MZtDgb68qVS6T8Zm/MjA5PbKzn2J+MQeGktUKhhEB2hRvo\nueuP4jJ5VSzLK5svaF3bbDR1fKb1rkriEDxZLElff1qkGVMeDvtDya56VptHgg3t2BB414pOO1tx\nN2NiZiMQMLu4u9Mjm1shbo+zJLvCcX3+oGu0vbaXlGm53ow64WC87+DR22Nhu2V62+KkkyACeNPx\ntntLcVexsr64ZARxGPbt2+OKvm4AO2IjJOlXq+WKNTbYiteeW8bx84ZDgUQ0kk4lBvvTJPVAEMOe\nsjgSpEzFZ7J8PJBPHq1SreAr54v57Oqiz6kHwn7XstNBq29w7MzZ80tLKyePHR8aHq9WStyoVCmB\nzbWV24wdBV3wE4yDL6PgbPFWjabkhgRPJbjG+wVWrtVIzfpCETzdhdWNYDT5+3/4PxY3Wt6E32k2\nKvVaPJUkbChUKrhBHrceCwfY3J7HPvJJZUPdUDCITAOSIPQECnhReMnY/VKlWmg45SJWmFRWkxxE\nfa1Yd/01B/wvLutq+0NxSRIBF9UJxX0BBeB4gpGYSki5QOzBAPCWWa1WcESRANTqyuoCDsry8uLs\n3PX77r0fqWDt4REUTX86FTaLjrdVrSxdx01plKq5eGri6F2wEQqlZiCKVvKQADDr606rksnnVjfW\n+S4oAS4Wylci4CBjsAcGh1ZXlhFHdXFDZwkqtWokkvjMZ36cBRYEIBJHjYVQYjbugqERJ2ZAZxYR\nhXhqiPmRr0Zlq/BSQTYZzSAfIGrnGdkVWje3HDu3XtiedvUxJLwgSeLKlFqWV8epHfkmbdQNZG3b\n7pXyrqbvQpkajweAYIwE+Y5pF8rNQKgeDXpZg3DMZ2DBWgC4wjTAD8PXtm+KmzeVv437xR+BR4Bt\nmA0ShQSv5GD0lmaMtrLnuEayzxs1IOflxQ3LysbjueRi1u+fY9gn9vQF/YFoLAyaFwASxqVhulvt\naF+ab63k5rLFcrnewLBGE1F2yIG9e3ZPTpx+9+0fPfeDu++6c3RocHVlicWShDpqBhfFEkgaJBrf\njulNhvwOmSPXaDjiS2NATJXPGB8ZYpwMONnXH01kyg33/PuXiMSKlUIqEV1fWviJzzy9e3KsUSaT\nEPBJWqyJ6vW0LWyXD1VWI1jIldcyeSw66x0IRUw8EccAEERbCFnGA8Aa8pjt9dxGKp0im89CliqF\nXLElaVuvIZifxwyGgiBKmUKuk79tZ8+dPX/s6O0D/aP4OKRbPJZZq5QG+lJl8s8BXyGbGxroa7eg\nIRRBuOxYQnxikRVHexcoX+Yim8njSYF4Egm0mzXEA9uCzzp6eBcBOKAVY1RMAVkdvy+I/J869QAb\nGCEOeEOLi6vBUIL0R6UhyeBK3VlYWFDkEB+DFKwXlo4HOCiG+tHpYYV8ESo1uqLW+cnUk02ol3Ru\nThyegIZZ5M/BUKCrqiUUVIq+SyVw2j361ZKg2XY8O0gKvUr95uBYLIYYjbaJeoonCd5dyyfarllp\nm55QLFFcK7YVEA3Qg6o03Ftrd50BbSvhRs9rUKVSKsciYcRUvBFJZltA7JYkSr2hWNwOlCx/SMbm\n91dc3DbBBP/shbf9Xl84EgIxTyUEeyAvTl6yTt69aWzU7ZYvbgS9VdNIRlPxwcnCxgoO5LFDB1m1\nH33/2enp6UcefIDfs5kNdpTZbrAKPGU5u1pTgXs1V8XVgfkDvi85RlObX7eQXVE6wlsu5AZSqf/2\n5f8eDQbqwhYx0yGvnQjsnRrLry+b7RqBX7vR9PrRJYZnYGQMlL8JICJ5TEcSXdGwzoEhPQSg0XDI\nsLwkYsBaWVBc5+WVuUYTnLUyOT4x0J8CpzcILwWsbmDCLYMQ1wkS+wa9zbpAlpJkLpfTB5MwJXQg\nyKSsri1imaemJxAtVAt5UPTeyOjQUrZe3KgC4pjD6eTkbQ3ffCReH9x7IJhIgSVtFCvtWslpNKYm\n9xzcvScS9C4XaxpKaYiT1GCRuFoiGUWvE8JfvXYRj4WEbqlYHx2daLfsaBKG0iAyePDw7WwGdDmS\njdXSqWkN87OiaM3aRomFxxT0MqI2xc4RTEDiZfE2eSbJq6vscqFU7OKGCjrgLz6tv8k3bypOUa5e\nhcA4NWfHxXXAqohJbi+LZtPFB45t6PiX8AwkUeJmB3hdoJKRkZGLa7OiKZ0mDg0311y0m1/NdjMa\nRLJxQ+qWGg9pkLWVVUsQ+g5rRRscTRdDHTTU3hBsU3nVLGIykTTbcXzDYrW6vrDmzi4LuKRApMGB\nAcXRaLSDSb8/ju4KJ4ddXxgkczwmBJP04JA/HDl37ty3f/ijEydODI5NrCwv5rKZhMebTPdVy37i\n5ngy3i77CdUMfGty7OLwiMZB3PtjYWQVHwfRiofjo+OTkQvX8ourkMBI6u7dtWt+doHM0eT4kCcW\nwtlqVpFM13N1Zo57Y6ir5XwiEp2emCQZlVldjYVCEodVSx7xMDHWTdvyIPoYcNTz0sI8WpcIZmJi\nokUcXW9g5e2gBJREGawIChUwJ7+aP3xkfP++ffgH/Anlgbhzu8GBvnIp+9bbr73x+ss59vqR40Lk\narlMN+amb7APUHitVneSY2Mje3GRCCk21lfY66S2w8FwsWVWS+2VQkn0dI00hA8iZCAYwfNHAkwx\nAd62Y4XCyXC8cded92IA+9JDSHy91vYERFJBteots7yWg1hSqjhaSXc4SJriYqJl2O9BzcaQfLat\nuQMdfL2hLIzVtiX5Ii66UuQgHv5IB6QX3oCzyZ1pqXwzbhasQYmJ+acOc0MeX69G78XvbwmA+gUe\ndrygEq0GmP3K0hzrIAhdUGBvMMSLZ14FmiOMI39lbTMnO1+b6a+O0cCDHR0dzawt6oS8PFNzK8Ol\n5d72Cp0GLKKY31hbWeCdgE+SO0g/M8/zCSJM1q/RvHZ9TptHj+L2Saqq1VrP5eq55Ugsym2Jc4ZG\nR4xo3+LG2vwPX3n80Q+HByeLjmdmbbXoiNNHdFvKlKKBSBMHqy2BN8OR/YP7TPKaSKpeHxwaaVSa\nr7z7HmqYDXRkfG9fIoW+Gx7pzxfymcLq1bkVD4kwIQAopmc4EkMKSScxbEafy6yG/d54JPzWW28x\n9EQSDApvlZAavdRwmziFrV1TU3M3ZtlV/PThAADcWt5KsU4CgHSyjT1Bpn1BPjB7ff7lV/4sHk95\n7MCh244zIyw/CQKPN4L/89BDD5E0QCPyfrEIY8lmCuAfiy/lWHUCcm9suVCuVYoet9ko5lqVfDVf\nHOwf8vujA8NTkdhYLJ4q5s+SkQaZmpjcBdWOlJ4vKAI0c+MascfIaHB5De8ttbRKVI3XbFXKFQaG\nXmdXkKtK9g+yzKFoHOFj2J1wUHNFmHPSjkbTcXoVcEfjeoRdIUAt49WOCl9kgWvlLdKhgH/iaUpS\nJwDExBqx4ypVrd39nkjIb9YrhS7wos2I5vrpLGY3eO16U8y1UHJIH7gOUSEbRqlhUyiljUZ/OiUZ\n5ZYoZo/FG3AKfLeUdSZeZaNbrG+1WtSkj6eeesp0qogLjo0m1hLUg3nzTx3McDvJX9qWIgWReiTM\nbPAA60yFR4NRIf4v/JFYROVksGaNKiAi26fRnL1+IxAJGhvFtnDwbOPidU32Yjkq33/xU5/4uJ0Y\neO2HL66tLkUCuKzk8i2/Jyg5c1QAO820Gm2AIHL/BsAiOQdgQG8w5g1ENwq1vuGJtfVcK1Ph0yvn\nZvr6E2yNldXFWDiEqgLqkYV76m/8AZfaNb0PgBsPWBFgSFAZP3r++3v2TBNHQrUbG5sQJqgvAJph\niVcGAm68/PLLoOzzcwt3330vCDK6ORgMkToNh/AQGsLOaQr8Um8L4CiuQqNJTCNJJUUiQ+8B+Yi/\nWKmQSC+WS/jiPPbSwnkCmlwme+LY8RszM32pNEI3NbWLaBPXKtE3yHyVa0YJvBYYm51eq3Ovs2fP\nMrkDAwNARo899uG5uQUN8+kgku0k7BqfCIej0kldjpeCFDq0O6E19pACtH5t1ivd/FFHI7ZFc+vf\nGfDC3CwD5inw+JEMj8+/I7HaFdleqnBPDNru0rjlTRWxWF22r/5rz6jauJytZtjvh0IIMPXOu2+z\nPMh9IOwDlzLapf/wb37NaOWiYaNVyxrtessKa9bgdo0uYTmBbNDvhxnvF6fLHh4Z/Ft/62/d1W9p\nj0s9gyjmSr1Rb7QKpRLxYr5YXVpZX8+TnKyD2Ah1oKrYRyo72iKugYbl86rsjxuPJaPhiPxDEV0Q\nd9GxlbxiIogPh0JTfJ62JpwfOnTomU98CmH7h//gHy0ur8SiAv35IwhVfqCvf3V1FTpayB8QjkOt\nEg4EJRQSNledm/uVruWm2Rrp+RAxq4SSEte2VQzV0NbVgwO0b99+4X/XO+Cx0GM83o997GPf+tY3\np3dNIsfz8/PjY1OIJukY2xuH2ABV/e47H37ttdcO7D+KCWMDNMxGJsv7iUxmBQ8Hldk/mCCarRb9\nQdstlfPIerWQvb6ykllbx+ZyL2SFJ5nesxcdSRANZnLgwIGzF8b6030oG4iSu/cc4gNst/VsaWR8\nYnFpzbGD7VzlnTPv+8Kh/QduA+LVmmbP/n2sDgIHFRZEEk5MUIVc2n0EqIESinoQYnUPT6tLIdEw\niMpnu9vpX8SyXs2c3qJ6W5Ks0QKhiCVeTcrXXnIvU/KD0rHuB4SPva/NTeJ2yhw27w5g0FSOu4i+\nCjGZSfaHN0B2UiosYKy7hRwSi8mVYWpixGbGQF9bcq4eH+Z6048X2h1J6NnZ2eBiQcP/bADNCxCA\nQTCTAMo1FvAkdo+b3t3gQ7bA855GtQUMPb+0uLC4DERWLFWaZdhUIvQbgIAWwW4gCIEsEBafGRJY\nOuEI/EAkWGsIJN1QLGUJGkmGYG8/9KEP/dt//Zu//Mt/H9QfPZVbWyHWyqyt9iXicKLKbi5BzjUa\ne//995mTgB/wl8yGl2uBqyD0yYi/UsrXauZAfzo5lMbrY/dFggEytcJYQVD27T+AjaqR8Wg74VhU\n2PZus1KrPfDwQz/44fdAPR955MNshlA0wjyXM9WgN8b04ns+8/THIXUBEFUqBa8NBFVZXy3nC9ml\nxSs8BpLKPov4IuNjk9wvu77Brvjkx57mqQ7uO/jOO++MToyjjA8fPHD+0kUw1DPnzpLVD8UHLl9f\nOLBv//xSdqh/yPWEK21P3+jutWzR9EZqjhdBPnTsdlFyFlkpTH8eP0rycM1mppAPRMLL62sSYfl9\nZP7wN3kaOKxtRaJuqVKZrjT3ip0SU3fHmx2+2JbgdugNwu5wwD1tbUCakqalDMLVUV0vgXHH1W4m\nmd3yT4Yq+9A8A80I6fHvRfuSM0V9adKBpsdJPhJ2aCgqSrGwojie8M495hZ9uLN/9PV7NxW6X3ZO\nC8h4/bG7dtdVYQOiA/uoJVlCS1K+4B41oZ35AiHtB6JlcF7AzL3DMf+JA5iQfKl8Y37h0rWZxZVV\nZL9QLFdr4gLBb6/ki6oQIgIQJTwrv8CB4ruG8PKCqOpEMsbdk/HEyy+9AHfsn/+z/+urX/3q+soq\nUsc+gShGLkglSPCDKCVrXbsyIzQV4mzbq4qzwD+iff2pVBTNPjY6PLR/757hoQEvjAnDBWzNbqwD\nodiBgbsG+gd4GsUqNiSoJ0Ljz9kN0mz33nfPrl270Rrk4ZeWlskL4vUTZa2sLOHwLC0tXLt2ORwO\nfPnLXz516r6FhfknnngSU/BjP/ZjjOrppz92/PjJO+64y+ML1putyalpCB3ZfPHc+YvkAjfyBcLB\ngeGx2aUVfsLtC8aSG7liemgyEkvVG07/4Gg0lmq5nnTfMFNi2RGAt4YjxXGhWAC2DwkBFg2gTHBY\nidmxIRVh/tQbkWhMOPIQ9xGOljAEBblTnzE3RbAj8W2n68xY27lfnXjRdXqYiV2Zd5Wn7ueymkEQ\nVEwvCV5ty9he0NSLM+6gl3X1t7n1V6XOt2TU7eW7a7iHSNBWsA95nywZEuiikZCpVg0I8NKFs7nV\nRcBSMBCMuGPqqhRXUwl6vCwerK2LVrgOnhwinU6lf+zRe1GCOJ2xWBjEOsgWCvqSkTAAhs9yqbTz\n2g5BAWUJVov/6ik/RqRhNCpmqxbxWiP9qUN799518tix2w7umppMx+Pg3LgVgiaxEsQuqPRqGd+V\nV6VSbgjK5EgOr9k6cujQNFIyNfXcD76Xiscefeihhx+8P+Tzv/7KKwtz82+98eby4iKE0JWlFUQR\ntobivUo2tyHuJZkposhIv2Rtpw/u35uORRxgk1KumF3PLM97oYc2qp5nnnkGLLNUksw/vi/instl\nlvCcYqGrV6+ePvMOZoiB3XbwCMbl6JHjoQRRvLFr/4HnnnsO+sD1+asPPHwqlozhWw+PTr319vvp\nvomvff0HU1NT7757DT7alYWc1x+rGoX40HjbF2chP3noCNZuaNdtkYhRKBuBGt5hLTY0CFARDjlV\n2KTV1tBAdHExV61m9+8ZvHhxWcFeETYD2osCrNm5NWI1HCpMEAAyoobA4cloeJtl05Di9tU1emV6\ny+tQyljzI7Yc6N50jDCVNpnuUglkaH0pmTT1XbwdEhWS53KEMeveSnN/kA+jk5rGJve4t7RPO0id\nmoYeoiVpi4ATMIURJXuXh83nc+BhUV+QRccnGRgcnnlPMDfBhXgij6svIyQx2bymfgTF/qFik4ey\nVH5N4Km5uXmd61DBVRP1TjGngaxWK5ADpAKBiaoJ8R1AxpRy4VY1XzCkQEVgAJQ/mS+0GDTMoOEe\nnBrdNz1RrrXyxdLy6trM9dnF5aWF9QwTqRIrlM452fXa6tIyFqC/P332zBlAv/1791Ju8eKPnnca\nTZAiHJ+LFy8SFAH7UjCUL8+3VQliMhJjXtBnkr0mvm824R/PLS2txWwKX1D2w/192JCoouB7TQPS\nCvQve/jgU7Nzc/lCsVAsrQC7wu8MBXbtnn7l1Zduv/Pk2bNnHn3ssWszM+VK9WPPPJPL5SkVevPt\nN6/P3jh+8vjA0OBGJjs7P/+pT//YjbmFQDCc7hvYu39XOArPYCibK1P4FojHCqXKxOSYjLLtYVdA\n3GXoZAQWV0jVeqidiybCa9mqJ+gH/SsXS5CnCoUqkB3AOShh30CUhAW1YaLDPRDHLFLXcE8kpLZd\nijPgpxSLJXQtqkO0uJh7ciiSWVRJXBQw9ASkR6o8SVP11oOpFJ2p05lWjw7eooVtAd+qYE8Xlylf\nXxVWt/iQDhLYYlxVh7s7lPoHq/au/t78p6ml09D1E/pTZk81tISDhqIlSCWXBxcYll4QYmwQXi7f\nRjxq58++DcsQ55Lo0ewUbXbrooReJPc0NVfMkadUhHGpEjWsn3jqfrGB8EsAngV49OiJEDZ5UOKD\nltIloFj8rElVQwASIECVI+srrDHZSDjjksZCrEnrOol4ePeu8aNHDtxx4uie3XvGhwcZVAUVXy5L\nuBwMIZEUqWCcuf7ly1eF5VGGJSj8x32HDmWy+QuXLo1NTVGnhnFIxJOxSGw9lyWmaKmd2RBDLulw\nAZgqtdMXbvzgxTe+8eyP/vTPf/j8C8+9d/HK9fnlvuEx5sJ++if/kUeq9IcPHTrCA546tR8WWn9/\nHNX+wAOnzpw5zTjId/al+xGgjfXMbUfv8Afij3zoyWisLxROHD9x+x13HimW2yNjY5FYjAvCwmaK\nQTWTBBep4CsvvkJEQ6DwJ//9TyxV9VevVWdmrmFJ+CeB/fhEJFdoB4M+aDPwIWJBX6lYAJ40VUEJ\njwex2+f3RqJgW55cntggH4+HW+1aJkORqzfgC7FOALPaGedZpNYGWVcUdgF9CdrkZ5OfUjvlsbrI\njGa0brkuhtnL49UiLvpPCWcP3mLqdzpYjdRQtLo7xOnU1xg7YuKbN8Bf7Mxo0Fp/xO1BQpsCqAsK\nSaAZlD1vgAr4hQfONCPjrUjI+8bLP4KyhealkNcRi+RK8eeWMyO1TcBaQmo0KNfyaIFHa3DDJ+49\nLCx519AV2WquTNnJ7GeYd6qRAaCgIURddkOgWK01hS0j7FlTJcgQPSh/rsZDqH2GzN7kDZRvsdWQ\nithkIkap3vDwUCqVZLGq9RqqVhGrUvD50um+1bUNqvgDyq0YGJ+Y2r2bhKekPGNQxlPEKrVWI5Xq\nFyq4KzWYQjwQpoYlCfu23RSLRUgv1XDZcnNmceP0hZmvPfv8n/z5cx6CcUdiLGgYNbBFMLXrN64d\nOLj3jjvuwLp99rOfHRpKf/3rkuw9cGAqlewjU3Tk6G1ww/L5CgigUaxFogFKnrEgiWT4zJlzMI3e\nefet8fFRwEEs8u7h3aMDqRe+/ywO353Hb3vuuRfuufs++FkhL0hZKxkLbCxX0FKtemsgDZbSLpVL\nwyOJ5aU81DR+x5WKRn0bG6SIJMCCVBONBkvFPMvRl04gbzBOccCCUq4KqVXylDpnpArQBEj3qjyf\no0rOMAego71MrG4eaBsa2CORujnHpvRvVTBp4yA14+0Gy44HSZLbVGH+DiDyLwZnPgio0fRXfUdt\nizpbCFYcvPaGScrdkNBFcFVQBh1Ei9AkUoo3TmkzDx0k1ty+tTarB9UwDV14qkBJxYlow7BFJXn9\nZMTZMA1VHIBAkdD06mJ8ABnMocrjQiXyR0MB1Z+DgKKuxJvgrqYLO6VtRENKTRFoYDduiMDUW0Gx\nGWwtnz8ZFRbN7SFY0MGllVVEkcdcWlqCCYO+f+mVV48cOlw0jU9+8tMPffjRf/kvfjMST4xNT1Lm\nRIy7uroOGQG0QBEimuQKSPyxAetkF4NS3Y+QsPmjgSh8Y3Ag4aRgo+459SB1AqurFODZf/Nnf4pv\n7T+8n/mIJNL1FhbKXliu3f/Q42SYl9bK80sLw6l+pxw7/frL+/fvJ+kTjsWrxVYsGqmgX+vGlXOX\nYnbgxT//IduX5gJDySS5229973noBrg2c4vrRBWUhl+4cml8erJQLg0MDpAVyubrff1Uo0G5sUPh\nKNWkqqDJunRpHkwzmQhlDBp4xHVjAvKzbE7F64CmY4Gs2gGfq1oGgKGj9+ABS44TYoPqRIOoghkj\n9xpOtoXBb7u67lWx27VESmmj4+4oDBXALmj3kFhMlWEVuoWuWgzANgoICUyA1/5+Fli3x9li8EpE\nKMmphhRAqrS8Js90+s+IHlJS5256QVYHPZEwQCyLlEJrpo5uu2EGGmVYLgZVXiTgVMkYpRLtSrlJ\nNZjXI6RFynbL2RvgVk2najnerZI9s8M5o/oXpY6UKOeJoQJZeqRDh+k5PXvtI088ujJ3w2zWx4cG\nUNTgziQK69CEvSGp15YCc7LCjUopR9CZLQnfgbiT2UDIN7WDBBVShSTFbZEhQA+CaKWM0tRtdEyf\npUAGxcLHYuwZNu4/AZkMQPPC1cvAO047tbh6LVOrANeQkfy7v/iz/+bf/Lv11UW+SdhGgdHU9Gir\nNQhcA30LawAwz0ZKy32wNP501CuNXISL4VDl1EmQEQTkhRc+VKlI7mFgwHf+/BL7m+HiRZ06dfAL\nX/jm5z73UQYKvouOB7A8f/68tCRA7cbs9ID/+99/C9FHkuBY8XN6966f/8VfbNQq01ODv/Eb//Yn\n//r/8ch9R6gcr1SOV8v18UceiESswWceR2sUPcbyjevYRMDazIpNQnh9cb1ltoeGhkhPLM4vw4If\nGQq9//4cOH1dWpg0tZalKAmExlDEU8O0b3YVhIjo1UyVzpueTWe93cMm7/7S+XmTn93tf9QbRIqa\nMNwdt+t2gOo2zOiFOLU1MLf3adHxsWWZtwBwXGNHR5reAeuNKpCqqZgtEkJIIKEyr2KOJIjPzepY\nZXsfg7/opXf1hQuXnnz08f6+IYp+Zm/MoYBJk6JHiTgpcMvgdpRK6FEHowEBzqUb1yAAKBHhUF9S\nFRkRVvkUh9S/6Q+qCNvtVKvgohubPU6kTFwZWkc2vQcgHJEcSMfHxx564NR9axtkAjLvXrx+6fw5\nEv5I/C/+/N/5zd/816Db1XIJar4XrFloXaRxIyPDw/hzZL0Ui1BSWzSyaFEAHfRusoakX5gH23H0\n6NGf//l/8vTTT/MkuiQHihjW4Ytf/OORkV9TJWEG1VxsX0kElGt79uxZWlnW/KFMpgVkSX8k9jZT\n/1d/6nPQvVBykOPI2v79X/n7jVors5pvtuovPPej+++/78L582wbLtXfN0gdC7twevfeSF90avfw\nl/74z5/5xEe+/KfP7tk1BUqTSsZfe/XlZuME7GpY0QpJ90iDh3CMn5hF1S7HuwPj603T9JZN39Jh\n6OF86/5VO2W9l5y443ddmd/bBMZU1Wu97Zl6bUXXG+kdjLqC21vO13E2etHSHtBms4hbyhXVNUUz\nAyJXawVxq1otohZEf2R0fO7qaQk8Wsb2rNct8l87/S7He/nKjZX565S5Ld64Jvijx84ViqEI1XRe\n2yeMj1RygvWF+IigO22rt5dOW4wscWOj2qhJrW9PQ7VOvaLb6sq6RqS09FNrZWuwt0ammwfxDtGT\nKBpuG16QmTdfeT4StJ944qlf/Lm//V//6+/zyf5kHFyuTpcvNGupABNRyF2EaA2SxJFEJKzqQn2a\ntYrASG0Gnti+u3/8jjt2U7GEt8Q+ANH8yEc+8uyzz7IHpqcpfupH3KnT0z2SDh2aGBiciBAYx5N4\nY2B02OiHH74NtIrokM2Jn0BjJSLoP/qjPz524vi3vvNsmMTBK6+OTUydOHkCdIVSq5GxcfB72PAn\nb7+DoHtqeldDInrvxUsXd+/eL2nUwaGmVAYJUgAgOzzUn9lYpyCQZAFRFFBwrdpQWRiTbDEOTK9u\nVuLhalRZcQ83m1tsqmpzc/07rHTT3GpdZJg7GIg6sNNr1oXnVb+hzSIjlZySCtJqVXqWbHbGu5ks\noMV9R/+9XtCkF6jZzAAYXQx+SyghObdBmcietFTek6YPZPQKoUjcEtHHVXOatcL5069r+o+1zWa5\n2yXe0RF49w3JTPuMvmR6dmZmKN2XjEXJTU6MT+zZu3f3nn3Y9l3T0+MTY4N9/WHpjSE0MngK8Gvb\nUtdHCWadEMAUsFQKpKTOV2qciN6B1lv6P1Mhu7Zw7gxF7BH+Arq4KR3paCBgQ+Au5XO1UsFrurFA\n8PKNudPvvF1FQxbytKd55KEH9+/bSxwudayuEaSNFmk+kqhum1QmLfhgRBJfAzTi2udodAdGJ2n/\nQCKZCsdi1ElEX3314uHDh4mNPvShEwRIuVzzZ3/2r/ELqSVdiK17u6HPVlerRI3j4wM0oNGNxEhl\nvfCj9/Ds6UsDH2L37t1f+cpXfumXfunOu+8iqXZjdn5s7+Ho4KgnnFgpVCKx9OrsomXV+gbHmdkc\nvs2e/aUGaIPdNO0nP/YM6CQJAiZrZWnh6NG9fXcehfx87dry0SMj584tUKAOS+f8uRvpfvjJC6Oj\nY5UKDcDsXqKsBkZ0z5dNzWJqj1mjjc72qmrzlir/poB1W55V7aVOZwEJ9dxuiwGt4G/JjdHxcbdb\nWC9PYccG2PqraRo3+SKO5egWSaIclSyzyC2VH/R4hB4jGPbgsObWCyfFaP/F2r03Zyz9DAvVu+++\nzzh5wtOq0jISEhsiK70+kVhpRwURvNVUfSyQMEsBu6poq62rt7qzhPndYTc61FB3q1GUKbbKMvRP\nTFFT0hcBjxVKxHS9TjmXOXf6XTaAlJWtrc7NXvsfX/nyJz/5yb541CedvFaFhFOtgCLOzc6rvFXd\nAZIg/RQICk6h+hTxPiwJvS6eBx+8o1gkYyx66v33l8bGhvnEu+9eReXTsgpq4vh44Dd+4z+RjcLt\nYVe8d+EiEw2uHg1bv/Vb/5Ho5MH7T7GPiSdWlpaR+z379r575jRdUKLJ5N2nTiVS/RRRzy0tw3zI\nFkuHjh0p5Eu6+SjjoLcGPRIDEYqJjPmlHAqyRoM7Sg0ymUsXrs1cvyocslrlhR95HnrkkfX14u7p\nXe+/d/7o0UPzN+YHBoLlEkUu24o7e4TS3KGnO79vN+LmNsfG6G372JXO3iKj7u/aFcF062omTS/R\nduDmFqq3Uurm/wqX5mZnpkMHsLQ7gyw72vBCGiGdAvqKvk2l0nC2XcIbgdjbfynfHdiuXKpOjKSX\nZq+EbRHESlXy/wB+4kc5aisKy1OSVihpVkc1XrKgWCrt0nFdYAQoY+jRTq+1yZyWtjqu1cWRFJAr\nF4VU0JQ+WQ0qNHygnKajWtoIsRwSvwZt+pIptPy3vvG1e+65J7eWbVBWa5uDw+n9E0Pdp5jP0uIl\nz06A4w2ZhzoKysiaUozbkJLa118/x0Vh1UnX0qGh3/7t//jggw8SjF6+fBk/HkeNOx05cgRHWXeA\n2H/gAHNKKRAO08/93N95/rkfcu/vPvvtjcza3/6ZT21sGFKx1HYSKYv02bBpkCEaGepXuTlj71Rk\naYHggS5lge985zv33nvvF/7z548ePYbMEP7jIbGLKLHFs7/99hOvvfbKwPDg5Uvnf/Kn/soLL7zA\n3iezQgsDS3rrSV+acgGCXjkUC212mbO0L6CzpJu5//+J725u/723kGIHB70n/WQa7U5soJFp3RVj\nR/+jm8W9F4zvGYSzvR1fx8VS7MieMLqnkVOnqYsyZCZeoJ/Mg8Sp4HtQrwjjaeYDs4heg+Qt/6eR\n6taV1UOnwr4bc7MDqTCSZ/u9dejk9bLXDgoJV+WdZHSOoOpS5teGPOvXo1J1Zy2NOLEr+voGlCtu\nbq8Fo/bUq6tOpauOJXGIHiEsX8VwEvIP7SfYJYFoOOFNHj951/e+/yy0Pxo7U3L05BOPLc7Nv3f6\nXVyaMP0m6E2ZzziS1pVSV24xGUuasfSJiUHDOiqXakkXFlwagEupEvncT/+rL3zhC5ieL37xi/w8\ncOAgkShxKt8E08dEnjx5kgAZUoC0JMArqkh2Y3J6aHh4gFzmsSO3sfzAhfv371lZKSlH2cEF+973\nXj5z9iwQQbNSuHT+8lf++I9Ihf32//07+GWLN2ZKhQx26sDeXSGfZ3Hu+vLCHPDd6OBAKZe59+77\nQUwPHNyPWN92cP+9992HFrj7nqNU3cdjcWacBEUw5CfLgDOMs+dsOuuW0isK9TN0p1iljDs+jL0J\nXbe3t38xe3RbL/Gwp/G02Umeq3Js6UQiV3a0Lm8JvOUAR0jH5+2973qC0a3mM91s1LbN07vlOt60\nFne3l6PWCVUlzwuMyH5rKJ/GDQRD84tL5BVktnFprDYYyUsv/sBp0u6TLnPtD/bd3S6ZQqOl4oQ4\nzYnx0dv27ykXsx4T178lWSjRHobugU7Gk+gQQTLEyXEdJb6uurTUwHilUhjmu0pwOypNZeonkaiZ\nLwj7wdCtexXhTZWmCupKtLppDOjbAemnLjxFM5zkyUtFatDr5GfIH09MjM7QfK5Rp8EGZLIGrR8g\nU0gf4aYkcWtlgz6n9aJTLRhYnmbFbzlhjzuQiA7Eo/b4yU+dvPOORCp54LaD6YH+oZFR6AfTu3cf\nPLRratfYbYen6cFJZRSPkUynaWW2ayDWHw+WC/Q+MKVGmBayIfP6Eiwh+62zNypNK56I8uSXLl39\n3Kcf+/qffKOUX5+eHCeTdvTY0VypPLFrb6Zc3SiU733w4dfeOQ05jA7U9z/08D13Hx0fGx8ZGcOg\nYbwgNYyOjGEZyqX6ymr29JnLmLuFpdXR8VFaggGBtpxGqVby+E16IDJFKBaiFmSOil7USFDqHlpK\nyLTzIjPeUn1QHae9rV21AjocZRxc1fKurf17lUMnQ9tB24UzLix0XFTh30qrZwunWTQZKy7pTCA2\nMm4RVyE2O3pE7hD03t6/hrHDa3e2KJCaw7i9U6TfQyk1/aHpPgXUmqAqs1Ks+uD8VmbDUfwuT9g/\nYLSCaysrc9ff8UUaZkvTcsxOjqnTC9DU23DT8mgFIfWb9IYPRkKPfPiRWqVM/ptJwX+gEh3AiYLR\nmvjGtN9ysR5NKYDx4zCo2ZOLqaC0LUUIbUVk6fSDlb6OQuRXzByDYwDaNLUjK0IPgar0MG6Vac5D\ngOoqp4MqLX7RPUO5UiQGlVuKCHK02sisQy72h6OHjp84f+UKKj+WlJQUPX5rSuhhz2cpVWYj2kKn\nKaNrKyWVB2T1Se5W7F/85/8JV4/8Lb71yAisd4EvkBtImhC5iL7wDFWBr7R95JmuXbn29W98a2hk\niMUGi/3+D16cncu9//57586dh2/5lS/90cnjJ1IJL4W6X/i9P3zkkQdh2vPs9HLJbGTOnDkL5eDO\nOw7ffc8++BHjE5PoYEpDqB94+eW38kVAU28iQSka7Dzft7/9HTqbXL8xs7GROX7iBCluAM41mhoE\ngwuLxBgD2GoBm+lSKH3FZC036bhN3fH0ls6D7iu7o7tdt0J0hyOrVmy7Q9Jxbzqwo6OqQ6RJoCp2\n80vVRevmXNUto96OcrW36fsup8Dc5OtY2/vmiWSpHaq0orgWQHuOUc8WYPVFKRT2WaGAx5dZn79y\n6XXaYputbeScnpEYt/wnjc8H4oE7jh0ym9VEyBvxe6S1neoZLAqAfCg0dzFimiLTomOnIlSqIEM5\nOehdKvUC8ibtytroc/QuiA1F85aUWYgTBgNeAkmBZDwtqbylIYLfY0rbccAzVzBJ6JwoFzebX6cl\nAYTeibFRNqSQIZdXqOPet2/f7Ozc+tqasIVgR3I6Q6MFVC9sNa+P3G4mm61JTSkdxKiHakkXOnjC\na8t5BGh83Le42L6+SH1GH0IUS0W/8Y1vT0/tJjyVCpFsFn/6ySefRLUMjA01jcbc8kL/6KA3aKfS\nkO2Tk1OjeAm7pwdPHvmVerW+tpQbGU78lZ/83PAAPZRHq5LdakaCkV/+u38D5TJzvfyHf/SDxx97\nEsXqC0TWs1mcgX0Hj5ZKhbMXL4ds8J9VTM2Jk0dJxjEf7bauNqB/cWh+YbEvPbi+fh0UlEQg1Xoe\n6X9tbJITha1E6KhTaDfLeu+pGB8EQvf67tqj3Sas2gWyOk3kehsedWiVt7raLYnvH8AY09ff8t13\nXBClaaucrva15XgRu9MFRNoHSBtU2ZKjY2MqIfu/mmMyeioOkVR40apRSnUtuwaMILnbSJQoUk5A\nqDd8ErkalBaBTBU7Je1iGqRYTZ+54ohjr0JpZ8uHUm29PYEkq0NtCC3O2Q7SoE5+2s2KWOO2obYV\n+8D20Syn7aH8XPrVtWrloXQ8dffJ8eGhi1evzVy9DEuBTiHVegsC+aGDBzAG2XI9lB7pi8EXLFoy\nA2nCXO6l+AXNCvVTRMGPfOqXyZn9+q//PwzyxRdf/MhH7qZok6cG3GH3ACwiQ8888/CNG8tHjx5R\n5T3O3afuHBwaAuJHNdEke9/edCoZ9th0ybKoGbPFYaZwy4vc07g+u7FBBxscJEjF2Vzj2Wdf7h8Y\nvP/+45WaalHptXE9W9KLvXnb4b6XXnl/9+TQ8ePHKCjlViTJRkZGB4eGpaVt24HFTlK6vz/q9dHj\nyRsMSfmCan5s9HSR7jRkvDk03BQa92Z0bAdDveesCJzTdu8e6OrdzS6+4pRKQwHd0xQSi+7keFOH\n1FtiMrdqn+r2VOu5XRLb1iBF5ETiTck1SXdXkZiAe2PhGk2CfF64SCFMAG14XnjuTznTwG4bfynt\nLuWM7VYwQOqq3t8/FE+lE/3DrjdUbtuFmltqmQtruUypPru4upLJzy6uZ2vOWr6ylqusF2q5ErU2\nzVK1WagK0Z5Gf1APaM0IHxjHl3bvNAuET0MrBXZAU05PcdThJdLQRvnt8lPcScW8wEiD+9GIzFY9\n+nAiOcCon/Qk7JR0H+1HQdaLwqqk+1CFxs60NgBwnJ25IqWCHi9nWMzOLcwuLMDGWVnNnH3/wvXZ\nOc87b71NGDoxNv7Aqfvxg5799luYCRbvQw8/AhthaCgIL6hYMD77mcevX88A0lPfTEt3llgcANuI\nRX0L83m/N/D+mbN79u6aL+Q5t2RxYe7qldbayhJR7+6JXa+//jqpU2l+Xa70DfTnS0X/emR42Pcf\nPv/Vhx9+eHCwLxLzl5eKMzPVT3/68UaucOnSJcpYjxyZXliSRsrpvn4qI1H55KcUAwymQ5yS9oZ0\n2ZAx0LC6Kz2q+7bdbdZ+MwOxwzG8CRP8IGuw0xUxt5JZkrTa7MWu4wFhUvj821t0dJr/3yz03ez6\nzWCl3lTu9mFsVhvK+QI6Nte1KtJexyvnOOAZm37pWkz8g9GlJ0zLKXj/ktrdDsbzdfvcjZVLM3MX\nry/A9cFiQB2gdxZs0ngirY4wiJRLsuUARipLVVVyLocIUcetQhdDiPINOdTJUm2bKDCF24eJQBfc\nfnia0aZCcQoThMiI9a5LfwEJUE1VHiMNSZVRlWltVXKVsNTd0bWGU43qXtNWp8REQRGptn7nndNr\n6ysYt3dOCy4CSLi6MPPGO6cXF5elb4Xfz6i4Mt+Ynt5NUtD8rW9UdFIAH52edhcubExMpEslHUgZ\nHNLxxhvvsR+g4Jw6tRdeTb7SeuONN2i0eNddd33rW9959JEPc8uHHnqAWliaOs7PXs9mMyS3iARw\nRc68e/rQgUOglsS7MBwIMXk+6lCoaucYLR5M+uaUyjRSlEO2/F74wCMJulsaC0vQlxsb2RzP8KPn\nX7zjrruvXLlGxHz9xizuFlls9hvhibTyo+99ra5xQMrVSDRoIKX3OIDtcuZ+EC5+s9ZXGPM27d4h\nDFubxxC4W1pTdUWtQ3XuavpuIyTV6dPbW9G3xclxmts3WFvfxdYUsU1/YKvfsqRCYSPiENOfgfoB\nGIqGJ9R4+8xLtPFKREaS/iGn1hgZsP/1v/qZzMb54Bb9c7ujZbnbx9P5UN0xMdaPP/LA6uJcqwrw\nmxOyVyCCKwkgTrtSonnEtFYuCb+3XrNDCV0UBk9Ejmdz6OYn/bfIj7qqH6wcFAOG1oGsTKexQqXp\n+OiI0CFTMbqI4cUDsEB/15QKlQqUUZHOkj4/3hg4OvA58kNyVPoiVuX4CXBM8pi0PiejvLi8jD8M\nzwWxfuDUKdQrRaEkgsbHx6Q+kAqPaFQTroTUBeKCYeE/FOfBg+kbN6rkCKamxk+ffl9D8tFoGD/n\nwoUL6pCPBNWt9PgrZPJvvvL6sduOsMDVAk60h8ZbXDqV2kM4E5I2NZV7HnygsFG4/e4jG9IjvwGd\nnT6p47FBmlYODwcF6GgYFC6dOX0NFB9qxIkTx17+3jWcLfh1FP699e47u3btglQMGZiDbhAFShuJ\nPagug6pgFhzKphtV3e8KBls1FKIKHeVqkOSCMtFFfHvFpdtcewe7Syf/b1bw3XTVzbWtSmdb3TOY\ndtAEzB56wi2sxFYaeEetk9m9q+4yuzPYRanSDNOVallHn7ckj2noFlFysEdAZ5Gx+4OZ9Qt/Wd8d\n1k0NEnARTHiDtpccI5cXFDDvlqli8jZa69CciDvJqlM4QFDoqAQz9QkhdSwXGhwmphTR+j1CyVeZ\no03FITOTSu8RZn4ouMGSL9ZylQ36o9Mea6gvRaKAU8Do8ktzRb6IOhOuS6asS8W7Myl7SVlvfHea\n6IYH07cfP4xaVCcgrX//hy8gM1O7ENEF5Ag1rtP/pnjupoc8aLs9+eabbyJkx44d+/znv/uZz3wG\nqjrkCCTg3nuPX7w4+9575/kTPgaJoddfeXV6YpqdHPIHf/u3/uXqSjW2L3j+/JXbbgOtr6f6BozN\ngn5qB/k5Ohk7f355enqoVPGQ5QXNLJab5y+8R/YqGgq9/sarsCDOv3f24YceHBnue+fN1/ui48H+\n8MAgij9ArSBcyPtOPbC2sS4ca2kbNErA6vWLE0E8LgcrmHQ1EZdPUEhh4Vk8NoEHfP1tRx1tvtpt\n55aYSffQmB1tNtrN9i1D2y6LRgvljgh4s4uYfbM3dbPob6/u2wpVdRtJc3sPPbXBOiXim86SOoAy\nGGI2pOgOMFHOqLKp+jH+F1oe7HRm2vAI7VQ8kgdTs0x66FECR1vdXKnCUUMc0MfBArVKJRLySW4f\noCCS0sPTWUhFrCBypeivrb04VXRgdBOrFSfM0nldXwUfnl1VKhjNCs1zFiMb0jdBmtXSlKZJdNRS\nJ3XAqO/rjwSknYm0OYFYjr6m6YgS4irqHDGAfc0YxoYGBtPJ09dWrs3coLPG2OjoirX04ssvMdrp\nqYmJkWHExFMolX2B4OGjR37v937vrnvu3r13FxFFIhV/4623caTeO3+ZCrqBIdp5Re+46xiNLab2\nTeL29I0PsBZUXIST/mKldOz2PbwJOgqDU4oAHHdp7gbPT3a2YUjhyHome/jwQQnpGmRqg5MjY4WN\n7Mc+9uFrl66MDk0EfeFkcvhrX/v2P/7Hv0pPz1JJIlCamNAbtVSAe1TcNUazeU5Nuz4ST5w/f4Zm\nOvBUT9x+u1Avx/e+9OKrTz31+ML8lXBo38BAgkwiscO9d5+Q0J6WEk096cLNkNoyw9Kn6Jk9zo2r\nmv/3bA9DUc07nS40Nq9Vq3Jf5AQxAjr4gUpGWwLU4GYgmh4P8TmeoavP+zQ6nU31kS+6klXVCnXy\nviwn5mrTCnUOTtRIhitOlMejsBJ9UFmHdegQ4fmEsEJa0yXbIblI9Gx/ZGLuwuLQNEDHUr1VXi8E\nDh6//7UX33TsORVyOBoZ6XCHJdPToe/rDqOaQMHdqhzh47Vfev/dr/yX3/t7P/13+pMjsQBtKJzY\nQD+9y+RYLM6mDMDdq7SMMpXFVCILImRKVz1WVzzgtsrHwQSAm4yxUOc6dY1nqVluNXztBrAjrbLx\nV+W0Ajh/fYMDtArds2vfKER+2/G1axNDqUJu3WNa2zVC3WjVIT+yVcCAqrlKrVNXaTaKFT5zZDq9\nuuIuLF1fcisjE5NPf/wTNAQ5f+HStbffB8C1/9rf/X+p0MP3+Mxnng6FoocO7eYgzJGRiV27hpPJ\nAU7tAc0lZcPZeCS0Cgifa2SzJfAmaSm4tvHWm2/iwHz7W99dXNx44fkXAEXnZuc2Mhs/eu45dYBM\naH555dHHPkxPMthdr7766oH9Bzh8LxqNHD68b2Fh41OffIjWIxDn2Y6kb6XDZUO8Y8BeiaxvzJ89\ne47rvP3WO6tr65DaXn3tdU5VnJiciiVTh48cJNzpH0mureU5sIktzkVoDKFJGtxa87+1HewyVB3T\n6tZobzsHxt1OUu/2IdpBbe+BOCxTWwCnq5tVyxR1CJbS4t3eYL0Fgb392rXb0ksa0yxLXbbXOUTU\n0BFtezMV33J6qcIdBS8QJK104Zv7g15LfBLpgPbaCy94zNwOHKYDYPU+0dY5wxzNw1kXTXDB/+2n\nfpzDU67duAy4H+1LcQopjR9CfX3eSCxbqdnhWDDVv1Gu08FLF6cgJPQlblRrusKDfJ+tOt+oyNPc\nzCXI0cfSX0l8lqL4+nKwDDkrOtdybBiHGtT7kolKIS/EE9rcSW+0pmZq6J/dg326+G8vy0P3BUL9\n43ERWqytrdOyk/ruI0ePjo4Mk760//rP/YuhAbqPJvrTsnqSt6q0YhFqQCW+XqZxrj8AlZ5Y+OUX\nX2Kg33/uOWhbeMYM+I4TeEgb8Ma+/KUv0REpl6UJsp/LMhSS/wS/J06enN6zH8b/kSP85DS/AQ5s\nYJCxWDCXKx8+El9ZogC+lkhA5TNnZq5jDahy/W9/8Ad79uy/cOH8kSPHJicmccvINPXTWydb5GhF\nnHdXaljby6vZ3XvHcmWDEEkif2obI1E6OhDT9A8MUDdmqOIORagWYyuNBPCUN8ssdh575O4U6820\nznaAfNM5N7fO3XO2efyO0z0ZuCvu3Z+9vxhd+KWT9HS3wfCbl1WnKm1mW123UyOlvBrNo3VVmyxu\nSvKFKF31pReVmownf/jDH3icja32Mt3rf7C4Qx8mQ84xN8985AFgtbPn3hmZGCnVKtF0kjom8i9F\nZJ2zDb3Bcr1dbVu+bp5WmT1GJeJLKy3h9grAaEgyVeg0rab6yRGtdA6kYaeCcUA8UXYcFEf3l3gi\nie+KO4Mb1axVTJVKA5C8+QTC7ju9G0C/ysWctK0M+iJhOfCV5ly5bG5hfq6fuBjg5Sf/9q/RIJfT\nvv7Br/769Zn5E8ePv/HaG2urmf/8//235aV1tPja6uofffFLcr77RubK5Ssf+fjHaAM2NTn5/nvv\nJZODRM2Eqp/5zONDQ2NPPnH0hRfeffKpD1FhwhcPHhxZXs6GY5xiaczOwoiMYNVXluXIDepUCEf+\n/b//fVKR+NlYus9//vNPPvnE4uLC1N4DF85fGKE3ZyYDvIPOZvqw5Wh0+GpQW8HCkqlkLJkeGkm9\nf2kBAWbv8ZygY0AIqguaR+tXDdGog4m2QkZzS63u9MdvyaXZRB53avfeRE9XfAWLVCeJd5V6F6a8\n+Zi+zZDX7vj9prFF1JKAWiV1Njs76cOKjY5/o0ojuofrKoYNHnK+kGPd6VUP4Mf69/elv/O979uN\nJc3B2ZFL2vZ8PeLuMZqRAP6kcfcdBzjSjz4DGyuLCaTHsgejEV+jie81HI00c9nKxvrkQD8nhynI\n3NP9T7GVjM2ekuhr8cfV2atCeWyqZquunPzq4OkEpa9kmHKkgaEhvguNnC7mqXgUZFMOVCJvbDld\n29g59VI9dS8br/u79NCUoogmxAf2POe1h0NhtDabdGV5GdG3b7v3r37zm98g605fpCtXLhPMvnv6\nXTL54+MT0qsxl8PiPPbY42iMhx66Z+/eg8MjtMOekG6vnhDnE/I/bgMEiUF+863LTz35EGgmbDZq\nT//gD7+B6zY3v8LTyUk46wV6iUxPR37/979MZCyHaCaTI8ODS0uLxFhgnUwQdzS9fgWgTlbKsDWK\nB/aPLCyuj46MkNnl/OF4PFKtt6/PLZC8z+Srff39pUp5dCySzUmfBtWiVPxpKXeQTky25Nill4Du\nS2obm2nRrkBvQTTG9sq6rjNjusZO1uRmmxq9f6xtSAtrqzdbF0zQbqvVU1bSeyNH6+9ufeAWvO9q\nZ2YzzNgsE2H9NwEnd6uZhlDGaLPMUTxUherihHgi/srLr7ZKM7d0Zj5I3GGkUI5GyfzM5St3HTti\nVkrZa1f3cLZntdrXqPfXGwdi4bunJo4M9Q/j5DTLjURaDsH1CGxOxMXDIONEh2Q9WyLr9TJjqqpy\nbXX4CclUOQpTglfJK/HVIAAq7aOJ6yhELpfYrtBm+pMJlVShlLi5o9dVr2fYywfR/+RgCq8cJd1Q\nGoId5SETSotJVou8ld2395Ennnz8m3/2TYgzDz704PjE+OTUxH33HevrH3np5Zc/92NP794zGY1F\n/IFwLl+iigWwkjtDraHBy40bsyMjg+xamJk0wUN8/+Rrf7a2Xj595tzb77xP5pW0KM4HzpM63+Yy\n6MG5s4KZkH567LEjzz33+mD/wDPPPHTi5B6ank5MDnIAYDAcmxjvy2009+2FQ5n46pe/AQGTXBq+\n05XLV69duw4pEsHdtWvgz7/1g3vv3ffSS6fHx8bEl1OgqhYaVbvpdV1js+X0lhJ1P4hubhi3dGYc\nd9vhRlYPlV77F3q2u5LUUGe1anHvHuisCTbbmpNtoplNNT6nU8VmauamtCIzXWuTwqUOhG47HYfd\n0UUqrjrxXbwP2cuqaoiTRAt5+jCq9CS9IoNXrl7LLrzb3V9b9/1g7V6sy9EklLSTtP/Wl776Nz/9\n9Pwbr8byuVOjY/c9+ZGxlWWW4f577hhoVt790feGQ57m7gM4kkAy/IddCUk+Sah14JFgkpbQvBSt\nrq2YkEL5IT3CQUwwXWAYetHs4C1Q62jlzkEYaHdgVs4iWl6cGx5Ek3LAU/0vICDtIGJInpEDUokb\nODUsECCuLleKYk0a9UGy8dGQ5+Of+QQX+qVf/XsIQ7kkYUF6cGAtVwtHAv/7T392daWu9o+HQy8G\nR4BrziNrr7zyyv3333/x8mVKV997by+o5S/8wi8QXzNuQHqdbsSVBxDEUu3es4fulUg8fwI2Gh9L\nUSdFBDw7W/uJn/jx/hRnHJcJK+lJBoxKxeClqzfWlg3SBCuLCxy2+KFHHiJdDJ/+nbdPf/azn6MT\nVToZJ9ZeW6vumpyamSlgIctVstRypg/aQ47TgeBBH3oIuvjrmydGGpvkxy7CuLOc4gM6YexsGdmV\nkC19o/HNnk7CO2kC25D7W1Z7bBUrKfOjG/aqCvCOc9O9AmdJmfrMV1Wv1LmIxLXS+VbvHAF8IiHI\n57t27bn2hrHjQMz/WUNWaVcf8VthrwkxqTo/M0wX5MvX3r90pfXGOxz3l8zm/uw3f7Pm8w6lE15O\n6DWanFJvW9JqQHMcUOJkglTjXWA6GqRWVU8yo3NoZsBA1sGgA96OZyKdSuX4GLgxRXCcmSuX6qXs\n4rWLJ48dAIe/JbH05qfY0jgEqQ5nW3A8jmCjcoROQJJT+cyanG2oEQVpDge+xT8Nb1Uy9uvPP3+e\nkou/+lM/AZiLs4Hyxk2nZO7OE8c/+tGPQh0bGxm5/cSJTC6HHDNuFDaXe/TRD3OddNqYn6+xWmwx\nrv3AA8f9HBnUkm57c7MbfBfXBbfkd37ndx/90MPA+YyAqBmHBw+eQp37771vanzsmY98+Hd/97/u\n3TV95t13HnroETpf01eemvFoLEShCtgwrc5I3J46dSocNpeXC+okMCIkb2+6VMvi5lFHruorZnXp\nLjuKG/6CIrftBeDmzW0IdmSXtiPlZlfNdw9d6iZ9LZ2c0snErn/vGjua/nVtN42mOUJGjoelX6kk\nd+VMcU1YJlUhLV9xJ+TwYPwZl0z7jqRpt27rg8s96gAJ1VzJa9T/ya/85Nr1K2vXrp7sH/Bly6F6\ntbhRwg2h2OFKLru+nt09PJLLrLPuotttXZrtqNN0mnIkVlsO2Q2qlDk4r2pSwKmUHLEYgqlOPMoj\n1+W8M+lSQ+XajRs3rl25TCNXevmPpqPCDqSXjeXpVjz2mscP2rSAGdLRrV4BtrfUYVuqVLwVDvol\ntfLjv/w8t0RYGe53v/tddMNTH3mCUqOf/pm/ef78RUT5yrXLBw8eJDFL78hPfvLjM1cuArPQ65X9\nKaectyBA+7OZqutIYS2aOy51hpwsQvkWgJT7/jsX2DYQG5gQkkTZ3PrAgHgm5M/o540powycaIUC\nEQquwCLX17JYCXqMEXcyTmYSeSgUad1vZTJSUUVfF8IDfCpmgLwV1ciG4v71kAWsHn/b6ubzukU3\n2/i0m1Kout61e+PLzgkzrdaODJHuua6jJcdtdfkC2o+kHSG5PYIQbdx2dKu8GVsIqtM71Mfavf2e\nTGuH9ursuka72m0CpRs+6vI8Ejs4CRfOvxcHOoiElfC1aav7G7/4ON6wqtEvo/dJtaBr4TgRMyry\nsa3iByjERDgtebS2r+XWwjGzz9v+2r/79Rt/+qfOxfNUpUVtT71SHx4YX882coCH+w7MhjztvtQc\n6lplKTrBotGhAMDW0plRmUDabqkX/g1ODT9pRnll5lpTnccOGyqfy7BHabnRhLaQaxzeP/C5Tz6z\nf99ujuKJtCuaAaWbZmIKpPSJJuaKdK3nRJ+zoA1FuVzqnqCoV7aXrOrZd2BctSVYxf++94HbiWEd\nt3rP/bcDpPb1g3+ETyaPkEA4efsRaDOY0P0H9i8tV4IhH/13IWdyQM3cbMn2wnRzskuZ8YnUH3/p\neSg8TH3fQPrQ4RHK1zmlm27xb7/9pmK2mJgICtup3E+n+rFful0wrcJ0KUYylmAjcW6CScpOoRG0\nLx8csFaWcc/NjY01ovgz797A86HwfGgomam2b24yan5wtZ6OI3txkm7y/wMPZLyJuNtV5IrDZ23j\nVG5Gpd3O1x/ULLL3eL2bbYhp7dgYzlYf+o5bZXeOBxZgGzS+3T2pXUH+gnnTg82Wps2c5iGFbarq\n0N3yrbaa0KAg2trvsySO9OCRUIl97fzlaqFs090C5kK7HcONlIPnzKrf88Jz330xVwmMhtfsZEdx\n6EICToRTFhXlSnjK+gIN49I4m/22oz6jqtrKc0oiw1PdU2yOreSspHJ+Y2J44EOfuPfeO0+m4iH4\nZwGpc6JBn9XWzTGB4Rxbn57QEBvS3loOSx04b27CcZtAWVetaFYVHTCcZ7//nX/6T38hm72TZgpU\nHqI48/ka39q1e3h1Lcu3AGr6+xMnTiTefHMNVJTq7/19A2vr1V//jX/3/5P2HkBy3fed5wudu6dn\npicHzCADBAEQYAAzRUoURUlWoG3Zdw67si2n9e5erbdut+rqbPn2bi/UrvdcW5t8d+v1loPKsi3J\nopIpiaaYA0iCCXkwA8wAk2c6537vPr////Wb1z0DSKpFkajBhJ7X7/3/v/8vfAPNwd/+p7/BjXv/\nvTlu0QsvvUVgu/3o8T/+4//8y7/yeajTmYEktSnFAofD/fd/fHAophCzAtHJZit9ovCGZi/+YU2l\nR25QagxmYuAdLlw4D5Cf43hpcYUNubS6wsH9Mz/zM7NXrjz8oZPPP//2ffedRFjB9WY9waVpml15\nSGDpe3oEO2Bpbgpr2ZHZ2Z5ebSUq+o8yGbf1jKk9Rbf8Zbp9F3VE9E4hbLMD7+5u4fVdaxuC15Kz\nFTGjCMD3Rtv2Vfjv6Byuri6FRQDTqwhUMFaUOrH0Uq1y5UZiqpdl60AYpR3CM7r0/sXhQi1txsUa\nx2xtlKtZEIKheLberBj1UMQ4e73UjNU11Vph0NrtcAw6e3u1ZRXI9XAyuuVZW9vol6Qmpket4wMj\nGHXh+TW9awKp1PHRTILFXc1vVjbxxcZCz3WsIJ1AN9c1j8e74epl/REHm9wrZ9ppT3s8J9cWwg7q\n1//Bb15dEPHUsDQB8SAjYF8fn5woFLErEo79f/j3f4qnwh/952c/8pGPvPraa3fdfbJQMoZH4z/z\n331O6cFzfLtM2dJW7J5T+9fWHBAvv/O7X9jYpBgwynnGsSLM9LnPPZVMMpF16MNqI9+pqdFnn32R\nTOnC+Ys0H5999tkHHnhgfm7mb75O5xF/+Sl68+RBInS/uvHZz36Wj6nGSPpymzjKJ5taM8jdQUJs\nq6/n7rBMu7wG/Lxlx6W/HRIcTGwcp0NoSd9WbS7ga87cIrRvSaL6ytfGrbjk8sBsz7pM6KWOzvnl\nt8SkF2gz4c4XakKZFoK81KxT0wdAcCBDbQuWizNA+2Y2FYS73ekxBanreLcLd5AGlT8agoWNYqbi\n9CBTKwVRg6MVp3tmPwgh7soMjxwbvtN2l+0e/d4F/die9ogFb9PztHKNLbqWXH9Lpt0ksySiyGH/\n5E/+5MkTx4t58RtugW6HAgsTDZWyBvNZ04mGechSy6o/vvRaV01ltXUIWVdAL/0cJtTmHvjZf6gI\noa/MED79ve+/8IVf+ckvfvHf3nXXPVILRlOTkyN0z67MrK2t5pOJ/mikZ2rXWFNU/BlqosQbOnZ8\nL7Shy1fmR0cmDh4Y45cWC8bEJNkhZwoYPbmqZA9mpcbSUmNpbvnpp5/+uZ/7OTCVtJ/6+mSWQXMT\nO7HXT79B8froh5HW4NHkPvHJT1HoXF9a/Plf/FxUIDQU9Ri4AqaT5Ofue46srdVO3HUwu0lZG/L4\nMjfREusaavpReQtu3ibJ++FhJ4ZRxxr1I4fRVuft4Ek5LS2ELUS+NuzM2WbVHrjgjpbgVgJjdiHy\n/YLY8cS32qNWpS8k7rNK2z7e3Fxr23ZLY2Ryag8IDil+RQ9KdAa9EZi5xSQxvAxMdSxi0Yr0QwTp\nDMwLC+lWOARNR8ajDQRcLNp3WIMDyomk0r/9j35jMRmsalShpP4R0lbG3up3fT1hxFYFXWPbYAQv\nXDi3PHv+vXohGY/hs1trKCVNJB3jMRiIFSj6hMxYvKb0xPUf0TixxWG1ptQ/TX3her6hor4dSzre\nsM7UkGct66STWPvRz/3z737v+6gKwxVaWi4zewet/PhHn/jed783MjwpaCSoHh9+cGgwfOfJw/A8\nuLe0S/szCZReuSkb66sT4yPoZ4ndpgGAzli8sY7fyDLmq9cu37g++yd/8hc4yf3guR/cc88pMhNQ\nqe+/dx52LkMurPCgEtKbeuJjD+3ate/QoWGwOjC14Z8Pjw729aPJaly+shiKJAE208etkgFi8Vd1\nEVKoVOVR10WVyt4Sou5MZrZivdu91PwRXZcF+47yjjsqsrRBL1vyd94LquG/iBIrQp3+ZLA+7orf\ntmGaO5GaPBmCznan9OnF0dLr3qhCU2m7QOkAeo6AmNNi+C3IGeKENPuRxN04/cYrKnXhwKFTUWfZ\n2yoLUzO0tvCF6t5YqisuFgZOK94y9uAUni/Fa81aCTKTla2U04NDZMFGJJYeGeqZHDt07MhKbp49\n4ej/qiW3WnBRgawV+cCpFM16mS5JlGal2UxYRlz0XXl4WCk2h/vTe8bH+lOJcm5zcWEOLCSGvkMZ\nqQQY6Yh6D9hdtHzVjdLpgEgKSx+nJvQ/hb4MMic9mU6loxhslwU7EAgL1j78+GMx4LzVGN3AfQcn\nhSjVNH7uFz+LnSnBanwytbGWR2KJ37F7TyxfQpbauDq7euadNz/1qSevXrlK4fDyS6+fuOOuL3/p\nyzyL++47hXZgbzy5uponmOzet/uxj3zIlZZCA9Qbjf3M0CAYicHBqDxumzPBWlopDw4mzl9cI6Vp\nGnYi3Q+YcDNXJN1MpvsjcatcM1fWiqZ032CmRKrNcCwZbop0LJ1fp0s/w28q7pjMdPZY3K41vQOX\nrnMPdDXLd1RH8tsIwaTTL5G7XmSr9Ow6lwLzgZ2od8p9wyszQ8qZQ2b5USX83T6F5LVHxlAUw8FD\n63V57k7KnIw+naUVhj0IgyuzLYjSqLa7dREZxmBvf7yHjYQGl4O86ECfPTHUCw40Gh8/dsQZGXg/\ne70nHjyUmn4er6BvbXMpFYG99M9tkrqzQ/BIJ8yPZHoyPbHa1Cishmtzs8DrkeXqywzT10KpLDOY\nMbPL2k1EtxQbAhmTM5M8TucqW4IoAtOR9qu0D3yagbLF3EoFp3YPI7fU249fLn5GZfyhlleXd0+N\ncGl9vVY221pcug4CYTMnDbjf/7//7Cc/8w+/+a2/+bVf/eWx4QnaVmD3d0+OXsoMc/D99z/78/Tm\nmQ1965tfn56YeOozH683jFAPqnc5pJpIaRYWMCejGBgmzGyst5gcKxdI5F0Ti4s51aCsMoWlBt/I\nw17htuB30FpZq8ST8d4kuhoiAlrE8SEUzlcMpSrcTCiFb/Pmye7N5LICvXmra8Vvf6ntEnMeEsbs\ngCtJ5ttmMPlppf9ItnOm/OSqq2hWEqHGdkUDT5hbx2I3+A2iZCZNCTPYI5JLolRFh50uK0N01ZV1\nfdKt4Zl4eCg1S/2jKUKIqVK9APIWfkXf+HQMd4lwsxyuj+/fixV3OjOw+9Bt9Z7Eiu3WI7H65mbn\nREIkSRTOMeK7kHfk7qKxamIpDGcBb1RqCeI2U8IH778P8tr89cXz5y4isDUyNk5Kc2N5oycZUh5m\nCR01tH8oH1DI6UG1vtVx9UeabI6tcJG2llb2xX+8ruVXzoB4kZqP2/j++3MIZnzpS1965KGH33jj\nTWgp9N3ZWFMTk+uKj4TN2CNPfohh6u3HRFOSWIKrBw3Uu+46yoGgVFykBetjNfl19ZrrN0H9UCrM\nki0lOrPTDd3XYOliG3Wmv253Z6O9aNq3VSQMBBTulzI6fbQcy9xZPsnaeXGbTZ2cKKdYCUi8cR2/\ntby1flk/nwHbym3RrXfGc5xXPBieRBeTMNAG7VCekdvhBOoHt3t/tuyqlz3p/oyrCwYxEqPaA8WE\ny9DS0uLe3ZMMtoGojKbCv/d7/yS/ds4yNuKiw4GOV6qCur+BcSSKqVXmSvIeZX8BQY+Uo2WKxfF4\nPFws3RYNf/zOO+NudQA/+b7YniMHMtMTRbeFlgvTFtRlJfV1m5pVA1rW70eJew/wFZXO8THkDPEx\n184RQgrACMTRav3sCsoIpcfv0n7grSyvrtITJ7pTT9JuTg8OSsqu+i06wOvHxwuK2zQ5TzjMEwFQ\nKPOENkdZL3E/49cm93K3s/YRnKb/6x//6eTk3u985ztQp5dXVtBXorIByTA5tQv7qENHbhsaGX3s\n8UO79x2f3AvbY/fYeCaZ6o+L70JUQPx4ZKM83CAvU+qYymrXkRIKJ5SQHgEGF2VLdB3srsFwMPgG\nZ/btTWB0AnY7hsldwhX6V2iVtq6cxHTNHZuMpLmGYfq46kBgMH33Ae0E76lDtnGOvnKYbpDFlImu\n3gw6GGvnpmDrM/i2A4Jy7QPH3QmY2f4MbTrL1V7cugHlfb8EPeyFk/HzF86/8eYb8L/IciCz48Zw\n7uw7G8tzgKZp64mihhlpKVg+2QztRfFXk541aXtIEqRYCi+YpmjY4WednCCix6P77r3znic/Wk9E\n1iApq0aQC0u61kzTC+rrEfUCibgtdTmutDLbK81Wautcp/Y70HGqtQVm1rAIfQiILhV3GJguYu39\nmQz3DfxItQbUTHanbjiLqFtEtMTKlVJU7jU8dPGKBFU1MJARwRllKWUoQBjK6hiAQ57mv5UV9tEK\nXOYyF4Q8GGfGHSdO7N6/b8+B/XjisRqJ9/Tg4/29NRNuWGTmhgtAsuAgXR/ezOvYa6HZOzAiMBju\nT3sttakSml3W3FHmIRjRrc7OYMfnd9SH0VipHSc4QX33Lo6pd6S6O4i9KPJeK4gC8KsfeJtqXBdT\nPE5TV5+8yOBAXEyScSby4o2ogiqgnye0xIGgNZ58P4/twA+1LbsHTDqZ9oWzu+qNkKs1RbSejNYV\nla/CQYOqz9HVPzSMtRcWJsvrWZJsfFwo/y+//3ewnmDmtZQEKVoBjncjPB0Yq71t3EKjPzHQBNPo\nFBYaLcSuzp17+99+97mTJ3bfeceRB0+d3DM6HoJ3l8/RMUAKbGUNg3jpFRLLZfc2mppjUWv/4ZOE\n7VS6RxcwYj/WaioXBs9nxlHdXGK5rkQLipgH6mx8dBh81OW5q7jTbayti658JiOGns1Wvpyjd6fP\nB17cVG5w+o5xqG5PArVEhQSL//U/fm3/gZ47TtzBnHdsYkzE5Rwnm4ds7VQboUK5MTze41iRVG8E\ny6l4b6KMtnoUipoUitxxHjaAS3wdEBiQJokSO1MTcP2fCLnq/nSHNbvb9dTN7YInXT6gvsJbENDV\nJVkajO56oiRIknbBqhewIfdW/xbX/9tUWuVqZmTqtE81sFqKNhHRx6K+fu14w80Vxpk6TLVXxNZI\nyGlo+UieHE9CaxBsh4sFUQxdMDIzkKRZ2/aJrVBkakLkb31FxYPJVsNBwC7XKyxBDIxK1dr0nr1R\nwZHVz7z+d2aoIS5stOqgJyGpJRYx/G762k0lpccpxhgbs8iSyA/Wiqi+Qrie2rfn5Kl7kcY4f3n2\ntdMX//IbL3z1a9++PH8tlhkamt6fGpscHx2Mx5NYpopAgJwJKmArRnBMNOANvSh19uwfdD73xRfn\nATrDfQfKqN3jmJkCqOxJpeA58EEJ2/VsljvO+7XbArTcYX3/uXo2CkuM31hRzu8Ka9zQf2uIgeDD\n+JMrVPNl2Z16SBBPhYsb4jEGRQy5bIDIaxs16P2rWXj+cdY3Dsf1psQST37Rssp4GQjR01uFrmsE\no3VoG8h7p392cIiDoS4Y4Dtz3x0Oii6lAG1W4zjB9Nfc3pnxPJgUGGM7a0YhyRmLlPUTiioQj9Yx\nVXColo7Eeq7Ei0Cx1RNN/Yy1gopfuQZ/r37qQfKHd465AdtXd9v7ci1ny91eB2dH6XU4sWSC4SoA\naXiPDQUVabRM2KPDIxMy3nFMJVotiQthSQZRprOtikf7qJUrL/NhQkzmq7nF63/wL764ufoU8fWd\nd9559c3XL87OfOOlc3/90jke7dBo+hfvvu0kAhLHjvcM2uurq4IUioTphGI0LcQmPLbZWs06n3fF\nxD1qhT19PS3Wqblg3FEWJ4MCCllldR9R07MmHceWGBYNM3MlsUGV+sLFc8R4kIJoHhDgtUMW713X\nqUrk3tqxRqKMkSfy8V/+Iv8C2EACDtOE/BtOhqEY+1JgGYbaK02U+AiUckktF71STiuFPmUFID9d\nRfECjpVKKFWBL8FH4jy3VRD6IdWPDqSkWq3Bb5MHvxTcBcEStjsLN8ztiUHwoGgvL9N1O6wEbKtN\nfTY8bVoFwla0bQBvLS8HpTktiO1oGB8iAYpabroXUDGlKlqEFYUSc0QihsVjaSCgDGI4CZoqgOmF\nrg2N9ZnQpfvup+xdp5Mv+RuM9NtwO949c0xHDxU0ORmsnky4Wu7c3Dy3H/FNfJ57QvipRJ/9wXeM\nRs7CILCJ4WZEciJHcAES3WX967kqfhlWyxaLQwn1prhyQFn6/Oc+vXH1arRZOzw99fC9UD6O9Q31\nVtxayannGo2Zt65+57nT337mm9eX1yem9xy87Sh5FIpxA4ODaHoWGEbaVjIRl60mugY9pP4+gM8/\n8Ll8HK8tsfVsNVT9x07UnqHEmzz9vmyWcTreIfTKi4XC+QsXLNUtUImTSCBo3JgYjwX0/nVjXlcR\n3iHz6d/8F8RsOkGsXmgpPB7QWuwz1jXOH8z7kaWBi4LwZbXMdnDwHwjZWvbZUzlhkZgKXGepe0Y4\n10A7FlZoy4/Ii/reKnQMn5vsd2b8eYqfrnSqtXQVtmZ3DrBleroV9f2N5KNG7Q4jpK0X9Lsrgaxa\nt1y4IXFlAx9GH4pbioAJ4hAzM5d4CHwjIjxg2vhAHZ41bYmqJyNB4Y3tPvFdzGJ/UBVS/nxtFe/t\nmnpqXOh68rr6m1R4woBO+HIg55ZXVlEsTMZTfGF6dDiRtF959fv14ko44ooXtsVTVpABWXctf7nb\nchKH3BZ6G/gyhWot1r2R6jE+8bFHWo3NvoQZcStuNdsftx86efJjH3pwHPstNM4JqNFQtWW888G1\nr377B9/85t+EwlHAIEJalbxF5IBDipfE4hEPM1P1xVkcEtfbHUMHPomMyUQURrRUlTuJYCTQnrTw\nGIPiY4lXACrbLu2aA/v3X5u/ls1u5ot5lX/KL+IeYoWmGYQqiZV7Jfb0QiFsgKgX1NwTn/9dGdKq\nbZDN50eHk/BIudfpVAzFgXiEVV4ZHkytrxTZf7yBUl3oLlQkllrWvGgqGTGloyv/e2ZZquWrwilS\nOS3V8ejO3e128797HZtGMF0JLvft2oudNLSOUbwIVbahQqLDZgckB7bJQepkBhQnCZ7SE6ajX6Yu\np721urZEzJhfuMY079Kli2R03M2pqV379u0FaGtJE414hK6V9AfoDNDT0CACXdRqgJ5OWP1r1mxL\n/UeoD+2A5C1xo8NLpyu0ayt7wQB4R5OubQlVcUfp5zHCm5u9urK8hs4MxOe9U+N0506/9nfF7DWk\n2OmhcFHSXBHEWHC526ozQz3b35ITC7gAYmWoihuHbx85uH+8mF1263kcbML1slUuJpz68cnJz37o\nkcE7HijVmvMLizzYnlQUW75X3/jgL//iq9i7jI4Mj4+OIgaPH6UijIckebC9kZDZNm+zFcpaUomW\noxmuIdkqHt/XEI9oESjzDLZUJsTHu/fsoXiFLgcYYTMrUmdi/dKo+0eH34vUxZXu1tsf/8XfwXjd\nUsbhkJ6gh4vZlqHUgUMRsWW0KExd5nUClmMKXReHR08O3BBTaVzyKAmELKfqPn3zoEBLikD6aIoY\nhWIdkAE4Io5C+yKCBUqJGw76QR2pBAAJL9x9HPxMES0R8qPutasPKBlthQORCiSTQWhczMgrIsED\nXCyM7FhvmotvKril7GxSMN4n4dYUUCjzLDnlJKmg3Rwykr0ROG5NKXRoKdbX1xGtuL66tHT96mxh\nY92pV+O2OdSHEHJyfWkhQXbXamTXVnpicXrbaAGhtTR/7RpxilvEIBBhZWX12hJgN1IzlQpFqu4V\n6N6zHrLuiJkRhq0kfYFixvXGSY7KrrTIjFJQ3MKTSTx3ZM1bkjHKdiaIcStrqlpd29iYm78WTkS4\nfSeOTdVq+cUb125cnmFJOGJjXU4inCocUKkyGPuw2VUaSsIPKceuucUIQ/8mhXizN2GMjww5DYze\n+6DnA98oYF8csUqNSq68aUWN8R77yQdOPHDyaL1WnJufL/OqsVjRNb/76rsvvvFuvHfwyNHjqEQ0\nqkXEIOXsSPYW8kUJChEsD8gGQ4lUuipO6wB9xXebHdeU7iToHpVW6iVuaZF4SYOVYyVyV+IxNoo7\n6dg4mQhyL/QbpcEv+0SCgQIIO8r+2xEBdIWbsD/++d/1pDaDTV6FDg0Iom89DGWHYXt33zQClhWd\nPUGdE6syKuSbMvh/DDHNi0YVKovLb25h1lGtYgmqq/Q7057PCdWIVhlA7kYkSqR7FefQo6IgwUIJ\ntr8/jlwrnrBl+HxOq7eXEywE1QF7LTA/5FxcfAVlBpTm335v4drC4o3rbB76BQShq3OzI6PDpIkh\nUbDYuHrt2uSuSeqhawtXqffJd4H3jKBgj/jP2CgasunePi4qm8tLjo7mRyLFss7n8qCddNtUjwAZ\nB27HRQbTd/+A2ZIzCHyvubNK8A4cUwWTEm4U8qNcFSxVW0zajKOHphjpbK7duPze6Wgcf6+ypRR3\nFejG2sr9DC9MSVHLtDREP5XarkXA3zM1PD0+XM5tsFg58+l1IxWj9EbjoBpZWSToaEaAmT1821Hk\nCpeWl9CSlDlArfI2CkFvv4mTBd59V+bmmRkV8jkWgogXEYlEV6OVzWWHh4fokbO7t3yvFBBoS/Z+\n28SFGyv9F2XeNLVrFyIynAyzs7NQ+OtKDEKbfhJ6lMRaXPM/7E/80hcDHUDXnwe1Peq21rpGt/ol\nly920NUi7NLLdUQ/wjJ1mqnCvpjHuiIjLISaliaehdR7k8fDqIHlWxF1Hu6ppHEER/03RS/nWgI4\nWhNbzIQ63Rh0F4UNzOggBZpNNieKC+TZuGpeungNqWNERK5d5YMs5lRceyJiLl6fP3HkSBrdm/7+\n1cXFA/v28pZoNPeme7jpyJ7EuYUgsHdPUbXv3r1neGSEkrtUpsdVWdvIrq9t4LyAZIMVCpNHqnkh\ncrDCuM1k+huq06z7j2REuj3cpXwd7FzZyrZ7+3L38PReSHe6TI89nQ4zqAxMrdbAdo6WA1kNNm7s\nUjbh9Fg/vYqQ0XzzpWdRnnOaVfEnENiJrZa71bncRYlHPotfqlPnQOWtjQ7Ejx7aV9hcbtWLfb3w\nqFH/rIlPUyTB1CHmtOiOE7OyG5t79+z+zKc+Tdvk4sXzbBWCd6HmLi9nf/DKC8Cv7vvQY8WmFXOq\n3BPxd1dpBusn09+3srwkKBeVAFumF0S1B7QnqRMscpT2A/cWGjjhHL9H1ChIlUZHRqanpvhOUlBk\nNvhOFFmoq3TrTNmst3R077ARDc4cde+78wh2PAS/4ZMPHKXCbLdJCUZnpLe2IpGrOyryX0zUM5Ux\nqC5xXcmL+A9nSxJoXRfoSadCROjN2lSICakgidyqAWIO9sYqperm+urSjUWEqeiFra2sXp2dQxBq\nc33j+NGjQDIwr9y7ZxTCz/PPPVsrFBtVvIiTN65f37d3H8hNjumhYZoYw1DDsN4Udzh2D6bhMziV\n8OdaNgfDy+jPDE3u2sXZ2Z9B6Cpjqnof2iEnaUwFD96jGLapLiQ3l4gCXJlH67dltnM4VClhdrkm\nmYExme0Fl60pbwdnJbDcTWWwyvnOgmUdodnA3+meXqzFMH7r7Yk9952vsYhZhNEwA3/4TTsud8kf\nGKRIzulIAskUqD9tPHDvHS5Lt7xhurW0eEzA0qTBARk8zfItFYuEKAD3BIv11ZWJ0eGf+umnCvns\nufOX41EIQ/ZSrvnaWx+8/t77t999/1Q6vJnLI+PMDJWih2pndXmlH/1ax+Nx+Atah3hji361tegl\nLbFsSlg+oLVO0h9SGCOADIxjkQJmtSDRhcoiT4EUX7jqyjKV6P67ARMsn2Zv6N/bziSd9iKW9dpW\nt9nCz7bjU7daUcD+Z2u0GRL1K5na8mB4w82Gp8ogqrVhkg1hrTueVyeoOFhe9GGF60V/bHgonM/V\n0YW6dhUs0aW33jzDWmc9HTo09eKLr/KWwObfd9/d+O6wzorFAr/77NlzUnmn+2Ug5ziPPPggX6J3\ne+TI7vX1PFJ+KOK/+ea7V+dXaJ/J6WaH0PDDJ6c/Mzw1PY2S1hDE5GiSPiXhChCbjDEazcHBPoof\nPmSJs9xVPRqR+GrLctcAYEK+hih2WZF12iVszZK9CtXdUm4yPQKSs32EbHZQQ0QpUoEBERVySDQu\nXLyYLxQ4NqEODQ1kepPRv33mG24TaS68N6T407Jqncu9pWGRutTm/VJR8iBSsdajD93tNvNocpUK\naNMSa/pprVE+JRPpkFNjzTWVYh7xD4EBak/SmCce//DJE7d/cPbswkphIJMo1RvXFte/9vVvxpvl\nBx5+rFCqgHgdHB7mjYUE9FKJqYGGbVlG+7BSrWLXMnfQ2NAf6EESDReaKKT29FSK+QL3gYwUpwJM\nk9C8vnDu/Myly+yHVCLJjbU/+ctf7Iw3W4Wt/qVGZ4ebc9A/AdpHs6NTmjZOtVO+0FXjSUcWtKVY\nBV7aqpQZeH9RKdqVII8IlkobFBZ2by8DHQpN8uoa2diFCyhxzKFZAO6IWzM+Pnbw4BCS3AMD0L1G\nX3rppZWVDdBsp04dWV/HrKrR358WQ+0m4+vUiRNHWOv8IuI+SjgzM1fQUb4yNzczu4DcZE8fXJP0\n3gNkLON7906YNiI/vdSHq2tZlm8OJ6sSbVjAT8iox0S3PCRsf0Co+L3ylkl6xP2Prnu9qRKqRFMg\nHLYe4zGR8IWwt0ts62jR0tC3bdHdT1SDkncdYIq2voDfNmVx63oMj5P5hYXVtVWurSdi756aiITc\nt998ubixzFIMS13RUhgNOyAypWerrpgUW7ZwZpSCDnVVNNR66IHbncYGor/V8kajVkawCTGBOrPW\npoMNGN8obZE4QqlOtcwhkGtVy9mN1b50z0//1FOtWun0W+f7+jG1jnMvzr8388pbp++694EDh267\nfgPCPrUGStFuWLukb9XripqqstMuALaeyLBjHdFWUXBrsvhanXUEbgYOK0NStgEpDfuWSE90p8mG\nzgULyf7EL/+Od3R0yGh1WR+2oa46tfJy95Za6MF+eSAjsrxq1ZWuvKxyPW9SYkSStSRT2EeJeG1E\nzV2BgUKBpZ997oNLc7PzG+t4guOHXAYwRMpC4nHqnntEoqFa5eMNMcDppwDlA2IYEjY9aVwx+7K5\nyokT044LT7xxTey5Q5iWXb16/dz5C0CVQLKhAjG5ZwKhrDvuRFR1MpnuLZTKcMEXl7IYHDEtLhZr\nqt4jzYqixoX3RG9fzBBMFQhwVE8whcOBSGR7lCFKWGbdqsvOnWVwSEIfjXgwSb8dqU+Vm+OQjR1L\nVX+qqhKVgORqYLkHk5makPOjonBsWtQeGLksLS/3pNIRt0Uu5zSK83MXFxcuiwYdmDBhkwrKo/2k\nHT93bziSzdHNsoS+J7Bhkp5Td+0dHYpSlJpOmQpL5j8hRg0RWmECJqF168rgmcowjnEfqAvTScYi\nKJuC0Pno448fP3rknbfPgObFdhm74bml3F8+/Qzv4yMf/ShUHpQSU0iiSt/O8Sm5qteqwMl6D7gd\na12r7RIxxX+YPj+tVtdArIxj37E8+3JR41P9ED5gxeuGr/3JX/lisJdiuFusNpUQWqqvZ+mpL0EZ\n8ScVrnwlW0s1N21FfXW7NFgUt1JQKOTpHFYQr2TCqngGKJAhl0dvBIWkfIHxXJ0mEnXQ3t27eKYs\nl6rcy+bk5OjAQHRzs6xRuBQfXDoXcPgwFKpoWrKOftOK0t2nHYG3x9JKAekl0iPkgoeGB8jIp6bH\nDh7aE4mm8X7gDVSkPehubNabYnjuKmcopHiIB03sCkdHoMCK5xtdoPX1CrwtjmxqhrDQxkL6BOOo\nomblXfMuKF+54zxpDclAMoQ5jsY56gSGa1a02uZ2jkibUmlrDcfgzEyvfrdtk6kjXJBk2JaU3IK4\nOUrinUFmU6x9QwgmE+A53OxW/djRw7VKfnVp7urMuZDVVEIdXcvd9XP3pugVeL001TGrszvuPjl+\n5x178tkbPAR0erFVpbMajqZJL8PxZEVcaipqlmSKW7RMsgQ3Tw0AHnZtbR0L0See/Dj3a+bypZKL\n400vx+9zL77x7W/+zbGjR++//961lWURYZLd5XTYY2lF2w7HKg+jIsWSDwWt1bV3OZHFioTb4HPX\nX0W8F5h0qLnYT/7S7+nQRc4KmiaeRPG9jFkSeSryI4lUpFQp0BdHfAEvzEiMDAlkQkvBPC06sBRU\nYWGuI6PHMV4dGYrREEVNZCgTob+Ldf3mOnC2zWvYQF29PndlfnlxjVkY3zw+Ngmb7NQ9+xAcAGRB\nLp7uwSUljUBYTbyQK+Q/sURM1LHCsd17B9O9ybHxQTybHKkIq+fOz12ZXSDbLoJIdUUPcXx8aP/+\nSVpao6MTSAEDhSUPobWyvgEfJCK4RbV3lXZNVJsZqXtkIygZFvNbUhUBG+UKhd5+0a7hnwCPZOIS\nshGjI3DS15SiXCaCrkKZSgwOqw6Dbr9wf7Ei0vgZbjS5E8coy117jneDBXRyuIP5mBqabmlai9q1\n5urJ9aPPK/90NJ5G9YuVTyrAL6npU6JOIeMtEddnyohQ9fT+PdA2iFpvvvKC6gy49AnwASaTshR3\nT3IawZyBLED5GdxflEdD5dlyi4L9TKUtUR86Ua/NVitrrUYp3QdZOdfXM+k0h8HQM31klAuEAV2L\nlh1pmJGKG4KujPEs1Wi5lGf5DCTto/tGH77z0DPvns+XCw2jOTDSn6/V//a5585fvTZ14HB6aFgU\nyaRQ5onznlnNjKgJ4BSjdcEVi1K8gM+o32k5ceFN1bgUrxClIScFbMhQcx091xcfBTXQsjwkCev+\nE5//Hf3ZkEhaomcp9QoHBEUD49LF68vDQxl608gHVyvVHKSmJjE1LFj5lhtPWJkB+ieYgRVg38GQ\nvHzxKknIzKUbG6uNlaUK+hm9PfQHevbuGc9u5h5+6A46JL3pweeefe62w4dpbxcLzo3rN0gd0qS9\nTIoj8YnJ5MgIrjrDExMjqKbS3Lh8eebddym9ZldXs5yd6Z6+8fGB6emx6ekJ+q3JVB97mlXBBqlU\nyPUdNbK1dR0JnrEmM6AtJSo/GWgoFLVq/lipFKkIrciK1vznfkDa5Q6SDvLt9IDSwlET/UeFlZQc\nl9WDsSBDVtHdtLlXcaoahgZV1ejV41L+JmUk5O+obtA5Fd7ZFm8795YOlmX4PYEtPLMlCbdsAw4f\ntTEsXMtlj1kGEKuIIAYqrz3/PdYQD1lcTtu7yW1rautfgh4WfobSILXr4gTVEuQkddDP/swjzcYy\n7RcZVJDUOeG+numwPcTGEUFKy/SddZw230D76el6j/+I9Ome9Kd/+udJAS+8++76WilmtTLpvkI2\n98ZrpyvFShLSWjRRLVcZvraEp92Az1YTAoeXPohTDcEVkRkKJNEatnQ3U+l16kZWyO1kJPvHqa6g\n+HaBeam2l4ysMAARNnuzpXR0K6OjSFqjf1GLoYma6Dl4oEcU/2qlpcWN9TWGiyH8uOEroVNQrW7u\n3jV19VLu1KnjIWOVFm++sHn9+vzRI4+C8CkW3NWVpfW1KRYB8peTEyPsuMGBPpK2hx+6X+aKljE7\ni5HZ7POvzPMedP+I6EhOMjo2rMH34MtR8BP7ytrWquUE9zp0bWaaP77Rwy/NdvMJGTotIJY7qjUu\nzEeQHOUQ46FISGVcknODVBIPPb6zhguWKzYpCuXBLBCEiIC5WeI9A73ra5ukhswyF+ZFFOT6QlFd\nEgZVGQ9x2h5f30KJYEdE5xbSqBv4aZvt0WugepOck9LGVs14rl4uWJ0wqVgaJlrPeD+8M07nVqXA\nMQ472qOtmJ38MEGZkIzFtQeOKS9nVMUkdL1QrGDRFFYoR0P8xhKb2fXsSsuMVsxOa07tykgAhW1t\nKwCkyInlCvqZ9jby/+BnP/PYnce++vVvvXb6rVqxmogkidGJ9MiB2+7G5np2ae3g1MRQX2p1cUFM\nh40t/9pYOKpzWglVtg7otke+UeJlIhIemAIFoRkensxWbUGKQjWmquKJDDKsKcmrMTYSv3HDGR+N\nr6/FZ2fmKWyf/pv5ib7drL9YPDkgwq30LtZyufV0L7LCQzjmXVusOYI9pvKMNyr9LuIBDm4+8VQq\n9qlPPcqN2thI0K07fsfRy5cvKry4JtpF0LFHgnhgIHniXsQ8GDaJ7pIGaRUK8m3EUXJoTREQMpet\nJ6+ADsoamqL3vRZXUboXCPeEtOmpAqDb+mfV97T04ab5YOTwjhuuVxyFIG1puR+eDbSBQgFZuF5m\nh/Qf+vt7DCdKa9mKxSk5+Fki9/DAINADgcsmEss3bvA0nQAqRou8tWW97C5g6o4C1NsXfRdtvG3m\nqgZ33pesoAaOHCzy9sP4GZJEUTRl80VrgpHaQLq3P1dZ5ehncLfV+lQhwDGV8KDAsOq2crZBqyYi\n+ATigl0EqyEIRZwiBApSQxisXlman1lZSER61C81PexhWOueCkUavEJb5q4lzlk6x6PNPDw+Mb3v\n0G/92t+DXviVb35n7vp1+K//57//f3oGR/7xP/snu87u/6//338aG+x79P578rlsypAfNJR/B0rc\nnCwkh9CdiKGqJ4hxq1y4qpS07I+zHeDtc4vN//dl6DbIIzrDw9bSksi0I44HwIg7hQMrAmDAAO+5\n+5SeGnL112beuevOe7hDly7eYAxMHoVNGuvj6NFxzs2l5VxmMAnJKYkzIeNPp37jWoOWBQ1/akGC\nDcua2QdhGzVTHhnsRCD7jTqR29Gnf8MMCmOYPoaeTEN62xJ8dd/N0OD9pDKlEXhEa0tZQC85hbQJ\nazIvq18xTaWE1xu93kbqsuD7+6Nqd8msl3xXnXIifUwqRYHKx6TgyD9xT5DtHBsZhUwpAuq9veBn\nmJ8TyPkSPBqxQyNqCOpakDM6FCk/ukgQhNxBt/HGc21qn+sGGYxtmYAt4p+vKOA5vrVNhmWvNlD2\nksiKTTnK9197+us8u8Gx6d5E5JF7j00Nxv7N//bPL7/3Ym8KV8eNsPJ+dw0ryJcxpRtRjNkDqAk1\njKwVqpmtqN0KAUr6N//6Z1Kx+XQMNBWQInGAC7v7euN3NEM1X7PSY3XpDdzSUdnW5ko8IKXxXtso\nr8O/vnpjxYwkJvYdNqPpF0+/891nfwDYen2z2JsMf+TRhwd6U1evXOiJR+47dc/jD9zDWq+LaWuZ\nNoCtoDQcQTx3X8TGEoqorcOfTy3Y0bo5tHRjmYmuyFAp0jHSpPFIYnx0jKdIhGJnjgwNcs6fP3f2\n0KFDrLm5S6HeRGtomGx7JDLo9vZxnQb+YYWiKH5VnMJb728QD5gaUTYhApgZ6O0dGHxk74QSPmHV\nYkrcZAPgWsiVlesx6k5atkXRMAtzblKFaFaoJvL6emh0bVkwrFRlGuwJJSeTCCA6XayONvnfa1Fr\nUjBJuCgEIl5QqlkKLImzAx16XkfasXafvlkIZSkZYUu5J1RYtSulgjDxGlqZS7BKdObHJybR7Eb+\nsP/AHvpvvBquzcBFxGa57V+gL15D3oP62jeL3z9iMuPl68otzY/x+quqz2v6tBJ6ESz3WrVVhnxt\nMHNtjI5PXn6Pas/x/D8COu9aT8xRah5q+gWyRlo3jiqFqQmq9dae6XFQxI5yj6nWy65ZbtHRKJdc\nxwxuY10Q8K61fFJBAomhIwsNzMnMJJdxirmsY19f2bg0tzCUjnzusx9768z70HA5yZ957lmySmDV\nqUTi3Fe++ad/9pcfwdL64YdGBkaYTNIcBW2WpzQUMrcnVKgHEPxbE5R31Bz3lvtg/0iz5h4/PgmX\nT0SiLAMNDFyWSLVqAnm9wInz6nvvPProQ/Pzi4cOjd15ZyafNzY36MPkFq6ub7yVpzKEaCj9wXB6\nbGx69x4jmTJyxbo4y2Ki0EqzoJs5T1poc1NYhulMX0k8x6TjA0CRWwoCi7Vo1sGZVJVYFDM2QwPF\nhM2oYrdeu22zAIAQjvRSlT2sUIBVoqJPNF9cQFkcgo40vY5Vw66WyuJdXKlEMhkl1hy/Do6vWCRs\n792zL7+ZzYPrxSGWDC8ieg9o44SUmDqVUcSIj0/sgoGf6u0rVuqReGJ5vSAU95abXVkn/4FGxKLh\nvrHudQnFhXHsahbCjqqUjmv8WMmM6+9uTylyyyVYB3i5SwDQa2WETEgowIpG7BjfDFZ2cnIX78Mv\nJNxOSQf9b1vBdZqCp5MGPNw+VCO4yPfeP3/44BG6dhE6ZooyZMtr5mNCBjIU69HWbg+O2oH6cPN4\nwKbKqcWGL1wugErqEYWzXHasJ3n88UfRFLqxtnFs9658qfrC62+cefcsPTLaBBu5KjE7ZkS/9DfP\n/OlfPj05NvjIfXc/+sApEPyZ4VB2bTkhoOKIpufxgtsdh4IR0NN5pg135crs1NQkk8vJyQkps/p7\necy0X1hXJ06MaPeBt946w1O8cuUyhxNfwI2D4/LY2AGkYLh5dCNqsnDJfeutaqQkNSWq9WQFSdZI\nNIkkU9MKyzhmcHSYFVyhy0R4jkmubEfsfEV2Zd2VdRwVRCFyyU5N6yVxGkasiJC7DJ/LL1FbFWWO\nwCTjbSP2jlVCNaOKVFtnFNxtUm2ZNahVT8JGesYSpxfLcmS78lO3Hdm1vjasNhtHx4imQsJm48lR\nOeB8xm0ZGIyvrJSpYi2blnxDvGNlwdqptPhDJXviQKRFmlQp5mncr26WB320O2yEm86tVXGCbvG+\nOU2nn4jjbyLlX9KKJqI0hXvEKpoUotJKRk2lc81DA2Qr0F9TxRLPw7izVJWbLz1ty1UUxBZZOHRB\na/batWTP/dV8spbPijpAzRhIW4lQrFFSy9rHERoeXELugPRX6nrPYyhQr0gdnzBi5VyJzwwkkqzC\n2voKW2EgZO0/ddfC6vpHHn54s1j9q6e//SaL3m6trm9EBvqMKMp5yXLd/Oo3//avvvydA1PJe+44\n9omPfRiNsQQEgwYaZ2I1rEvkWlvQyo8Uvp2TnDz/4dlNcn8WN8GVNHp1tQApUGy5RYlYHht3TTok\nfX0ELBKS9bxEXPmv2UHr5MRW8UxweepgbTN6QpGgiqLUi5btAxbIjmh0eB3rCN3rhikCgEw3Kxop\nzhXSLeEzHIntfgvSwUWSf9hYKkM3WKvLyzV6IYUCxaiFozcNpeXlFd4XS1xPPfkV5Fq8HRYubRM0\nxQX1mJQ0fWiIab8Ip+kTI6i6oUTqnB31Z7pItFt2xA3xepYOhIo6JLLcSZ3kGJ3C1k73HnWDYAK6\nK3624flLqguLhhJ+pSuFWrvwVaNEVztE89aoOsjKvvzlL5fd2PBQ/7133tYbR2y6/j//o8/jXGQ7\nhZDVsLBoVaI2tKoVkZG/rUTTEd8JyWJsVx9rTt12y4emjT/6w/9p9sLfJRC6qRtOOZ6O7+7tmWQy\ncbP7o5HibfV6rwvcVA0DffT52qU6+9J3TC85Ps86JBn72hsrYPdvLK8gJUxnh/Y7w/Zqla5gdaQ3\ndcfBPY+dOnHv7Ycm+9NhuIa18lJVroGOJvgZ5AxoLWAWoofc+VwxdO7CRV/PX7wgB4b27tsPLhAz\nYFaA+k9uNE99faMqtZMdaRthddPptXxFYHEzyI2qPNN2AxwTRcERG04vn1ONQr9bQj3PJ2nC80v6\n0qENfmnL3twQaKF4MCRlRyVjcSVywDWbjPSI2vzcwkJZGhFqtLa5meWWaS0k5F21z9nRo4c4CXI5\np68PvkhGk1zKAuvlLKopLJdxa/GwH8l1Wv3Z0iczzO1Ck51kxbYGuXr3rtPRutneRe6yAvf3j8rx\nHLvNK/DNZStV+U7i12B6kIhmMa6vrAkvTgg3xk5A+p1OGxnRG0qDhN8igUe11MFji/3bLdTa/FXu\nuT8ELPL85d7e3pLr67uhhasEvptM/t79T65nN8/NzJ5+5/33Llxc3lhPIJyY5EiP00J+/c33Xnzh\nPfgpuyfij9x3CjHhI3unOXvpDCJAUirk+jIDJZRNHaParAob77GPnuKSiJ2sby3EV6w2oGxFhbfq\nOJ5Hlu0rDBjtOky3PP07rtsd0hyNRXXnpKW0eYFb6beqy3P5uNkKihTzgzo46ScEHYV2DRxIPBEQ\nWO7vp9Ehbj6jI4TJ8JtvXqABQgU8M7+wZ8/0zOVZuvPCEzHsxWuLIK1JPITsKRQfc2BIClAsv6UX\n3owBUi9VVCtGlIOV75uYmtG2A63dCgkgycOg6HXmeDN888dd7kFtCUvNvHSPaDtB9kfR9+v2JGq6\nO7bw/WWkC339GWLEYpHZZXNxefXwvklIZAD0V6+tbJdfNYJpTVChQHhotsI2G+vrOUzE3JpQZ6gH\nbGk2uF1WbVvgEeWGop94F0iua7n7p5MWdNCRV5R+1Z/m2rnBaPKxY7seO7G/2rKvLq6+dPrMG2fe\nvzw3j/VZX/+QOWgzirmUy3/w9A+Mp38w2jSOH508dvT2EyeOD/Sm+waZNvSwMQDxFYq50PxibYt8\nwBvzJFUNTGKDakR6ECtjLb94cjULwfVV5dstCMM/qUPKCYmDqylMK9lUvIuG4R3l3ARRNpRMxtHs\nUpXLtiple2gwtbZW7O9LLVxb4ZOgzi+ci4NxO378BIkaUE8qyQvnz5OMDgz2LS6uTk8PxeOHWOtc\nxvR0cm5OO5aIiCQYs2y2BhufBQdunkTIspI6qxbcmHq/nvOJa3XSunVryP6xlntQkVCbUWrHG2k/\nd8pEemKAbeENDzZj+WKAXpdjS9Vxm8pkFyDW1z/TGCk+JgutzK0zAlnfyCpypAXZbfXqWeooCq7t\nO9ky2lxj06+GbeGzEuUaxsry+v6pVKWySeud8QwVCvILjuHsKBDblbaZARBi1xvRq18b+3iGP4rM\nqpcT0xQDoFMJGRkmfPHbJkf2T37yc5/8xMpm8fR77//g1Vcvzl/jx/oGMvC4CM7Rzfzpiwvvzi7+\n17/623RPjMnrXSfvOHxoH3+bYdqI4ai+uS3JQxpqcYd0xtxGKHmdb72CI+GQ30nwtY34PNk/wjgq\n+/JU/RX7wdjM0uyLKJ5ySFnqxAKcf8Mn8vij8rNnP1C6iqIGjMMwJ5qW/yNyKzxnX7Xa1+67O6Oj\n1vyN1uj4UK0hUu9DI9DJ3KWVRv9Aim8olKTFubSSJcht5go4DepSGMAffRxP/ptVQi2mILsdboze\nWfZjxva2v6SmdOh4qyvIHzcp8pIcx9k2nLJvFk355b6CnxZGJBy45ixc4EZLaXc6BjJ677/CyqcG\ntTprXt3Q12IkTrtqML3oLqzt5uKNtcN79gIxEJiBjf4Ro4yQsER20tf3xb4DYDiZ+RvtRqEfU/w3\nqOfQuuRTNhmi6gP5VRQ4YDwwvyzjqrSIpTxHupUOP/X4g598/IGFlZV3z50/c/6Dqwvz2UI+ntmf\nGpokoYU1UmvVb4AMfeH0177/SrX1p1Oj/aFGraqHYVHFwFcyopRJpNBuu9XlIbO1CW+r5QSiu4+L\npNTQ4kQh3UBUPnskYYCWxDmM+8/SZ7BD9kyxrzuGtGWQDhV2utKCIkvhx3fv3cNamYhNiJgwyNWW\ne+LktJi5CibWuHBBMhYC5fLS2v79g5dmskR3zgERZx1EGKOoAJ+UvI4OEjI3GOmTRoMbKxSEuQg3\nT9msWn5moTON7ewB72/nx17uvmxG8J9dBkx+hPO/uSt392TrzQ4ZkqAUx/bBob+w9PySv+k40b5Q\nTTB8KyrhlDuxa6qTl2z5ybpyMLC25e4sdxE7AkBxfWHZNA4zUVHaFjEBpYnMSqNTmNvocv112vK2\nHq15m/Omr3elRdy7dNnDqUH6Da0SiJpYDGQEeLFaBbEMMSEsrtLVYWx528c+9NkP338FuvHs7DNv\nLohBneHgD4kUJL8TzB/34eDBg+KFBqpJ2N1N4SiLqgfJd0RkaloKftxq+RekoO1tS8q2nL43MFfl\nhVbENVUOb7RhWA3cOHSHhA3HPAvvZUpmfgp0ly81GnjztJzimYEeyNcTk9B1KajtlTXRYNOn8559\nY3xjLtcYGBq8vojIGeG8PjSUwkwKkxx6EXwbyuGZDHWqKKmgHTI4mAJbNjzcp1IpTpiW/wB8M7Dt\n2n0ByVL3x13u5C1BZRsdaLfTkYKyoDu+jkd87NLPMXYWzvYHinqhqAxKij962ELzDUVWNzZT0SQk\nGMj/HON2IIZbujLzG/BbQd9qS2FTfjBuX4ZeDAqJjCAcBu8e9tXct3ultIW5twaFVpDh36nuzR8u\nlU6DatBFfKs9eSNNJ0UZSVeyxXi+ghgsrTvCE4xBEUGx0QEuAuCikJjqzRy8b/LwMfLG2LPPPf/c\n336F8cj/8E//2YmTd+chOrFhGPWD/9JiPn4thVZWUwlpBSrrkLpoQ51H7FeVWTpb5A/eFDFVOT9y\nGdJeRe0EnIzCi4ufkpbU0iWIhsJy+xi6TUyMJQXkK4Uy943ZE8oVVA3YV1UbRjhmA1QU2ypT1j1N\n/fWsIGmBKw6lGJZKg4mZMg36GFDEal1pl1lg2co1cahkzyTTKSjgqd50toDUWSyXLcRj0uSy1KGp\n0FamEnjQ7i3dMx3D7Gpy/0ji8b7egu/sF+SqdheXN8ndmdBtMWsCwrFmQFzN6ezSBKeJSnhalFl5\nd9BSGg7dqs3JofhwBrl3m9mddbM8TXaBuU30gIaskd0stqTxoDBLYL9Uw81vQ3XpKutaQu9AveG7\nfNe6bgUwDVYgaaduSuowz5qpF9YklUfnslUTKKESSsnmciJ4XSu7TWky4b+NVlQdUXrO+YRVzlU+\n8chdP/XJxxKpfira7z79V/ly7fRb73zh13+DPEYWjakAq4oDEq0rZA9wc61eq1u5er/y3JIJjMec\nTMYSOEBBtA+yyklY1aNOvggSWE4fpCRLlWpfX6xSzraa5RS6afHIQIapHi4Jw7rD3ZBWt5Mt+tqN\nHLoCUWyfDFyA5k1q3TnVulFtLyYAoMt02FDoFykMdH9dnwPyeBqG4k1LrcmIAJJgteJEI0lbtIds\nTSJy6lKEEQARf1JJmOmTttx2w0GdXR2ROKg6FgzP7RmYCVhfIBxqpwCHB8EC2bZcq6JRFRJ3X+9A\n052opuF0WRZ4v4URt8a5e0lL+/Bxm1uicJbtI0BVODe1CRFfYfOrD8ITqVoOJnahmosA4t5daq6k\nxnYVV84aZoVy1W4BnYlJDmPRQgNoyrAw4agrlxzeoqlewqSSYkTcbSup9dzo6rXSfcdvYwDebGZx\nCoslB3zsiqgbmN45I6W57WnCOUJLbskpgrO0qZxoldMO2USd8wJ8vh0mV4FxQ09dPs9zNGWHiPBN\nE3Uz6dI0IP00WnZTlS6A/9yIxgxxoczngQvTkQuno0YkjfhdodyKpaIzM1c51ob7Ms3aymAqWVxZ\noVvkKkcNFhbjwwZtD3UMScEaE7UAJCdreidwWcVibvEGwOBcPt+vz5qoopqy1nXa40vyaekI8gew\nN3opaF2t7c4uXaFxJ5dTMygdejMkbTALVLDHYJG3g49kcPnu6Affpb16i/ZIV4m5FcYct0uj2Lek\n9LsuHnlxp1PC3MF9Us+FjJs18rffloGhoULxhurKW2qD2ANDw8XVc6owc/xhasdbcLVXvccYd9TI\ntFRz1zaL166vrC2tJWJXpkfAcQG+DhWkr48WdJt9K8sYep9bUGtGl39tcW25qqob8UK+gEdsx3YU\nUtumvxpOhBVHTO117S7WbMbiYYU7s3vaznu+Q0Gwc+gPHNgnzPhOnz5thOODI+P3PPjQn/3Jn01M\nTh274y4CIaZqBDaY85Q1dqY/LEBumw5rHfQV4grw/6GSUJcwpUP3VD5muIWuizwkR1CmSi5LFdxi\nmEHCQEnKRXJ7tRYrA3nVg9c9MsefVqpmxdbBp6uDm6wk84d3o7tlH3devsElG/Rf9zXjdxjgd0J2\nf+jgSdtX+DSzHcuym01kb7Gft5Z7Z5+7qwju2o1iVpPJXLwwVw83RTu9XovZBiaeV9+Val1pCVlt\nSWHlS6aEjlzFb3I6QlIYIj9epFeX1mul1lvnZsled4VTmVgagJwngabfa1t2Kxr39Ejb0kje8MuK\n97dzvLDnP6Ub867onQhNp9HUaQwoHMgIUI5ILnQzQ5PxpHxUSiddcwydy1UK2Whf9JUzZx9//PGG\nW3399JknP/UUjWyojMtr62KEwI8sLFzXU0ZemmYtDZPDh6cJ4pbVT+WQSplZOK+W3d8Pa4HkiXGX\nkC34QZZ1qSRtGa3VofSgDY0m0CUsJ4Zf0fo9bF9LOohtcG/5+Ds9dY2b9Xq3J5FbklH651o3t/Pd\nCWC0vVS99Rr1iQ6ai7dF0gv4c/jgZufmhXDXwednvfZNrmS777b+ZCKJ0UUxHEoQTWnkAUHAsRY7\neITvlMSHV6y2b4pjBv0E1T8VuMDIUupFQkfuuO+nn/qJ3OpyXypZgEFcLo73jmrMjD88UmwE6I55\nz7oDWQ7X8efNuZLX2Wvqbq+IL0suRREGxFP7YwoISfQP1cjJdjXZKCS+D7yUtAHwvWT9bw8fopWZ\n7HdCiUPH7pq7sUbVuLGxdG1pg1Q6kui5eOl1RjAonqXRESZgozunUeBUDL4MgdLlEngwMxpVUzqK\nmaabNrpOFQ2+tmg/WDGxBgAso3LUDqlb3bzXkd6v3oI2NUFy3XaV0+1JxY62YTdfiMZ/y58usfmb\ndVR8FravmhGwwnO3+/jdtGJsmyF3PVTbMm+a/Gy7JO5zT1p8WUzF4qGK6ElYtN6ZElE9SXtRK3YH\n6NleWDc9JUrvS8INjJTrjffPXfjCF35tfb1QhfuRglo8hC60KeY5aqUquKbtqJMjiguGVVf7HEyr\nsI1k87dCVthXVXC12Z+k6opzqPqnIEQ0G6GlaraaSPCCbBbtmrZwPmofJbttMGoppqIfVqrN1ka+\ndOLuewnc1JAHbjs6NztDVxBk+wsvvhTCsEbh2oGasKbjIAFFqbUlPI/eXnHQBprOYB7SA/gw2D36\nQhWgylE31HPh8bsQftLsM3oCYGizywlt+3q62fL1heG7AbGBx9z1ma3V6XQNDo3tno/BRuQtUuEf\nGt39HnPQSMyP6B2rX9Gm0Iy66fvt7Kl7l2rZt9iBvuWbP84ENk7CqRYHbJViOhFlRiMEBfBhIlmo\n5Gq3oJEe4cOHJKuCVb6G2AjB8J0z7zFPxbsFjwyxd8JvA8a+lgsQCSERgW6p+kKZ/wh3uvMdWc1q\nybemC2qLR1RjUBSq65LMoJYYVYkQUxndhKgpgVQ+zxqoNxvBjqYTWEqOJX44tLyPHz/+wQcf/Jf/\n8l8+9sTj58+f37t37xMf/0TogQf3k5awjgtF4d1Aw5PZflQs2MMRuW4Eh9E1QNtf3kOrCqxXxTAh\nyWpKhG1rTLmhN58erLTnfIo13+mO1DbVcHY0Jd1JksXUG2l7MAuAPLuGL93J+k0iq+GbHWj21055\nS4eE/A89TIJr2nCDb9nqchZxfoxzydwJ3WBud3PYXsISWhKpeL0i/xS2IZ7lfSlUd5ti2Kkct00/\ncZFF3x4qmzrMi4qzihYQ8/nCxQsXAP7HIzIsFIsX8N7SWtliiAqNScVKVcMIx0xZ+3rdZ+mwweQO\ne4Wmn/XR1CuXRE+Tz5QrupEtI3CUe7Rvir5pGkgjJ4Dy6NtuDyGuWCE3gvh32Lp25dIelGt7kmTm\nDz744Ne//vWJiYkQ0FlVGURULKD3F6b5rUORsoYSx8qWHrQ6pih7acVDU5wqZJLfkCY9zT12pU7Q\naTkFhVbCtjaB8SAJ2uAlqIbVFa1v1pm52cG9vfTUi1gXSLpcdB2fEuoGBXp82ZLtjl/beV9djjo3\n++P7iTrKcMBvGlBjeeIBfldeH30379+bgTp1K4q3mrc4fLafeMo5PooeI1+j/66Y4+C90xvFZaNN\nUe04nYJQMcv7KmmObrbnS0Ukz7GeFueZUFioAqm409bK1UdWSwTvm6A/RKCloSCy8F0dW+exDGWb\ngtzcKmNc5Vj49rvv7tu3j7qxKHoQXIYom165PPPYRx5nxescWxyv6EXKOozqxnxbjUaKa92sRSKX\nQ0VT8zZXl7/wS58HEouoJ2sdepclBidhhgh1ncXp+bNei6KDBn1BZEtCatJkK0yVNthzFXyyIRMA\ndRhp8RaVXIaVn5eIy9GJYf7P8UuLnTeXL5RpoVKvik+m/GeKlLyp9ZwspZdqNZQuNWUjmjYiJAIm\nHi0LjDzVu+FLyh0awKOlQC8iZkfbytHDQI00UMcxzDp97PC6yNVERIEEF0hcy0sI1YVEOcOIiu6P\nPCbkMnlmTAKQxLOgs+LJymsgWInWQszMlYqJtMEthyMpCGgmHU4tnhCDI044Rnvra4u9vYDhqoza\nBhOhpO3UcmsDyZjZqETN1ulXXzblV9srq8v4ngO7FPUVSHVwA1gGrkDLW16fX5lomJY+bqSHzZAI\nvlZLfrV2yNH3Qf8n9DWls8XdaH9nU39Gf5VPlvON/bsPri3fqFaza6s3EvF0qWAeOfSAUQP9FG80\ns3aoGIqi216KGCT2Y94wVyAjYQIZVKOG5CdhJn+FGs424fPnr5SYdofjl69cyxUqy8sFNOWTiUwh\nDzA4WipiH9IHw2x9NT/QP3p9fqVSajL3ya3le2Lp+SsLPHYRA2lh7yqUbQ4KFgwiF7un95LXsS0z\n/cP8B5Ps9iN3TO7as7R0gyU3MIDEZ1QhnE016AQ9bumlKE349hSLW0SuRZkhPiZioyHlKMSjl19+\n9fwHZzfX1q0up5QtBfYf55D17bi2C3+CvWPi0xIbKkh9cQWnkWKOBItdSyGike7S+A9Ln0d4c9Lb\nsdHD0icgKo4It//QaWbgP/kzOAh1g+MbXa0KF8DmVK0rI5GGNE6X1EZJgmEj5Be2WbFU15tczCNq\nCGBVVFPCYLuXCpXR4Z5KyejvjVTKRUxTioUc/jSb65uc0JVqCc2W40d3cfIztkRp51/9/h/AP6QB\nsLi4mO7vo7sGkGN0NKbHSl1t+FtjgLssL4Mj2+3ThlskVzRn2r1q2hsiztnbnxFcgIyTTW1rqsvq\nukY+3aT25Xt4EdQ6tQgj8RsFRqImcZRcWfMVYYfxJT5ZVg548Jv37NlD3OTz3H8+5unjKAYOmW/Q\n/o9SXyqmMmFYh22uh5+F3sGPa+VeTbrQyQzfoGc+OrzyfDWkTCPm/Zum0wR+itfk11Gq2toxpsvk\n6Icu8e1goFvtB0/guikB3m1ppU2ONXV0xHgDtkJYsuaJnijU8WZ5O/rEYLUrkgt7o3Xz39GU/wyn\n679CoankOhKKam1otyhQrCDsoA4SWcVqLGZFk5FoguPRkK50+8RkgCIwEg6vaiUVjy5dX2nVq41q\nqy+dblSq48O9V2ev7N2NlHsJm/M3T7++tlr+7jPP5HObL7348qMffvy1N97EkYKFvra6we3+1Gc+\n/dzz7+k8p8t7bMd1H8ymgn2t7dZrwcz15svdEOqtWiiiqyHLwoUcDYtPtNwF4yUpnzK9QO6uueMD\nVXpGYXVLmkxwKPt4fLwmd4x8FwXWt8+cIWqjso0wpf6PMHN5Zgb4C2qVI1jWQFNSY0utef/ee+9d\nuHCBF2GJg3slh8FzhkXJhN5fu4QP/qml2ak6NHdHNzm0eg8ZPAnP7bffTl7OxtNqbUGHMz2o0lzT\nhx9+WFb8T3zhdzrCg9vV9dt5xNO54i1VpPrWYh07gavVCjDiuKv4o6qcdRUeSD0n19P1tj3NVP1S\nWt9L4Do+vXzH62kj+DwPPYVZ1Rw/Khv5ZhS02Ugii6cuoykZgpge809KcLURJacc6IdKwwpoFZVO\nNGcBtliYugDA37snjcvyyvImcqfnzp3lR9A7Y3AhwhvlMpoiSBODFAL/wxYeGZscHRtHDWrh+o3p\n3dPkrrwao2Wd0Jteouj6z6OtKu5sdf+23AX9/eBuKYrdcgi103I3wVdcOH9RpYDm4EA/4bInYT//\nd98mmpMXWAogJnNL3r7UXW6gonA9gVtDmn3y+LDJjsY+/+u/tr60pL2v0dtiydIGoftBvNeMbL0D\nWZ0k90Qcbg4hVgdybhrksldfffWJJ55499139yiLJWLNgQMH3njjDWCMrHIdtknl5TX707wOr6Ad\niak7OTZZ66zd5557jnWsAQsoBIKo1TInwc6vnuCGlZE812l/6ld/tyNmuOaPNdEMdE7MtlaRz3IQ\n0yBVm4vBmmno/qOj5sA2ja2IVkNrO/1qdLeWYl1f3wC9u7GBwKKoKdHy1+7SOy33rta15zVGOkSM\nENMoOgHK6JfOEky9OGk6qXe13JeW1+eI4Xf39YYL+Vq6BzPb5r69SadlYf+0srTBY56dvTw7u/js\ns6/wVLi/HK88VN4CD4ADmvtLcPqFX/js3r2H9+8fQR+k1nRTPWlWOSFtaXkFyVWSth5EPmoiUqmD\njefMoVqkprAL5K13nq1u51t1t/5ynK6TNtih2qExajahRVyemUXlhSWLoMVAf0+6J/q9733brRbB\nvfPcxIXdsjXE2wwgJ7TysO7/g2DiTiJsiLTOb/3ab1y6eAF3X5lIrqwxtCHKEps1c5JMhrfJ4iMk\nE3oXFhb4Nr5Bi7sQsPk2bh03kIqZaT3QXG4suG5+8K233uLVWJp8vw5wxWJeoyN5hPwKtg2HAxuG\njXTkyBF9M9lR+/fv18mMTy0K2Mw4SmclLZNa/4/PceyS6fgRkxkvVPsczba4LBWs5vVh/YXlBkkX\nRZoriAP5BskuSk4uW11fy68sb8Cn5o+y0cwKi14w/oby9LpF0m51/Nf+w0KvyDDCpLVKVQB5nkc7\nPJJAetx2Kn3J0PCAMdQfH0ibfT2osRm5LE4I+e9959svPX/ur7/8lQtn5zltufKlpZXJySkemPb3\n4SG99fbb7CA4spbQDuKPPPbRmblssdI4d3Gt6dr9mV4aIChwMH7gq6akyw7q2zofaCgPdVu7Utxk\ngXahDIIMt+3f8EN5gKIKbaAAlZbummPgRGKFkFGI9qT7DEdTWCzFR5cjzjJuKkjkUzT1A+Kh8Dfp\nNei3sxfOR+IxGKVJpDRTyU3clyLhYqW8kctif0WFcOHypczQ4LmLFxBPJMSKT7way3BDCCKEcMRd\ntMwY0USaiUx/RkbEf2Z0FPQhO4EPdJTRb1aDuNgSXAOvo50j+Fizanw4qh8I2H4cC5Ksdg3ef8Re\n8Hb9ky1LWMVAUFh5+ZNISs+VmmizWEHx1FWYoI31Gtfql20aWyH8dAsqt0CFWV7pNPMLDMgh4EVv\n2e22jK4oqAyfiOKWIJZN4frxEuihhNGnrh+YSkizyDI2lkpL12Yv5HBQrsxeu/rII486dRzLMmQs\nHKPECa6BO37vfQ8QbO5/4CFIgJ9IfmpgGA8tLqlx/MTx1Y384GAatGhdWej0ZgZ5ZvliHbo3tSAt\nAfInnsHI8ADQUbomWvHd6HTN9p30dgBHbA2XHGMnS+EufMEtNg9x8cbiCsurWK7KXq2XhkbG8ouX\nOOfwrhGRHhn1g+AL7XhQ6L0KhLWChKiBU02VZYoDGQ9xZGQMZTiETMhGCNW6rGQZULkSrcmnWQNq\nZh85ceIEf/emIDPktdKJrjuJ9HzbV77ylU9/+tMkKprWxB9CHmG7XMm3lWSabcql6uqqwpr3pTN7\nHhbpDWU0H/jjNh3jNYpJa7mFAihCjdMyb0072HHFB4oq5d4k+N6mLv7Ckd5YFOQZVs7XelIIePSD\nSJtfWU7EU+r7JdNQFCSIHdKZqVST+lXRruEqFXje0HyFm7Zk/L+9a7ZUqYpRTERsnsL2wGCM23vm\nzDxCFD1KaIYHsLK+MTI8NjQ0ctvhQ1C/E1Hx2IXPyw/ee++B+fmKIn0DIpLqLZkOLS6RgMaym5Lv\nczFIRSEys5kVITic0FGYWVriQM9AQRgcRjSqoR2a+MrmZkmbRfriPsEIbd08DwkMUBzf8cDayc/s\nlo/JVRaFaSVIJeo3tIqrxWpmcHAGge+miOaGxW+T7mmjI39qW1f4z1dqU3SBLFuTdbCI4RVp8/F0\nKF41z0HptUjYpv1y7NgxUmoSDzQGad2gOsgPrq+s3nvvvS+++CK1KZKM/BRLnAVANvLmm2/yJX5E\n+23wN6+sEfD+NMZn92nOENGEqwIGR/AmwPOBTt/bkjuuRoJpPxU5Un7qt/4X7cPBylNCkLhdVslz\n6KbxyWRKlMtjcdBF0CzAzNAzQqMirCzkxZ6AZ5zpTyr8NyMGcix3bhbR+/DMzLXdu8fgRNstbCOp\nb0zYgPhfIKZARMEWr68/MjSc7M8ILjoUdaOIHzso7zViSTubKyJ9TCtFPCGqlaFhQE4N28uzDIzW\n6OiwoPntkEmsVrU3FYmF3aGMGccDN0VDtzk2EB7oicxfulDbXPv+t75x4cx7v/8v/6A/HF29eu3g\n4b3Qv3gAu6en/+E//nvVunnh4iXaFAdvOxJNpuEYgiXaKMDkDJNr18RD1oXIXK3Rbg/7vZJ2n04D\nipgzCNOXXU3vm3qE3rdE5pYYSzl6KmQ6aM1ye+NKmw05IFdVctJxazQ93HabqaQ7jT4AWB19tsbW\napi+vgyv7Sr6123bLPnYa8f7f0ulDwg+HDn91hn08knwjhzYa9bKUad69o1XnUYhKk6dNQhCZJxN\nSyHWDY2WkUNFC+saal4uUC1w7q3myRN3Hj1+bGMzK/zXhrQirl9fQAYZqhBUnvn5a1wwS3F9fY00\nBKUXhqPYUHCxfB5LQwq0AUrmTD9vd3RsdHA4Q9UAHai3P10owZTAzbcRRprShbejRlaqCxkUA9PZ\nvC9Ww8eaQabVAIIKKMGBunyVYCYSLgpaCWaGt5RMJlZXc/19vSJ7VAKBGcnncKfgOdHfsJUNtITb\nXE4OF+rogYwImKiuUZ4cS6/Kvr50NisXJGkcR08oNjk9VCpp+FRrbLwnm2UiKxwl+r6ALkkPdBMw\nnxdxGMbJN27kdo33Im43c3Fxz+4xSnNScyxRp6dH1Dlv5zarB3f3uA10WPOUOB988N7uqenMQN/8\n3NXnn39+aGCQQxZzCAgwT3z8k7F4z8mTd9730CN7Dwn97/r1zYXri7NXS/FU/0OPfoRXBgfiiCSo\n9G0c18uRgkIsO2LUfhTgrmp0uEE6nxP4Y2kMTJAPHnAm6xr0bocD+dAa76e2RX0RuGy5vvQ2WCv8\neXpss683I1KbCmGp+S56L93s7bA8QpatuVfgaXWNKDJP0SgfcKuJ35yZbGk+5pO6baXbzUrNKqH4\nD3VfT49v8BhPjiOW2Z44lxrgq6RFrwefLbX9rt5sBHQLcEco049DXUsrXaFYPTe3OTzMUu8V5pti\nxI2NJUolaeotLEixPDk5wKrlvXHn+RFOSa2owcdkchSjpjlAq2twcGRzszk6isQFHtkx1AnCyl8V\nwl5pvbS0VFXFayyXk4MeAfLx8VHSX3ZjTyJKGrN4nUwjc+P6pvStJseyKJzQCDCte+4cWVuRh/Kf\n/sMfPvnkk995+uUjR47SG2E+Koo2rdb3n/kutxtL2/37D5I7YhPyqc88cvly8Wd/4anFRU6t2I11\nNW8y45N7D5cwW3Kw0bbE0aSl8FJqlQvauw2OdR13xxUfJIh04tK6VZM8oGv7Yx8T6glZ2lZA98DY\nciayLHMb8/oWeYu/3LvKWYlN+AKkqIXSQBWjEXsjm0sORIdGRg2ZlIugr3TMHKfD+KljY2vcdEvM\nr1G7Na0zZ86QS/joLhYPdaSeK+kTjNdhlbOsdfdQF47aRlyUnkTo3NHdRmmxOw09FtBLvNVyg8xu\njXjesZy4tTLPjkjV0Po6nip4NVFAiLAj01pFwl0lDWIBELA5rpcWV0xjjEegEm7NrhclEER0FfeU\nrU+OZSP4rlhRwIMx0LMlW7URS0BmmgyvVUMaudnoidnU7+De2BLwpsW5LmxOTKQQEVBCHbFiAcU5\nGt6ZeqU1PdkP7y4KxaQWxuPhyuL1M6+X33///aldE3098Zeef5Z48/6Zd7jXUHQ//vGPs75/5Vee\nKlWkeCiXXYx/x3clzl4oje9KXZjJc/Pnbqz0Dg2xV3kLhw9POfVow3XwzlFnX0j3TFQDzlMJ98re\nne7jjhSN4ILsJExZQZnfoHrWdgik/4PmLX/vTq33LUHgQGcG/IEM9WhRr2UL1Enrm7nJgfFUXz9W\nXdWGJCRYMyhDdv2rnR0HXkIDhkXqimnM2bNnFbFBqatapm51E5hIxP1RGqvfl0nU25u/Nf5KKy7p\nclP1BMPaa8nHF/luK6LPY0e6qp0geXKncLPzcte7iwlIbH4+rxEvKyt5fgGr4eBB0bYGPqOlPQX7\npvYluAUCOanzxMSgpnTIDIzcTdm6UyarlqOIo1cqSVrdyNnZwiEXlBykeELB6pLgP3t7Y8V8HaVd\nWZfMy/JGJp1SYPrW5Gj02WffeuyxO//9H/05yYkyxKrTvfrQw49cOn8BncfPfvozaOkLuCDdyyOM\nxCKKlyNvqVB2z1+kv2sODZMXmitr2XMXZnv7+p959rmTd95N6Tk6MXR+dhFpIe41anL0wpOppE5c\nOGY1zczyxNXdHXkkXat8p787a2jD13xsdQkQdOAizS6k148E4tiuS6PUr9zOreXh1Th+r6+ux5yo\nyBRLaWogRF7Mqg6pAPiafh/X9fGcndtMcCKu4EQoLvUEWmfVejHREtGFoxIlr+r0SW+JoMqIDu06\nkHsb2/KMl3UWrkSbbf8YRHZgx8nxln/8j5zPyHJfW+O4EfMW/P5Y6EePHlVzUBoj4l8wOEgzziAQ\naN0YV6YcSmBQ0nfHE8rRirtNIwE2yjGiLGuRxeefyAuX0lJWUtAYjUqjJ5UkdmDLVtigKRlJJ4xM\nH+kTO83OrUONKZOWcAJcOHtuZAAFseSrL7/IKIGJHWGbF/nUZ57avTvxJ3/yt3zy6JFdDKrJk67M\nbQ4NYeFUWmGUL6dqGgDW9eWV8+cunrzr7qvz1w7G4nefumdkePiVV04z9eCUGBseoRtah6GAvg7O\nJRWnjdAU/prTmftaARWxruxl+1r/ofJ3W87LN0FtdPS5b5m9tDEaW4fAlrFHh7AAujDS74vE4iIa\nGBUXYeYFlVpx19TuhcvvCdJ3y7XKuVkyo+O0pXirFDjEHS+3dh2dtLBSqd60wyPbwEf86qkn/6RN\nyQMSzYxSSVOI+Ck6Ksi+aDlInbXrBN4fAfkU+JvNJbotV2+y6PXr2B/5+X+SzW329feOjvVTRyvU\nTjHd24N9AI08JQzhahUA0vd4XAQzaM7wg0pwNKzes6HgYUyFRBGAI0jmR+oNS3O0XCHl4O2ihjfQ\nF2Ld0xtcXtoMm6Evf+krczPr3/rGN7iR/+r/+j9KCPg2G0dvP/LA/ffNzFx+6KEHP/Ppxx95+DDO\nzwAz4Q3Ge8KLy42jxw/GEr3VunERncjFlTdOv0tP8My77z3xsbtn51Z3TU2/dead0bEJgKdkq7Vq\nnTH16AgSxiggjKVS4emJwWjIhIOTiGGShwOtICml87FNH7RNsTO7MEVBFdjtAtaB6B5Iow0PDKzC\nmHTKDBXqJJjZYd9oMlBqdqiVe8N8d8flvjUGl37ltn1IR4xpWAsJt5Zxee6q8g11Du3f26zmmrX8\nB2deF312QXoKG18EHx3/cPJXldaKkVoChXbhsjrGkx97QhMyuIs8a+2niYA41ao+THT4161JHelZ\n5XxS16x6/XEaEGG5IX4UUHJ5lg+GkwOk0dw+QjZ+2JBu+x/PKmtiIkPiDu1atUSi4CJGRobVvRU/\nI/pA1NYOeXeIKFhX6sYicUFVjYE1G4ZaVi8L8HA0mHlRxr1qA1CLIEUdmb2wQa9qeDhjG9Hlxcq3\nvvXtdDLFeUUkSCeSpJVf+Pwv8f1//id/RCaD8eXKulzcA/eeEsOJuvHyy1dpXWf6B94/d37vvgPP\nv/DS7j376AzcdtuR9y9eArY/tF7tGxim7/366Xkmhame0JMf+zBnC6M4Bg44eKZSceL3jRtS9eJj\nDlVdpgF4E4hhoGCzE0m+oSZJp6s9LQJ8U9PwJUi7gsd2Xd9gEtMl76hMcbcG2BqUohsRFGl6bflK\nT/ro9mfgXbvr1iXa9n68WPSgvYI/SR8WhUkR7kBhg7VYb+DJaaiMnGaprXuZrZ3JhFoFUZBk6P/U\nK1wZbfUD+/azOvMCApdpGliAF154gdXMNJo7zOIGR8CXaGBo+RaeOG+KoK4WSYPP0zjnM+Bk+QYS\npF6xgu5jweusPTij6AKB+por28P5ze6PZ0W2sSlq3nwLNtYCrMeSFyg+S0EUGEO5BbzmDPLjUlmy\ncHrtblVKkHo5lF9f37dvPOci+StIw2TUiPYlr8wUsOyiBgAMyLwN0M8jD5145Qev3HffqYnJ3lbM\nXF6a+cQv//21tZWpqXuYbNtCa8K+xljepBkfXVhhM0nJBelEe31xtkS4G/j40QwN25cvXrrj2PH+\ndE8xt/mrf/9j+GLE7rldHZUab2PQrqS61TZPlWXxTSwKdd2gMtO+eypTlOqnUleU+0iYzrcl/dAu\nkwxxvzKMLcX1NjHE3DbQdYM0EdMTRtZeRW1GnKvXLt5mNC4SLI5Mr9gfgFvT8qWe+9IW58vWVPF2\nzqoxNpo9U9+xqNhSqu3EYNcjPSWqLHzhYrGRiDM7c3nq4F6jVATdMLnnsIHDOPxR8YItNhqFnkSs\nVHUCwDt9A1SSQzMLsFepyNyuaTT++M+/9PJrL/7Hf/eHt+3ZB+VobGLq/OXZobHJjXxhbGISDMzJ\nkyeJ3MR+etNiAMjBGg4zrl5aWlMnvw1GZmBgSOt063FSuwD1ZNi8GaoZ8vHdATrHVqlqtqWB2o1d\nI4ia1gmSrj8lmfnpf/h7IyPWyjLAnVghn830I7WVpek3Nhr+4P35QYRVLbOQL/T1ymRkZXklHu4d\nHYlmN439+3q/8fTrkXD8B8+9PDk5/dWvPkMXf3gks7h0oz+TWl1b6EmHL828T5R97MN3pPti1+Zz\nwyOpn/j0g6USzutDkGyqNWczW6O/OXNl7sDB8e99/7Vytf7s919Kpwffeecd+omvvfYaozhaMSsr\nm0qtqfjkk48SpPbuZXA9gMwvUHZXsE1CkaSPqdTlvZUXlGfrhBx0fD5oVb3DsHYHTJp5C/xcxycD\n2WZQ78BWRhpokLe5p5afw5udp7a1RfzbYnr7FgbBgBbcc111hQCG5OiQa8AdoJDPJxO0ZKKwkBIx\n67vf/67b5MgGGgm0pyHGui2r6+r1RIA8R6fjlpgVx0gRn/jox0hgOE9BAZCX08rjYV26dJEkBzgu\nO5PilSQR9AtZpfZpUgFeJGQSyrCN6lkEyi2zrcKi2Zu0OuqiKaDw4Uox3AqI9IhynIjHuY7/T1WO\nt9Ts2fCJsKpfUtG4MXEz14CCn/jV/5EJDjJMIyPYpYspz8BgT54oVHImJ5kfiTYVdcnQUDqZtPDM\neOPl85Hw0HN/98LY2G76lcoEQcRlBof6gTeAvBBEbas8OjZw5PaRaCyKos2NpZxpxVI9sWzOBQRK\ny5JfvbpK09sYGorli84PXnh+3/7b4ewcvm3f1avXx8bHUUWjpQ8K78679oyM7tq3fyQzwD/Be0Vm\nriwbJi+FI3YYdYSm4+k8an6Jz4i4GYbZ3BrlmJ1NdOPHWu76FW6hihOoBTqcxpSMZiPc7ksEl7sR\nCMx6hh/URm5Xrk43iivQ6Q8MqnxXD90RQusdYSIr05/Zt3c3sCunVUPd/+23XitvMsgQnpfWDmy5\nOy93JVJXIQ4SL0j/4Kz89m//NkNGp94AqUJ+wtoCCM2aO7B//5//+Z+TyUhbvSpVrOAsVMDWQHYR\nZN7c1LguNgwDSrJoLe8eEXKdth0XJjRC0NwoGQvL+MP1JZQYVqytr1VrLKG62HYBuQUSQ/cjCgWn\nrFtACpkS08M16ge9JOyf+s0v0pNLJpIE+N50L3BdZLyPHskUC/a775zF3xQFe7yzBwcG/vd/+e/2\n7z26urx4513jWKNdu7Yg7qmJyJ13HZibm9+7d/rgQfY50J9YJjPAGwDQPjo6FE0BLg8PDFtvnJ7F\ntX0jW/v60y9sbDZeff2tvfsOReLmZq6OhmO+lEdns2+g9/ixPcMjseGRSSj04xPj+QJvFSCNk82V\ne/tSm9nK4FAf5h35QqUnnWCOLQbeZhsvqz2xLLkd2ifP8Cbihv+f6bjBjmFQjfW/Mbr7Qdn/mr+K\n9T/byB8JSnZ7TzpGx4LuAH5trVqlIa5x/7axjWQUSGl2YIpoPo0M8NWh52DwLYpXLkvcmrtyYXl+\nhpsSC9tSSsCz9pRsupc7cTAalgEqZyhgAZJsIDFE7pUbiwRv3YXknwT+1ZWVU6dO6eEGA1U+z7LW\nDcqEuEM6mjPFUQPaka8q0w7ptquOiBAfQLPyT/pIuIbt3bNb3yh+nB3FSxXUHwK2Lz2pwbN8lWWd\nVp/XaYwuADTeXVcC9lO/9i/27UF1JgTuv1o2lm6sTYwNf/kvnoUWmOnDvG2As+Gdt8/umpjOZ8u7\np/Yke1ozs/PI8+4/MHbk9vGedKZUpPtBEmZcmRH4+JUry/jwSdfDtf/6r5758te++ZGP3r+yip6C\neH8vLa0CBz913+2TU/vByXDSDgxFR8YG0G46dFvm0sxSsxHBQXVjM0/+Y0jtxHi/CrQwkYw2FYKF\nVLtQrKbSPeyD3r647pf76Zrme3YqGnRH965kxuheaT9GdN+p/+UzB4wAxMZb7lomReNy9TCl5UHZ\nHcNz1XO3U7PbUHdXYaS61VWtgBibuQ0SLC0HW6ewADfrAuSSblsjEjbh7+Y2Vy998A71e1QKxDqH\nu2vuvNwlTDYFg5DilLfMbD77+//69wnnRw4eYuFy5wl1jEdAEEUUhY+6S9QEFJqXr1KY6vJ0cXGJ\nDyhnWYLEeNY6WDE+owFhvBvWOgIh6k2g11sr5osI2WJdTrJK2QWoNpHgEnp0o0tTqDUrWjlI07n3\nhOG1Up12hdFIB6kEnvrCF//w/2ftPaAsu84y0ZPPzaGqbuWqrs5d3a1uxVayZVvCcsSACYMZwGgY\nMB6Y+AZmveeBMawhLZiZt5jBGDBpGD9sjA3GkpOybIWW1OpuqXPurly3bo7nnvS+f+9zTp1761YH\no1KtVnV11Q3n7P3vP3zhs19MxEe+8Ddf27Z1x/zcwqmT5x5650Pz1+ZHR0a++52Xh4fHDh7Y1m65\nd921FdOJ7EASmjPQmC4UG/Bbhf0o7sLx4+fKJTyNCiezFSzoRFal6kfYvWv77ffcAwsNQA3wW5NT\nyanp4ZmZ4WRKSKVR+gj5QqtcbrIsDczlZpoYzhA2A6GbSjiisvN+MJ2DdCQhosN6BUGCxluwHm91\nMAn3HGZYu4NbQ7lsfONTmMWAy0y1qdtnlPM9JzP9mAB9khmf2GWxoSNlXKDJ8Tmf7Qrr5da6pqTg\nl2Si/+b8v4q99A4ppDi2EeSDXJ+n7/hHPHu73YyRITiUM9BBQ3VvHHn1RQxVaUeg4YDdJ/ZPZuBQ\nloglwC3GudQ0GgOZAdSdyNErBYKWILfBHUHQRccXiDBgGxHpsdwXFxZiTEiR5AAw1l1bg0scIjcq\nOqxCwNxxTciiVJZJlF2UUMfjT+TuWL6UnuiRZCoNioxKVoeKy4RbSQihQ3IIFl07HAx4f9hkqIaA\ncojVKkWDGMcW9xrjc1xsct4Vlb//Z/4TrPoeeXj32TMgC8LzIz05Obq8PN9u12Znp/fu3YKpE/rr\njPTDnMZgOyPpC3PVs2cu12vOt7/19MGDB1bIZZvIUWCywTKpUi2l0hlSEqYJsZTNyM2GsLS4nE4l\n8JO5XGxpqYSkC+rYA9kkiuPCWoVwqOB8wKfZMJnBExFBADgHchgNU4x4catw3bh9ZiwGs9L64GDS\nNDFD0cJNOlawi958u9+CVQRxk4Usvt25e3dsZsuduQoTHNw0OlwtyEtmQmtsPTaHsV8+tc917Z7B\nlhSWjN0go8d8X7j9HeKcspZfRTqC16KRW6wV1eXvvvAsClSR/KlM6slvKLS96A4hUTTIifWE1AJI\n1eYD9z8A1O7a8grWKwcpIKuhrrnrAnrOBUgkBsRlorkqallk7fhJdORwPuRyRGjCTmAm4xq2ChvD\nqkzz2wNyIxkHSIdUI6CzBNAmSPUqIiM0SkESJrccMDTJGtAWmf8uaFlubgimrRbOFjw4l9XgGGDP\nLeudP/wv9+7bfW1u7YMfugOO0JiSYSPNbB297cBEq40YZELl9cWXXigUVyanxhy3ffT1lWqlUyyA\nrWIyC8ohUDrRcH3ggQfuv396/23bBwZSAwNZlNfIVaDNtgLlhQbV0ROTGbKZHkiUK+UkMPARiSBo\nBii8hF1mfXoNlgqA5wGSUKk2IY4DPSmmhwF4sE5OOnTUUksMCgIwMgByFuk+WxhSwE3kGEOc+Lbd\nf7nLrriJFt+tLXdOMuw36ZQ2/J6X7fAbz5c76MdY+qzhJwa+PeHlzlShA7lgJ9g/AFT1UihdIfDD\nETe0n3G4s/4FHRzoxZRLZcxVwauWqb9oxaPq8898GyNy1wb/HwW05Ot+9S53T1cCCCeB0YhdYnx/\n8pOfhK4p8mlEa0RulsAkgAPmfRjwnvbOziLVQeDHWkdnHX9ywAwRTZgVAPIZUiRnRiN4EjLegucR\n+fuJHK3OjNA8XzBuBMalijiD2dfaFngNizgPxzGcJ/6JQR9EV4jHPUfLX/z0/4sMHi8dgjnIsrBj\njrx2cXQk99k/+kfL1JeXaodfeeuhd757fr6UTo1A/WVqW+L1Y8+946GDO3aPDQxEbr89A1Th7OzO\nbFa/fDkvyfFYQjh9bh62ukDUalHtytUr2NKZdBwKJJoaQaKPYqJexQvXkAoyFTSVDVVkBg+kvY13\nxdnc7CpLgYUGa2nzWjDgtrrQLhc8Y3KXKwZiBZGKjz+ZkATm9sjlbHD7LctzE5TYRJxlSkw9S+Zu\ne12pEV5Zj9aS3/pgqYgYhgZ4/ioEOae8iVPFWT/BS9y9M4fdGDioJFIp4o9y2xzBCQDu64MVf57F\n8e4uu9nAY3NVBeaaK3PwFhMolzmHOujEeTeYeQxqOtiGjUQyXm/WqvXq0ECOpS1KbmjouWefNcwG\n3G9l3YZiCKaBogen98YM7JMkawj+xDIxzOag0INU8hd+/hPL1+YkBkQT+XCBmXxVK7UY9pYOD4WK\nQursCtObhwwBYGExiE20yDgaKTWycMyVgKDUWCsSyzXCfEFkJnQjWzZvrXodrY0fkje9C45DWJeh\n4QPGCZp4WaT58DEGmp9xa8hPTfrHrz155Mibf/M3X15YLHzlK08BFDmUG8Bzz86CNWhDYu3a3CUs\ntne84zaYreJBa5XOP/vRDzeBGa7b6F6dOlkbGcYWVF979TQu4uf+9K+vXUH3CXx+AxcZOQwSuDbh\na/lpbnPfjo0KeOGZ/D/x4/oPwnFL62aDN+J6BpJ34T85gETodlzZRM9V6DsD5wlG+Of7Tgc3as/b\n3R9BhLvO8/IuLd9NnBKB0tBDIDsiIi561CA4orNx/avKdYR48ccl+FB6Iu+Fug7K3EQCrXRI+gAi\nQeRRtNiRn1Dnm8ILdPOQX+OQjoZFjQR/tNxtWNSr331LH7wfwLVrENngSUppAhPzoDz5+3/2/96z\nZzeiQC5HlQT6spVKaXFx9Z3v3JPJDg4MRJGujI+n83mYcYCBIQ8Paxcv1HND8XPn5r/59RcOHLjt\nf//V17KZQWgLgN6FHbyaL2Lav7qKogQtIXBGkziwgKVn4k/cskfkuIiems+jGPZmwzca67gb1orb\ng77qzt3lYBzdo8Da4x3nu75I/ZMcXiSEB/ue85brblYWBIubNw0C3s26xLTbDfHr/Vc3GKeH4psg\nrS8UR+ymDrMCF7Qgmr4x/C0iq4EGH2znUD+iZlNEewWGtMtXQZxnLwcno9zVwPK3G701tijxSDrl\nGIB2N3/0R390KBsvFPMAlkLbMZlAaGutrRUwimEpuMTdhlEzAHIlkx86OLFyOI4EyMcgAvYatrm3\nAHhkuHyYfcBWEQqBhkgWBBpeAkF6UPAh2SmslfbOqgcPzqJ/8uCD9wOaj/Y2OkilsosOydCQkEyB\nqCJMTsVrNeHq1fmXXl545JF7gUFHGrpndteFi5dSaTgaGBgrgDv78CP7gR9Dv2TXrrFSGbwBNTcs\nXrzYYap66KeSoRzONVXVbijW/D3E8jDwdXOF3oAAKoavrCT2KOSIYQJ1KJkRQ0anXarzN1AECCmz\nSgz+ysUkbH9dBj8Q/Ji4IbqHn8J76k1g8eH+Pe0C0eWCRDzVYT07i9uXgkv64tPNWrMGNJcekZ3r\nULz5onfoQaCyaLkmGNlZZoZXriJELgKEkxnIKmSViwWu8QPP9VQnJdc/asJSauEiZIMnhUcEu6X1\nwOYV3PzXNW2XLBPI90YplYlKq6DExF5dXiZy+MwM7KpJheyll45+8IMPfP7zT6CdBDwWLtM//+cf\nQy8FlSkcIBpNa7lSzQxEX375uZ/92R+/485tOAYZJTa6mm9BbxbdTzDeseNBUux0UjhKSAtAT7Ja\nTWFMdbnvOf49mLL3XdzXWXYhWwFv6XivxO1DNv8eXs/1AcD82R223HGdeWrR9/WHt2549QfKhD7d\nbl3YZ5PD3eVoBIQY9MrYUFJhCMFou1GZK62gjJMiJB9FZYVoXue68Tw5+Cv2EDRkhg/sQM0NxRSU\np9DhQD+RVYoJ8Mg8HFG3XWkPLUPwjUrfruuMC2F5oyWkWFbHAOZUVHUsRlbnJBNCqeiMjqTaLfOp\nJy/+1//63wCeYTo4DpIzvKuJiandu2fhTG12LMgHc609JHzZbBprHcrD0MbAOYibWCwWMGT99pPf\nAqztyJFXUXxmsgBFCNwQmUci7u2BpCjAu/UYznzPAf7m/dfD6SPL48VAL3ujis5muXsfzuhNGHsE\na5dH9x78cN+dv5GUKfWr2q5bM8gMSyKztJtKF3R6kFiTxO6lSxjlIPiReRuG5Jun7/w1U5LNzj2o\ndKA7DYmYe+69r9k2Zvfdtry6BslPiMxcm1/MFwomkdKJHEGa7xTiYXYAvTZzo0FDyOzkZlG+17vI\nAl9aAiGrJdjdOMyITmm2TXwqr7+28MYbRz75yY8MDqDVMDOcG4PoAPYoPj/+8Y8xxyXYMzEpXQkN\nbyGnqaD5WeRRKjz3zDHMihGwSYnl/vvn55a2bc9NTc5gA+/Ysfva1QXsDTw3ScZZwdHvWdl0i4N6\nvZfrs4NvKbpf3/emu6Xo9kya+sMKuj9YrdmVDnnoRfGm8i7uNCQxmsxG3Z6NX/OmUHib+dHd06Te\n7P3SGqUxqqUQLdXhMBKbyJPJqfG99dFsTO+gnVBagcALwlO2UTY2e/FE3kNPRlKCRwaSz6aeNwZY\naHHWsZ2Af8T3oUU1OGhzaRf0ztm18qnoghas5kAxk9M4+spl3mqOS0hr6l1yVBwrEiWatlJDjhCR\nn/jdV14+vGVmP54UZdwj33cb+p579kwwbp589QoSsiQ3Pf2d3/lfrZb8lS9/p1qxX3/txJkzczu3\n7x4dGb///j0ry61Dh6ZPn1qORIci0US11tkyPQRsM/q4uCHxuNoxgASkXcH4Hw43kg/FKk67cfot\n9xuUqqLQiwLnIILrN9SD7NzxBbS4oWSf5d5DWfIbkYEBZbgRybmbm5WqPDry39WY4hISSIs3VUS3\nZxBLuJr1xe0EyUxYxYDNYW3RDQqDPqUqhjIIcIAPcOl99Ezq1QYYCJgnGe3GlYtnJbFz9sybHaNO\n9FHornHA7YZSldIDhiNACxIkDzxgVCPj33/9i/8GotJf/OKXfvInf+qVVw5/61vfxo0GyQNtD87L\nJk92pvXiH+LKxg5M+AX3tGjE3hbCjXJ39GdlZnRP8w28fR23zOiYkPUkhfpP/OpvbJmZ2rk7sbC0\nnB2KRmJUyhtmmzwAZenUqbPgQf/JZ7+0a8e+eHRi987d2bS8tHAFWqGpZOSO23diQQM3f3Xu4paZ\naWAYh4chLkxqG9D6XZy/OjyYhd8Z+qmxhM6cpLg6O/3JuuEiaZA7hNRwBY7ukrrwHqHJJcsa+xzc\n+B0P/cPai3wZBI3CniDNLp/jy0p6QjFMjVUhIo/IEeqegbToK5SGExhJ9PIZxqqUe5rcBEUiA2i1\nWm8A4lZcW2NjF6AkdJv5qwDSkYhFW406GiXEWaSxEYGf0KXOr65BcwotQcRajGAkxsBlM1TPrpCN\nCFzyjaU5gsgzaQI/0wYXZJaacUYSewNeFKhB3Ye0CNAtwNTRbjcMrL1SpQJ1O9yI4bHh8cnRa1cu\nXrt4Dk69oJhx/9bAJU5iYw426cDY0qJnpi3PZoKQj202Pv7xn7xw6cLlq5fHJsb23bZv69aZP/+L\nP33j6JFD995Nws4ODJJK1RqwMWo8AZnsFnvZ4HdLTFTUZeMCkQ+eQsYnADkC6sPkWkkXQuzB+V3n\nUxYcTz+RpRCAieHlYiRM/wI80Md/5dOPP/H4zMwsukjnzy688fqVP/6jv3n4oXehfzo6Ii3Mt0ul\nWm4kfmXu9NiU7srVHVt3PfzwrvHxbbD8APgiGscBB34QxBPNnbuyFy8W33jj1LPPPr9z524AfYDm\nWcqv+bbfwSBT4PDrELBJ2jxjE7uY9n0k87qYPmxBbxrdg+XLp1ebCx2LG9HkPdGdb79goQchiql1\nyySmDSNnLUZEDbxfCzMaFSkEA3VWIEABLB1+E2rRMtmVU8GKeglNa+QDyKo9zQmvRduV6wYlDwfE\neqQHONe5rN/IdrvNgNw2+X85Bh9Emsx+1+dbM/0sOKzjStlwIcqvzl04dZxiIq2zkBxbnyEzH82t\n36Z//2//DUkL3nsvn19CzfGnf/qnwAn+gz/4gw7RO3Uu0M7b8ARjZMhetPKAXxSYSCqXzvOo3zaX\nTGM72Fsw0i3m7n2qncByXt73rsf2zt4BQ6l//MenLpy/NrvntvGxqfn5AlKpfL6Dmf+u3cNTW0Zz\nI9nJqWFBbNvotJjC+Qsrg0PD2DPnzy9cvnLtjjv3NJrOd75z7Nlnnt+5aw9x3eEI1WyPT4yC3sIQ\nYLrQbdrYw1DevDkjbsy2Ny73ni5+d/ordZ8Gfdb3xuRfCGUVXZWon8D0JDOBwgRgSuAeQcoC9sv4\nPZg24AVgHQKcXQcOFq5BqobpJtw7gIMA0g9d3w79Ux2/zUlYWB+Q+kEF6Q932Sc57tCTSWJwAIre\ny2GtJjINcmmZ++MnSl5tQjnSvBOvTGFzRR4LkIRAQotGEJQLEbfjyMsvaHCidiwvrdqw3Ne1X7qX\n06G77wJWCl0mTFdwTU68dQKCYUCPfexjHyusrT3xxOMQbAPQF70N7DEseiQ16Moz9wpiZ9eAeGxg\nUjnMzmTu9Ei9Izq1HFK5uklnjRsudw8qv+veX4hFBl568cgjjzy0a/f23Ehi1+zgtp2DibSUHYQW\nVBQbr1oxJ8fjjim/9J1ryEWOvHESIQqvb3Iy9cTXn8PkYnh0+sWXXnrwHe+4/Y47x6cG77p71/DI\nYCwxhCCOmRbzVJDofrByxDuCw41kV3BdYZPOzI1yd7e3MSIK0kZEbs/lCPZAoO18nejeJWHld7p5\ndN/Yk2FoCIHB6Qi9g/wC1CEEOBRzdHdrNXzHYODBkdEM4oLOIG4AVhjtdhaMPjp8ncWlFS5OFIKL\ncS1y4pYKHO/JIrnFwrhlk0Y9W98U5MMCILbkEPwfPqoyS2lZHxrdCOJI0IAZbPj2QCb+/JNf5+NX\n8UbLXexGUe/YthWhHQQg7FI2w4dyEWXtAAvu2b37fe97FMiZL37xi/g96EeQNHunvbA4h1QCA3sI\n6wEfjx7f0tICsr5AFcrvU4s3nbHfeLl7ugm/8nv/c2arsnP3JDipuGpGpxFBVq+jAV+CoTb1zQ0h\nN6j/zm9/QQQ0fWjqrRNHJqenAPM6cHDf2XPz7330nuzAWHpAv/Oubc2W2MTaJwA6EIvW+LgMceNM\nlgZsrDS2eOMvSHbDK6qvStY6M3Hz6B6sv/W6xxU3InLXc6ebgUOG/ir19vvWuwr8rgTlI98DaHsp\nTOoeel0WAcRFTB9hOWQYTZW07LHs4FReHxzIojNdrZRjOrLoOJTNLl28CBA5bj+YE8xfQOLXw+Y0\nNf/T5bkKHpo+sdYtvtB5gsPeLRUjjOOi0Kci6oRAIkgjjbegIagAP9PGL4E5BJi7bbYwGX36qW/g\nCwLHc8O9fss9dAHXQxWW+0/8xE/wO0s2NeMTiO6I9wCNMWRiBVQP6L1B1fCZZ54BgTWVJInTYqlQ\nrzVoiWO4hXFsKskyGbQNLSbbtt4rdl3nbVnuXoPh/Y/9AqSZ8RQQVmrU4f+rXLlUOPnmciFvunZs\n757MyjKuprKSn8cbKVcX9t92cGJicPfeKSAOkaJCfnB4VF1crtfq9uSUyvyrgAyTywBgNlzA05lD\nPN0RBsXEDhP53epy3nPFzTt3N47uXYk7Ow+7zVal7ty9i7nXn6gq9Jnk92wezkVgWez6pJCrz8ls\n9MjeKWxTKfnGqhrJJSuF8iBY5VE4KzhRVTl1/I2x3OCxo8cHshlcAuR7lXJlfGLCZB8WW8TcOInT\nM/kHik4scQK6sSYPP6S5BzujdMsS/8/XaQF+RGVACIXc2+hqUIsMyCkg1xUJBmnIs5Ix7chrL7eq\nBdbHs6+Tu/tzTidI4Rq1KvIWjGiAfAQG+NrVq6z0pwkuVn+UQqeOTIZNM9XPfe5z4FHs2TMLaQlM\nYZkOR5S5XVCqxV411dsEmGNFSF830u9tuXN8kfzhn/nPjbr55b97AsS8p5/6Lpgfa/kykGt33jl7\n/PhbopSChw802h99/07IcaWzSUWPwQoQBF4M49B1Q+4lyXhLsG1QFwENhsI3ah/q1kNQIWLB7c7g\nrTdmfezrvvOZRU9SHshyd+tfek2SflAUj+YfhFjBF5jvvkw9vhhOP96ddDPJjNAtARlG3YSqVdrO\nQEwg+MajEeTLKfhAa2qjUl2av3rt8qVL584tzV09/eaxqxcvpKBCmB2iWTXmO65TKBYAomq1W6Sv\nwiC7vPi0SWSB5eLURJZ4ViOy9aGwK0vFLsOmeIkvtWhE79NlkcUmaCdv6+DHieMJ+oxAXAKg3iOq\nePXSmdXFa+w0s/ou93UBwHXlGfoo5Fc/9alPga7KJHUjMttxzBIL0BKCZllE9qP5McgcH/zgB48f\nPfHlL/899vNDD70L4sCYc+GQQW7Lty0WD36d4cYo0jskyK2+XdGdXvPuQ/+pWVf2zR5amF/FE7tC\n+wd+aN/AEIG+du4eg8Q5uTiKbn7VqpQN4MvqoANmQClC+EFDxuDnUaVWtYhyGx8YAHCgmUjFUJk5\nzBecbIwVT1IKsDxPmVJReV4apM4B377LdVpcf/GbLndXCKRGww2TUInTXZU6zkYZgqCW6Fuqdudd\n6+VpYEEcQCyZzxtRh4CIw9gFzYYzp0/Mz8+dPH782NEjW6YmG+USTJm3bZmO6uqhO+5wMMBTow1m\noIX+xlAu57KznKhcErlt8vfHn9Fmf4Wdl+x9MGgv2uAyv77U4pPXVcokv6tjUbuTFjeTgAuWuwnG\nkBXR8QAuHHKXF69duXCG5Y6dzZa7EAhZim7gbge02Yc+9CGYgd13332vvvrq+NgYVoX3rzQ8sniY\nR9bOnAnjH/tnP5lKph9//PEnn3wKZKh9+/ZWa+QCQuaToA6xCO/680am5aS8Xcudvv6jV1vsxKHp\nHngYKDJ4/5g1wsRuWru4CRRECkTViBUe6ieyfqrCIlMXiAq/xEfonFfuOyB0IePCDx6eerrdQ0Q5\nNC0Kp/u4xDhGEVwQwGAxgMqP61opLopm2gxwfq5UDN4hNZnjnBbB9MRl2uoCkwyHf5UREzAUFIrF\nZiIJ1ptQa9D3mUYP9rEYT2jUb6V8VJifX5ycHFcqLSiGFvJr6EIk47Au0XGPUckdPHA72Z0SU0cm\nT1e+20H6bJJ6I6nJyQpfGQiNaGJI3QWJIvplj2SGr7BIghO+frltCr4Ps6fej3xaybtIqeyk5qbw\nfK5tuGITjNCFlflMMq0rMTDndaEzf+nYX//l/4C8WlJU207VEnBKm0qUAiwwf2jYRCMpq61iNIn7\nkSA7WsBr6xKpIQp//uefHR/bYrTdgezIhfNXoHB4/sLpO+86CO3Pjtms1aow8AHZlHpBigJyMyav\nuDif+V9/iO0BVusPfOQj+BUyNVBUvHeM3lKJJO4XOKwYV1WqLfamVHLqFRhrx+UmXz7mWeSDFIfT\nGh1T3DirWp+Ff//P/yo7lKVgtYRE4PtUjZs1T8K/En4mHw7ROyHqnodfR9hSDEG7xBCe0ftT6mci\nIvh+VPgRPsIE5AE/y6gv2M0wK0YnWmBdDiJ80MyD3KVFsObB9AH2G+0UPnaGUoSky5khtVSBOj0M\nAwF+jhLuRBCzSfWtoycncsNf/cKXFMt9+mvfmBgciSaSuPCReHx8Yhr2NeMTk6lMNp7K4vvovcGM\nF1oC5GbqMgNAG5auaFcDYNcOdFQQINAzYFNAmYPzFe6yzv5qUfMkhIvsEnp3wiry/Gtqrju6LEQk\nlxqNmPvA9dCR2yv5RQhpKMSTBM0CrSHpO88/7rhVwwUZAk4qGq4SXT0JNn2pTGrYNACqgSwFNdpq\nnQp+TI6JHQmMaOFHfuTH9u27E1krDg9MG7EXxsdHEDBVYgtJ6DjBRSUCIFZmKBZJohzPr6xC+QLW\nNEDRQhX0heefh9reXXfdha4O9wUplUsI8xAawmg2GkswnjXJE2CUy3ke68Wet9YFb3RIxbrcs9aD\nwTnl7j/4rz7NCVGs8em5goQlYEMN8ust941FZzdBQfQZx55cChZYUOQFxXe/ukTcSI/oapU4bj85\nAIFTh8gyktERIMDEBaUkYvHCO1fAuonG0bvA104sQkcQxo4SuaNZSKmBbwXBzWi2o9mIYbWRHQ/l\nYPitYBFeOH/xzWNHkR+cOn7SqNVXrs7vmJ6BJ28mnsSirriKjTm8rGcHcyBaxZIZUn7So66ioh1v\n0VqX8In+NqCKNIGi9a3yET3PUTiLHv0THnc8izgf04aX3V2ph5Fkbg92jR0LSGVkAW13F3Qt03Fb\nrmyAJ0QCgSLqqyTuSaNejCeE559/QpDNVK4oQVHGaLWbOEgSipPq1DFDXIXGWDrbFCCSJ1XiWdkU\nVaOpqfEZq13avm32gfuglmXQTqjXweyr1cuNehlvCyIf6LTGI0ldi6M51Kg04ymSyMNphgBP2fwH\nPoDDDapj6Nvs2LUTByiXD4DSUa1eg8kHVD4DUgsZNtJpjE5um9aP6G4opgnfv3GtrwMW/uJNN6DD\nMBkD0TNhk6QNDRNJ2GB8Fc43ODumh6Pk59DrPj+86sLuZ00bm2NE+yLgepKZUPYcegpPNiiMplrH\nrMYoVBPqGMV3MglimFCo2XzGxgn8CjsWIf/skv2O0qp30inwwQniYHUcspey60899RSEkY+9cRSd\n49MnTh88cAC02Wa9CQFhRKDSWmnL1DQzCUQiqy7bKs/rkItzfRUvqQgZUoviupCp5BgeSd6vQPhG\ndW0nPE2V/H4rBOvC10dy14UUxZDSXdDqhROzDfiTrTHYI25ew1E6cFBdySOGNlKxwRRATpqT1Bu/\n+9v/oZ6/KIvVBx6Y+ciHHzx0z/aZaZDp4d8kNuvCuVNrf/eVZ5985sjVpQZeQTSj6FAFXW1BU+LO\nO+969oVnvvPUS3iFA1mYpDahGoZMRmLbz2gZNioRETmhbjQ6kazM4w53/eUeHvj45V/+ZeQzAN/D\n7xdNTMwoVpeXEf6R7cC8i0syEdmf9j8FAqArNy7OgKgeTgHCjAX5I5/4tTAoKjwmDPc0Nifer3Oc\nN45vwi3zYLnz9RqGdAfnRr/GU1cy40/R19+MuIn3NFICvtnQgxAZfRi/Dn5JMqUQl0xSwJqvlJsx\nWPKJ5MGCFZxJKvGYfOrEZYgELs0tIsAdP3bs4NZtF0+fHRsYtprGPXfcjYlONpVZXFzZf/Dg2NQW\nqDvrqXTZaKvwg4D1FGUPUbbK5AZ8dkCzN030X3FBcbgwdqzETKZYQ4X9CY1kXA98KfjHnEXoGtF1\nupa74Hfe+RxiPTT4JyO7FK6wQQ8aVB4aPVFEITlgG6c/tUHgKduUBITanOooUSB3jMJETt+xbfRL\nf/nYR96/f8cWOxWbT8XmkpFrRvNEcfX1sVznw++76xP/8od/6Rd+/D3vuGNt6dq5t1YGkpQ+oLPy\niZ/9Ofh0wnUVM2MwWS9fupJmyB9qT4G87OIKuwgdzVa7XMmDIIvEBFcBMjVY0EAfoHXz2GOPIXVB\njIdSIkIDBFZxnVDEr0IuFJdXUyBdJhNAy2Chmc+aHWF9lOIvVKfXmjPQ3aYl+tnX2kG2x3NoXj6y\nmuAWStVgxOObCbvdKdT6yg9kHHumqkzh0dmsVA2+7pWd6AN/9d5FmwSLeXogQbjGO8Qs8Kp0/NP4\neOrKpfzkZA5lJzToz5+fv3zxIo5RiGMhskKYEoEHQX3u5AXC9+eGkAPBFjSVSct6BJkHYuVqsWIg\nk5aUZDoFk0GLoQCUtsTxvbiL+C1MyLmeDP+TJuOuEEQFfN00qp5gp+P6+5OKbOaHuv5mxXCcD8Fo\nJNcruRAvOSPSCdGjSGE4CpljpGj4R4WdhYA2WCKI1YYLC8ckErt2JRUpp6Mr+/bomWRHdX8zoqcl\nJ2ZhO9jwB5ejcejBV0q1a2oEdY5WKODHDu3d88MXzzh/+tmv/M8v/C2e7sLZY089+Z2P/tDHvvXN\npzByQJfm8Ksvt1p1FKkwoKQRkgWBWyQoUMmLcENgvE5EdzL8iJJYKSZTwJBD0uLxrz8BN21E90ce\neQSOLAtXL/EGBtcqo/YDcPlcrcCVPFCN68HY6O37Vp49FZ2n1IDlHlqXXfrlYcP4ntXWd0X6dkLM\n+CC0wHlg7klINriKCpxPGcZIbJbMhDMWyRU2kL4kfvt5mgQWpm17oDqQUaqL5sSEevJkHpcPHkNI\nHE+ePAlQB0D5e/duO3z4+L13H/zmN59573sfPnv2Av41lhzBa0fnCi6CaMuWK1YkrmDkjOwM41Bs\n0IEhfWGhgokbng70ZIds23R0XPFe4skY17Uie0G6GywKMClPvFuedrdI783A3XVYVsb9LdCgsEyz\nC+Zg+0mLJIbdLCTXCTSbyJncD2O8Q0DbOwJtMKRMMJFQCRRrI9i3UZijEXT+xKl0VN42qu3aYk+N\n5AX7RLV8dmZwiXjcpPECAwRg02FGCxuCKtYoexcoKRKSGK9VLF1LbZ3ZsdC699A9Hzt8+IlXXnpr\n+8xBF0IDLbfeoLdQqKwhrRsdG260SDAVLVo8clInDy9cIlDBkc/gzWLp20yljJoKESBqB7/whS98\n6UtfAvoAfNPf/PSnuOAeidJEyVg4mUjjcRBe/IUury932v5mj9tHV0X3Q7/466G8wksfuQpzT2eG\n5l3X7czwMskbZ3s4QSHomvc1V/BPakkUhesL6rI3IAR6G8GBpUhSOMvyUyNIy8MrSiaReEM4c+Yc\nFC1XVwtgh373m08lY8NvHTuO1p7ZNibGxivF0r33HGrV4WBpMBNCAf1gJIq4Q3gLBUFzdWEJGmkg\ntLtCpYnLTHceBhgqgarIABA5SgpuUmm1XunENTi0qYA2AhdnkXy7DGEGtHrR5BZZ3xD9QokN28gF\nBfdGkXl0555nPLoT+YPZgoaMhL33K0pdQUf00SxcWzi4QUF7zRBpwgvtOhTDhA9DaCcUDTwq2o3q\nyu5t2d1b1Yh0Ppe9Ui0/H49ddY0mBSdRsx29VhcLZacOG2cp7YhR8l0l7DaEa0qqVpbl5VLprWp7\n98///I8tLSzdfttdsWhGlqJT41uhqDEKd0XI7QMMlEpguWO+LkdkwzKctoNVDtwY6lTEcrxxGKlG\n4zG+oFHpIuSjRrr/gQcgi4s98N9//3excwCxRCOYSxvwKbOfBUj+n4EgaK/OfbiYkT/y2H/EjhjK\nRor5IhyW4gD02RaSMESGATiRUrbkoq1cKTfI5gRXizFofP1RHkk9jyH2yYXKuR43fUdxxUDmhQVw\nR/S1SjttiHPgMaU4mr8GrWW8EbkjR0ngCguD1gY0nohBaVFpiwdXSagWrqCNKLxuIDZvuiWrpsag\nky4m0tC4kbIp4A/t+UvnTh9/8+tfeXwgnszEdDhKAjGYS2UGEslMnCZ/p8+c2rlzB1TW4un07r2z\nLdvVk1kxlnSjyQ7kUASlKal1R27JGkpJ9Cw1wm5AURvSinjlYAZB0xS4agcYgWgErH4INwJr5UB4\nETNBTOAIrsKqMxw+aCi6lDNTZ0Ti+Tu9P3btPHYZpEOjHGpB8EkqmqEKaDocOccutEDeCpR0L8TT\nZiSGeK2iz1OpZXG/mo04KQsoSlQvgj+vRCPJXL0BNQ1gLodjhdWBhG4J9ZpbceKRuqC3GnpaHYy2\n65Pa4p1Tq/snr2idV0urJwFYbjfislpFJ8kwxVZH1PXB6al927fdMTWxf2Jsfzw67lgxgA/ASCOa\nDgpgCAvbh+vFo4mIvJJv2PLAm+eupUZzK8X5pZXL4yPZ1186HFViayslFJii6qDuV6UYuNsQIVN1\nIFDs0fFRkvAlgeI4GUrDFpN8s1q5wcHbDxwYHxt1ROXo8ePPPPcC1PP27rsNx+lqfg0mc+gCoSgi\naHMHDHcCB1GnmdSVDQYmwtZ0FVkNMFp8Eif/2C/9FopdHK3Yc+mUPjQkmjBbrRr4+k/++P9Aph7B\nBiLUO3eOQq2GsXXkXhq5G8Zg9VaNkt8r44YnFIFY0QSZA0D+W1AHVmWwnwAHRf8bWiSomxZWC3oy\nhm4e4hE8qiGwg3srU+Oc3FsjOrTnIS/sVOutRFxPaZGFi1ey8cTXv/y1ZrHx+JcfP3X8xFPfeOrA\n3gODmaHpyZl2A3mBPTw4AsUosCAS6UwKsOZUenJmykA7EIsb/6MRpsBqH1KZtInu5tDUC6hGOAoz\nuFLgrUWVpiQHH1JXzS1KghsWaO/i+4Woruw3mX85czLkErVhTY51uX4fvMofZMhcjTXLWr2cRool\nCMloHBiaFjQ0bAukHFA0ImAFNtfcRj6ttVW7mIoP40JFY2k9kinkq3EpOpaKl5dO75q092y10smr\npeLhpnEplrRh4CxpjmVUQLGPIlFLpKHCMjA4EE3EMMgvrC3WG/l2u2LbDUQqJMNMkhi4MmN4bGu5\n5s4tFcYmtqpaDMrapGXU7qSTKWReg0PpRCaOHAiOQ4COK2z6wUeZCO3M3w6alXEufcO7rtxpAwkP\nksn7H7gPf8XY9fDhVwDL2bF9G8cSY1m2Wm1oVg8ODjEUFu0ZfB97B/cHACRcXd4C4ugmngJARezT\nsHB5663zeK6Ll5f+8DP/XyIOZCZODfh2qEDn4Z4z0bMsNo9FnQG5D0wrRHHoAoryq8LUzlhRQeBc\n5tPr1MhVg85xpAQoZNAEpC4CXMpMc2g0gddeb7UBBwfwBjQfmqKZTjopDw/Bsg+qsJjD62dOXH3j\nyNGH79q2eq106dTZTrXZqtTvvv0e27Cnx2fGRqcmxqbjiUy1hm7XYG4YXXBR0zEk1R1FiiYzKLza\nJggzMlCcqg5JIIRTm8/w8TJJlZBm9LTKZA+XQlp8isjFx/iQ3Eec+Zkitc9lKYyVDZvbSN3Ifs8j\nmwBjNk2WOa2BVr/tu2DzXEWQ+Bfsc9RtIjBIMFvSEh1HM+VYQ9CrQK1H4iZ+EJ3piG6YLQQ1jCbr\nrWql3exAgJXyeAFjHxXdo87KQGRtOLmUiV92zJOyuDgwCDKXVaw0REmPaUQ8pXkFOQK0atXSWn5+\naeFCq11otYu2VUN+hA6PwBY7M5aDyY8MHyMMnCyXimzQnZt1KxFPYxCKqTMiejIdhTIF8O2CE5PI\nWqXD9eB57o51b7JGDQcO8nSO21ASU0LXqXngkpET+gff/tY38bv33HMP2vZ4/nIRmuclrlyED9gu\ntYhmIAQtSAaJk73eLlbYtvs/cebs5V27Z4ulyo7tU0jatm/fubi8hID1gQ/ug40UNmAasq442zgg\nU9jAxnDDRHoh9CdDorGF7t0rDmFl5DCkvooqYmpDt4GhyvCPDB3FrGMdp1WvzUxnS/nq+FB2Zlwp\nLTeXry2fOnausLi0bWrqU//x1x/7qR9+4qvfNCru6ROn9u7Zi4HovYfuhybw3ttuH5+aicRTciQO\nBhjs3qOpOCYtNcONJLUGBpltswE9YdA1KbhiCagcQe7BnhjWilovoG3KIkcWMkiKEODyBderNry2\nru1wRT6JHmG9vpfEXiJVKBX3HCAlRfJvzPo8eyO7fN3/A64ncqylpdpqsmCINTRVScOIJIvQBcRc\nDBJujpxwI0OGOlDAnChZURKRKsyGzE4mGXc7pYRcOHQQuMxLonWmVb8AcxbgcMw2sGRowk86dgWb\nhhqzhO6C+0UT/CrgBZBa454AnYC1znXpmXwNoTEqtYogdTKDMTQZwdaIR7NAMUNKDApOckSoNgqA\nlBst/AJ6vglZbSIWY86NORZmrQ1/qIw+I/fhIMwySdE7TPmrjVQHMIT3vOc9yPWx+keGRy5fvvLc\nc8/v27cfQ49YBLp8sBZFqZZEAgMTJLiBY2Fjw/h6qArnXnmH6sFH/wUqACrDgWmIRl58+eUH37F/\n61aoFWeXVmiaCLMNyI9BGA1VBItQ8mal6iaYHYcDqARmP8nOAZEUxSzaJ+jFCnR8wCaFtDuwzoDH\nAPNHE8Ttk/EoMoO2YjWMP/vDzye16F//+V++89CD7Xpz+9R0YaWgiJGh7EB2dGRmxy41Hr/trtm6\nKSYGBxF8pIgiwlzNdCzAMDE8soRqB9kcXUuidaqI6ETZBHEMDcRUSu2YLmwxUVZSFsjnPS4H+jjc\nlM/ve3N5SZcFddYF545Q7Ds8VWOQG7cHaObJR4bGewFSH/hyBEr0qkn7h1lVeZGePSd3nOJfM/KS\nUxLEJrjGpJOEBdqIuI2JiKnlzyUKF8asQqK0NBOP7BgZr63Vi2utwcwITACMhqgj8GlpCLHGhGom\nWnA7Z2XnoqYsxfSGY1YRwnEP0D7vtKvU+RF4Gkay4djwKrEQcb9AM3Ukz6hY4JkXegxQtI0lo9Bh\nlyUL8EpgYuEDMDo6BdhsyzRosUgg70KjTO+0HHBhJc3zrguSQ/5FGNXH9As0nnPjn5G9AC28bds2\nwOWXl5a4ejUGsZDVHshkd+/eXSisgiCCzg/CRUSPExaJ4KLcr4o7yyLZMQmF/lt/9odDuanZvYlW\nG5YB0jvfOQswyUoefgEKHJHQqYAHARqmqVTU8bIupRejEmIPbURxsUXDTxebrxliyApMVpMpt6fT\nqmuKcJLAMCQRk13MNWOR86fO/8MXv762VPva3/1Do1IbHxnNpgZADB8bn8QWXS0WH33fg/lS68Ad\nuwcn01I0tlqqWVK0CcFjXcMMcbVaN3AnAPoDfUEUa606hunxJCSFTXTsEnHCEqJvgyuCnBedykD/\nQHJDHHxfw8oL4b5diodLcfx2EsOae9pwTBgwrJIQxHKu6CuEbP147g6TB47o4ppePHEPW+/2zIxx\n1EsODqaWJjQyUj1nr02YC5VXvhq7+PyP785m544c++JnOmdf25MQdyfdoVZesgantMwIys5qNdbO\nj8dro+liTJl3rCudDrSDMPkxKmhENMuWXTbtoigmmb8sNXgd0jDogPJjUnTQiEjgd1AZ78Sf9LDz\nG4hNVIky9X9kMrgdykHMCMmO42pMTRXTWWh84xy0eLDgfADmLGIzlB6B45kxtRFYLyE2Ay+J6D46\nMsYpgt/3yKPZzMDc3HwyAfek2KuHD1+6dOHue+6EbPz8wjUs90YdtFcb5wYuJ7t1YNCL/GvEOvld\nP/6fcScWF2to9OB9La8gJkooe5EbTE9n0HVjeClg9IDU01lR6/aV7gnA4UKvubjDTaNItR1ILWaw\njfZvNqk7HXdoQC7lSU4WZPYE2qqyujy3/K9/6d/u2L59cmLqwx+699z5pbvuvufE6bP7DhwY2zJN\nJIhkamhqcK0uNAWn3HFWV3F+drLDA6aLRgFweqSaJTMXZpW9S9wcXRbx0HEdqCdAAwwsc1CNCOiN\nXgrArxbmgtDSsVwuLc1gi7LEbW+gBuRIPqWKp9+y6OdwAUE+ZL7ahdAIoTXXeVnrfDwW9R2LF2e8\nN8/XPS/meuaC/BdhaYIIiRqBgIGipNlG1jHmXn2mc+Y159wrndMvzkbqu2PN6slnqiefHqqdFWvF\ndOnshLWgr72x/Obft/PPj6XzuUzDaJVASRCE3MgwGJfvH5vYW28J6OeAy0cNIiYpTKUAMnkYyyvg\nWxGzD0ckV/dgy52BTWS1XKkl9AzsEZrVNmAUkZi+sLyYG5tQI1lEMCTnWLd42IgGRGrNtFV+Nfjc\nh49H+PvlHhucsMutZjgsDpiCfB6gHYtwB40mJiR33nkn+Q87NjA5WOVPPvltJPnwGSiW8oQ4RgeI\nHpxc+Bhlj24WOvVoC8o/9K8+xZrIQJVQGx/RA3kVy3sk2POirsVtyGSUYrGBAAfOpWn2ukd0M//F\nnqlnjJrTZNsJhHcSkmMRasaBpbMwt/Lm8eOamvzHf/h7oP+ef+a52/bvz6S14aHUwdvv3bt3Xyye\nmJsvHbrvHgBzb79rfyyrz+crrqZgMF1otqW4BmgVYvlABGxauINo5QoUyp1UUjdaBNFIxfVkHEgY\nAMTlTJQSJMfoJPDedEiAA6OnkvtH28ik4SJY9oiMnpK+GAYpyJLiuV/JHkKfY+v8YWevT3yXgK2f\nxvBGmNQNjXY85VsyJKKzjml8g6aNL1hfWeLFjujvKzbGcJsNTVAzlpapubGmg6sZHUhmVi5f1Oql\ntN2Qyot6uxiz1ihpUapK45pZPdaee/4HPnrH3u/fbRz7QjX/8s6d8Fy5qmrxlWXhc597+o8+891y\nKTk0tL9jZdrtpK4vUfpG6gkCin50CFw2MDAxrTKpOhV4Y5nUwMkiod5qRNSE5Or1YiuTzOKsKNdK\nQNJVm46oDSgasqloIgJH23I8hlCTd8U0YwWQ9xh3ykYw5b49HLbNPHqTHOJL3UPJRTsO3RuEcwJI\nEw8L/hoR1K/QMqhVKlu2TCPbeeaZp48eO7J//97BgRx58jQA6TBoYWsajif89ey508jsxT95w+bN\nL0LkSYCAw/01ztTygMNWKsU2I1ZzFpKTSEhza5Xp6fTVq+VcLoNzmLYggb2IBU9zxHgMVoZ4lRlQ\nQAw3Hqd4gGsD16f8UuXiuYuVtfJgamDr5JZ6rQbPEfD28US54aEOYdxwCNad4VFWSaNlQScm/A06\njKlGW5+NJS3O2PSXVsTX8PBDr7eouIC/5PbK+/tRU+yWYu0e5briej7mdNkIe9xhd51iK3TLK/ju\nIM46/YdNjcNm56JPj6Dpr1UPjfYk32nD5SkNTnW+WwLFMjOrOsv1ETcJDcSlTknIOmm5FD95+MTv\n/cajGWVAqS2YxeS2IUx8hHxnVEpXjAr0T6GZvlxZiI8nylp750MPWKOTx1et/+s3/zaSygI8B3Og\nb331v1888Y2oVpGiFW80oLDGMb1USuiQHiA6cMd3lY2QqXVI3R6R3XxW71DXls1OLEgND7zzwZ8q\nlFIRfboEh+oE3FirkgrYXaJXCE3oAVB1GZTbtNtYkeOVOiInOZCbSzKB9P25558ndxrXAcIMhcOB\nAwcAYcBoFq0b3uHhzvS4hsiF5B/85K879B4Umms4XKqTiL+oTWu19mAusrxSGMzFajjqROiimCOj\niVLRoBkKNJlkRCNThiOG7aZiWjalthvO1AQmVu2Epn/h//xtcbXaXDW+8/TLVtM+/uob73rgIWjs\nbN++Y2l1ZXrbtmgqFR/KyJl4NKdjsiKlIlY8Qs12UojAPEsgmC4HJHCFIda+wZtnFGPqCaKw1FWv\nFx4om3LIpz8a6O1s9LC8+5K+u9BBbv9J7zqIv1tKUvByGSeM3CAQmCyHb2VodmEGZU8Ire67crth\ngycae0NYPwavZUdFP9eKKIbYka3WpCYuHX5ZLMIOKFK16jsP7IVDr1FsNItVS0YtAytmWHZokVSi\nanUGpqdbSuz3P/PFugnETicaiz5w/+y2KZhn5AnkD4TwekZKoUXwDCuRG4DKHWFgFZEyeCrUXYmX\n6nx4SDpZtP1B3oSfXMfQR3I76k30BiCqhWyxaTnoTGhB6Amjazn2oYfM4IkQuhtcyFmImZufh8LH\nntlZKLNC4Ak5D7pPcIk6evQo1jecX7laE9AiyHzQuSdpkA889ik2l1LJSUKG54HSQm6QjpTKNXRw\nBSYX3EZeK7o6QZeVxbmVkVwGp0R+eRWrbXQIdExx66T8+b/6+q7tO48fOfnSC8fEjqtJ8ZGh0fOn\nL0ykYRCfu33fLvShEDLmFxfH0UDaPozuqAGahSoAidSUxZLdqYtuxTWjkDIkZ3abu2lSJi178ymF\nSxdjGKIA8gExefpkxIyuhDgctqUeTaUNogY9fw0PzvyvN2WIccyF2A3F59AXT/wltNy7sddh4Tsr\nDItgm3ada8tcPcIvXmjY7XQ06XZsrFQ3qrSdtuq0dmbTr37tqyM6YpihJNWG3fm+j/xgfXEFcPyK\nVURWAkyYHk/Ct225XB2Y3tpWov/w5AkH2hOSu2PH5I989L0xva6IxXp9BVFEoKXM5Ey9bhS5dgM9\ngBUPRwDcgUx6EPUi0qt6reWS4K5ks0DksLqeli2ZMsWWFmuzew81G7A/irF+tEMYZFvdqDsbFqkN\n5hPeJEd0xV66MbUT0IYfmxinAkAU0aNECAT7CY06JEJY3yCUARCF2I02DlY/MAtQb8Wf8oc/8Wts\niCJhxqmQ9h9NLhE9AYwdGlLX1mo6QcYbWHPAiyPd3bUlUy07QwPiQCrerNmvH35z/trym0fn3vPu\nd7dq5uriajqRfuDQ/pe++8bsrtnpiRkwepKZLHzKp7dn4ll9ZsdUxbDz1RZI8JBgo09IugE74lB9\nhCJRJZ0Ux2X6dUw8AjJbcHLny52qJz6WVVj+ITFOUChXcSVfB4/FV+a6x5dNIE/k5S19lnsoCxfD\n7cLNCZFiWG+/O/lxu5OlLlSq13Lny51gGS7PFfkDB0Bof7e4PLTzdwG5zpgasdomWqhAKQDElVbc\nMUlsXr5QuHQOxy1WKa7Y0qVLhaUVBIiGWyE1d2Qd0XSt1Vkqlse27VDSyTY0cUXzPd/3rrvv3jc0\nINWrV2ShEo+R/hJ7ExIT82BLn4HtMclB/Yd6EWguiMPhE6lNuVwViB6DHyZraJZiElAEwV7Tkmtr\nKCu3xWKD9SaQGbDOI+Y1J9eF13TQl+RHdHjFh/0aJCH8PXKJAooYix4rHsNQ4OKR3qCFyGtfPrq6\nxj6ASAN50uu7/9i/+w08C4zKOAQX7CnI3KBVB5EZ6HAMDsTQOdixBa6mutkSqqXalz7/9enJ6f/9\nF1+Kx4bA6/nQB+8qlxzo2MMKr7hWgG+HHom3OxJMCF2CzylORmxLIg7ItUYHzLAKeoNxNZ7WDJOk\nKXAtVdbUAwACLqtxgpe43pvHHmRKggoDmriBcqjXFKCGD3XKhG6oZ7+GUfcss/9y70vN3kyBVvRl\nlfw8qweytq7EIvgcmx4OVpCbMnkBcR3h2I0AC39Byol07qGjRGoEKLQiij2gi/FWuXH5rDl/qZ2f\nVx0DrSbA0S6cngfSFuvCUqAeg2YShiqoRO1KszW0ZSw5kh7bNibH5DsO7RseTTYq87pU16SmIoKB\np6xnUIFACTr9RgcQaHyifw1pNEB5AWcHl9eRTYJBOQphgmi0gAyUSOQowi0Tjovizt23r6wUwdjt\nMPslwRH7qooHF7AnmaEGQvct4csAv1IqUwnL/VmBwYbctMR86DkGAXsA/4rEHSkNUnn8PAklfPgX\nPs2qbZFIbRG50wa8RMeEIgIwSbkBlvrZt868/tLpds196hvPDmVy09M71vJwS1OAw0yns1eulKen\nJw3ThbMkYBAj43o0rRcrYPUqjY7bBOsHRB6cYOjHRknxBJECbljlao3YyXjt6MUiGBtWVCZmchT3\nEYmKN9Gku8QRxbwylbxjPcgl2EWT1+eVvL3PRkIOb7JIXRopgpfg3CiZCc8NroPSDDzqwlulZ7n7\nq1sI2xCEgz1XCvEUwkSZqZqGVzznYrpBduQIBIWHVTtQFzG7LhbnC2+9euk7T7bnzo3FZbFZSqMM\nq1dHhpLQNSiWK65kEOlcwbcTyEkbmAfFnMQIiiUjN51udYqtViGimpmYoAqdRrko6nE3NCDwxU2Y\nzCprs3aYCI7FNAYwKzRxe7EDAQW0ZbruUOFjEwpoZapqcmWlfvDgfZVqR4smW1RQUpXZi4fdsL27\npB/4k/s/HSQzqEGh8oWrCokodHgaDDq/HTrru3dzwz3Ur/gTiQ3Ub4Cl4RAd+ZHHfsUwjenJKOA7\nsSilVq2G+/zTL5x66xSgyYIp7tk63am7s9tmrpxbuO/O2y9cXoQ58LZt0xApmZhMa3oK+CE0EkgI\nNKJVm24RMVyTVsvloYlYE2yKNlHj0DCCTmQhv5JMxVFj5wYzKPmBIMBbj0UhSewkdHRnMRQC19dH\nc3Yp6bkkwMXRIx4Yk396yUpfyxqhv+zaDZIZnrtvnIxeZ7mHgVxSKAcK3TZPcSRIZ9ap5cwxL8h8\nkLIFgy7ewAm50bDExgH8EWdgKyIYGadROfPGle8+2bh0fHtKrs9fSEqWZDRGBweXFotA2gNIpQO/\nLELwJoN5CzqJLbNaai0nR+SlyuXMWLTtAJpUUgWzWS6AZJHQIoavIiYyYRGBiTSz9IAwfJjrs6kn\nXoLKp3AdF7g0FK80S2IoGmLhipxcJcUQakfHd0ZjgziUAGuFsZ7kh/e+NdXGzgy9Bjekn+UzQWkW\n1GpSay4SIXuYVou5cDqI7kALo48H5wEyrxTIuAFVbIvbX3703/0mrI1dMfb8c9+tlQ2Yj40PS8W8\nmU1md87suHzhSkLLJKNJuwW9CGkkm43nBpi2JjadAsYDitcGnH5jIkideJdKRALGAj6vyYHYyloN\n7ZuERcjLGNm/wnU+EYuQFhBjPJBCCrmVQ8fCMoFWaKO1S2Gc6JdUoZGYkOcdSda1nAnlk9hYOkOg\nRV4vrqvF98Kw+omoXrcz02OHvdlyD3xVpa4cVHQ9P9eeuLVOiQxS04BExt0cuJs22y9e7i5JYo8R\nMZvL6BhTdBqVmNsc1d3yuTfzb70yptpKfS0umQJBeKVCpb51cqRhdOBwC+p5VCPkqNEgqHHLquQb\nVm6rlBqPzBWudhwamQ7C15fsqKmvbCqiL5HHn5cGqS6rP1nyjUaYwtyHgD0kPm7bbjOCBbgjCgvD\nWAUEvsX8BuoKzRZ+Pjs2sQPqi7YrI6PCBQrbnwSLO+jM9JJ1JK8ZIIvreFKJUVdN5lArcnFzJl2G\nF4ptgPWNiI6GCII6foxECGHUMTOD74hfPucePnx+y9QUhrSJWHzXrqFTp4gSCw8mZunJswoKunyX\n1QzR4xAFypgOUydkZTklVexbgb0tMsiAURmGGAQ2v5yytB4I/WmiL9EfNrGRNpphWD1eP26XqKDk\n9jKwgofqTtalLtlKVwrr42+0WAq388XuI1h15IBPFPTX0MMO9d27Dm5Klf1IHxia+uTxLkUnfrUj\ncrrcroqKFRGNMbVTfe3F1/7qMzuscs4uxbVmpUWqMQ6M4hSMDBMqUpPBVV2KjKTGNEdbWS5UMYSL\nuwWlNvvIgc6gU3RKDdFAVgr1DTqHweSOdsSQ+fz6W5Z6mEE+u8rKClLDFetY5fDKFZwo3q4LGFnE\nqdXg9zzYaU/8zGO/cf5CUY8mceDQ3KdDxtFYb6BdY2mCAlZhTA6W9fWSlUXL6csK4t1npCt4KFw9\nrtiBixaJJ/hENsAVI+3hQmvkkjS3APhrBI+ZTGfxQMWSAH9JPQ6oSRTrm2A1HaYIz0DfNFu3u/Ts\nOByHvkFpudfqlliPmanvBxBCsVtxTrwZ467r2868jT5hPTUig2N9jw/ugci8ZqbgfR0SQxHErpbP\nZk9EahxuVyuaf5Q68IQxU3rEqFWFdGTvPfd//g9/P53LYB5zvlieQfpu2xHM5prAuMvQaDGbGNAC\nomBwhg2qV0qvbWHl2hIoMfpABOur0zZJKxWuRgJxrIKOCAMJBZMguXvr80lcwDt2fXM+NqRD7t4i\nfShbSBRa3MADGlXt1bUV+Mp3mAAyMg1eU+JrTuT19C77oUH7CqNzA3h+UCB74SgMLHREdHyNi4Z8\nhkPQsCs4JAlzmsjEliktFsnmUlosvlqpY3SL6YRFYoG4LKLJmn0IUjROhpW76H1qJOZANRMQKfgE\noQftQgzC8SdrkIMaKaiy0K3D7/ZV+r3+Ou459TYWOm/Lhw8xX/ftuLENUJ9DY2M7xb3hzuy2qbrB\nh5qM0OgBXDoxWiq0rlTM3/+7J141hTek6PDt77jYsKttQF+EODhX7Xq5ON9qOICA1yoQl29hJoDK\nQLJF3ZFXr6zUFsuqoaaUlGC4wIEx3qvT+2GHxwViT/8kTBkPjmQ+DIQ+PfF0OzanYhBLNZnE6OfJ\nJ5/ENkCCgdEPWuMI8JAKC0yaNn6EWTVh/2cqmFk5xC2CuRsCvkkWqpAvlaQmkyJEpMcXfGPQ77//\nX3yaRIfhdaqRQB9m99G41ACY0G+MMSUrhbzI2NaFJSGyG0x5yN2ddQll/08PHIypL8v2WHfZFrnM\njdvDctpUcdfdRAG4R12jZxl1i552OTdtriXYy1AJydeIYZWEzaeqfbwQpA3+ZL6kq9v3mR2hp4vq\n/ZX40Y4dTrF4CpvH2MayR1KZ2loZ4lzRocEzq0sf+KmfPLUw/8yLL04MTuqmMxqPgWWkEB0Mq4GV\nO+CKQyrB4V0umjljDaKxAupRIpnCqANzPTAQqBfmOj0VPs+//Lcg+jo//vK2VZeSdYOFdqTvKsls\noE2jYfYkwsyhVBJmtt5+7Pg5QGsz2Qxkw0BKwowTdHj8ChY9DBuxDbArNtvvrieK5/JqjSt8c1IC\nV9LkTkcCK1UVNh/AW6R6j5V/tFdEicPx5A/87H8BCYpqIBLWguOwbNgCEncUJdQYY/Jw+EQOz2Gu\nGjnmMPK36HqtA/+4ZiO43oKDZs7+sgvH6c0kSAVR3Gy5XycF+qcv93Cj0Ic0s3vsXO+XN+buDBNL\nFTdrrAge4plU091wYrOe4Yg9/phuj25Mr58Z+Ae22yiVx0fHoBp/bnE+PT1Z6JgPPvzeQ4fe8dIL\nL5utTq1dg6VjxWItE6aXBXiLYVr8xdCAkzEHQSjDDYa2OgYcADu6eFxS3HRCYrRSsLL9he74XCEv\ncxEcDV1BgJvY3VddTKkcmXuN4B2Y0CtQc3tnH1zNYyAFqrFy4MBBNMgB6kLMRj6DsgHRGTrAvIvi\ne4esRwrHdnoOyaCu4wE5qJT4X2ORGOZKeHDEeKbPAYZ+kjs2U737kU+SaB5kn/CwII9gx+DpEdAT\nCY1hAAWO85YJd4oCiJoIYtd5zTslgj8jFDwqNlP5Ftl5EV6Q1x/rCP6+6bGhDDdMejCx7tu33EPG\n5KE4416nEen2fM2fMaz04n+9eSYjON19JO+O0gkuiUEHI8iNSDdOBYBZuzJ/NTM8iLFWNJGam180\nOnYsmv6Jn/54qdlaWltD9zcxmCwbDc2lWAVELAZIgsSOXRK/BjETAnegOKG2Qx9Nc2jc2YFMnkwD\na46PcENTCLFr0YfZ/gjnAI0IHbYWEAZ1QNkJQAaRBchAdNRsZuuBgw8NDI5nBwY1XcNwCmUlF39F\nSsNIqwqvLPtGd4lfBZmrUXEpKhpA4pt48agJ+Ogdn3hroE1ZrU5uKIe0BohXUJ/QMcU8DP1GZDw0\nMTbbLS5MC4KFJGsxkAmTEU5XoXVreTMeKkDRiYLItdsFABZ8chM3PBT4cvf+ia0cy+3xVv/ecutw\nT6Mror9N6TvHoIZzm5tM3HuFd0JV6frXYqhU7dmVbs8MWOyRJez5KM0vRxNRUROmZ7eurC7D32b1\nytz9++6eu3rZkMXPP/1yYuuuyYRszJ1evnjS0a2oUUGfHPKEoNyDagBSl9txogJ6RWrE0VtVq7pS\niebiWkw2fHxdd9oZdnt2N6oMiTTidrgFPGd6UaEPBCGK6Q40dmxmJFgHjxQL3HIhbZJEAoWrjeyl\nxT6oO8VCb7Dcw4e/FCpew4UfZ7uGRcKQteObaPLw3B1f8HQf30fNimMEXyjZbBSvFkADlQkTWDTD\nF4vlMv0ORXTyhaRkj4GbcQIIcnAtJCGsLCz4a5qa4p7aB40kHCc8Entbi0tRePs+uESrp2Njh4O3\neEt78m15TRxe29uI5OYwk1vWGiUlpbcQilTR6oDd6P7DX3/BsMy1Wl6MQMOjNRoVh0cmJ+KxSLNe\nOvxtrCbEYKDHwEQXyM1agNwHEOxRNWK7Rqtq2G1TB9xOJov48HL3tYbWnQYFwdlQO7mCGHYm5PUr\n1R5gZspydHJyGqu5WoeahpEgq692OCFhOQw1y4NjcP3cZo9p+Xo7vn2JBzfC6yF9YHYm8LOC8C8Q\nbxJUyNdA/g3/9K1vfQtDVkydvv3tb6NUQM2q1BqG9wSO6PmGusJgMu21wx2vGcbPFZSdcqgn7Toh\nCLjXmaItHhays11vii6IXZJ3zFLGm8Fz0f6geOtrM7tZfJV4B90Nd0LWX6FNeYkUTiYkr9/frR7r\nepgc/hfWQRU51VEQ1zUAA88C27GDxqXoa897ZzshxCmP7NiGyJWSREY3dei6MDS8E2bxNW3XT+/s\nAD7Jk2IGFSKEbSALjB9ollW7pSxfvbi8fKlYnrPMBhR3gcuFKfZwWoUkjmvGaqaCmWoklsxND9wR\nH37tpedSqtEoX5twnYwqOG0Bc/SObBRaggkb9EgKosA22jYmSk7YvSqcpUrvVyaaJW9AUFFIS03w\nvWV4x8Ym/UAxIVqa22mRU4gASRkF+sCY50bi08uLzeHprTWjDmEXaOEIJqjI5VBKiNfbCsZJfU9L\nkpBRFGhH4s+777778JE3Hn300VdeeQU/BvUrXBMo7L3vfe8DBhg6HyQ2aEG7ZiQDjStVfffD70JQ\nxw24/c47MGaiavizr5ub27ZIG/ToqM/ee6C7YjfOROziqq6jArvl5V2pGyYhhuc6PaMlvy7p4znI\n4TTdjb+eH+uSe5E87cWeMarUlZy4Ut/aKJj/CSHEougKYUX5DqMpUueLG1Hwnp1DR63CDeV4s4/5\nEFKU0mV/I9FDUdRhCANknyCkAZOF9m+r0cRxjG5GAUox+SqcSWENSZkl4KQijfbQKgPDU1djTA8Z\nKaxMAoytEmyD73GuTgymT770nA7NhkIFA0apI0A8pt7ulPECktLAjuHBnVl9WLZ0LPuOI4Rx+aLs\nA9qoFrSoI82bg+v+3VIcbw7osIhM/r3EbSWma9SSEsW6NDqx/x3v+sFWKyrYCaTWVMvKtVs6q9FO\n4T1EHHfI9YER4GhHIAJwAXmXE8kSlj6i+1tvvQW2Pj7g+0c9p2QS6DHwYNifQPgOKV2WYH102W+2\nO379PvT1Hy1chnb17N6miVKPcXYfgHvPF/08AG/y4mhkkwvFMasFKm64TwqBK5cUvjmaj+RgGGPQ\nIuUWlwvbkWwpBPkUGlw0G3ajWlhYXV5bXaZTmPjF6iAmRyMGH2OwBhCOEcVGOWXLyQgR4dBSAysU\n2BhRgJ9rJwUB+6xqxYVf/9zv/dZ/+PfIY8G8mR5PnlmsxVVCnmuJqBKH8A5wwzRfsbFkLYUbxfiC\nn961CkT7iMNhC56Ord8hIYC84knyMUvviAtxyo4DahFGrWADM+Qb12W/xdSUucDil7HbX3/9dWAb\n0XjBrOrZZ59Fzx62H1jEyF7wGgCMAaMvGYsfBykU6IZ2G5kSMpkLFy7h0uGH8Vci7222Mq4T3btW\ns3M95dSNztT+ZZN7fisgtoUbT4HOR7+wfbPRvesvnslJz7voDufOpq19P6K763Yx7nohxfKcECdN\nWsfJBCCCQJiA6WZZ2TitYzCakZ3CTr5UWCsX12BnV6+WNVIydzlkFq/PohlKKz0EFjnOCoASUW1o\nhPx3NYJyESEYx0XT7BSNThERcO++7fffe+f01oYAIkix2lpY/LPf/h9mvpzTU60a4IkdLR1JT6Qz\nWzJ6TrFjgBC0YcWguVEflMvzmHX3Kg7l988iP5BpSVLCt9uSa0iUAkG6B1PdJFSwXHXkwz/wM7CU\nxiJH7YqpI/oWGHHdWk0lSojTCM9IVBDaEdSxjnnkRjGKr5GucBI3vuZqmzyzR+6On8ehmsuNkO8H\nc/9Qem7n5u7V1wnh4s2H9htiPvt+/3uoSsPV/U0cRN3nzyb4yhuWEzxz4hgKz2yBZtptonjqCl/l\ntEg1RFX0EpPENFi7WqqsFQt5KLO2Wg0c3oj6EGwBm5yaHkTTxYAbjQS01EAMVUtrayKN+HQN7AAp\nSvsXDXUBOqYNQazXqnMoVd/7nv0PPXSXgvbMtRMX5uoGDKXWKhlXfc9HH339qe9W8kXD7mQnslpS\n04fiQlI0iatsMjMgoBk9fBg/aYNOhCyIvpuLxIcN/B9QBehEWVAsA/hXWyM4ANjQkhob2LHrbsvU\niawM90YTTUoTo0zzFg9qiIRx7XIsccRvfIG6lpt0I0xg0WNBY8VDLhg/hhCO7+OvIC7hEEDgxxvD\nsYBf4cBJL3ff6EIaRNye6C44G/aD62Gh+kbTkJPeprl7+EwIul39YGG3EN1Dy10KvwXZa/P1pHBS\njy5a8Oa4klu4EcZCzvo4vSd3B/nK9abubCoN+SM2dRZJoZN5QAmka57Pr6wsLZfKRceo8BG3RsY5\nJErCerpoEVgq/bBI6TLD+psEBgHHGWoZMnVaiD+BSI9ZU920ClYnr2vV2V1D73notpktqcLK5Xo1\nPzSYfvHEeQvka2AZTbdwbXEyl1u6Nq9rUqVeQbSFsKmrkIAQXh56k0ivfOSTEMrd6d3Lnum2F+mD\n5L7WtBMxbF2UyJAvMyUZbg5Jw86MT9+977b3NjtRpiSid6APJ1twmDLcm82NPdAEOT7QtUWaHmj/\nY+nzXwn6NljQHIoDyWwsRax7rHK+Exr1FnAKPLdResJ5gCe8iWz7FhJrH97o9jTsrg874QHmn97U\n2+yl9v1reEqw8bi4YR3CDcyYep6iMKgFFOCQea/ll8rFwir0GEpYmgYWN5DPkBPAOmRPishokcy5\n5Ekqm6wDbjFhVq4m6xJ0Wmujy2FTRmaxmOzaHVmCWkQ7OSA//O4H9+5GrrPaLK0lST+vcPTF1xtV\nGV6hK4XSe9/z8LHq2rGzrw/lMkuNYmw4hq6kRaxgEO8kwlAiO8JjRlrdoBVJ9AwUHMrK2UIXHCHQ\nAtFkjallQEsDECoJjxiJxQeg/L51ryTHofFDg3WouikmTC0tEq+M3tLtg5ovEhWsZq7ziK3DLYCw\nsn2dXdKiQqrD8xksdCQ5UCXAFyheEapA34bk2De+8Q30IpWeNmrwBTcMurkFJN5M1nGT5WafQcY/\necnfJE6ru3ncW7hvNITwDO783J0X/VCfBZYR4DzUc8jA55bmlpfmq8U85m3o3UG1G4pOcM4GdhzJ\nONrFIPd7/oESPy7s9S4lB3DYnMyKkQ2F91ZnRZEjpGYMEzyqDsleFTyZj/7go8lYwzbLCgQmKoXF\nqxcr+VUcD+BrgLHtqtprL784MjpobxsvVFfVrFy1ymBVS8wCTYN6I3RiSZ4M61PkpSp5WmIV09CI\nUc4Fx7PKENww7yQeT9UbJTLIjpDqFhIreOVNTU2PjU+trlkQ1cX+R52GJ4ElRLtV0SOpW83dkbEA\nLczjNxd/xILmMkwc7YgfAA6HEASxGEz8uDQV9FM5c+/c2a8ApPDiiy9ih4h/fMTuRil0FW1CH7x4\nf0eDQF2sB2QSjuIBsLanybixVnbd3iXoG1ZuQAh7Ja/Qt/DlTxoWaoWNt8wwQ1zaxXE8gV+GI+DS\ndlIwqKOiJ6o7HATDfWYcRpUFs4FUeWhIITN4EneLxu+VluZBBy6VChAErdfK+KdkHBEO0u+yxMDS\nnL0W6EVaOimIuAz4hP2g0dDcZfbWAs/16Q5bBk0zGC4QUqGgqrfgqtAyRkey+dXzdx4cfejdW6ER\noYp5yS12gINcKhSW0Owmi8kqGjUW9YgQEcmDyDF5iYxL4DDMlc+CFXgU5/1TPz2z2AaWOCKFsjLF\nIyeyiQTd6SiZFEJ4ACjyAVdMdoy4aaVdYfiBBz68uka2eZF4RNSsWjNvCQ10SGtrcToHJErD0Cel\nlisUpk0UsySzDcYz6fcjGcoOQv4OT2q4DbdTl+1SSm3mUkoaDk2y1rZib7w1v1p2ZH0ALPByMY9p\nabuxBm2eDkgkqFapB4bIEm8ZnWtXgUhbRUpDhE6+3EPJrtQt29lnuferKcPLqz94sKef7c1lN5S8\nIbeP6wXm8HLvMuILbaRwmyXYU5LAxUkdljFT/KTEwIIXTTkKGHREY5JMArPdxN0VGh2bO8ys26yR\nXiQAKlHSZMOitCFRW1tZXMIqXyusZmJRStNV0l/BXURrhYQjbUg8q5weIPv2WV6XRmG9PFrXGHia\nMrO0oZF4m8SAaLqkyJwhSqwF10lGs/VaCWKu994xe+H86wf3j+7dPajIy6KzahmruOWtWrlRhrwW\n6l40K2WaorIEl3WvRUZ96HDKc7DQgy9YNA2batnBcmc6OVzW3D99JHagWYLMdSI0OQqnjlQO4dgw\nYhcvleDBDCKHAzAy9SWJ9YLoggKjRUpGEFuN4Klw5bHQsUC59eTwyFAEEzNZLFfW4CbMAciDaXUs\nJ02NKmODYixqQyipVLfi6ZnL84asjTbbkYHMOFI7s0U0DlE3jbZZLlcgFwXPHNgaHz167NrVRV2P\nOmEH7hsurHDTwnW7zvfr5Ak3zPJD24avpT6dmZBh5cbHvM7rFHsenNc+xDCDbJ/NQnaHxvV2xx4d\nyYCHCUIxaQJRDMOdsCFimwF4jhliimy6STm3QuPOSxeuQVx8ZWW5Wq5QTqmQPn82lYAiejwOt2lk\n3Z1YhGT1Ie9rOlz+yhFCFpB8lbUgasLEmEgnkYEZmDaOlM4M8R+2bAbcZQgptEAaTRmS1lankB3Y\nvmeXdOcBLa4v1CvXFBTA6PCsYcW3QSICD9LCAhM6ZIwj2px7ylBQNg42SXQDnSb/hQTXyurLq+D9\nK9aQ8BQTPIkAKBEiWgNH69Txf6huwamt2qjuvW17vRa5Nte+dL7SbACDPhnRBuApOL1dYUA3UpzG\nbsZa50M5hANEdxw+ELAeGsyusmmDSiYIy6rUEpwV17rSbBUlxYIuZjThtMxrOFXbnfFTJwGE3lIp\n0DkKm+FK87LFJArTqUHIWiMS4XCEcotFwGdR2ZgcX7985B7qvgdTH3LnTabsPd5Pm1E1AgPoTbuc\nm3QzN/sViE/gWujUFhTIcsshsJGaEAA3QivaZoURxJZpczmwJEWuQScCoAE4e0uF/CoUl5eWyqUC\n0kSGG3cTZK5ISndoyQGFB9Y5fpPRZ+Sx0SFIvhSLa6CFsbTBEULECX4MdgyeXHHELVeOon6MQf6Y\nvMMtkzSXY7LkylIs1WzXkllIJ12+ba/qmG+2OiW7UaBIWW+YGJa2aQpE6GEVSQZgMljIvmgJ1Z2E\nVhBD53YXuJ+BMkJdaSlMme25qvxrNE4UqjowJCZUTKuOnwZ90Dp37vzAwMy2mamt0wOqOKYoQ826\nVCjU33hrDn0VBBgoNiLQJDNJnB5Y2SyTqZCQraRcuHBhdGR865ZtGKNOjT4DDyLoKULkTNQ6ZL8d\nVSK2uLi6NDo8XoCdQeHcE1/7smFlNHWkWGzBpwxEKoR2bKFoJM4yWTkeT5K0OrTwe6qxDU108Z84\n1OwL9A0/V8/PcPH50FOvNzRvyB66me3Hlha3B0TuYLKJIERbFcwhQDvWIhrJSbQJHp1OSuOjiTde\nPoVWQLlYwgqGODXpGOO65obIPYr6YKR3BqFnKiwViGFozUaFZcDC+OjQ1OREo1Erl/J4uxh09HC6\neOIHgSLBY7XS92zGvuVsS4d8y7BJeJeQRq2Ax6gOCs3mobsnts+oqdhavXwpl5GMcqFatUDMB/1M\nYYq3FlOVQqqPvij3WyG2B1dM9+yKXE/HG8ecHQrkrhSCQHZVVv7ETA7mUPQXrUY+4Az42qpbS4tl\nQFcg9DE5NuDAgaV1EuNhaNdFtKymJlJZZfb2fQje0Hicm48vLJSqZWNhqby0mMcPXb128drVC5NT\ncFqFXntt32z6V3/t/9GlM/BUVQD1gaRoxyqu0YuGCFLbkME2Rcn/wF37vvqVk2PjsVR6aHhCbNbq\nyemkqABVAYyaUa3gNaCEMBkI6taTmR6fx41x+lYBvT2Pb1n299Zb3BDghb48QTQHyeYT0GdRQrIh\nEwaG2nkQ4EZXEA3ydlNcBent2hwk9NHJymWznAafTMRQ+rNpKGJYgy995n3AIO6uy6HOImn5ypl0\nJp1INOvV5aW5SrFAwtm2GayhYMXQmMY2OX+cucp62Q6Jy8aiVCl6MjMmwj2eGVUhFH3f++h9sFHL\nxhuddgFytIXVElpBpUrRNnSXbMBJQBjlAp1foFbqnusTb7U5TLsUMFdeiFM14PAZguABW20p7L3D\n52Vh08Ywi4t+UQWQ3KHJl4yGt1sr06mYzqjwHwdUDNqpmQwXGilJTEs56uY7DoyFB9DJcZ3GlctL\nFy4gQrdhlpFIqvcd2lutX9o2o/3cz9377ncf6FhHo82ag6SyIzM36IhuQdEZIzs5AYPVlm3C4mVi\nVzImrK0sLixXAOAR7IhJDCaNpqgkfO2gJwSnN44WvuVkZuO4saenfp2lKd4Efr0v2rvXHucmMOhh\nBbzw40MyGd9VSXWN7J6xnkBqwzo6f/pysVDA7AdLGb05nK1Q6E7ksswW0qH+tOlBPSmwwWcoHqHO\nDqaRtuU/KcXnhI5MSYelVMdsLi0XcGRjVWiisoGy5AXRRstAPiqKHhmHKm+iAsHesQY+WQR8Olj5\nQQumsIxEqlIufuRd9dtnsf7mm2W0NZowdpxfWUpGYy1D5tgVcglG0xNFoQdh9cFeMt9j3BWHGvmC\noATTMY6tZUaWWiBIzxuORHDy/xrKaSVG4MEDKawFD9kZlVknOh1DajWJLBRPEnWDWTxgqOAg2cPu\nGkrNG3DlchOpkbGtE7n3PXwgGh1JJoZaTbiU17GbO+3i2Fgsv3KhUjntQLlOwi7CoYXLigGWAkKK\n1anikqTjcdTk8HmR1cTObZEXX213xE40OVirNZlsv44biKwUHC6S32h3uFmxcp3e9mb5Rl/41M0E\n+PATbTZCCvf7w68qNLUVNsvd+44Cej6SCVrkeLBKpTq3QqNNzH1oRh2LYmEko5F0VPfg1TgOKZ/Q\nXd/qmjJi0euOM1GWDjeglZm/ksmkx6EcSvw4O4VYjO4KEiTI+9NB32qInBvmcjMmD7dN3mWkFMov\nNOsAsrUFfZZaZe3S6nxpbalVK9lmg/EmnO9//92SPYefYcmuSWaQg9NXLl1GkkVwXJISIKamQg1a\nyoDabqfvLSClAwbx5deWoUposSJ2el4jTGyDCxvhg/H8vffOQZGoWEiokSRO8bBUF1N5LJJAebXa\nSMtKFE5pHRcQCgnNQQjxqzEU41p7WSODupoNwCYdCXKpYi0uGzQ8wPlgwEtw8PLJZkxPKZAwsGEd\nZ4FcapDIpYkqxnJastCKaW6rU0WGk4oMlktzu3dte/P0qVh6R3pw68hwFscylHdRsKsAvFloAeuY\nrbY67HQNGpE9Lbyg796zE2y77yQy5AfvdEl3B43LnkYntXJtIRBGDKhucD1lrGSRN9otolqIfGDG\ncgfqpuFhTBq7UECC0wg9msC1ihELWdeIjQDhRIgUAuI56Qw1BiFaX6mU5i+C2raGnhfj0Up8g5Hw\ng7jeNvGLScpONApaTPrQYZJafMgiETSAcXEYzd6kJYVWAzgxYylIcNP6JgHFtul6yv8iE0+kx3FJ\nGpoexBZYt5s8fVXdjUKgxjVhDrBUrlyqNefLlRVyl1b0Foxf4jqkqFeXCv/lVx87dE+NmXXhWCZQ\ncZV9tCEvzYpavG90mZhhvcjtjyDB4tWgIYNQXgS7vrCHx3XgCsY0srUDaQA23jK5uUiPWKkHfXOM\nYKJCl5Saldj/bjIFb2A1CXn3COpjpM4WeZjhYphugD8LrzR4ThKntoM+o0HHDHXfSVYAFadD0CGy\nyWI9ZfayBdIXGBwYKeabmjxUXnV2b79PcjKZ9MgLFypPP/vcmydOubDHEVWU7mh1KlDc9tT3b2XS\nfktD0+tHfW7wxXeXb7dNbwabkvWl6Oy1SB2YG+KJsUSUNcgxk/CiC8ypsVDLNQfNPpW1z7G8WkC9\n0UBGTP7/zb0HnGR3ce97+nTunu7JaXNQzpZAIAQCA0IEkQxIIopg4jPPYF8/X2dsX6dLuphkv4sB\n24ggEBksjACDQBGllbTanGZ3Zndi59zn3G9VnT7Tm0CyeZ/Pa5bVbE+HE+pf/6pf/epXmeTQRIav\nmD1cuOee7UdnZzlCPGImmlYdkrg1TFiVTpjTtbLZvUbkkZC3GBeL6VjuCExmes6sC5EdjLmiIZEf\ntnkQtoaXq0s6qDEquqDxIO5lK+eVktS2dYVjlQaSQNL15lAYnZ+vlZcKjWqh3VxstefbfoGKDKxG\nVxpN5Xvnjlaf/KSRLWeOt9qL0N1tBXIipmnRQxK9VQaRKa1LEmqdKv3tBOZ3+qLzvh4imxhjwY9d\nDVv6OIg+PN7vNWh7p6HyahbfkTQpBinOV6xIw7doT0PzuHEPgd17YYO87G/CEhWOnFZsonrd3CBD\ncmRzw22RCyAOGU0MrpQLQ7n8/plDd92zA4l3BFuT6QErzLENobhtHxs7nXH7J+ekvxD0OAHM6bu+\np7Z38SDdE3s7RPIvk8ApV0v1nsaI6B/w+0KhbGUX8hTx7u02jfQy6iSdbdaIFbvpZHIQDkqU1Mlp\n1lq3/fuP2BDYobF+Ls3I8DhGq35KeuatS0MXT0vvBA3+A9pvVjPrMdPHpRVXlnttU6vlMJCSibFJ\nWyf1SjOY2SlD6uCeYPotRuN1A2p7TPX9vVq5wdYN68vR+VDgweXiCmtmqcysB6+Foh3wjscMlZYb\nr8Wj7BustDipAU7KVSmtq666aGQ0Wi02e6F2mxdxjv2DAGT36A2bl4nIsgL91Smtq2bt+36fMIQb\n6WsabIZK80w7DTtUwmkMfm+8RKDU4DvHUwxXg8+ubhS4oWhkNXCN9OoP/ZFVj4rm6lwQt6PzqqVa\nF0tQUfZ6OF5wjmLxgibDqEDHt9bmWtNUHinVqvc++MjDj84sLK9Ikh6J6qBc2V7Z5E3gJPb4IbzH\nKQD2OB/hAJYTyDbAo0SwaakVS+wolZJm20R5bHBXuxHEPwN46qiTTfMzebdz9Ojyow/um5s7ys7O\np01NTno6WF5npKLI5Up0Wm/BvPVVAgfolz3R0yFYWCTT58xe0bO3Pt8iuoasFu3cCRA4Nx7OS2FX\ncKVxV5r6NbyVRcICanYsBvfhTgmng/yQBA3dzFi0UVlZmF/g/0CT5WIBt8QRpbKzLB5mGyVdIc+6\nYP1O3ZcE2ZH6J7Ng4wwG9CbGnLPOWlcoHPEZjS0XL2pyWcaDkJHtZgh4VBN0jgTeSsOG3minVR90\n3HCYoB9Ng6tgSI4uIfMIPXOP9m/aYVTjafbShwccZzB6l92QJa+9XH5P1cfvb4rlI5MJBsozOYvh\n10RwDWmq9YOYVjio1qEZCSSMKowCH8iWiw0wTbb7dH7osUdn7nngoWKVeVXMkMTvwTr27TAhLKQz\nmV8UzJwQivxqFeoC9xNxTyaRc542U5NuccrBNsQLz01cDhwlGiEDaTQuucfHjrUOHzt2cO8+wjhu\nvLCfswNT4xPiwEluUOMkW8oOSCyhJXg8lRQ4mpWutl4riBjXOIQJPlLkx7ipdOAz7EvZSYRoGllt\nUHSCMpG6mY5qKUrvBfGGb0NEuBm5+LCkqgxqQLml2SpVV4orR+u1wtzMfiCFTgtRJNIyuFOxkUHS\n1GirDcIDLC8fqFsNt0jbV1mDHYhmLm1GzFO58vINA9lEuTiTTgYmqHCqQil6Kbs9HNPpUzIUpfHY\n6iCdEEBTU1Zao1Aw/H42FNG4TkwJCq4hc0IE7nqS4X1dTpETmiXsgvTrjoQFE1OnifaxVPrSRalt\npyE3Z3N+mnUVa9KSJaPzJCqM9AY4SxLUjfSov91kmkSZ0DcxPLZ2caX24CN7D86tdGLTevRx669H\nK4odgBYv04o+bTDTz6v6xVDjf7r8FDnVl6ZTsoPXqm22/lyWMESapolPWJdDY0lQh/37l374vUcW\njs1ji5A8iQEGM7lYfhhbqTOhhxk7SQGhutrAUq9WTUwQg4CsB1cjm5HYlOVh9fBwMp6VrHlvJjNs\noY4osOEV0kJYDdSiAmRCTFG6gAEw+V+7QUjJGA0VhmEnLkINK5aWahW2hyXQlUplka0iHukShcN/\niSY92bQ6jWpNQnloCZKtSqnLtabQiAzhpjGUe5ZGZb/bRGvXOevMzcxSjUUa4sGF8xNbDXM1/+kl\nl46tukiQVvo60C/YnXr7qh8OCDGkqP8uyJI7VZLWq/yuNmT1j7syenzYI9/v3aWjxdNs3eplkVNG\nDSSpDDIGG3IkhJSgNS0lAvZkhxn3AUVPaP8yoFw0ERjaWirX3FiG2RmZgYkf/PDRx3bPNr00XGZP\nKinBgepMNaoMrkR2REenC2aOoxE+DovvQxgf126gKlmRfu0hcz+pmORxDnU5WM5JyVaXFyrzxxYO\nHjhAcdgTSDWRy+a3bjiDzB1bYkW0agxhkFL8ANmJzijFynHKYHlJHWXYbNU7OjI8nUng+LsKMlqS\nGphC1BkZypsrAg7QEdhR+o34q0SHkUoaaJ+IDvcT9dBYqbgMyZFQMx3TgbjdMoJBzXqtePjBKpNe\nCYTaNSi+6A0Rz+QTrtQFkfoBAe4IWsfZUfvIpN1ivS1jHiBYyVRxyAaURxwRf4snbIsnxqCbfnSU\nWXbH2p1FpMnV1Dom6Ih598Qi/IDIFSga2FTRQMGlNwgteoLAav9kHruDCBeFKal3fA345EpI0Kje\n/2RPYSgajbruiRVM+fJTiB/6lk1xQxkKkhKkLSItu1FfR8o52nESjlfQXELoRbDncd7Qj2O79h65\n/8E988uNeGxYsFWJ5qLBZBRVTuczUvCPT4jdT0VWWc1Fehb/i8z9dK19pyzmu0EwEwn54lwgeoV5\nX6FQ2fXYvgP791N9yKaZcJwDkktk2Mg5d8HaoHbxHqYUEY7D32XusbYCSG8PftmQNYIfR0nbhl3S\nAEq4zOsFn8mIOuLqvVRKopmLgSmatsrCiBkMHyRoAox76oHh67Wa1eWFxcWl2UpludHA1steozoU\n3SNW6CKmybS0SFfph5I5NIQ6HhPBkZS0gHquCFVw8szzIfOGRyZmKkceTwoL19gJyGHEI6hhZenR\naTSWarUj+cHNnmdIlmspo9JvvDA+djxzvTrCTRJ9X4aC9Lx7oNetO14QbHSPu4M28bO3PFZ/1e12\nQmKwEj2C6Kjb7Z7y7tu00N64Jd/kz5W44/UkpPp7l/FiaVMWMAg1ItG64DCRYFx9JFAW7rUKo0uf\nSA5oUSx6330PLy2XQb+isZS0q9C9q6RuMr1QUZXzkti9ny9h+jj2aDTroeaqH46OEPg2Zuh7OO9T\nDRfxy7pOsocTjUuOaMlcThCUgsKRdDCKBiUeTnY0GbdE6a9ZZ7vKMR82F2k0IocPM1fhyMzeuigK\naZw9ObTVyxN41EkA2ZQFWU9JG5tukW3N0ogN0iAuzVZNEGOub0KmWmts3RHJCkbN1mpE7oTWWPjI\nyISmvxIItAJqu2uCOTJjSxkrOviHxdf20CtCadcbk5Q02pUJUnxebaVWBDVcWTx2qFlZbtULcRc4\nxU97bVJgWTXRhKPjHuiH1ruZ1svl9M9VVev0ekNshHFM8C5jLSQ5gLLN7EFpyWaHa7cY3O6MTKer\nMvIuF42cSTEo2HQjwQhOPWBK5a54PRHG4CIIhBgM94rUZSsQvLtrzH42BbJ/+kPIWMA4JZVXbLur\nkkAyla63NnrkAmstb5mv7ZuEbJigK1GC0SQFYolrtuArNqIic66jrSFdDWZooIqfJOks/wRE0xwE\nUK2XJUcEyZSCkiRL0FBTLnKBYlI1aAWMzayU2ClLE4MbYs4sQNfg2NpSmRtJ21RS1EzkdlDbJRPr\nyFxV5X3HQnmg4+QGeloiYZE5TKU7aouuDNeO2Xhh/BAk1fGxdK2KB63bsGMr2rHOhoej1WpbaPs+\nnptR2JJ08q7hvFMpx47OVh59+OHDMzOw73G6mPjw8LBhycpebHhWI4yJjKAgUJ0gYLU7x2FQmOHy\nJkSslVuCPVYRIaQezRvNi4+NjOvyMFzXqbeKq/2sUKrEifo6ABm6hUzENU1zsthITCGz7mKtXl0u\nFUrghuXlWkn+dmolrLrbqjpe02WKtSu6s1Fx6nKAj5PwvIrbSjDq9ffvBtRfLW1FFZ43NWdI48Q6\nx1EqxJZ0smNPXM49nnBBXh642EjfDEcwqFhch5Z2bZSDFBU8p9eT7Vti0B9knrLkovtJX0zvWZUh\nRG5P0BESP30CkbvH1VltJ5JMvacZZkVLGzlIea5rlDySd7+7vFTetPHMAweWqZg+4+lP+8kdu7kv\nbiSXyglLvtFt0/qbEoKxnB3YninVx0Lp1P7Jb/2tQ/2zNGwZyMqjUty7EKp05UPoIL3IDUjTA7Yq\nJHLVoKh20Qd0x0dz2SxkWKdUdA4enGce5Y4du7OMtR0YTMYyI4Obh3K+Xgq3Xi9YiUG2ZZaR/LGe\nGhWB0NKDLX6Ybpz60OggXMWlZcGweZ459+Azo8MjGszUASUbfttE70FzST4RftCbouBMRCrhCSk4\nJiolaZFGxoiEU0TBib5L0oiwvHAXq45wvMvkb6HHsAt0HFcwfLw0RRhXZqTIcC6rkxKdPM5e3tNw\nN9yeoVgrqpNMCc6IB6j7dSfBE52+QY1+r6EmjL/7ZxEHCHmvhhoJ7djWj9ABgp3b1xFoESt192GI\n/slRyslZmEnHKbmgJ8utwxKVYe+F8wltkN/xH9jXMmHDXCOdXjrn2B89fvk4XznQYCyQ6rjMuCd6\nlKhOkPJPT215+Utf8MMfb6OfpgPpg0COu4jDJdH35d5I5BONiUr2KSXSgxl/7ipiGpq7TKyWTNcP\nASa7uBBZiTXwv1alxMIG8nHIrQgVHjvm7N99ZN++A0tLK5xQlupyJn/uWRewFcCDa9ZKrBPycbwU\niCDbJmlls1fHlm1E5nPHiEkUl5KCBB6UWEaqSO320YXDVO9B5aGVcrzsDNg9C2AoP8gFZ1vTrCmq\nibnQOihXu9qEp0QsT2JmsHyvNTE6WKtWVpZmlxaPFpaWSuVCq1pzWg0nCkGl43QDynhEKZB8lFTL\n445OenWlmS8I7QQJOXWT4akSfRPl61NG8PqMXoFFX0JBy78jXbjgol1nt8PGx/byPnOTfn8zhhm3\n6HX0sL+ustlsczaFBc1qIloY8CxrDc0gdMMnDBw/4Yz6lZM1xceFwF5wdCRAqEij1A6VSfQiJ8nC\nBsx77wTliN4YDNcPcjwMQ0TpdXg6se7g/t1zY2ObpiamKzXvupe/uFrp3Pr9n7BchN6XyUKKlNJE\noy11+I4I/HqGZ4UUiH6Yqb+HqD89rzbqwZgbNyr3V0IBWdNxKcGgoOLIOM9IbHHReeSBfSj3zewv\nsN2MjAxnM5OpyTHcrQyyKjdpv+TDc7lMNED9KhbDxNzg2sl4Bc0bCMzr7ergYK5WqS4vFrBm6QgW\n9H0omx0rluJ2I0ulgoHQCbhzg8x8KwClJ6Uw2SmXS/C1LMQqF9syiMFgQ+lzr0DnbTfLD9xzG+Mu\narUVv1lzOsylEvW4KGyAdkduWCwagkjSgyYuNiqNeOLeJfEjSBVejnip5uNkKQfW40UClW/HRvpo\no5H8JOoeOojLUVoxk6+x+ahWKLuaBYLvSMDoasoVjJz1VHvflNE9z7yn8thMfdI8CLcJsmBMM0JX\n22E7xM4KzjL8MHkCBTUkSJ5clomsQhlGVVASJlUImYqrKiNuuFpcM+5OUJay965GXn3iK15fg5Wj\n7Cfpz+xIaVQSRgm/nGil1MwNjGRTw0k3We34yajztje9FprqN25/FMzXEfZeWyLVtizkiH6vmPvJ\n1AWnb3xKKL4aljBGRym2S5Nbu1HjOWTCMyk6rIjLnSOHnR2PHJg9fARECd4I3Kyh7OTgWVu0Vt+o\nLDf1csSzIq1NJtfwhbFfUyJKwCtMJKPtpm8brDyttWjCcRYJbUQE4syppJ1RMhqmZpYrSwuLQ6P5\n3rRUCeqETiTand18doAct9ygs45cgq71lGLMnY0Tw+SbJdqXl+dWlheKhaOV8rLfLDudiszmcYlP\nuOd8VIOATF263v5A81g2VgyFJ/W2SYSg7cvqLHz3cWqQnCqY0fT2OO+u/lUntRtBv6tEFPItCTli\nvsZkAqG6ylpzo+HE7bCXVA7balIB6VdMMAqsDaQgcHhU9Z27kRCNbWrv4gn6IiHK6R8v0BDyisMe\nXt1efO3t9qTU4/rh1qOsUuvKdXqSTIHwag9eDEc5uL3pRhpjd2B6wQj0ob11bKK6J8oKTUYodFKD\nuYm5I4uj45uWjh0dm1z/7Gdcft/OI9UKjrEgIJ5ojkhBQ3bwrpp7X/XB6y95npCnhsNxGDSSyw2O\njqYHB3CczvxRZ/fumfm5+ZlDs4O5kXyOtoaJdpJSf7tZddr1TjoJv5yKZjcasElFNJOVJ/SsTlPz\n2mg6JbLFBCe1amNoIGcil+TantBck1l2ptGMwqhyxpRw7HYSw2Qy6Ua9EUzO0oTPMn1sAIRbAoCI\nM8BQUSCOTnOF+ubK0kN7vyU8xvJKp1om0cQexEeKL2ehNHH3BDwgdwTx8VSW86VxprfmFSrEr4tx\nRwysk0vUa+MX2jwt2DH35OjldBFwn8RfT8rPd4OpBrKF01brSidtU8mfjnRfydYuzXLR1VKoeG6m\nZUm90vP8cFC4ziSHnyBwnib3ePR4GNbbMnBkRL28VIEHXXDtWMCHU2Q23PZPL9fm94SwVWdB1Aqk\nyNAbTBFkhrLyAnlj//gyjkU7FrtGw4guNDxyTky82RVfLZJqModUxkuho4ZZjI9Mud0aivUH9x36\n5je/DS4EzzjWinarTJBlM8BbpORAZMamxEAx1z1OKqx/Jlb4lYrD0EsreOK6dVP79jXuuP3+gwdn\n2ATTiWwuMwipe8O6zXKrgJPRieoCbsV1SqXbqM/azHtxTrYV9YgZRB00wchInQ50cInj+XthjuUk\nivfonJmKixU4Teo2zMMsv1COpK+THVzL0oJ5WY7ISkXcZKNemZ09tP/AnhXWJQ4bA63s1HEyBMUK\nBguyQeuGF5RFwHdEyQPjBcPpyiQ615wWVzKmuV2QIwoPTO3eUXKYMHwkC+z2S52dHK8//sp0YBAK\nYmreryVFsEKJVdzAXQZa335fPBB4dxUacANoQWUU4tpqobdVGrLwMnoBfQ3iCSGjRjujuqFf1w2j\nWcPgbUreyYJCvWDYaBQYuug7EIiSvgceOjDzrq5jzz2ug8INZbz6NZZ7c0Gsw9AVW+1os7tnfFLR\nwwSe33LGWQf3z46Nrr3z7vv37D1wdHEJrk1meGuKqghjNml+QSGWmQqE2RJ4iyXHpGQiu0pvDIcU\nWAjtW+xFmPhIjsmveBVnbrZ6/717ZmcOLy7lUWEdGppaMzQhE88Abrm24mykXUUI/rJfCr277TVk\nXklsROuaLYlYXLuDfHEbpAV3DlebWruI8qSz6BSvnVrXLIrXwRlTVZayi4siEMoM4p5bSiqVOyFZ\nmoHKVCRHKD9Tc0/EaVTDTGHyLtQrSwcO7KqVaeVcatfLLLSokLhaqrnVOkXwJl0+vXmv5miFTqLz\nu30LM7oBUBb8l7q/CMzpwApBkLoS4rONp8xPnxS4u31jH44T22lHiyKn58NVjknVUwe/eE4VQ2t3\nALEzXrPcrCMVHVPFdxo/02oZEnP7ug/HVBVA+JcS50gSgX0zSk4ZhZFmu8rKp0JMjtCUVS3QId9N\nwNkLRtAClj2Kt6aTGYg+lOFjUiURYJ2tpaMsc23viPbQniBJFYJdtKvsf4EDYoEiDXukJ/NkIgH4\nqx7KVZF/KUw4kXCAj6chlxdAqqIWaCQD1/xQVxoe6AtzZK8WvXwEs+OC17T8TGKwW48O59cuLrYf\nenT/sZWl5Uopnc+2CoflwkTi2Yy0BZQr0rPKQHfJeTkmdglbo7LKtUdhfBT8m7KJM3PIv+vBXYcO\nHaYJP5MeGBwcXbPmooGcNRxZ5wvhdkRRWyhWScSerZ5iTD1Kg1wjzNSVjknhY3EXCFhqVTofxJGD\nJQ3nhyfHJlm4MgS53UXPMpOKS0d7UzLLTFZqpQQ2pWMltP9SKbocRBxQXixIKHe3O5iRr69h4EeP\nHjt6ZInen8qy162yRrtE5E00G1qO9qpFXUU6/P9PaD//6UdMRhoCkkXVV/eyNCdAbAwxhXkAZSoe\n5Uw6CL5r14Us0ADAUaoWCSfmpdpJpjPVNrJ4Jo/6R9C/YlihEbnM0/c0rHt0ID8oeQJrRHSIrgKX\ndos7q6KRblDTl2ApHoT+GsZEA862Fql6WrOulZm9wLN0neNoJuZcJCFRySBf51Qqwt5W3SsFYzRn\njUo/kPSBSz6MBrBVZkrlMrZks8e4za1a07rDJOui/TGfKFbrRYQhEsTDzOVDxwom/AAqH1BtnUMH\n6vfc+dDBvYelZB/PpFP5seEzkrGslG1Rnlho5kZSgO60nPDgHII5rr5TXClw0KpagYBtRv1wmypu\nKp3EXgsLICrliLLyc1Be8hOycVK5lUdTt0thyuIjV7wlQMkU3qjtFcuUhFhEycmJtfADhPJVr8B7\nGRnIUB8BK4TAeP/9P60JSC4yQt1WnWmiDn+zLYA6qLyoE9XaqW8D3X9lPLcw+nz8mn6nxGokRGbQ\nto62MokyUYYkFk8kYI5E1LPSSE+LDxONUNKIek4vyYtqO5KEIYF4hlQ8OlFVdQwEt6WjyfCtrkpx\nay3JFZWo/iC2FxVFeqJrrtX/u4EmghdS0I7vZgpa+0JVAr0gXT8gc7nqpI2nKXXV3nyqfmagv5qd\nR4MMlRWnIZYv+KFg0rWekpWQZNjl0D1OJvLZzLAl8cp9CnprGs2WEeZ0qI0jWjb0ZMbR2C6UKmW/\nRaiRT+/fX/3xY48dO7bAmh7OD2Uzg+ecNUkAxqdj4q2mR1jt94Q+ae60CcXZAbFprQSJI0lnkkKm\nA9llV4yxEbeAAgEN2af50sF8Zmpy1LqHMPDiclG6e4SAEDcISxavbop8LjqIlTqkgIgIuDjsPx1i\nkpHhoYGEU6/VF+f2bzu8b2Fxtl4rcxdTrQUZGNsRFrh0ByRizCgXPf+IjaFQH9Y1TyOuret4v1rv\nfqJCsv/LAZnj+1yC6YWWclq27WqsQrqgo0bIfzrVSnNshIliMfH2sjErXu32PkBFwjQox8M0zfi0\nlzShOQY8WdeKkb3UoxvmFdxT1/jwxm7xAz6MSTypO++a7GivL6RrNRnjXDphI18PZQ9FNntO3AsS\n0JNURHuQmmOKhQbeWB1AtRRw5wRddWHzy5NErKDHbP+jueQIKCxhCt4V7zk0nF8olCTylFEfUa2U\nC0DeiaFLkxobyY+ODTOccLlYiH3un34uAF9ucsva9VZM7jTI0/xSq2KRnWxSUbs0XOluIpNXRgoc\ncnHQ1uQLl4EPYZTK4gpzDqtW32FzGR0eUpzRU/C7bLkCNaN0Psn0lQxzAZOCi+P+TReBO4QyCjcz\n6WrfErFWu1Wtl1u10n077lpenqUM5HcRNWZBIeNTcOiQiCCzIxCm4scApBV2OmkZZu25IZVKmYzR\nuPZWVn5Vth6qqT3Bdx0Xu7M7ykr3XNP28tVUBXoTPWDY7kL+hu++Uqyt6YwgqmWaqYFeZd9gVq1B\nGoclsLeobv1dHXwg/VDqZZXvqFtI0ENnAyqsXzHieU5YYg+9uE1wD1k0q5oF9ttkfLX9JTB+6eX1\nAjm4ALcJ/biAYKu4fg8X8TXQlCFwWsjpuMJMobAWNM7yvaxzYA3o4WztE/nMKJG8CV8ODqampydL\ndQK+VpbZCk0YBA07HLp5wZwJiSenpoju6CGLbVx3lqXeEiyBeLUCKEaXtciMy+4iF8tIFOR8WUvG\nWUaw2DBTpk3gX+lF09LmyNo10waW20bDutDmfeGlqsIl75UNl6on1ikjNr12VCawpQwIG0il2QJZ\n00uLMzsOH5g/Bp1mxevU2rUV2thiNPt41dZyqcWSZARXJom4uUi1OEYI0V5rX1IlCQS9YMKZlQuF\nCOb+SgP3SOSJgi2n+Nl3gzBGo1a54ZIAdqiVOZLCEoyTp64US3CYXWSxyGV6tCrtQlLgkjPD1Wkw\nSQofl0BZW9fRBIylzOhc1YWMSlVLAxAnbJjU1NDrKl4hIO7qOugxhzUhDmJ9Yfhpkmw6wP7xkvyR\ngFMQrDxti4l4vUYQVTE48aK4JlstEbGEMRihMPrbImZo2binCSFDSigbDmXTY5n0aDKe50NjCAA6\nMVwzYwsOH1ss1kXQI65QElkp4ihE3HU4BtViq5m76srLLzj3DHaESlMVI3RDTCq1K2ZtsCK6o23z\nSgOyM4wODw2jnTI/v6ADg2gDTWLlIyND3c6EiUngxdvCwu2SIvGnUu5EbApsj3egdGRfR4sQaaEf\nxIbDboWwaJH37rx/2xLqLEtH/UaVrZvwx0PKtlGJ0FNXbeh+EkkIFzwJgAQeDaLD13WEPoWyc4pP\nln5U7WJ0VgfjCP9GWQR+xP2VmXuP4RR5QrZ+wvKQmyn9+56yB4XcGInrbF1kbDswIGKZVLJKZ+EK\n8R34VVQnl0X1z2rBUkOIbtiRpDRvz3I+DEng04j9SuFvGTPou+7qzGSNyYJEWYecB2yCHjHbCU3f\n7D7QRtbuSu1a7GHz4SFFvJB4ogsybLOKBouqV1FWKqUk3L5wDckeuyrsIJ0CJkwLhA8LmFcyuC+d\nQnB2NObm4AtzDsQGMqrVb61fvxbl2kY3gpYaNqzlQFnRIjGl01OWFhe2d2SSGZFxiR0imxONYK3i\n17S3gRiDOA+sWfSYOTe8damMqmpt/x7R+BunuLpxI6dKdI51icZfKkW1UjT+4lFaLqxjSOUR4z1F\naVEI62gMxJXNZBPZDFLf3YXFuW0P7zk0s69ZLnIOKf+YFHSYP+hV6eQDc5KDZw9vlYWqiha5sIsj\nqkuXSUTo416RIfYAvbDDCeJF0ZRpyImWzO8U/CImqosynE653cFMqP+fPLT3TlJH8s24K4LUNKy6\nyHBQ4FQ5J43GojCclot+sVSBC5LKRfsqr74xIPmBK6PqIF3FxxVjFgUbqlQdqQnoKnCVhiWhjNSL\nu31BSMyUnky5PDBHrXV6PWkzIwWLrrwEhO2Q5u75bojMRHsTpP0T5i6qxfer4If0tV6QL/YtojRN\nckXyU4qvdiDhix2Rp0hkE/G0ePS2xzRCRihbYWHr1nWp3EiN3OTATFeRD4GxuzCKHVJKvrZaLlIK\nn54cj9z4xzuMrNv1Or2lrNM/sqmVQmGJsVikm7EYKwNqLuF4pQyM2FL2RjzAvCRwkFKItoh3tDQj\nvA4LKlPepLT3t+qAbZkUIDGoTqFZK+7Z/cjywpHlxTkWWNT6kNvCLnObJeeXzVLt/1kLeM4vHcMU\nPh97wkjkKYdG9Y0Od/3+6iOpuJVmTh5xE9IM+4nWOK1wXJnaaUdTQcg8LdEDE2xD7BfYdWws9aIX\nvSjl3DU0lEcevVRewuc0WeERbyCd02pEQqsnko4L3qfgddIxVYVob1inZ97H8zshgzISWSWSALUH\nFJjIKsIYdQJxyagKHcejsfAEKRGsDsoMJ2vTj6hBkWVuriJ4RphJRhuqQCGSOKBumLVmpa6O2PZU\ntCdAYzsKjhKvxFP5pWVn3dpLLr/seU47tTAz3y4WxrIJr8Gw+apkZKlsodXZOzO3f2Z2/8yy7O76\nwOL1YsrnaOESrclkQpEjqRfiPHnFMtOfVpZ40fj4+JbNZyJ5ToBOkE38uFwoptPSYRET9QsPthcf\nytpN9ni5Wl0TZ+r4Nm4XEz6Yp+Uy764sH9vxyK6DB3avrMx57VouG69Wit0alXwqNDrGF/bJaXjV\n/4nJHKebFPmrGirf06CL9Ga5mBi06An3c9ZPKENammTrwSzG6035E1StLRAAaCxNfPkcZAph7XNF\nU+m4S39ixzl2dPHJF6JHsFhvlDZtXDd/7PDk+LDoDrfE+4SNcAwU0+Kp3A6baYwbCYpcTlAhIjzu\nmXi49tR9JFRhqhd7B4IRTkAcBHzHb4KPBL0jwleN9KRWoqHR95pXrH7U1bY1W/m8XSITpb7gwmlO\n1dCIZKUrwbqZu++uNtd2GXNfiY0MTW/adI7nxFeKFRcG4ESKpC4b9RFfZWFjhCT6a0bHhgYGu84B\n60Sr9R5a0lGBNx7vfP8hG7BNfdO6HPDirAMr3Vs9yAb5gSdyL1se4lgCgTvGBRJaHT/IjQRiBB2X\nHQSRXIoiOKh288Du22ZmDh0+dMBpVpM5AtEoAGKruKQJk+CoFrk5JsUm+0L8lN76dM2BwYjuU3Ue\nntpMfe+/6N1DmmAQzkadfr2h3jyMVUZGP1bd/0/7IC5vr7aixHSp1QidAZpTStFenWKKqtEyF2ls\ndOjNrzm3UFxas2akUV8BU8bux0cHQYcpSzsGdWscL8OIBUnzU5F4P1DouiGzaNUi+z1MTMW7Q5au\ntoX45t3DqQfRvuUK9a5/H+iJBEfCFNZGgFhbhZQFAnUCR9Wl+Fhpmcfc2/Ifm7EeiNsYS6bZmJ5c\ns2H9xguGx7aUqjAdo0P5oWal0K0XIfZ59aLXqkOBSCVotEiwZha6zv4DB/bu3U9Ughkn0ylanMkJ\nK3WBayJPf+O3IQWQ28p4tJYNiej6ATlBEhpl+0Zt9BnFSzeWNUJWLGp9kVKZd4SL2B5CYTERRURl\n754de/fuQQ2dXSUTnxPSuUMKW2wXVqwzJY3sf7XMxZHRKHZVZDyLcjP6cLp+zx3GfCeau989mZN9\n8jrp8+7d/0RSeqrOci8cQ9cfzOAgVmPi3iMMW0MykinRcTvZLa2FRfEugVC5c/xNL6whIegaqOdp\nV2qlfC5//tbGc579zJGxbL2+1GoW06lIrVIAKdaO1d4il2zA3LyX8JOBEJQZaDRYltaM2kMHV12A\nWbplp7Y67AR6coKdMNQJzjra7V/YpvOhzX5t2wD1jd3Q3BOR5Gp7uO08HeP5uKIq6Ac4kOwDHVUx\n8C8976Jfm5je1PKS6KzRmAgNkfklwwOJFo2Uy8cIbOhAzZPaS/e73xwexlAXFhZoBZ0/tlii+VWy\n6jg5ozAit565RUy5XsMeNe1O6A5iK1IQLVi0FejiEE6EKhgZTo+ArDP/jZAG7SO69SXMZPjV0pGH\n7t6+d892r1bM5EmpCA/L7fJKDUkvdvkIXTmJodFh7F4KqcUVZOnl9hCpqlOLRRLBGov7/0VY8L8+\nuuyXkrr4ChDfvtEEq0AEdbzQ0E8QLtagIsCtNV+XAMAac2WUhWikIagD3JYI+hIr9JJj7eTokYQI\nuTqlcmnbQ87ZZ88PDZ+RzQypPE1TZJU0FtdylYZMJknIBq8xQ5+MTMQP+Cm+ccB6ScgqWuK4AXGx\n14bvOmE1VDC6WB/SbzT9VTFnId+3rRHbMxqIWbnlhMH6c02L3Oi+Gp1r766IC0mDurB8tQYB+CaU\n/PGJcwZy6xt12g0TI8P5pUJpuQjknV9pVrOpocHpbCuz1FheBHVnR8kwD764hMDDGZvWr5kYPTJ3\nlI6L+cXlWqOeh5pLkAIbQ/WxIo6NTCEnEiJgV9i2LDwa410XAYwo/5cRs8hg7J6YGNs4NVRYWdy1\n8/49ux8tLM1SKfLazG1oJekATtKMsbxcbPgCGnrpxJARchh82KxVAw/ixEw3QsqdbBTSRieXuGPF\nrEjQ5hMOs+3zQCf2wrghb8VftdCgz7z/+dBq/2troWe+fr+aocFzdnfDmL6nQdcOFUZ7k7I9Wy1m\n4lK5SySExQU7QvWkDERcXFqQAY7s/XTJUzgR/qXDcDv83k/veGhoeGB8nNbfgfljS2NDI+yoMSV2\na7yuXRW+4tgCZPu2//iKw65q5blGyXXD5uje82b/ms/JkXRsdrZVTPvDth6yEukfCmQkThOSj4hS\nidWPfJPzkga8tus73bDkYItF8euqbPasa4qIPmYJSVZMJprzJiFZNIl7S9DO86l0TUBz+iVg6SHI\nj9L7KFNjvSryPpVitRAdiJSWa6Ktm0ptXje1fs0U1f2VYuHQwRmZmg19HB4LopECzXRYe9K2nUYx\nlXCKLiKZ+eYJHimboEqHFu7/0UP79u54zKkUIgNp2AEemtwri8Td0HkiWhNTupNj/QWAg66Ka6KJ\nJnEtHIMg0G8odqw2D3tM+xm4GpHjaVe/1FWfUpz+V+jjTzdAczViiUXCQFb12Qz/9kLddPtBoVhg\nxpTSisTWzdzzg+mQgA6SKxEjeuSURxpImUO8QxBVPnAgJ20ZvGUgXsUH3n3vfc9+1pO5kbQslqsF\nac2U+MELGuS0C0qrpKKRZhonKqWsio1yqCpTFgwl9C2MtGg+8NbyIV3D352Ar+b1icmsknVlOfWr\naKwGnzF1alo38yJ+EMi5jtEEHJlWpb2oFslHoPzJZPC4DARHLbNYri4ulIqF8kz1Ia7dSH4oBTzi\nRJAZG84OsOvBPGc1lmHOOcgHDdK4VvXcWrM1Isolkv62GtVlNPITifHh3KZ102dt2iAstxvf95CU\nP1k9nobpLpKizUZdmuXos04lHPCYvXse27V7+5HZg3614sYPgmXSFlOrEquUhBzMtQRlZKpRRJQv\nhC/umSCDnGErFtx332RgVbtMI8uuK5RrvxuQMbRoBytTx8w+fiAyfmLHu39Cq+UJz58ytf2F8k+n\nzA08imtBvB7xws75ULblBLTRklouvYkjYLWh0EO1VjC1x4Y+FJpoygwm9C29ztnnnHHpxRede95Z\nlPMeeXTb9u2PJDwKHYhJVKiZPOXJF9DLAM3C5mtTdyMdwIbDbEEnmTWV6e4GQKTS+KK9VHK17ymM\nu1xrJQpTbT+cne37PRmIiBuCrSaAHqYl/RmXbnSu7W8h0iINzY4Zg6m46RARVCqyg/T8tJqRWh0r\na5WKzcIK5Nn6EWfj5vXrLjrnvAvPOJsxUBjYCBTaSLzWFV0Bad3uNmPdVpqZmlRkvPb8np/b8WjK\n6YYKxoqKEsxUMlwRIQ7GOqkolaru4ECT0uSOHT+8e8+OPbu2d4orkUyK0Sv5rtdwGn6h1C44rZ6p\nQVvg4B0IiDRG0MzRqiKOJX033Rb6MZBh3HbMUiRKWGlmhsj8xKQ1qrXqTZ0vMEJyYNZQa1fT8VhV\nhbtop0SRLqosYhN3Pw1u0tsZHb8/VnGjbk8w1uvPpbq+d3LDZQ+TPkWTQVR1dXr0IdeaJCywFt08\nGZ0nNqqYtGF8vs1QtwgnrQ8ZXzM0pJRxR60ajYQAG6ZmrMMOmqKGit9pty684MIbb7zx1a+5fnpi\nXKbn+N7RQwfuu/eeuYNHWsV2YqDB12I0fMhDDz94xpnrKYdUigUJNbQ7XKfRi8F70q/ZjCXyniqi\nx5TpLiClTLJPtNpWH4j0HLcXQEYdo6j161BL75y2bsXsIiuIaBPOuq55/e4pxlI0teIlC5tx3OCX\nHYmp0gNRKYV26G4TkIznRYEwHpcZtNEUnpoZHwtLUrJ3ouOImgx5icLRhYeb2yql8paNm0ZHx7uV\nBfY5OcWudAioVgppboITAJraeMGlzIorryxJnpEQNSUICUL66nbUp3pzkyODA7lsubS8e9cD2x+9\n//DMbgcplRT5E8OuIDTm4B0UFmccdcPxiH9KnE6GLdJM3Y72FKrivUXvq6NiToEYB5GZhFCMaG43\nx0bHF5eQUCwBcMIF7tYhFAxMT00xzV6rs/FQZPA/EZk0mZmiTqjXwuPZ0EY2zFPuGNZgdbyanKoi\nUbgPQhXXQg6lP4gyvw1lNlEQ7W8ScxNJn6hoTebzeXrSZaStJxIxrPyQqkqubq2J/LZRLiqdLv20\npz/jHe9617Of/eyokMZETKoK5lJYbDVFO4fAfmp6bN36CZp75bbiC1oO4jyzh+ddbxwUklcntDuP\nk2zU4U91IIciMlqutwwUkmlUEZPH4G8hhavnjgbqHT190wBxsik17mrk1j+eyUImIx2crrXP1PqN\nuxaO2+bvZkV685ui4k/XcjqbHJKLU6omUplGDZV9pqtC/2RFxKSYJZROEU0oLq8ccqxALhVPmj0o\nGwnCEXPVyygjR5Jnr9pMjI5vzg6MFZcX0C5MoSmMtBhrG6IjOUF58f777tix67FtTqXoDmaHh7Kj\nOWYYO9XiQqPpN2QBdhyN++KMdIpTcur0SxuHhkh9RNy92b2Urx2VKROMSSG3dkL23SZql55MXRRV\nMVAH6RJS+qR0avsyUyCd3pxWDkI4jtHqeU+UqB51oyGDLwy1tc4d6SugrFp2p7MqSmGaBebFrSxH\nlBH2p5stGE1fhmLpdinSI2yA+TznjpVzS3gldHzCa8VeIvxs+CPnaPRPWQ9Duff8X2975Stfef7F\nF8v8YKEANICIPcXaZeBWLh3JxSsJr1xKIOKcHUhk4yMkwFxFFHALhaMrC4AEHZM+RlCqUS8Rp7N4\nYD+xzSOnzE1RgWhRwInGXNPrNmpNb8heMN2gR05cLRqYJmYk0HXyV5Vt+pL/7umB3bDzs3+2WUPg\n8IFMPMsQpaX5ogyPT6EvmEcSrFJtletsety6TNLNYHGxSKrhtYzfCoWWFWLZfFrbiPuCKBNNkuy6\nG8thbJEoFadkzV2uFJcJ8rgcrG4BRb73zU9xn9aMJ5v5bGF5fmlfWd4cBVBLEk6yBUSkpwu57Bgx\nGFKjzupqjvRHwwT93aBZU+qzZmeKOSS1zTFoDQRm09g1BZpZKjHZPkoQzAyZdevWC403IdogIjMN\n6AZZUkrIqy7nvwCkrA497vdS/QWgjOp/90efttxajWZYB1VGlCnKeBTjNI8XNv+QPlKisCDRDpa9\ne/cuCVT0Ilg1GxM3c+fsXvKSa9/4xjfiyFkYjhbzW7UKlI2Y9BFAzaB2E1tZWWCwdL1RbjXgnC7A\nmSNkh2iE10H+XHvboQiyK3bKpUa5IOgNVfLswBAbtygf1ysYC1lW1I8rJmPqVDHd6yKmHNYv4mXD\nrLRJwNbAqm6cGL0brgG3R+jttYacbrxFb+xPP+GCfyekQEzbNIaJylcel11Dz7bVoGYPzQXXGovT\n+j8A3VcIjg6MAxHBJXqh67SwTE+mUFfWrlm/WuuIuj0gjnIs8Xu8ysbuebmBXC4lLYvV4iJSm8Dl\njIOhO7pdWT660qgH6NhATkoe+OFqE34E26w1X4l0n3P8sIPV2kREi+dx7mioCqvhIuQkSlcS2uqW\nJybFjjM1vUZyZFdYvmvWrOFJJGKGhwcPHty/fv16GgUxHW6klH/bstIF7ui24wFV7/E+aDyJiH8I\niD06Iq99chk/LIaHjfchpTtE1nhCmXcSpImEUz5rU1zGxtZTniOJNJ1o8+Wi8Uu1riO2bpIK1tR8\n1llnXHfdda997WvPOeccswAOCW4pAsJER3z44FCeYESq2zqsUebhlBvMSsfjEA3xvSyw8fHJuZm5\nZrdMJ1hEtBkdDByvxZVHE7RUbsgOk8sA3Edk7le70UWZNa6xR1tR0K7OPtApRfFojxTZ5xoiAYOu\nN0Tb1+uxShrrlVsjpgvmq9bu6Vx7T11sVYIOuyDoIo+AKeRHk4UijJVFOH2ZgZzEXwjBCuG9kXKb\nUAOpt0Zd6dl0RP9WFDRAruaPHaHwnxsYNDlLpJNiUuQ10q8cSbVeTw6kwKFq7UYq5k5uXNcoDSzN\nH2Eh4KxizUot2NcQymQrwQOIh0rEujHlvsn8264ODod+KFbYLp/g3a2wLPKVGKWwQ+kjhX+bVAlj\nZocrQ4/rnhG1dmqreHcIxCwPCoc6HKY1NTUB7enhhzGXHE/w9YZqw2K3CD4aecI0RgJZC7Xb2ozL\nsgGrEqXVoFp5HHPLtGfDDDX49gBNkB8MTsHQ8ccEIZxISoSZZSDWzMwM+6wMl1GmJ/UKTUUJVzyM\n7wUvuObtb3/7C1/4QjNxfgUdQIJ4r23Dj5IpQG1pzGGLqyk8Y5wqvhTFkVxuM7SLVqPGQHqKUI1a\ne/7YIwwYkXb/WESYzwKrebW6zB6b21MrFuvDI87WM/Jr102kM3GpM0lzB2xL2FBRq22pmKFKxGkk\no0ZvLapuz469vi3OSkheD+3pqZyspjenw9CCPicF5Sz617ckxqnw1juRo7PFh7bNHjrsTE4555+f\njaeGOGCnTrG/Gm3WJKQEOGFAdoawp9xsSCYmZVPakMkyVxYRDhIQoyMTXBT0Dup6LVeatnzVJ0EO\nAGXbaDY3uXHL3l07oWNIh78A7TKXKx0OJ2mpjJp5wXhKeot0I26VGmyRyePPKvCCKoPP7LMhCUJa\nHWQFePvc0SPAmZgIEx1pOeFeViqESYx4bYyPr+VuLS0v8MnT09MohW3YuJ4ffn73Nus1sbKc9R1a\nHvmEzJ2VGQ5aMeEQRUiE0m/V7ECrqNebY9Qu+5UFhSponGAAJeHW+MQozpXXSPANNF6rzCHns7jI\nndBu3UhV+s0bmsM0LrzwQhw5Ebk5cp6HcicLIOKpNg4E/3iY5jLqUlM3kHb8GQH9EC/gGARiT2ck\nT6CwXYPxnBgdXrN1c3T22I6DBw/CrGayCdnvynJVRNAapHd0Wuo8tnlnuVjavQ8O2Zp166db/iEp\nYVFacVP0BvkK34hLanWsABJO5Atqw6vAa6THofeNFxzp4xrYvFXdRb3TeHej1EeU/+iYWqpOStxy\n8ODhnbsOHZ1rrawgXuY0Z51C9cCWres3rh+UxFP6c+Ouln0jMgOihRwjgVlHpKrZpESlgo00nxuG\nEQyQSDwvuhqOUpHphYimWqLQz0jaLJ6gUK6Rsg/mRqc2no/TBSkTqAR5REepw8EQOU+LeK7Issmu\n3Fa6ophA1MpAJ5Bg1T5QMdBxGkQ+y82p6Uku5fzCMRYAzEqUrLl/7N3NZs1wCf5mG9y6dSuv5+jv\nufvuicnJhx/exrvqqkRg/ZcSGHTbbCxP1LtXqhU6PNj4+N4wnhE6f6N2cp7K1SmJJGowfox3sVwJ\nVDB0WmS1ACTHzFmwmLFsgbc0KFcNVzSrKlzoa6+99vrrr3/Na68L2zoBneQ0dXMwDUDexcni/Q3h\n4ZFkcE0iIVeJMhzziRgNlUi0ROA77mtTGG48lcy6gzHpbY8snX32JYcPLx06tFMLUq3CiiBsbOMw\nU5PxdH5wgOC/WisdnqnNzc3mH5u74iKf5ptQU0llmOBCRpsqaC4m3nV7IqY2f8rr47NFe0iOpT3d\nE8YZiJvrtn4xaTQsKlvqcvvPHlxcKBxbkMUJMMt4GsKshUUIjDNMG4LkzAYsupYkTe1yo0bFqZDN\n5Nhca4QejbqGiM2qPoi8ZQImSiRuRJWo9VuaiJAiLBfBoRAWZLPjrO25Y5XhkRGRku5I87YTV3RZ\nS8cyPR1djoCS1Q0YFFbMUYrLCdV4+6fIt4E54Cqm10xQmarBZ8rn6SfNpAnU/NGRHHNaAEWGBvOL\nCwsb128iPiku1/iTSqULhRJRaHkFoRol3vc6f4Meq2g8JNOePD6b3SYo8dhotajwT8yXe6aQTNmm\n2ejbfIVkG+oIqHYcu6KYFPbNctW0UwBELij++zDqwvjSxUWpjMaB2yuCCcdiGvz4GzZseM1rXvOb\nv/mbZB3K90pWq8s9vldEY30dAN+p2QxUDoz4npXDF1HDG5CJa76OFREPbAIkLJb8YF7WSdzNJ0d4\nVySaGBgbqqEmOzZ93tjYt752+97dDFCQSBudzOXlKgxhNMycWENaXhlzKf0HDlB+a8W/5SdQDwoT\nE6Uzt45t3TI6PoyfpDmi4nabUu+UgUs6qg2GlhIz3bxr1pnUtCecOCm05I5j2QvXjdKv8WRzcZI9\nQtamH+1QbHRF5EZIX4RLLXqOPCbFDUIMm1+o7tkNNbY+U8R/x4WVwKwH14dDKypAMVmuu3btmJq6\nvInqQsczwX2c1QBzmb0q/c2YZHZ6pFhoEBEgNZeldQ0iOlZAb3Wki8guRynTPyVsk7g0mYpouYxN\n1QfRamqAxDdPnW5U2Mks3OOK8xGvT7RWnCWx+5YtW4gquUOkntxyCDrr1k4RAywtLeMpRSRsYUnm\ngbUkL1xaWcGUielFSsCXZmwmRobAT2jflk2GzvgEx6y9X242kxWUNJGw1jKNrILdU6t67RC0ktCw\npw2vxMP85OQ4hj41NcXb+XgOHj4dije2w5BmqAyRwKmYKR8IgfSCC8773d/93Wc+85m83ZSjeYGO\nMYOQlw1BVOsz4KwtZ2UZ8ST7hqow+Nj9unXr8N92zHh6E0shtrIYCbiNT8gODOzdw2Pv0572NC7U\n4uyhSy+7cnpqyCBTRJ9Z3Vw63oIhcpI6bLWruqdir+UyEwsbboTqnvSJDmScrZucLVsmxoYHqEd2\nRMuia704Ik3jUGfMmbmbYocRkETsIi3zaKF+CEJK4JxK2WaFh9IubPlG4Q3g7zVdSqWHa3VvebE+\nO1dmtO3ivANhShjJOhtLBOWULyWUZWm2kqLOpo25Z1711HJlkYEmiaTTaFZFFsAnMokODY6WKq18\nbhRohyguk0HVIn72uRdOjE8S0XPRXG3mEt5e2zu5x9KCbeummfhls5Z+sbb3KiEW106YnpEHtRWP\nBI4PmRgfFk1GCW1bGMfhI4fHRibKyr6ss59GJH6gJITwLD9UG1W3N6rAtr9w6KHKoET6MMFAnJ9V\nZIooBoDwG6XpSyVIteyi/aKe2o4gVs678K+YOBG5WlsHs8aLY+XSYKGZK3ZvYKLdVxz5q199/etf\n//qzzz47PGtM3OxMqbAOp7+0sGCjB0I2mH07aQlbhGiQDIoj4MPXrlvHwClEI6TWSFIWi5Md8WnM\nW8TEOegf/OAH3//+9//hH/5Ry6/kbfFDhw6NDg6eeeaZBw4eGR3JY/1ca40GKyhhGX87KiCykBSE\nedroJKLjpBOew2x1EVpDgnyYwW2D2ZXFIkZGQy/6Qsy2zuWZFCU9wNF2TWUAZcezvmy5HXIl8Zdx\nTatEK51mN6uXudkhCcyw8bb08jQoEzOXvunPzDBMs1MoIQZAyY9pPCLby12udmuqQODYWE9RfEpI\nPUBkzWORicnhI0cOElBPTo6ifbt27ZpUnGJRjVrE6MgUrSEjo1OQas45+yI3loQlPzg0KnVWor5m\n28buejJ4wDl5pJQJIsWeEPG1TznVO8Hole8WzG2zxWR2QNcID03FSK5jRqKQoRSQWplIGpF/qmiW\nJBuqNuoocax73OAQtfUe+T5uOGBv8gLiexLrW7BoFA5gH21UDeIWns8OoOWUxzi2bNk0KI88BsGB\nzc8fo4hbKC5ztLbANEwvCjNbiYq//sxnUdJ//vOfj0MjNqLkCYCFlbM22MFk5QwIk1FilSK6wsvm\nRXqiGnFJTHU8t6mmkZ+QSGGm2HqpWNy4caPprPMMelgoY3GK3/zmt26++WYMHQfBhRoZyfMJJpQ1\nOTm9Z+eunbv2kg3v3LV7MJ+LJ9AYEihdLiPT14RkFQdHRjsf9tJwLuNFIEuKSDyDHvIDqHkmV1ZK\nO3YWKW8TnIjIqEBnsGIbURGSd6bHHQMrATClyTVKoMuqgLMA/MCI8AH1JvVuwJn1yx2kQiECyh9k\nueBe4drZTfm0Rsu6JaWUpDplNCOath43SFqF5D46sQDU9/25YwuLywWoDxwAZYeFhaoAsOlF0ijW\nZ0vUjFzMesvmTRddcsmatRv2758pFSv1ZlD9EL/JPPRo7OTZaTbbQoOZ03j3U445UBPsnNLBC8mx\n3cznBtkWbV8Ohjd1Ay6KUWT5Vl5pUhnS+aiZMYEe8KrZRDSqlP8e4IOQhMXi4TjfMOY2xW4qiKp9\n0DZopUxDoCfFqaQ+aFAkeMCRT+uDcAL7xssemZ2RyylJZ6unrIJCfMnQlYsvvvBVr3rVS17ykvPO\nO8+KGb4qLOgAhaZlluryOza32gYocF6sqFqtbjBlOATLohpWmCnqcPBsKawWPoRlMzg4zDOPPPLI\nF7/4xa9//ev79u0zfyJ69rUa+8/8vGjE8gOzz/mbPO9f/uVfSIuvu/6Vt9zytZHBvGbMAj6bd5fV\nrtPrDQKKRBey+oDiwDiJhXmJlklca1UQk7hWmeT8knHR4iQ5wT11OsfRrF2pTskz7AOSiviUwx2t\nC8vzKtFq2ItRtmM2gAT0s+uYoohUkXg77GUuAmuzB/hGbAyMdRRh+VxgmQudScjTLSkEj41ln3T5\nWqqwa9asPbD/0PnnX3zB+Re/8AUvodAWjadyQ6O7H9u5c+eusdEJc6xSK/T8k+uJq+l1PDb2eLx7\nn9F7pwt+zNwlEqhVdDSm+CRfua+cEwdUb4gehrZ1i8XH3NUKvIGPauVdEUy2iQk9iwkTCTP0du/B\nz0CEmI4xZMxhICuFiWPcROTr1q3lZ14JqEL8K2ycdkOHk4FOyLK0cNxO4YYbrgMjf+pTnypBsLTQ\nSlDUKFcNncSIuVssX0zWsJoFiVta7KZcZXWuvsQkkiSnQwaOFd0MauR5fiB1MaPnBbjwW77yrTvu\nuAPukCt555C9bO3atZRdP/kPHwfU12EQIywkXo+53/7TO8CF/vVf/5U27T/6oz/6wPs/mEigrJVk\nss5QnnxXiEkZkuABccPEZggYYvSgwAP57P4D+x7beYSNcmJ80BaGBotNzyT7dK5zs5kPyg6mpdXt\nhKQgPBfrQc8OYEfgEQKHuBMPanZuPLxBWq3tqAgub6GzB5/FdEQpGNdrSl5qBw1cfjDKKmI7tlUk\nWbY4a9uvqDJddtkF1NfOPffcCy646PzzLsDZE++Rrxw5PDsxMcmb77zjbo5ncnoKSxhIZk85NsLa\naE5r7icsjl9q7nwWizgl01897F5I+vohKEZafVEV0DvUeqQdnep3oxEPGrr9sMvL2sSMDm78wdCL\nmz31xv2t6u3rWA7XbBFrIPnjb8B+PpybjZVbrIJ1WjDtq70a7M1rzjvvnNe97nX48snJSb5TKkFN\nWQ8hbYFDx9r4OlIRWyeaJEhAL+iKFs54MT8T7ZYLBXJvTXl9q5XavmSnZuvEkNbpNWsgw3GEESdt\n3He9JSZ4L4n0RRddhONiwyFKZk1ivizgAwcOALotL62ccebme+65h/v5ne98+0Mf+OAjjz568QXn\nsdgJsrFCBCQgmdqFLSx1dMb8yPpN05QLDxxEb1AUKWKqEhM1BpFnvllVJrXzQIaGxyxS71hgqd2V\nkp/YMHFibk5nZaUA/aknbSyldK/nJIeHU6oh40FkIOpD9BNbPHq0FJZjbeOQsTb6KBRacEbZ1s1L\nBpkx4s4yUdR5/etv+OQnP/7oo49ycxHmJVDmXoBwN9Rb4W7YHtkYN23a1Ky0TrJYLTsq2eYJm7vn\nt/u2gEj/x+G8bVQq5spFxPrx8TK2yOvi1O2WS8QCekoTiUrHtmXQrp9WsJlbrj6sbZC2nm0rTDED\nncseiBu6f3iCwEGbN29mx7cBfUePzmHls7OzQiJv1qwltKkRs8YqHgvj6quvftObbrzqqqtkl+8I\nyM28vh7V0Y3Fgro0z9dQmNUH/1RERRYJblgg/FrFmI8hw0zbIMENMkb+sdKBuZZbb72V3xIgYcEU\n3XDejz32GPBlcaURiqD3mC3WCtg1OV9LnU1hnQ5jmKbWzv7wIw9hFiNDg6xwzPzeu+767D9/+pYv\nf5kEO5fFQXqKxKOCC1Qi5pUbcsYmx0Cvjh5dPHK4FROLB4rPED2LlXY916bLJ4o6dCgaLloRUfZU\nyychQTn4Jm5hfFySHy7p0aWG5wUukGyBgAeQTHKniGhd4IQVy5cFPz+/SN0innZCwQ+/N6TMqDvc\nT+DNoaF0sVxPMkc3meROFRYEa18pFZ/33Gd/63vfKy8tzs4dBi2AJWo9gRZ/Igszf+zYz372szXj\na/uHL4WhSlNrTwCRw78AmTlhpEc/4VM2I133mh3Fw8zyBCmVqFLHZNyhK9ZjKl8s2kwqI33yilSY\ns7fgmFjcEEArqVrEYgxynheIOo23GKY+ddZZZxFI8HYOCQPatWsXhRWiYevtbyjOyv0wnIRU+bLL\nLgNXuf66lwudS0e/S8RdqRhZKJhsrLmELQyzYKbsaCU0YxgiL8Z9wkyxS2EJ6NKijDsklyXebKnC\nvYioJVMPPvTQ9773vW9961s/+9ndhBwt0Vwn6q2wF1955ZV33HEXMcbw0JqwOqtRn5SuuCCUvWzQ\nMe3wViALiMpR74ornnr11c995zvfOTY+Pj935Nvf/vZnP/2ZBx+6v6nxNF2WYCwhcbpe8QaH6P7u\nlMqdwby7actmPDQ73tKShCJCeutio7gJjywWrKDt1yOqXJmQgoaMr9FdIg4aLnTlRoPdhmiKa3ze\nORspJu7Z9wBBDdmqjOUSS0/ZEGC+cW5uni3jjDM20u2JMtyBgweLRcBKme82OppUSqmkWIuLjdHh\nWDizyfQktWqZVAVfCVe279yVTsSm10xu37v36MGDxlPKiTZJy3yfRVD8846f3qmdkGnZhLsCPJgb\nlVUhQ5tPb+4nB0DBgMKgoBMMTw0K8spelP6rXp+OHQEcf/UUIvTeFEqOM5gbVPgv2tP2INUT8jd3\n1+gGIWdLND/gf8YQ405riJLFyqnME5QbIi6Nt/PHcOSE0Vw4zh+7kZCa1i1d9Nji1Vc/5z3veQ8Y\neSC426lb65AFcwYhcyLGDjAQqT8nHkC4Va+drQrTk+KCsiRkOVXrHExApqfyn80em18gFv/qV7/6\n+c9/XhrNVcqLy20Bie0zHDasv+c973n/8R//QXcL+AwYvExok2BJYidOjRjAroDSSGWFP+tZz/qN\n3/iNy59yKXsCu+hXvnzzhz70oXvuuk+mNEeDaQwDadl5aO4mfVIg1acjTXWhdQqPRyiCYx6lzn2I\nuitpdR0TccbHBmiWszkoyQyESpEiszHXavpy++qVKusETngwomtYpjs99amX1ymhN1XKBQ3DJmMP\n6zJ5oEvE6A8NxVXAojs4FEfXjhcdPDhH0x60IDzJ+IjMf5YpWvn8/HwR3SFRj/Mdw99iyjwjQErE\nR9Ub1jEMpAoQ3y00qkuzs1YJIaHX8px4NM6XkBKJpfvvuIOo74wzzjApl9CjsXU+YXO3ldSvAWtZ\nl9ZHuhY5eH3xPWMlLYTlZitG7prYjaDs1bK1cQhcSjsaIXWjRtm1JUq+Evhy4znos88+k7AVm7AN\nBBdODEcOp5PiugYgCg+iLjdY3Fsmc8EFF7zjHW/DxIlzbCOy71IJkIDtaIvKAFOzcgNzrJRoVAIu\npe1ZxIWg3ZZjCIur6yspNYXxxjRL2bF9+6c+9akf/ehHO/ceMLYZ65PPFCR+ackCHjNfnqfdBqIY\npwvp4N///d8xUIJOzohQnkvE641pzLfzxhe96AWUtMCIOE5ODUyJw/jgBz/4D5/4pOl2NGoNoidh\ncyP/DTCZFnIe+kBNUWUSe8Wg45IvQtShbu1k0s66DWtZP7iJI4eXKcsQZ1crgGkw9YfBuG1bSGjs\nLvNc6xRNndGhzEqhxnux1EHYXGRpmSTXpCY9KEzmXJK7J/ikYeoOVPHcQFQy+6rkCdPTNIPmuE0z\nc+KYlpcJV2TIRauOuadNBl4noET0rAeESaHrn+mM3Fbk2bNpoUevFIWh+OD995578cX7duzA13Be\ntg9nhwePHjqUZIx6Oo3Lu/fee+HbWjGRtWqB7mnN/XQPwkvLLcLt0ngmomftBAB5TBgaCcNJ8J1h\nummUsm5v8KrRlUzhKay6g3Vg2dxdYhWiUkMYcLvEKtwe3F6xtGKppOF60B8E6HD88bHxN7yBtPN1\n559/fkzINrK1W3JpdDHYl1rAivYEsTqmL2VLFyu0I+TF1sHU0oflx8Mjowvz8+MTE3t27+bIAQpI\nvLjNxN/f+MY3vvPtfyuWQLKTeM16o8sakxw9kSAD/shHPoKNorrD2V1++eW2+e7evRv7uP+Bn19y\nyUXvfve7P/nJT9oK5FpptuqzI+H7ie+5nQQe3Lm//uu/5lIQt7DYtm3bdtUzn6UNIpkRzSIaNXFg\nUuf32sEIgSDajkM90bUdVNx04I/cJ7LNTVs5Tuexx3awERLiawLTDstV0vUgQw2CgQjwuEEhKd6z\nTuACEaZjTHgBfDlkUHYDzNdWWltKTlQt4g396oTqNAET8MkEn90IA2SKXHYWCIdBDCitj45vblS8\nVTqIb2W4omTDDSPwsf+MDY8Y8xQJyP/5t3/3f7/n3TOHhADHpc6NDR/et2/dlk3lhWXbnLmYP/j+\nbZJza34lzpGB40/U3L3e0PHV3LHnyxMGwomuQaJvOIRR8Iy+IoPew1BB00exVII0LJt0E3jkiiuu\nwGNZDYiMc+/evVzT+YWjZn8K8kiUbxAH/3z6064kIn/pS186MjpqaW5AvZLrVbe0XcTPRO5V7J49\nMZAgVJcgV4ogKZu1AllIUrDLJOm8G6UeJAowqVRFAQEhJyUSa9dueMfb3w5YzjNEmGxEHA/ueWh4\nArt817veBTrOB3L84QR30Ei+i+8l2eKHf/qnf2IBrF07SUjz53/+56yfpz/96ZwIbGFLrd773vd+\n6UtfYkkKyaLHF2ogmhWNXfXMqx7Z9jCgqpyahm0xlQezyUuygDtSsOdGDQ0PKgUQIkNX8z8JzMo1\nEWocHxe4FjSY3RKkih1AKNl144R1TUJGpfMlamVcBiQarO3CC8/n9QvHFjtCoZFX6YUUSN44p4Yd\nHzs630v/wg5gWW/nXnzhc5/73G9+85sPPbQDjUuWqDTElNi4Eq5vg818+xBFe9k8hWPCThrM3skM\n8E9yP9DqF7/4RTd/9St7dm4HiMOXbdy0Cd31zMAQ5CRj4IHh3HfHHcuLwlvRZr/Tp6qnm7fKYpWF\nomWgeK+ZiqMkbAr5W6bsbmOB3ehxo13U7lu2jrnl4OKKp15APGr7F54PLw5eRgIXooeWBrNDWQx9\nzjlnvfjFLyaQvfjiixNS0GCYVhdfq+DPam9eMpWwaJvlURU1C2GH02DXGySYstDFjspIIP0Jd5Cr\nCFM/g0O9+eavcBv+7M/+jAMjIb7ppi8QUXAROXKCE8p7hr6nkrmLL7kQg+A1iui5iupIKiKhlGbq\nfAmLmTyEKH9m5iC7GV/NguH1t932w1tuuYW4SPGipN11C6usnkUeiLM//7xz3/TmN/3zZ/8FPJvN\n5OjsrCQVEUWxnIhtm6qvRNV9UDLvetMMTpW6pGuZiz9z5Fg2m6Cmxs521113zc4ukW6y6pHKYsRQ\nTKAFfuBCCZY6lM9ZOHr//fcTXRSXmZfmrJkaVBfWVTCgK+9NOhMTwxjDjh07ZaCAaN/JvDEdLiK1\ndqow4CqscNzBu9/9OyMjOSYNTU1MGPYlu660cfqBTC/hcVdH/zlRtSbRON6wdiNuRfI6vz09OXlo\n9tCx2RnMCrgTTk8mmQl7+dESxInOHzny85//nNhMLP6JmjukPanDRQIGud0JDo5L0M8jD98OQqID\nmqVnB4PDJhQanwSasEonL8N5B158ft7OxJgquGeM2Gq0vJdWiXe84x34BjMsE6wrLxdMqsryTpWt\nkfq/VUxVsEWQPiUODCqrKmEHeQL5zOrMvJKNL6ZAExslGc/nbrr59ttvBwLnFipiI5/Jb1/1quu/\n8pWvjgyLg+S7rMjPNw4Pj1lSodLtwo0ZHx+TRlXue7upSYs4gKc85Slvf8dbX/fa13HgREQgaB/7\n2Mcefvhh876c4GB+2JIKoyUbc5MbNr80O7VmzZe/9KUrn3bF+/78fX/xvr90BDd0BxQ7wvAEqPUd\nE69TzQydIgYikkxIM1GtqQl0wsj+ErbF3A9/+IM79+z+2c9uv+uuu6EUjI2N0nCTz0nSRdgMsLu4\nWMumnUsuuRia2g9/8KP779+Ry0puw+2CdUOuTOgiJYq2RDWsGaR2NXqFAyvN1J7KneqemVis1Cl1\nE/XteHQ7t3vL1s3mMeNymtGwXpHWrZUfyrWm5oQgezwjLXw66kNql9S88COF0uL2Rx8567yzHvj5\nPRs2rIP2BheKY4LpQacCrcGWUj744IO/KHbvV2bsR+IZ6z6qD35e0YdBHP3jTcLoRRHljskN44Qu\nvfRSyB7wfrid2DFR6WM7HsWS+MEWg8XKtmqqqu6H53vDG94AN4tNwIxSfqXplOF9TEc1K+81BDat\nmqO+oY03snqkAerSgBxNWu5hwZjTY6SJY1Z0ctfOnd/XBx6dCHt0bBqbsPZ7Qzx5JX8DdV977ctg\ncfH29es3WCJh/Wl6n8TQqfWg6qjNeHL9qJVeccVTnnv1s2nhM22j3/md3/n8TbeYpzC5JaOU88Ol\nl14mQyOE6VC3rl/z9E68QzGLlfqVm29++cte+sEPffBP/vgP8Xx5uI5avg+Ep03FnRyJdDESlYWg\nAhUyVhKCjV6fWr1lVcOFxcOUnHkPO0ytXOOO/OhHP/jJj3+0b99hvjCdkeWEWC/Z5/OuvvKLX7z5\n5S9/xV0/u7vV9QeZyp7RQYht2cZNG8XGznBpicAxUEZD04apBRnRPY0N5EsSbDga6e3cvHkL9OPR\nUcEnAJQ4YKJF3su+K+g223UizetFaqGGgEVC5TOiRo8hN6zUixGBs2Mf/dj/euNb3nRw355sMmMZ\nI8Gn6v07ppnDBd++fTtDMSZV/rhjCDorxorengaCRt7JpGU5YjdS/G8FFBHVz4j1EPfAoytVS+xe\nBWxTZO4XXHQhlkreSYrD98Dpw5lh3w88eB+fZigNnyMyBOqP4edjVXiR3/qt36Iow2F6Gs9YL4XF\n3ObLDULxFCqxjhCrZBldxI6Hg+R77QWkffxAsrW0vEQhWsaSSTVA0H3Szvvuu48g4Wtf+wahFAGi\nASNaT+1i3PxAxMLzZosYBJPIubsvfNG1WDxfxAbNW6C1+FqGs8SAI+WWcBEIx+lvAvg3sWV8BNft\nc5/73J/8yZ8BRCqxkZH2TRq/IEWjcGs4Ka/HCsGUmu06iTgtUWA4aA0Y2sMJkge/813v+ta3vv6K\nV7yC75IJ41nox1I3wL9wyuIINOEJwmjH5xpTlwR2l0x3CDDNo0MczJTrye66Y8eOT374Q3feeTeZ\n6kAmSiQBPCN0FKn7RIuVLsSvq57zzK9/41sf+/gnfu+//XeW19rhvFUqhoYGVlboosiyoVoxjlUw\nMcbgizHSkoX5Je2HggHr0JkNFLq4sFxvdyHDvfQVr3raU6646+f3pEV/Pd5VCi88bcwUOTtmV4dS\nFHyLnCDVAC27CuQiC0nCV/R53njjG//fT3/q0MHtHM/Q0AjWy0VgZeCmgHg8ZeczGWXUvCaGbvZh\nS4FsoddgL0opOtVaau9RN9D27iEbTdsEytVyXEqAHTrA2anJugDICQqxe94LrvLQQw9hSQV9ABpi\nkYZ/C4VIH6AxROTvftdbSVhjyveqKz5oztimKnCSEgFr4MHxiFnoViWdncShKlNqobmyIAfqShaw\njgRLQxF/5UM4BtuIvvvdf/vOd77z0IMPa2NeVxH9iFa7BIIAH7R0gtfzdv5pqS3tc2CORrIDKCTa\nsf3NZr5afswVgEr58pe/3JJs7usHPvABnieO5AVsHU9+8pMleXBT2qonQqroxnCfWAy28+Bi8O6k\nj9x7RZcFmJueGrUdn0Niub77t979kY/+r7vvuuuKK65UrGaAVJ67pq3iJTYQw8eKK2UFPYTcNjs3\nf+aZm0Bp3/rWt15yySUURb54002EUmz3jUYXpBZD4hZwX2YPz+EZc7lkW+51Nz+UK1bKtbozNjF8\neHb2/gceuOqqZ/kNKdDSrWUttgT9krO1SDzYMDmv5EA2R05h2jLCWMwkGFfHwUxOjDG4jsh+9uix\nkfHxf/jkP/7e7/0eMKhGuJMvf8VvPOMZVz7rmc+hedLyN7NvHNNgfhA/VygW2DlpJImpINcic2Ic\n58ytZ27f/SAxKFdv3Zq1Qb2cToOxscK8pM7AqyOGlEdVV5sgbEwfCoRLo5o5qpBAzKw8gz4MvlBo\nVnrvuXmAKk960pPWrlujWhpFaAxYOWLbeHTcOQk+R2wkcl5w+PAhvo6rTz2fiJxd3iiNfqdpuLth\nLxa28szY5GRDOejm3YNULBrNDQ4Z54wPt+KURnXxcqlEHNNUs+DmSSw+I4g186JwNnhclt+NN76R\nT0bFQVJAVTXF1NgVXv3qV3NgX//aN7X1VhgExBXSuSMIABIAPqcDpvSP//iP4J44zT/+4z/+q7/6\nG76CCs6TnvRUHPmNN74Bf/rww4/iODF0HCe/5apyWThCDoD6CG/50z/9UwKMtWvX6ezBJv0cqqYv\n+YPoP46NzS8enZqYWr+B2dDzJj/WbFSsmZXXcJv37tt7zTVX/9utt7KwlXTpUWgONOL0Af4uDIKc\nVLiIpl77mhve9ra3gejRnkx97obrXnXPPfdql0/UtCTqCkpOTYyzodGWyHrjEilC5YpAr0yrRxhC\n2jlFsbTRWDs+gVkP4+O7wn6bmVnMZejGyi0slGWkqZDLopanAllyYLVug/Oam1sU1V/Y1G3vzjt+\nhj9iv5VQqlbJK5YQFVYzE3Lr55x/ATcO0FOm8xaKZH1LiyySVjoVeHdqVVTojYnUEbFBjzyQO/7Y\no9t5FwfPZUmLlEvEOvCy+YE8R2CZHICOgRjC4W7VbR+xWMLy5UqpaJs1rF3GkrHhXnPNNU968mXG\noMB/04JFkMQujGka4zdU/mdfZlGCT1M8eue73v6CF7wA8FGuJjJwaN5KJ2szP5C1NNSQk7C9w9pb\nbZVbzT8AWDJZAyjDyMpyAC69q7FkRevz1m3EwMG9+/aw5+D5PvzhD3/2s5+9/MlPxfiMHqg1jixx\nAtO58e6ci0ThnjCQSbjJUFVjxvTAhEb2qle9AgiFl2kLdjCboFppf+ELX8DEf/qzn2r3sg97wjg2\nUmusVoYGRRKZ/QGr5RhYKtrl6CkvKkuky65iJVg8Foy6884/B2yEZ8h5iLjyubQ0Jufz3Cbbljk2\n7JhrLsyz6Wl4sEZKwdcSBA9PjEMNejF70AuumZ6c4to++sg2mUieSl5y0cVC18MkY6o91iC7GGcQ\nEQIiTMqZnuatRFDLcF1iMteTcVpZ4v9yrUrz6MJSmSW1a9f2zRs2YluFYiWb5V531tBfVyxaiwnO\nioFe0DiIrVnV8gmIrLTp6mmz+3JNuPLT02ve/7d/xxGCBLCYfvKTn3z9lq8C74Kycxb//Jl/uv4N\nbyDD+chHPgomogbgjI6M+j1WrM3UCI1BsODiAv/8/OdvevG112KEJJkjI8OYIn3uEv1ec/XLdGaY\ntGNKjTMRteYMLrfafd3CJulAa0tmk8/mzjr7TAra7IZYLa8kYAXD4KPxYSDlmILxsVROLG6BCsLk\nJACvee0NANJsoI4UI/iuWF1hbGOk8GNCh/VBUXHE+oVJEjaLmPPGCiWFIGnTDY5jWy6UhUUN/Kw1\nI1aI4So8jhw+zHn+9Kc//fKXvwx/kN9CM7zzrjv41V1333Xllc+YnppmvbFy+RwRUOgKgxf9Q3w8\nPzCNSiy76UltL+qo2noVqJuggpAKuweIfPUNr+W2HTkyx7f86Ec/JsKZPXIMDlxW1kuWaw1foFwp\ns/9y2DOHZzZu2MinLSwuDGQHHnjgga1bN37kIx977++8NylUqijVK/YNDkDrTUaZrrITnnnmVsyO\nO0L+cOzoYaBP1qRtrdgWUSgvXtbOElg0b3j9a9lUuXpk+RSnzrnoIjHuROq2H9z2pS98EQL6p/73\npw7PzOzdvev6V123tFzKZWJcwKNzS4RJTDyMJyX5kSJ0wxkeSoWgnlbpOyOjGSLwlZXq+OQ4KtIU\n8T72iY9RwGaL/sEPfqzhxDq0FfhAKTsSOhLuR2Vvkb4Apv6y/cYELeXKPOPKp1977Yte9/rXVwgE\ntj388Y9//KtfvoUQCLg4qZKa8wtL5JiveM0Nn7vpph/cdtvVV1+DVg8GRu4O8yxunamxZE4LkVap\nxLvDCOGb8vnce3/7Pb//+79/8NB+nscduFraj4wMT9uFs+BEqXwSS1gfMcGFKbxh2Xhx0MPNmzYp\n4tbAqxGuEIOC1qGRIq0Vqnsoy0PmIXS0Mt++/LJLiVVuuOEG+CSS0rabfk8NGiExPtyiYYt9NThb\nNoDc6rKhClJ+eFgEUJQdYfGVseFRswsFkiK60LmXrEAi8ttuu42rY3zxhCkWkeNnUw9vexgnQWXn\nL/7if/BbwjAT341LCFTVLUIsvpecdOEPW0GZY1mzZuolL72WdmzCNmie+/YdeOUrr9u1c19VQAA3\nI8V1AZ0MNGQtcbJcn5XiiisqA0nLtvHfygDpbHtw24UXn/Fv//a9F77wWhYA9wl/LUCQI6eDMj9P\niuv1BJmBIEUqCf7NCzg8Lpdl5IzSIg7hdCjiYgFwLgJBOcEVWj++/cef+MQnvva1b8MDI0IkXcXt\nHti3j4aX195ww81f+qpUiJJRVELZFGV771SpKKkoNFmTaAYCu5NFSBTaBk5okBFJCid9fsJ0P7pU\npNxD2ej/+f3/9v73f5jtbGJSeh4KhUoKnhl94m5M6+KSN9MveemTLwWEuOqqp3NXtz+y7aMf/cgt\nX/4K9ISBtDR/aJk8YakapsyZzivFV/AM0cKWjYgr7AYF/q5Oz/WMUi6sGOniq4nyxewR4pZrrr7m\n27d+d/u2bQM5RKuBa5KRTRvPNsl62fclPJIEiDDCUiUKQGw0T73icjYsLrEUgPbtZyNm68SS2LoN\ndrQ4G3wQq+GNbKlgBW9+85svuvhCR7uZ2j0qrwSHzboFOZxeVkWOSj2snZOEtsHV4TwVyRFKjFT1\nucQak1jpIeQwSv0ZMVjlTtL3iXOFgsIixOfxdryjNfVZI7Z9e7FUYkVZDYhd8u///mM8f9ZZ53Cm\nd915j6rnZXGx9i2EXhGt7V/2pF9761vf8huveAlPZjOZo8cEOQXkfOONv/ntb9+K2NX6dRsPH57T\nTu22UfN4JT6M64ZlG4uG8+IF1jPFuUvZqF794Q+/A3KFM77wwotZZlOTMG2ErGbEB6lSVco4MHZd\ny4zpILWAkI4W2WwF6Cy99KUv5lw4Bd3TY3wjBSyQn1tvvc0EI3IZVyEHqwDK7b7n7nvPu/DC97z7\nt2+66aaVQnFyYrIkQ0lhv6HMLDcxm5HttFKqkIlOTIyLa3SiXJnFYmtkGJGpTIXAq97qJCBItrjj\nhw7s/9fP/TP9MdQGQQ2oQmuDMpfRWTM5+bznPZ/iN7ZEFYyI5S/+4n0/vv12qud007I3ZzHhTIZQ\nG7tCaceY7lK6AqBCO7qFPaS4s0+78sp1a9eCzNRUX1YT/XhbKA9B6z1GCNFDCwLzJG9sxQSTNS3P\nu8q0i2zccAa33zYsq/xddNGFFLeJVYhxaRzGMtgcsSFcC+a+srRsZdFQG0NqlsCOqSQRDo6ctk6i\nFBP0F62PTtf4hjqLIlBxoDpFPDN3+JBpJ/FpVsmnqDE4OGqhvO0qacXCjRTA2XR0hquhLnwFF/TR\nx3YJa+U732GhGo5kFQN+9eu//uvcQg6et3Oolpys37CBCJgXADuyjrg9n/70Z5UUsHZ5SeCXZQVG\nCLiJpMFV3vyW1z/rWVeRj25/7JFvfOPrvOuv/uovMWIqTv/jL//mU5/67MT4NDEOnAPuvQyf6Qjy\nY6vFylsYXyhoyHUQMFGPxzi9MAqhT3Kox44unHvueQr7Dti2RovTkCpwsMfin4rCZUiSHNidoiiL\nfStH8kn8zJpnwXMdvva1W8jCFxcLuZwkOYloWwFf8SZZlSDnrInvIc3/709/hlT7s5/5lze/5TdB\noDkYeJoRX0BS+o5hk8mGrzgfu+mGDWtYq3TQgYNQQkb9jCIYgfFyw4cDwxX70pe+8MpXvHLbtgfe\n8pY333ffNg1sNr70pS97yUteRrFlaHAEm3vwwW3Xv+xl9HCj/Ts5NY5Ej04WCZrcib7Yh++99z6l\noIpJCCFM1eA0UXHe974/+5M/+ZM/+O9/9P7/+Xcgs1rda7KuDOXDwKRLJhLVrsgVzJ2Lj0dutBrM\nvWYYnqxYmlrgunCz2dO56ATWxm4lvSUjBmAmIjf/FMQPKZcjM8olT4LNAbe95vrrtpx5pgwiIbqo\nVgz9sYAP+Qg+LU/iKCNyE9ViyZrKjIIsFYFsxjQGEqp/ZCNQzHlbzmopIHeL8xcQs1YjrQHOAzvD\nlAvFujYipQyO5JAIbd9445vxE6xDYtxDhyiPCgrE6uX8IVQSa91555033/xFwjPikz/8wz/86Mc+\nZsxvHtSMoGe99a1vv/zyJ0GTuu22HxOj3/q9W7XjwzHuEUVQXDKRzxCKyRmsM21DLIBq09lM2LZn\nOToR/1OecrnlA8R+pFy2H3Kd9bwEYucrfvu3fxvfScmZQ2Ll81stbjQtBLIUiIszNTnBIkRU9Zrn\nP597wBa/c8eOb3ztq5/5zGd4vXhlyckiBm2JHk6tyAHrzwlekJYOFWH1oe1Ta7Tf9a53/P1HP6o4\n5jPQLZTynC8CZkjF6NxzG/7cseqebDgIQne1doiujcJ8tNGT4vFfAJ8/+IM/AOCamp5m7LkOJmEk\noFTKLrjwQhrgMRvYe2xTEG2Ekp5KIvljmoSEuBirTXcUSJAeGR2PIxacYNwSgY1Es0fnl7ZsPWPX\n7t1333MvMKD4TXKtrlQkgyqbXihr41I4yDMJcnwpMCtRZeSDf/sBfANXWenIBzEgkk68OCZuMXQ4\nb8jceaWBhszwc57zHNA6Mr+ehqNT1tKgMJaa8FEzXG6LpdI5qg9ErkJOBPmHlcbbg+4nbdNOMHrO\n0wqzEss0fg2agGxMgHl3Y3XyIWx5XBdYhOAqWHBHQ3fbPbASTJyv27B+Ex/Sk1T3rCJm14LlA4cW\nrw9WAQELOAhFjf0H9sJU2bxpK9sa3f54R7qev/vd7z76yGNYLlCAcm9E6JSlxfrn8MDaL7v014CL\nxsbGIbdQLVdiHGoijZBvEwqhASGz5FiHXHQjrhn1UullrtXIgGj+8i//nE2D9IDDs3yGo7YgkDSA\nxYk/uoJW2nR69siMQKKRCMuePo/CcumsszZbpVlrk23ra5FKRSZuQgkcFNu4ckU7imIl5wWc8H7t\n1y76+X33wejC5fGlXqd5SnM3EisqAej0OjIWQZoexJIGMgZsvOlNb2JvJ5fmaGFD/M3f/A2+kowo\nptIAOIjLn/IUMHJIODS6S/c6eKfHXCPHzN1iccttICO4Sj+W+E3n5VCZomsxlx/C31PbeeTRx/Cz\nbBp4ZDBTbnQumzatFOuJsWY3owLwXdAW7r77bm7B/wEgavXKyD18QgAAAABJRU5ErkJggg==\n" + } + }, + "id": "80e825a4-1a64-4889-91e5-332ce2d7768e" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_2/notebook_2/error.ipynb b/tutorials/module_2/notebook_2/error.ipynb new file mode 100644 index 0000000..668a0a5 --- /dev/null +++ b/tutorials/module_2/notebook_2/error.ipynb @@ -0,0 +1,115 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Errors in Numerical Computations\n", + "\n", + "In any numerical method, **error** is inevitable. Understanding **what\n", + "kinds of errors occur** and **why** is essential to building reliable\n", + "and accurate computations.\n", + "\n", + "We mainly classify errors into two major types: - Truncation Error -\n", + "Round-off Error\n", + "\n", + "## What is Error?\n", + "\n", + "Let’s remind ourselves what error is: $$\n", + "\\text{Error} = \\text{True Value} - \\text{Approximate Value}\n", + "$$ However, often the **true value** is unknown, so we focus on\n", + "**reducing** and **analyzing** different types of errors instead of\n", + "eliminating them completely. This can be done by using relative error\n", + "when using iterative methods and is calculated as follows: $$\n", + "\\text{Relative Error} = \\frac{\\text{Best} - \\text{Second to best}}{Best}\n", + "$$\n", + "\n", + "## Truncation Error\n", + "\n", + "Truncation error occurs **when an infinite process is approximated by a\n", + "finite process**. \n", + "In simple terms, it happens **when you cut off or “truncate” part of the\n", + "computation**. An example of this could be using a finite number of\n", + "terms from a Taylor Series expansion to approximate a function.\n", + "\n", + "Approximating $e^x$ by the first few terms of its Taylor series:\n", + "\n", + "$$e^x \\approx 1 + x + \\frac{x^2}{2!} + \\frac{x^3}{3!}$$\n", + "\n", + "The error comes from **neglecting** all the higher order terms\n", + "($\\frac{x^4}{4!}, \\frac{x^5}{5!}$, …).\n", + "\n", + "Truncation error occurs when using numerical methods such as\n", + "approximating and calculating derivatives and integrals. A\n", + "representation of the truncation error is show in the figure below.\n", + "Using our numerical methods we are left if some degree of error.\n", + "\n", + "<figure>\n", + "<img src=\"attachment:figures/truncationError.png\"\n", + "alt=\"Representation of truncation error under a curve\" />\n", + "<figcaption aria-hidden=\"true\">Representation of truncation error under\n", + "a curve</figcaption>\n", + "</figure>\n", + "\n", + "In order to reduce truncation error there are a few things we can do: -\n", + "Include more terms (higher-order methods) - Decrease step sizes (e.g.,\n", + "smaller $\\Delta x$ in approximations) - Use better approximation\n", + "algorithms.\n", + "\n", + "## Round-off Error\n", + "\n", + "Round-off error is caused by **the limited precision** with which\n", + "computers represent numbers. Since computers cannot store an infinite\n", + "number of digits, **they round off** after a certain number of decimal\n", + "or binary places. For example, instead of representing π with infinite\n", + "decimal places it may be rounded off to approximately 16 digits\n", + "depending on number of bits and the representation of the bits.\n", + "\n", + "In other words, round-off error happens because of how computers store\n", + "numbers. For a double-floating point, the number is stored using\n", + "64-bits. The more bits we use, the more precise of a number we can\n", + "store. However, it makes it costs us more memory making it more\n", + "computational expensive.\n", + "\n", + "While individual round-off errors may seem negligible, their effects can\n", + "**accumulate over repeated computations**, leading to significant\n", + "inaccuracies. This is particularly problematic in operations such as\n", + "**subtracting two nearly equal numbers**, where **loss of significance**\n", + "can occur, severely reducing numerical precision and amplifying the\n", + "impact of round-off error.\n", + "\n", + "### How to Reduce Round-off Error:\n", + "\n", + "To reduce round-off error, use higher-precision data types when storing\n", + "numerical values. Additionally, code and algorithms should be structured\n", + "to **avoid subtracting nearly equal numbers**, a common source of\n", + "significant error. Finally, employing **numerically stable algorithms**\n", + "is essential for minimizing the accumulation of round-off errors during\n", + "computation.\n", + "\n", + "## Total Error\n", + "\n", + "Truncation and round-off error are inversely proportional, meaning that\n", + "if we decrease one, the other increases. If we want to minimize total\n", + "error we must find the optimal point between step size and error.\n", + "\n", + "<figure>\n", + "<img src=\"attachment:figures/totalError.png\" alt=\"Total Error\" />\n", + "<figcaption aria-hidden=\"true\">Total Error</figcaption>\n", + "</figure>" + ], + "attachments": { + "figures/totalError.png": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAB7sAAAVkCAYAAACl+3u0AAAAOXRFWHRTb2Z0d2FyZQBNYXRwbG90\nbGliIHZlcnNpb24zLjYuMywgaHR0cHM6Ly9tYXRwbG90bGliLm9yZy/P9b71AAAACXBIWXMAAB7C\nAAAewgFu0HU+AAEAAElEQVR4nOzdd1yV9f//8SccFBQVcCHOnDhAzZUrtTTN0pZlpZmWK9PUHGn2\nceXKmamYM82ZszLNMs29Ek3NheLIAaLiRGSf3x/99Cueg8I5F+PA4367dbvF65zrdb0OXIfovK73\n6+1kNpvNAgAAAAAAAAAAAADAgTindwEAAAAAAAAAAAAAAKQUzW4AAAAAAAAAAAAAgMOh2Q0AAAAA\nAAAAAAAAcDg0uwEAAAAAAAAAAAAADodmNwAAAAAAAAAAAADA4dDsBgAAAAAAAAAAAAA4HJrdAAAA\nAAAAAAAAAACHQ7MbAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAABwOzW4AAAAAAAAAAAAAgMOh2Q0A\nAAAAAAAAAAAAcDg0uwEAAAAAAAAAAAAADodmNwAAAAAAAAAAAADA4dDsBgAAAAAAAAAAAAA4HJrd\nAAAAAAAAAAAAAACHQ7MbAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAABwOzW4AAAAAAAAAAAAAgMNx\nSe8CsoLmzZvrypUrKliwoNavX5/e5QAAAAAAAAAAAACAw6PZnQauXLmiy5cvp3cZAAAAAAAAAAAA\nAJBpMMYcAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAABwOzW4AAAAAAAAAAAAAgMOh2Q0AAAAAAAAA\nAAAAcDg0uwEAAAAAAAAAAAAADodmNwAAAAAAAAAAAADA4dDsBgAAAAAAAAAAAAA4HJrdAAAAAAAA\nAAAAAACHQ7MbAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAABwOzW4AAAAAAAAAAAAAgMOh2Q0AAAAA\nAAAAAAAAcDg0uwEAAAAAAAAAAAAADodmNwAAAAAAAAAAAADA4dDsBgAAAAAAAAAAAAA4HJrdAAAA\nAAAAAAAAAACHQ7MbAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAABwOzW4AAAAAAAAAAAAAgMOh2Q0A\nAAAAAAAAAAAAcDg0uwEAAAAAAAAAAAAADodmNwAAAAAAAAAAAADA4dDsBgAAAAAAAAAAAAA4HJrd\nAAAAAAAAAAAAAACHQ7MbAAAAAAAAAAAAAOBwaHYDAAAAAAAAAAAAAByOS3oXAAAAAAAAACDjSkhI\nUEREhO7cuaPY2FglJCQoPj4+vcsCAADAE5hMJjk7OytbtmzKnTu3cuXKJWfnzLUWmmY3AAAAAAAA\ngETMZrPu3LmjO3fuKCIiQgkJCeldEgAAAFIoLi5OknTv3j3dvn1bzs7OypUrl3Lnzq3cuXPLyckp\nnSu0H81uAAAAAAAAAA+YzWaFhobq1q1bVh93cnKSyWRK46oAAACQUvHx8TKbzQ++TkhI0O3bt3X7\n9m15eHjIx8fH4RveNLsBAAAAAAAASLLe6DaZTA9W/+TMmTPTjb4EAADIzBISEhQZGflgas/97Wju\n/73n6A1vmt0AAAAAAAAArDa6fXx85OHh4dAfgAIAAGRl90eX58qVS4UKFdKtW7cUGhoqKXM0vLkN\nEwAAAAAAAIDu3LmTqNFdpEgReXp6OuwHnwAAAEjMyclJnp6eKlKkyIPYrVu3dOfOnXSsyj40uwEA\nAAAAAAAk+pDTx8dHefLkScdqAAAAkFry5MkjHx+fB1/T7AYAAAAAAADgsBISEhQRESHpvz26PTw8\n0rkiAAAApCYPDw+ZTCZJUkREhBISEtK5ItvQ7AYAAAAAAACyuIc/4MydOzejywEAADI5Jycn5cqV\nS1LiGx8dDc1uAAAAAAAAIIt7eHRl7ty507ESAAAApJWHt62h2Q0AAAAAAADAIcXGxj7495w5c6Zj\nJQAAAEgrD//d9/Dfg46EZjcAAAAAAACQxd0fYe7k5CRnZz4yBAAAyAqcnZ0fbF8THx+fztXYhr9c\nAQAAAAAAgCzu/oebJpMpnSsBAABAWrr/9x/NbgAAAAAAAAAAAAAA0gjNbgAAAAAAAAAAAACAw6HZ\nDQAAAAAAAAAAAABwODS7AQAAAAAAAAAAAAAOh2Y3AAAAAAAAAAAAAMDh0OwGAAAAAAAAAAAAADgc\nmt0AAAAAAAAAAAAAAIdDsxsAAAAAAAAAAAAA4HBodgMAAAAAAAAAAAAAHA7NbgAAAAAAAAAAAACA\nw6HZDYcSEhKiVq1a6dSpU+ldCgAAAAAAAAAAmc4vv/yiGjVqJPpn2LBh6V0WAFhFsxsOpX///lq9\nerX8/Pz0xRdf6O7du+ldEgAAAAAAAAAAAIB04JLeBQDJtWXLFi1ZskSSFBMTo9GjR2vhwoWaPHmy\nXn/9dTk5OaVzhQAAAAAAAADSU0hIiF555ZX0LkOStGbNGhUuXDi9ywAAIFOj2Q2HEBsbqx49eljE\nL1y4oFatWqlp06aaOnWqypUrlw7VAQAAAAAAAACQtq5cuaLg4OBEsYIFC6pMmTLpVBEApD2a3XAI\n06ZN09GjR5N8fMOGDfLz81O/fv30xRdfyN3dPQ2rAwAAAAAAAAAgbe3du1fDhw9PFGvRogX7awPI\nUtizGxleaGiohg4d+sTnxcbGasyYMapQoYJWrVols9mcBtUBAAAAAAAAAAAASA+s7EaG179/f925\ncyfZz79w4YLefPNNvfDCC5o6dap8fX1TsToAAAAAAAAAGUX+/Pk1b948m4796quvFBQUlCjm6+ur\ngQMH2lwL4Ihatmypli1bpncZAJAsNLuRoW3dulWLFy+26dg//vhD/v7+6tOnj/73v/8pV65cBlcH\nAAAAAAAAICPJnj27/P39bTrW2taI7u7uNucDAACpjzHmyLBiY2PVo0cPu3OMHTtWFSpU0IoVKxht\nDgAAAAAAAAAAAGQSNLuRYf3xxx86cuSIIbkuXryo1q1bq2nTpjpx4oQhOQEAAAAAAAAAAACkH5rd\nyLBeeuklbdmyRX5+fobl3LhxoypXrqwBAwYoIiLCsLwAAAAAAAAAAAAA0hZ7diNDa9iwoQ4cOKCA\ngAANGTJEd+7csTtnbGysxo0bp8WLF2vSpEl666235OTkZEC1AAAAAAAAAPBkV69e1cmTJxUSEqK7\nd+8qPj5euXLlUqVKlQxd/JPerly5ouPHjys0NFR3796Vu7u7PD099dRTT8nX1zdNPpc9f/68zp49\nq7CwMEVGRio+Pl45c+ZU7ty5Vbx4cZUsWVK5c+c25FwJCQkKCQnRuXPndPXqVd29e1fR0dHKlSuX\nPDw8lDdvXlWsWFG5cuUy5HyOKCEhQWfOnNHZs2d15coV3bt3Ty4uLsqVK5d8fHxUvnx55cuXL83r\nunjxooKCghQWFqZ79+4pd+7c8vLyUtmyZfXUU0+leT22unHjhoKCghQaGqrbt28rPj5enp6eyps3\nr4oVK6bSpUuneU3nzp3T6dOndeXKFUVGRspkMilPnjyqU6eOfHx8bMqZkJCg4OBgnT17VteuXXtw\nHXl6eqpRo0by9PRMdq7Q0FCdOnVKoaGhioyMlNlsVs6cOeXt7a1SpUqpRIkSNtVoj5s3b+rEiRO6\ndOmS7ty5o7i4OLm7u6t06dKqVatWmteT0dHsRoaXLVs29e7dW2+//bY+++wzLVq0yJC8ly5d0ttv\nv61Zs2Zp6tSpqlChgiF5AQAAAAAAAGQtISEheuWVVxLFfHx89Msvvzz4+t69e/rxxx/1888/6/Tp\n01bztGjRwqLZPXPmTM2ePTtRrHPnzuratWuq1WrPsQkJCVq/fr2WLVumY8eOJZkrb968atasmTp2\n7JiixlRy7Nu3T2vXrtWOHTt069atJz6/TJkyql27tpo2baqKFSum6FxHjx7V7t27tX//fh0+fFjR\n0dGPfb6zs7PKli2r5557Tq1bt1aePHlSdL4aNWo89vG1a9dq7dq1ycoVGBhoNf7LL79o+PDhiWIt\nWrTQsGHDkpXXmiNHjmjlypXaunXrExe1lSpVSs2aNdObb74pDw8Pm84XGBiojz76KFGsWrVqmjVr\n1oOvo6Oj9dNPP2nVqlU6c+ZMkrkKFSqkli1bql27dsqZM6dN9aSm8PBw/fjjj/rjjz+S/N1yn7e3\nt+rVq6e2bdva3MRNzvVx+fJlLVu2TL/99puuXr1qNc/QoUPVsmXLB18n53fd2bNntXTpUm3atCnJ\n93bRokWf+D65fPmyVqxYoT/++EMhISGPfW6+fPnUuHFjtW7d2q4bH6zV9PB7MC4uTmvXrtVPP/2k\nY8eOKSEhweL51apVo9ltBc1uOAwfHx8tXLhQnTt3Vo8ePfTPP/8YknfTpk2qXLmyPv30Uw0ePNiw\nu/gAAAAAAAAAQJL27NmjESNGKCwsLL1LSVX//vuvBg8e/Ngm933Xr1/X0qVLtWbNGg0dOlTPP/+8\n3ec/ePCgJk2alKzzPyw4OFjBwcFatGiRfH19tXjx4iceM3fuXK1Zs0aXLl1K0bkSEhIUFBSkoKAg\nLVy4UO+//74+/PDDTDt9NCwsTGPHjtW2bduSfcyZM2f07bff6vvvv1eXLl3Upk0bOTsbuyvvkSNH\nNGTIEJ0/f/6Jz718+bJmz56t1atXa+zYsapataqhtdgqKipKc+bM0dKlS594k8V9YWFhWr16tX7+\n+We1atVKH3/8seGTBhYtWqRvv/022TUlR1xcnKZPn67FixcrPj7e5jxRUVGaOXOmli5dqri4uGQd\nEx4eruXLl2vlypV69dVX1bNnT8P7SMePH9eQIUN09uxZQ/NmFezZDYfToEEDHThwQJMnT07xXW9J\niYuL0/jx41W+fHktW7ZMZrPZkLwAAAAAAAAAsraffvpJvXr1yvSN7oMHD+qDDz5IcaP57t27+vzz\nz7Vu3Tqbz52QkKDp06erS5cuKT7/o4KCgpL1vFWrVqW40f2ou3fv6ttvv1Xfvn119+5du3JlRPv3\n71ebNm1S1Oh+WGRkpCZPnqzevXsrIiLCsLr+/PNPde3aNVmN7oeFh4ere/fu2rt3r2G12OrcuXNq\n166d5s+fb1NTOT4+XsuXL1enTp2SXHmdUmazWcOHD9fkyZMNbXTHxMTo008/1YIFC+xqdIeFhalj\nx45auHBhshvdD0tISNCPP/6odu3aGdqU3rlzpzp16kSj2w40u+GQXFxc1KtXLwUFBaldu3aG5Q0J\nCdE777yjJk2a2P1HEQAAAAAAAICsbefOnRozZoxFgyZPnjwqW7asatSooXLlytk8qjmjCA4OVu/e\nvXX79u1EcQ8PD5UrV041a9ZU+fLl5e7ubvX4+Ph4jR49WhcuXEjxuePj4zV48GB99913Vsf+3uft\n7a3y5curZs2aqlixoooUKWL4amFJMplMKlKkiMqXL68aNWqoWrVqKleunHLkyJHkMdu2bdPQoUMN\nryU97d+/Xz179kxy1LTJZFKxYsVUrVo1VaxY8bH7dO/atUs9e/ZUVFSU3XX99ddf+uKLLyyasfny\n5VOFChVUs2ZNlStXTq6urlaPj46O1pAhQ5I1Hj+1BAUFqWPHjo9tjnp7e6tixYoPXk9S773g4GB9\n+OGHunLlit11TZ8+3ep2CAUKFFCFChVUvXp1PfXUU499L1gzfPhw7d692yLu4+OjSpUqqVq1aipW\nrFiSPzNJunbtmrp27frYm1m8vb3l5+enqlWrqkiRIklOW7h48aK6du2qc+fOpeh1WBMUFKQBAwZY\nXI85c+ZUqVKlVL169XTbx96RMMYcDq1QoUJasGCBOnfurO7duxs22vzPP/9UlSpV1Lt3bw0ZMoTR\n5gAAAAAAAABSJDIyUl9++eWDRrezs7NefvllvfHGG6pUqZJFo/XQoUOGrbBMSzExMRowYMCDlbcu\nLi567bXX9Nprr8nX1zdRwyguLk579uxRQECATp06lShPdHS0vvrqKwUEBKTo/BMmTNDvv/9u9bFS\npUqpTZs2qlu3rgoWLGjxeGRkpI4fP67t27frjz/+sGn1ffbs2VW9enU1aNBA/v7+KlWqlLJnz27x\nvISEBJ0+fVrr16/XqlWrLFZyb9myRcuWLdPbb7/92PPNmzfvwb/v2LFDc+fOTfR4vXr11KlTpxS/\nDiPdvHlTgwYNsrq6N1++fOrcubOaNGlisVf7iRMntHr1av34448W01cPHz6sr7/+Wp9//rnNdd24\ncUNffPGFYmNjJUlubm5699139dJLL6lkyZKJnhsVFaWtW7cqICDAYk/n8PBwTZs2TV988YXNtdjq\n1q1b6tOnj9Vme9GiRdW2bVs1aNBA3t7eiR6Li4vTgQMHNG/ePO3bty/RY6GhoRo6dKimT59u8zj9\no0eP6t9//33wtbu7u9577z01a9ZMxYsXt6hl27ZtKlCgwBPzbtq0KdF+6nnz5tUHH3yg559/3uI1\nRkVFaePGjcqfP3+iuNls1tChQ3Xx4kWL/NmzZ1fbtm3VsmVLizrDwsK0fv16zZs3z+L9ev36dQ0a\nNEjff/+9smXL9sTXkZTBgwcnuomjYcOGevfdd1W1alW5uCRu4QYHB+vo0aM2nyszo9mNTOHZZ5/V\ngQMHNH36dA0ePNjiDkJbxMXFacKECVqyZIkmTpyot99+O9PumwIAAAAAAADAWA83ozw9PTV58mT5\n+fkl+fwqVaqkRVmGCw8PV3h4uKT/FidNnjxZZcqUsfpcFxcX1a9fXzVq1FDfvn0txkHv3btX//77\nr0qUKJGsc2/cuFErVqywiJtMJvXp00dvvvmmTCZTksfnzJlT1atXV/Xq1dWrVy9t3bpV3333XbLO\nXahQIb3zzjt64403krXnsbOzs8qWLauyZcuqTZs2Gjx4sEXTcdasWXr11Vfl5uaWZB5/f/8H/25t\nZamXl1ei56SHkSNHPrgmHlavXj2NGDEiye1Jy5cvr0GDBqlZs2bq37+/xef8q1atUv369fXss8/a\nVNfDK6HLlSunSZMmqVChQlaf6+bmpmbNmumZZ57Rxx9/rJMnTyZ6/Ndff1WvXr0M3+/6SYYNG2Zx\nU4aTk5Pef/99devWzaJBep+Li4tq1aqlWrVqaeXKlRo/fnyiiRP79u3T4sWL9d5779lU18Pf24oV\nK2rSpEkWTeeHa3n++eeTlffhRnf9+vU1cuTIJL/nbm5uatGihUV86dKlVkfPFy1aVJMmTVKpUqWs\n5vP29laHDh3UrFkz9evXz2JV+MmTJxUQEKDevXsn67VYc//1ubq6asyYMWrQoEGSzy1TpkySv1uz\nOprdyDRcXFzUs2dPtW7dWgMGDNCCBQsMyRsSEqJ3331Xs2bN0tSpU1WpUiVD8gIAAAAAAGRGUVHS\n6dPpXQVSS+nS0mP6cLAiR44cmjVrVpINlcwiX758+u6776yuoH6Um5ubRo0apVatWlmsUF27dq26\nd+/+xBz37t3T+PHjLeKurq4aO3as6tevn/zi9V/DsFGjRmrUqFGynj937lybF0flz59fX3/9tbp1\n65ZoWumtW7e0fv16vf766zblzQgCAwO1ZcsWi3j16tU1bty4x46afvi5kydP1scff2wxunzSpEmq\nX7++XQvTSpYsqdmzZyc52vthnp6eGj16tN59990HK8Kl/yYRbNiwQW+88YbNdaTU+vXrtX37dot4\n//791bp162TnefPNN+Xs7KzRo0cnis+fP19vvfVWsn5GSSlbtqy+/fbbZH1vU6J27dqaMGFCks38\npERERGjmzJkW8fz58ysgIEBFihR5Yg4fHx9NmzZNHTt2tNjnfcmSJWrdurUKFy6coroe5uzsrMmT\nJ6tmzZo258jqaHYj0ylUqJC+//77B6PNDx8+bEjezZs3q2rVqurVq5eGDh3KaHMAAAAAAAArTp+W\nHrN4FQ7uyBGJtSAp071790zf6JakIUOGJKvRfZ+np6datWplsZL60KFDyTp++fLlVlcP9+jRI8WN\nblvYOwXUzc1NgwYN0rvvvpso7ujN7mXLllnEcuTIoS+//DJFTdTKlSurc+fOmjp1aqL4hQsXtHPn\nTpt/xiaTSWPGjElRM/app55SkyZNtH79+kTxQ4cOpWmz29oCv1dffTVFje773njjDe3cuVNbt259\nELt586bWr1+v1157zab6TCaThg4danij293dXYMHD05xo1v67+aZR0eQS9LAgQOT1ei+z8vLS8OH\nD9eHH36YaMR+QkKCVqxYoV69eqW4tvveeecdGt12cn7yUwDHVL9+fe3fv19TpkyRh4eHITnj4uI0\nceJE+fr6aunSpRb7hgAAAAAAAADAffny5dObb76Z3mWkOn9/f9WrVy/Fx73wwgsWsaCgoCd+7mo2\nm7V69WqLeOXKlfXOO++kuI70UrZsWfn6+iaKHTt2LNF4aUcSFhambdu2WcTbt29vsb9ycrRt21ZF\nixa1iC9fvtym+iSpcePGNo2CbtKkiUXs+PHjNteRUrt377bY597d3T1ZUxCS0rlzZ4vYmjVrbM7X\nsGFDlS9f3ubjk/L666/bdP1I1q+VmjVrJnuCw8P8/f3VvHlzi/jPP/9sdX/65MiePbs+/PBDm47F\n/6HZjUzNxcVFn3zyiYKCgtS+fXvD8oaGhqpNmzZ67rnndPToUcPyAgAAAAAAAMg8Xn75ZZtWIzqa\nV1991abjSpUqZbHa9+7du1ZXbD/s+PHjunTpkkW8TZs2dq+4TmsVK1ZM9HVUVJRFU9NR/PXXXxaN\nemdnZ5uvDxcXF73yyisW8cDAwEQjxVPC1loqVKhgEbtw4YJNuWyxYcMGi1jTpk2VN29em3OWL1/e\nYurE8ePHbW7c2vq9Ta28ISEhFmPHJdk1OaFVq1YWsdu3b9vcJ2rYsKE8PT1trgf/odmNLMHb21vz\n58/Xjh07VLVqVcPybt26VVWqVFHfvn11+/Ztw/ICAAAAAAAAcHw1atRI7xLShK2fuZpMJvn4+FjE\nIyIiHnvc3r17LWIeHh42rdZMb9aalRcvXkyHSuxnbUvRp59+WgUKFLA5p7WVtDExMQoKCkpxLpPJ\npMqVK9tUR8GCBS1uzIiNjbW5MZxSBw4csIg9//zzdud99L0bGxtr04p1Z2dnVatWze56HpUvXz6V\nLFnSpmOtXY+urq5q0KCBzfVUqVLF6v7ctm6nW716dZtrwf/J/LeUAQ+pV6+e9u3bpxkzZuh///uf\nbt26ZXfO+Ph4TZo0SUuXLtX48eMd8u5BAAAAAAAAAMaztho0szGZTCpRooTNx1vb3/dJzW5rzTh/\nf/90XUUfExOjvXv36tixYzp16pTOnz+viIgI3b17V5GRkSnaEvNJrz+jOnLkiEXMz8/Prpw+Pj7K\nly+fxWr/w4cPpzh3oUKFlCNHDptrcXd3t2huR0REpGgvcltcuXLF6iQDI36/WGvcnjp1KsU3sDz1\n1FN2fW+TYs9YdGvXY9myZeXm5mZPSfLz81NISEii2D///GNTrqzw34i0QLMbWY6Li4t69Oih1q1b\na8CAAZo/f74heUNDQ/Xee+9p1qxZCggIsPs/4gAAAAAAAAAcV7Zs2eTl5ZXeZaS63Llz27X4x1qj\n8EmrZa2Nj06vz2MvX76suXPnauPGjbpz544hOY3Kk9ZCQ0MtYo/uSW4LX19f7dq1K1Hs8uXLKc7j\n4eFhVx3WrtWYmBi7cibH6dOnLWI5c+bUhQsX7B6lbu1as2WRYMGCBe2qIzXypub1+OhYeVuuR0k2\n70WOxGh2I8sqWLCg5s2bp86dO6t79+46ePCgIXm3bdumqlWrqmfPnho2bJjy5MljSF4AAAAAAAAA\njiNXrlzpXUKaSI3VnE9aBX3lyhWLWGo12x7n+++/1+zZsxUVFWVo3nv37hmaLy0kJCTo7t27FvH8\n+fPbndvaGHRbbgiwd0WvNSlZsW8ra83nyMhIffDBB6lyPlu2bE2t33f25LV2jWSk61HKOv+dSG3s\n2Y0sr27dugoMDNS0adPk6elpSM74+Hh9/fXX8vX11aJFi9LkP3gAAAAAAAAAMo7UaKzhP9aawblz\n507TGsaPH6+pU6ca3uiW0qaBarQ7d+5YrdvamPqUstYQtKUh66iM2I41JWwZo59av+/syWvtGslo\n1yP/nTAGK7sB/bevTPfu3fXWW2/p888/13fffWdI3suXL6tdu3YPRpv7+/sbkhcAAAAAACCjKl1a\nsrJNJjKJ0qXTuwLgv8VGj0rtfZMf9sMPP2jZsmVWH3NxcZGvr6/8/Pzk4+Mjb29v5cyZU66ursqe\nPbvFyPeffvpJP//8c1qUnaqSGj1vxM/FWg5HXP1uq7Qea5+QkJCm50st1q5JrsfMiWY38JCCBQtq\n7ty56tSpk7p3766///7bkLzbt2/X008/rU8++UTDhg2ze28QAAAAAACAjMrNTapUKb2rAJCZ5c6d\nWzdv3kwUszZCOzVcv35dM2bMsIi7urqqU6dOeuONN1L0+e/27duNLC/dJLViNjIy0u7c1nJkpfHP\nLi608mxh7ZrkesyceIcAVtSpU0f79u3TzJkz9cUXX1j84WSL+Ph4TZ48WUuXLtX48eP13nvvWdzF\nBwAAAAAAAACpKS4uLr1LsFuePHksPrNNq9Wvv/76q8WYZzc3N82ZM0fly5dPcb60XrWbWtzd3WUy\nmSxW3RtxE4K1sdpZaUGZtaZt3rx5tWHDhnSoxnHkyZPHIsb1mDmxZzeQBJPJpI8//lgnT55Ux44d\nDcsbFham999/Xw0aNNDhw4cNywsAAAAAAAAg8zGZTBYxa2O8kyut9/9NDZ6enhaxCxcupMm5t23b\nZhHr1KmTTY1uSYYstMoorO2bfunSJbvzXrx4MVnnyqy8vb0tYpnhfZzauB6zDprdwBMUKFBAc+bM\n0e7du1WtWjXD8u7YsUPVqlVTr169+A8TAAAAAAAAAKusreq0Z3/YK1eu2FNOhuDr62sR++eff9Lk\n3MePH7eIvfTSSzbnO3HihD3lZCilSpWyiAUFBdmV02w269SpU8k6V2Zl7bXGx8dnivdyakqN6zGp\nHFnpesyIaHYDyVS7dm399ddfmj59ury8vAzJGR8frylTpsjX11cLFiyQ2Ww2JC8AAAAAAACAzMHa\nXrDXrl2zOd+hQ4fsKSdDsLYo6fjx46k+EvzevXsWNxq4u7urYMGCNuW7du2aXSvSM9o2mf7+/hax\n/fv325Xz2LFjVkdPWztXZlW0aFGrPYnAwMB0qMZxWLtGzp07p/DwcJtzxsbGWp3Ym5Wux4yIZjeQ\nAiaTSd26ddPJkyfVqVMnw/KGhYWpffv2evbZZzPFH5sAAAAAAAAAjFGgQAGLWHBwsE25zGazduzY\nYW9J6c5aszs6Olpr1qxJ1fNa26s3R44cNuf7+eef7SlH2bJls4il557slStXtoidOXPGrtW069at\ns4h5eHioRIkSNud0RPXr17eIbd68OR0qcRz+/v4WN4QkJCTo999/tznntm3bdPv2bYu4tWsfaYdm\nN2CD/Pnza/bs2dqzZ4+qV69uWN6dO3eqWrVq6tmzZ6baqwUAAAAAAACAbaztBX3u3Dldvnw5xbm2\nbt2q8+fPG1FWusqXL5/q1q1rEV+6dKnVVcBGsbbK/ubNm4qNjU1xrnv37mnVqlV21WP0iHt71apV\ny+rexUuWLLEp340bN7R+/XqLeOPGjW3K58hefvlli9iWLVusjnjHf3Lnzq1atWpZxFeuXGnTe9Zs\nNlu9lkuWLKnSpUvbVCOMQbMbsMMzzzyjvXv3asaMGYaNNk9ISNDUqVPl6+ur77//XgkJCYbkBQAA\nAAAAAOB4PD095ePjkyhmNptTvCr49u3bmjBhgpGlpav27dtbxC5fvpyqrzFHjhwWDea4uDj99ddf\nKc41adIku/dcttZYDg0NtSunPXLkyKFXXnnFIv7rr7/aNNF0ypQpVkfTv/322zbV58hq1KhhceOL\n2WzWsGHD0vUGh4zO2rVy/vx5LV68OMW51q1bZ/U6bt26dYbbUiCrodkN2MlkMqlr1646efKkOnfu\nbNgvtStXrqhDhw569tlndfDgQUNyAgAAAAAAAHA81layLly4UP/++2+yjo+IiNBnn31m02rwjKp6\n9ep6+umnLeK//PKLpkyZYnPeq1evPvZxa+ecOXNmisaHL1q0SD/++GOKa3tUqVKlLGJnzpyxOm49\nrbz11ltycXFJFDObzfr8888VEhKS7Dw//PCDfvnlF4t47dq1s+wq2k8//dSi/xAUFKT+/fsbsl/9\n/v37tXfvXrvzZCT169dX8eLFLeIzZsxI0ZYOhw8f1tixYy3iHh4eVlfdI23R7AYMkj9/fs2aNUt7\n9uxRjRo1DMu7a9cuVa9eXZ988gmjzQEAAAAAAIAs6NVXX7WIRUVF6eOPP9axY8cee+z+/fvVsWNH\nBQYGSpLc3NxSpcb0MHz4cOXJk8civmDBAvXt21cXLlxIdq7Tp09rzJgxVr/XD2vUqJFF7NixYxo0\naJAiIyMfe2xERITGjh2ryZMnP4iZTKZk1/io3Llzq0iRIolicXFxmj9/vs057VW0aFF16dLFIn7l\nyhV99NFHOnDgwGOPj42N1YwZMzRx4kSLx3LmzKmBAwcaVqujqV69ut555x2L+J49e9SmTRtt3bpV\nZrM5RTmvXr2qlStXqm3bturatauOHz9uVLkZgrOzs4YMGSJn58Tt0Li4OA0YMECrV69+4vdsw4YN\n6tWrl9UV9AMHDlTOnDkNrRkp5/LkpwBIiVq1amnPnj2aO3euPv/8c12/ft3unAkJCZo2bZqWLVum\ncePG6f3337f45QwAAAAAAAAgcypZsqRefvllrVu3LlE8LCzswXTIevXqqXDhwsqWLZtu3Lihs2fP\naseOHTp69OiD5zs7O6tfv34aOXJkWr+EVFG4cGENHTpU/fr1s2hYbd26VTt37lTDhg1Vr149+fv7\ny8vLS7ly5VJkZKRu3ryp4OBgHTt2TNu2bdOZM2eSdc6XX35Zc+fOtRgX/ueff+ro0aN66623VLt2\nbRUtWlRubm66ceOGLly4oO3bt2vdunWJPi/28vLS888/b9fe3Y0bN9aCBQsSxebPn6/Dhw/rueee\nU/HixeXu7m61qe7v72/zeR+nQ4cO2rVrl8XE0pCQEHXt2lWNGjVSs2bNVKFCBeXLl08xMTEKCwvT\nzp07tWbNmiT3le/bt6+KFi2aKjU7il69eunff//Vrl27EsVDQ0PVt29fFStWTE2aNFGVKlVUsmRJ\neXh4KEeOHLp3754iIiJ048YNnT59WqdOndLBgwd17NixFDfIHU3VqlXVvn17zZs3L1E8Ojpao0eP\n1k8//aQWLVqoVq1ayp8/v0wmk65evaqDBw9q3bp12r9/v9W8L730kl544YW0eAl4AprdQCowmUzq\n0qWLWrVqpUGDBmn27NmG/Afj6tWr+uCDDzRr1iwFBARYHZkDAAAAAAAAIPPp27ev9u3bZ7HPc0JC\ngrZu3aqtW7c+Mcdnn32mWrVqpVaJ6aJhw4b64osvNHr0aCUkJCR6LC4uTps2bdKmTZsMO1+2bNk0\naNAg9e7dW/Hx8YkeCwsL07Rp0zRt2rQn5smePbvGjBmTZCMtud544w0tW7ZM0dHRieIHDhx44irq\n+6v9jebs7KyxY8eqa9euOnfuXKLHzGazNm/erM2bN6coZ7t27Z646j4rcHFx0bhx4/TFF19Yfc9f\nuHDBoqkL6aOPPtL58+et/i44duzYEydkPKpatWoaNGiQUeXBTiwNBVJRvnz5NHPmTO3du1c1a9Y0\nLO/u3btVo0YN9ejRQzdu3DAsLwAAAAAAAICMKU+ePJo5c6Z8fHxSfGy2bNk0ZMgQvfnmm6lQWfp7\n7bXXNGXKFOXLly9NzlenTh0NGDDA5hHk7u7uGjdunCHbYRYtWlR9+vSxO4/R8uXLpzlz5tj9ubjJ\nZNKnn36qXr16GVSZ43Nzc9P48ePVo0cPZcuWzdDcj+63nlmYTCaNGjVK7777rt25mjdvrilTpmSq\nLSEcHc1uIA3UrFlTe/bs0axZs5Q3b15DciYkJCggIEC+vr6aN2+exV2LAAAAAAAAADKXYsWKad68\neWrZsmWytzl8+umntXDhQr3yyiupXF36ql27tlauXKk2bdooR44cNuUoWrSoevTokaznvvHGG5o2\nbZq8vb1TdI7q1avr+++/V/369W0p0apWrVppwoQJKliwoGE5jeDp6amAgAANHDjQphsRatSooYUL\nF6pt27apUJ1jc3Z2VocOHbRixQo1b97crqZ3rly51LJlS82YMSNTf69dXFzUt29fffvttypXrlyK\njy9evLjGjRunESNG0OjOYJzMmX0YfwZQvXp1Xb58WYUKFbJ7JAkcX3h4uL744gvNmjXL0L0wateu\nrYCAAFWrVs2wnAAAAAAAIGs4deqU4uLi5OLiorJly6Z3OUC6OHPmjO7evZso5u7urlKlSqVTRY93\n7tw5bdmyRXv37lVISIhu3LihmJgY5cqVS8WLF1eVKlXUuHFj+fn5pXepae7OnTvauHGjduzYoX/+\n+SfRPtkP8/DwUOnSpVW9enXVrVtXfn5+cnJyStG5YmNj9euvv2rjxo06ePCg7t27l+hxJycnFSlS\nRM8884xeeuklValSJdHjR44cSbSvuiRVqlTJpp9bfHy8du/erb179+rkyZO6dOmS7t69q8jISIuR\n61LqjTG3JiYmRn/++ac2b96sgwcPKjw83OI5JpNJpUqVUs2aNdW8eXNVqFAhzepzdNevX9eff/6p\n3bt36/jx4xbbHdxnMplUuHBhPfXUU/Lz81OtWrVUsWJFm6cUOLLAwEBt2LBBgYGBunDhgtV+TeHC\nhfX000/rhRdeUN26dZN9k5GjcfS/A2l2pwGa3bAmMDBQ3bt3119//WVYTicnJ3Xr1k0jR46Ul5eX\nYXkBAAAAAEDm5ugfcgLA40REROjatWu6d++enJyc5O7uLg8PD+XJk8fQ88TFxen69eu6deuW4uPj\nlSNHDnl7e7MK1IqIiAhduXJFUVFRcnZ2Vq5cuVSoUKFMO0Y7rUVFRenKlSuKjIxUQkKCcubMKXd3\nd3l6eho++jwziI6OVlhY2IMbnu6/d22dEuFoHP3vQJrdaYBmN5KSkJCg7777TgMHDrR6J5ut8ufP\nr7Fjx6pDhw6Z9k4jAAAAAABgHEf/kBMAAAC2cfS/A+mCAenI2dlZnTp10smTJ/XRRx+leEROUq5d\nu6aOHTuqbt263GABAAAAAAAAAACATIlmN5AB5M2bV99++6327dunZ555xrC8e/fuVc2aNdWtW7ck\n96UBAAAAAAAAAAAAHBHNbiADqV69unbt2qU5c+Yof/78huQ0m82aMWOGypUrpzlz5ighIcGQvAAA\nAAAAAAAAAEB6otkNZDDOzs7q2LGjgoKC9PHHHxs22jw8PFydO3dWnTp1FBgYaEhOAAAAAAAAAAAA\nIL3Q7AYyqLx58yogIECBgYGqXbu2YXn/+usv1apVSx999JHCw8MNywsAAAAAAAAAAACkJZrdQAZX\nrVo17dy5U999952ho81nzpwpX19fzZ49m9HmAAAAAAAAAAAAcDg0uwEH4OzsrA8++EAnT55U9+7d\n5exszFs3PDxcXbp0Ue3atbVv3z5DcgIAAAAAAAAAAABpgWY34EC8vLw0bdo0BQYGqk6dOobl3bdv\nn5555hl17dqV0eYAAAAAAAAAAABwCDS7AQf09NNPa8eOHZo3b54KFChgSE6z2axZs2apXLlymjVr\nluLj4w3JCwAAAAAAAAAAAKQGmt2Ag3J2dlaHDh0UFBSkHj16GDba/Pr16+ratSujzQEAAAAAAAAA\nAJCh0ewGHJyXl5emTp2q/fv3q27duoblDQwM1DPPPKMuXbro2rVrhuUFAAAAAAAAAAAAjECzG8gk\nqlatqu3bt2v+/PmGjjafPXu2fH19NXPmTEabAwAAAAAAAAAAIMOg2Q1kIs7Ozmrfvr1OnjypTz75\nxNDR5h999JGeeeYZ/fXXX4bkBAAAAAAAAAAAAOxBsxvIhDw9PTVlyhQdOHBA9erVMyzv/v37Vbt2\nbXXu3JnR5gAAAAAAAAAAAEhXNLuBTKxKlSravn27vv/+exUsWNCQnGazWXPmzFG5cuU0Y8YMRpsD\nAAAAAAAAAAAgXdDsBjI5Jycnvf/++woKClLPnj0NG21+48YNdevWTbVq1dLevXsNyQkAAAAAAAAA\nAAAkF81uIIvw9PTUN998owMHDqh+/fqG5T1w4IBq166tTp066erVq4blBQAAAAAAAAAAAB6HZjeQ\nxVSpUkXbtm3TggUL5O3tbVjeuXPnqly5cpo+fTqjzQEAAAAAAAAAAJDqaHYDWZCTk5PatWunoKAg\n9erVSyaTyZC8N2/eVPfu3VWrVi3t2bPHkJwAAAAAAAAAAACANTS7gSzMw8NDkydP1oEDB/Tss88a\nlvfAgQOqU6eOPvzwQ125csWwvAAAAAAAAAAAAMB9NLsBqHLlytq6dasWLVqkQoUKGZZ33rx58vX1\nVUBAAKPNAQAAAAAAAAAAYCia3QAk/TfavG3btgoKCtKnn35q6GjzHj16qGbNmtq9e7chOQEAAAAA\nAAAAAACa3QASyZMnjyZNmqS///5bDRo0MCzv33//rbp16+qDDz5gtDkAAAAAAAAAAADsRrMbgFX+\n/v7asmWLFi9ebOho8/nz56tcuXKaNm2a4uLiDMsLAAAAAAAAAACArIVmN4AkOTk5qU2bNgoKClKf\nPn0MG21+69YtffLJJ6pRo4Z27txpSE4AAAAAAAAAAABkLTS7ATxRnjx5NHHiRB08eFANGzY0LO+h\nQ4dUv359dejQQWFhYYblBQAAAAAAAAAAQOZHsxtAsvn5+Wnz5s1asmSJfHx8DMv7/fffy9fXV1On\nTmW0OQAAAAAAAAAAAJKFZjeAFHFyctK7776rEydOqG/fvoaONu/Zs6eqV6+uHTt2GJITAAAAAAAA\nAAAAmRfNbgA2yZMnjyZMmKBDhw6pUaNGhuU9fPiwnn32WbVv357R5gAAAAAAAAAAAEgSzW4AdqlU\nqZL+/PNPLV26VIULFzYs74IFC1SuXDlNmTKF0eYAAAAAAAAAAACwQLMbgN2cnJz0zjvv6MSJE+rX\nr59cXFwMyXv79m316tVL1atX1/bt2w3JCQAAAAAAAAAAgMyBZjcAw+TOnVvjx4/XoUOH9NxzzxmW\n9/Dhw2rQoIHef/99Xb582bC8AAAAAAAAAAAAcFw0uwEYrmLFitq0aZN++OEHQ0ebL1y4UL6+vpo8\neTKjzQEAAAAAAAAAALI4mt0AUoWTk5PefvttnThxQv379zd0tPmnn36qatWqadu2bYbkBAAAAAAA\nAAAAgOOh2Q0gVeXOnVvjxo3T4cOH9fzzzxuW959//lHDhg3Vrl07hYaGGpYXAAAAAAAAAAAAjoFm\nN4A0UaFCBW3cuFHLli1TkSJFDMu7aNEi+fr66uuvv1ZsbKxheQEAAAAAAAAAAJCx0ewGkGacnJzU\nunVrnThxQgMGDDBstPmdO3fUp08fRpsDAAAAAAAAAABkIcZ0mgAgBXLlyqWvvvpKHTp00CeffKKN\nGzcakvfIkSNq2LCh2rZtq/Hjx8vHx8eQvAAAAAAAAABgi2HDhmnt2rWJYkOHDlXLli3TqaKMy2w2\na8+ePdq1a5eOHDmisLAw3blzR/fu3Uv0vFy5cmnLli1PzHft2jX99ttv+ueff3Tq1CndunVLERER\nio+PT/S8Pn36qE2bNka+FABpiGY3gHRTvnx5bdiwQStXrlSfPn108eJFQ/IuXrxYa9as0bBhw/TJ\nJ58oW7ZshuQFAAAAAAAAABjv77//1siRI/Xvv//anSs6OlrffPONfvzxR7a+BLIAmt0A0pWTk5Pe\neustNW/eXKNGjdLEiRMN+QPkzp076tu3r7777jtNmzZNjRo1sr9YAAAAAAAAOJyZM2dq9uzZKTrG\n1dVVuXLlkru7u7y9veXr66vy5curdu3a8vT0TJ1CgSzqt99+09ChQy1WXNsiKipKXbp00bFjxwyo\nDIAjYM9uABlCrly5NGbMGP3zzz964YUXDMt79OhRPffcc2rTpo1CQkIMywsAAAAAAIDMKzo6WuHh\n4Tp//rz27dunRYsW6X//+5+aN2+uAQMG6J9//knvEoFM4ezZsxoxYoQhjW5J+uqrr2h0A1kMK7sB\nZCi+vr76/ffftWrVKvXp00cXLlwwJO/SpUv1yy+/aNiwYerZsyejzQEAAAAAAJBisbGx2rRpkzZv\n3qzWrVurR48ecnNzS++yAIf13XffKTo6OlHM2dlZjRs3Vr169eTt7W3xHjOZTFZz/fvvv1q3bp1F\nvEiRImrZsqV8fX2VO3dui+N9fHzsfBUA0hPNbgAZjpOTk958880Ho80nTJhgyGjziIgI9evX78Fo\n8+eee86AagEAAAAAAJDVJCQk6IcfftCZM2c0efJkZc+ePb1LAhxORESE/vjjD4v46NGj1aRJkxTn\n+/nnn2U2mxPFKlWqpBkzZihHjhw21wkgY6PZDSDDcnd31+jRo9W+fXv17NlTGzZsMCTvsWPH9Pzz\nz+udd97RhAkTVKRIEUPyAgAAAAAAwHHMmzcvyceioqJ0+/ZtnT59Wvv379f+/futPu+vv/7SiBEj\nNGLEiNQqE8i0jhw5ori4uESxypUr29TolqSDBw9axLp160ajG8jkaHYDyPB8fX3122+/6ccff1Tv\n3r0NG23+ww8/aO3atRo6dKh69erFaHMAAAAAAIAsxN/f/4nPady4sSTpzJkzGjFihNW9utevX69W\nrVqpatWqRpcIZGonTpywiFWvXt3mfEFBQYm+NplMevrpp23OB8AxOKd3AQCQHE5OTnrjjTd0/Phx\nDRo0yLDRUBEREerfv7+qVKmiP//805CcAAAAAAAAyFxKlSql2bNnq1atWlYfnzVrVhpXBDi+W7du\nWcS8vb1tynXv3j2Lvb89PDzk6upqUz4AjoNmNwCH4u7urlGjRumff/5Rs2bNDMt7/PhxNW7cWO+8\n844uXbpkWF4AAAAAAABkDi4uLhoxYoTc3NwsHtu/f78iIiLSoSrAcVl7z9janDYyFwDHQrMbgEMq\nV66c1q9fr9WrV6t48eKG5V22bJl8fX01fvx4xcTEGJYXAAAAAAAAji9fvnx66aWXLOLx8fEKDAxM\nh4oAxxUbG5shcwFwLOzZDcBhOTk56fXXX1ezZs00evRowxrUd+/e1WeffabvvvtO06ZNe7A3EwAA\nAAAAAFCrVi2tXr3aIn7+/HlD8oeGhurUqVMKDQ1VZGSkzGazcubMKW9vb5UqVUolSpQw5DyOKiIi\nQseOHdP58+d1584dZcuWTZ6enipUqJAqV65s2PaH1ty4cUNHjhzRxYsXdffuXbm6usrLy0slS5aU\nr6+vXFwcv+USGRmp48eP6+LFi7p165ZiYmIevM7ixYvL19eXFdMGiY+PV3BwsM6fP6+rV6/q3r17\ncnNzU968eZUvXz5VrFhRuXLlStOaIiIidOLECV28eFG3b99WTEyMcuTIoSJFiqhRo0Y2571586ZO\nnDihS5cu6c6dO4qLi5O7u7tKly6d5PYQ1kRHRysoKEjnz5/XjRs3FB0drezZs8vDw0PFihVT+fLl\nlTNnTpvrtEVCQoKCg4N19uxZXbt2Tffu3ZOLi4s8PT3VqFEjeXp6pmk9WZHj/+YFkOXlzJlTI0eO\nVPv27dWzZ0/99ttvhuQ9ceKEmjRpotatW2vixIkqWrSoIXkBAAAAAADguIoUKWI1fuPGDZtzXr58\nWStWrNAff/yhkJCQxz43X758aty4sVq3bq2nnnrKpvMFBgbqo48+ShSrVq2aXXuPt2zZUqGhoYli\na9asUeHChQ059sCBA1q4cKH27NmT5CreHDlyqE6dOurSpYvKlCljw6uwbsuWLVqyZIn+/vtvmc1m\nq8/JkyePmjVrpvfeey/JaySjio2N1a+//qp169bp0KFDio+PT/K52bJlU61atfTqq6/queeek5OT\nU7LO8csvv2j48OFPfN7w4cMf+7wWLVpo2LBhVq+ZR4WGhqpGjRqPfU5yr1Ej7dixQ+vWrdPOnTsV\nGRmZ5PNcXFz09NNPq2nTpmrZsqXNN1M86f1lNpu1adMmrVq1SgcOHLD68/fx8bFodlv73j484SIu\nLk5r167VTz/9pGPHjikhIcHi+dWqVXtiszshIUF//vmn1qxZo3379j12Fb/JZFKVKlXUsmVLNW/e\n3Obv2cyZMzV79uxEsc6dO6tr164Pvj579qyWLl2qTZs2Wd1/XpKKFi36xGsQ9qPZDSDTKFu2rH79\n9Vf9/PPP6t27t/79919D8i5fvlzr1q3TkCFD1Lt371S9OxQAAAAAAAAZm7u7u9X4nTt3UpwrKipK\nM2fO1NKlSxUXF5esY8LDw7V8+XKtXLlSr776qnr27KncuXOn+NyO4u7du/rqq6+0fv36Jz733r17\n+vPPP7V161a9//776t69u13nvnbtmoYOHaq9e/c+8bm3b9/WihUrtGbNGvXo0UPvvvuuXedOK9u3\nb9fYsWN1+fLlZD0/NjZWO3fu1M6dO1W2bFl98cUX8vPzS+UqM4eDBw9q3LhxOnnyZLKeHxcXp337\n9mnfvn1asmSJ+vTpozp16hha08WLFzV48GD9888/huY9fvy4hgwZorNnz9qV59ChQxo9erROnz6d\nrOfHx8frwIEDOnDggGbPnq0BAwaoXr16dtXwqLi4OE2fPl2LFy9+7I0hSDvs2Q0gU3FyctJrr72m\nY8eOafDgwYY1pu/evasBAwaoSpUq2rhxoyE5AQAAAAAA4HgiIiKsxt3c3FKUJywsTB07dtTChQuT\n3eh+WEJCgn788Ue1a9fO7oZSRhUeHq6OHTsmq9H9sPj4eM2bN0+jRo2y+dznzp1T+/btk9Xoflh0\ndLQmTpyo8ePH23zutGA2m/XNN9/o008/TXaj+1GnTp1Sx44dtWLFCoOry1zMZrNmzZqlLl26JLvR\n/aizZ8+qZ8+e+uGHHwyr6/jx42rfvr3hje6dO3eqU6dOdv9eWrp0qbp06ZLsRvejQkJC1KtXLwUE\nBNhVx8NiYmL06aefasGCBTS6MxBWdgPIlHLmzKkvv/xS77//vnr27JniP4iTcuLECb3wwgt66623\nNHHiRBUrVsyQvAAAAAAAAHAMFy9etBrPmzdvsnNcu3ZNXbt2TTKXJHl7e6tAgQJycXHR1atXFRIS\nYnWE9sWLF9W1a1fNmjXL5rHmGVFkZKT69eun4ODgRHE3NzcVLlxYXl5eiomJUWhoqK5du2Y1x48/\n/qhq1aqpefPmKTr31atX1b17d4WFhVl93GQyycfHRwUKFFBMTIzCwsIsali2bJl8fHxSdN60NG7c\nuMc2qXPlyiUfHx95eHjo+vXrCg0N1b179yyeFx8fr7Fjxyo2NlZt2rRJzZIdktls1qhRo/TTTz8l\n+Zz717Snp6fi4uIUHh6uS5cuWc01YcIE3b17Vx07drSrritXruizzz6zGL/t6uoqHx8f5c2bV1FR\nUbp69WqS7y9rgoKCNGDAAEVHRyeK58yZU4UKFZKXl5fu3r2rq1evKjw8PMk8CxYs0JQpU5J8PEeO\nHPLx8ZGXl5du376t0NDQJG9EmjdvnqKiotS3b99kv46kDB8+XLt377aI3/+eubq66urVq7py5YrF\n9wCph2Y3gEytTJkyWrdundasWaNevXoZNtp8xYoVD0abf/rpp4w2BwAAAAAAyCKSWulbrly5ZB1v\nNps1dOhQq43u7Nmzq23btmrZsqWKFy+e6LGwsDCtX79e8+bN0927dxM9dv36dQ0aNEjff/+9smXL\nlsxXkrE9Ou65du3aeu+991StWjWLz+KCgoI0e/ZsbdmyxSLPhAkT1KBBgyTHz1vz5ZdfWm10586d\nWx07dtSLL76o/PnzJ3rs1KlTWr16tVatWvVgb+Lp06cn+7pIS7/++muSje5nnnlG7733nmrWrJlo\nv+Po6Gjt3LlT3333nU6cOGFx3DfffKNKlSqpSpUqVvPWr19f8+bNSxSbM2eOdu7cmSjWsWNH1a9f\nP8navby8JEnjx49PtHfztWvX1L9//0TPzZcvnyZMmJBkLkkWP0ejLViwwGqj22QyqWnTpnrjjTfk\n5+dn8b69/36fP3++RRN35syZqlKlil17QY8ePVrXr19/8HW1atX0/vvvq0aNGhZTKi5evKgdO3Yk\nK+/gwYMVFRX14OuGDRvq3XffVdWqVS32zw4ODtbRo0ctchw4cEDTpk2zmr9ixYrq0KGD6tWrJ1dX\n1wfx+yPfFy5cqL/++sviuKVLl8rf319NmzZN1uuwZtOmTTpz5syDr/PmzasPPvhAzz//vLy9vRM9\nNyoqShs3bkz16wv/odkNINNzcnLSq6++qhdeeEFfffWVxo0bZ8hdVZGRkRo4cKDmzZunqVOn6oUX\nXjCgWgAAAAAAHFx8lHTHtpGjcAC5S0umlI3rzkyuXbum3377zSLu5uamqlWrJivH0qVLrTbMixYt\nqkmTJqlUqVJWj/P29laHDh3UrFkz9evXT0FBQYkeP3nypAICAtS7d+9k1ZHRHThwQNJ/K02HDh36\n2CaVr6+vJkyYoG+//VZz585N9NitW7f0+++/64033kjWedeuXWt15WbFihU1ceJEFShQwOpxZcuW\n1YABA9SsWTP16dNHt2/fVkxMjI4cOZKs86aV0NBQjRs3ziLu7Oyszz77TG+++abV41xdXfX888+r\nQYMGmj59uhYsWJDo8fj4eA0ZMkRLliyxemOBl5fXg0b1w7FHFS1aVP7+/k98HeXLl0/0dUhIiMVz\nsmfPnqxcqeWff/7R9OnTLeLFihXT2LFjH3sjxP33e4sWLdS7d+9ENxgkJCRo6NChWrZsmXLlymVT\nbfebtiaTSQMGDHjs+6No0aJ65513UpTX1dVVY8aMUYMGDZJ8bpkyZVSmTJlEsYiICA0dOvTBDSMP\n69ixo7p06SKTyWTxmIuLi+rUqaM6derohx9+0MSJEy0mYYwZM0ZVqlSxaEwn18ON7vr162vkyJFJ\nfv/d3NzUokULm86DlKPZDSDLuD/avH379urZs6d+/fVXQ/IGBQWpadOmatWqlSZNmmRx1y0AAAAA\nAFnKndPSr37pXQVSy0tHJM9K6V1FuoiLi9MXX3xhdRHFCy+8kKymU0REhGbOnGkRz58/vwICAlSk\nSJEn5vDx8dG0adPUsWNHnT9/PtFjS5YsUevWrVW4cOEn5nEEzs7OmjhxomrXrp2s53fr1k1///33\ng0b5fWvXrk1Wszs2NlZTp061iJcoUUJTpkyRp6fnE3NUrVpVkydPVrdu3TLkGOMZM2ZYHfc8YMAA\ntWrV6onHu7i4qGfPnoqLi9OSJUsSPXbp0iUtWbJEnTt3NqxeR3W/If3ovs4lSpTQd999Jw8Pj2Tl\nyZ8/v2bOnKl27doler+HhYXpxx9/VLt27eyqc/DgwYY3ZZ2dnTV58mTVrFkzxccuXrxYoaGhFvEO\nHTqoW7duycpxvzH/6Kr+O3fuaMaMGRo6dGiK63pY7dq1NWHCBIuV6kg/zuldAACktdKlS2vt2rX6\n+eefDd3HaNWqVapQoYLGjBmTIf+QBQAAAAAAgG1Onz6tjh07av/+/RaPubm5qWvXrsnKs3btWosR\n5JI0cODAZDW67/Py8tLw4cPl5OSUKJ6QkPDYfZgdzXvvvZfsRvd91vYyPnbsmGJiYp547ObNmy32\nEXZyctKQIUOS1ei+r3LlyurQoUOyn59Wbty4oT/++MMi3rBhw2Q1uh/Ws2dPi1W50n+fkcbFxdlc\nY2axZcsWi5tRXF1dNXny5GQ3uu9zd3fX6NGjLd7vy5cvt2imp8Rzzz2XKquP33nnHZsa3bGxsVq9\nerVFvHz58vr4449TXEPdunUt4hs2bNDNmzdTXNt97u7uGjx4MI3uDIZmN4AsycnJSa+88oqOHTum\nIUOGJNrfwx6RkZEaNGiQKleurA0bNhiSEwAAAAAAAMb7559/kvwnMDBQf/75p2bPnq0uXbro7bff\ntrq3rJOTk4YNG6ZChQol65zLly+3iNWsWVONGjVKcf3+/v5q3ry5Rfznn3/OFAsx3Nzc1L59+xQf\nV7NmTYvGdFxcnIKDg5947I8//mgRa9y4cZL7UD/O+++/n+TI8/Ty008/WTT9TSaT+vTpk+JcLi4u\n6tu3r0X82rVr+vPPP22uMbNYuHChReydd95RsWLFbMpXvnx5i73MQ0NDtW/fPpvySUr2TTopkT17\ndn344Yc2Hbtp0yaLm00kqW/fvnJ2Tnk7s1+/fhbHRUdHW91DPblef/11m8egI/XQ7AaQpeXIkUPD\nhw/X0aNHDb2L7eTJk2rWrJlatWplcQcfAAAAAAAA0t8HH3yQ5D8fffSRPvvsM82cOdNiJPZ9bm5u\nGjVqlJo0aZKs84WEhFj9nOj111+3+TVYW417+/Ztq415R/Pcc8+leAWs9N8IZWt7IT/pM7qoqCir\nP+tXX301xTVI/63iffHFF206NrVY24v8mWeeSdFUgYfVrFnT6paO1s6TlYSGhuqff/5JFHNyclLr\n1q3tyvvyyy9bxA4ePGhTrkqVKlldmW+vhg0bpmgKwsP27NljEXvqqaf09NNP25SvePHiVleYWztP\nctn6+wCpi2Y3AOi/0ea//PKL1qxZo5IlSxqWd/Xq1SpfvrxGjx6dKe6oBQAAAAAAyOpMJpOaNm2q\nZcuWqWnTpsk+7vDhwxYxV1dXNWjQwOZaqlSpYnV/bmvncjRVq1a1+Vhrq2et7VP9sOPHj1uMhM6T\nJ49q1aplcx0vvPCCzccaLS4uTseOHbOIp+QatsZaQ//RRm9WY+2mCT8/P7tXBFt7T9j6Xq9Ro4Zd\ntSSlevXqNh9r7bXYe31am35x7Ngxm8a/58uXz9DeAYxDsxsAHtKyZUsdPXpUw4YNk5ubmyE57927\npy+++EL+/v767bffDMkJAAAAAACAtOfq6qrhw4dr9OjRKV4Ne+TIEYtY2bJl7f4Mys/PzyKWGZqN\npUqVsvlYd3d3i9iTmt3WVsP7+vrKZDLZXEe5cuWULVs2m483UnBwsKKioizi1q6flPD397eI/fvv\nv7p9+7ZdeR3Z33//bRGrUKGC3Xnz589vsR3nqVOnbMplRD1G5r1165bV6Qv2Xp/Wjo+MjEzWtgaP\nKl++vF21IPWwgzoAPCJHjhwaOnSo2rVrp969e+uXX34xJO+pU6fUvHlzvf766/r6669VokQJQ/IC\nAAAAAAAgbURHR+t///uf9uzZo0GDBil79uzJPjY0NNQi5uvra3dNvr6+2rBhQ6LY5cuX7c6b3vLk\nyWPzsY82BCVZ7FX9qJCQEItY2bJlba5B+m9f65IlS+rkyZMpOu7EiROKjY1N8fnc3d2TvEnA2jXh\n5uZmdQx5Sli7hs1ms8LCwuz6GTqy06dPW8RMJpMhN6G4ubklmiBq600FBQsWtLsWa2xdvZ7U7yx7\nf0cWL15cOXLk0L179yzOl9LcqfU9g/1odgNAEkqVKqU1a9Zo7dq16tWrl86cOWNI3h9//FG//fab\nvvjiC/Xr18/qH98AAAAAAABIXYGBgVbj0dHRun37tk6fPq2dO3dq7dq1unPnTqLnrF27VtevX9ek\nSZPk4pK8j9kfzSH9t1LTXgUKFEjWuRxNjhw5DM1nNpsf+7i171nevHntPq+Xl1eKj+nfv7/VmyOe\npFq1apo1a5bVx6w1RfPlyydnZ/sGAOfNm1cmk8liLHRWXtl969Yti9jSpUu1dOlSw88VHx+viIgI\n5cqVK0XHpfT5qZ3X2vvP2dnZ7vegs7Oz8uXLp4sXLz7xfE+SWt8z2I9mNwA8QYsWLdSkSRONGzdO\nY8aMsTruJ6Xu3bun//3vf5o/f76mTJlide8QAAAAAAAcUu7S0kuW45qRSeQund4VpDpXV1cVKFBA\nBQoUUO3atdWxY0cNGzZMO3bsSPS8Xbt2acKECRo4cGCy8lpr/lkbt51S1howWbnRaCtrza/U+vmk\nh9S6/qT/XuOjDd7McMOFraw1u1OTLc1uo7bwNCqvteszZ86ccnJysrckw35Hptb3DPaj2Q0AyeDm\n5qYhQ4Y8GG2+Zs0aQ/IGBwfrpZde0muvvaavv/5aTz31lCF5AQAAAABINyY3ybNSelcBGMbT01MT\nJ05Unz59tHPnzkSPrVy5UrVr11ajRo2emOfh0cP3GTHxz1qOR0f24smsjTk3Yr/tlIy6T02pdf0l\nlScrX4NP2h/eaAkJCWl6vtTA9Ql72DefAgCymJIlS+rnn3/W2rVrk9z/xhY//fSTKlSooJEjRxqy\nchwAAAAAAADGMZlMGjVqlHx8fCweGzNmTLKaW9ZW0UZGRtpdm7UcGWU1sSOx9j27e/eu3XnTuvGZ\nFGvXnxGvL6k8WfkaNJlM6V2Cw0mt349J5cnK12dmxMpuALDByy+/rMaNG2v8+PEaPXq0IQ3qqKgo\nDR48WPPnz9fUqVMZbQ4AAAAAAJCB5MqVS59//rl69uyZKB4eHq45c+aod+/ejz0+T548FrHUaqZ6\neHjYnTel4uLi0vycRsqdO7dFzIhGtS0/419++cXu8z4qta4/s9lstZlo7XxZhbu7u8WkgIEDB+rN\nN99Mp4oyPmvXy7179xQfH2/3zQMZ5XckUg8ruwHARm5ubho8eLCOHz+u1157zbC8p0+ffjDa/Ny5\nc4blBQAAAAAAgH3q1q2revXqWcSXL1+uy5cvP/ZYa83US5cu2V3TxYsXk3Wuh7m4WK6Di4+Pt6sO\nR98n3NPT0yJ24cIFu/P++++/ducwgrVm4rVr16yOj06JS5cuyWw2J+t8WYW3t7dF7ObNm2lfiANJ\n6ndWSEiIXXljYmJ05cqVZJ8PjolmNwDY6amnntKPP/6oX3/9VaVLlzYs788//6wKFSpoxIgRjDYH\nAAAAAADIIHr06CEnJ6dEsZiYGM2ZM+exx1nbEi8oKMjueqzleNL2ezlz5rSI2bOH7c2bN+1umqa3\nsmXLWsROnjxpV87r168rPDzcrhxGKVmypEUsPj5ewcHBduU9ceKERSx79uwqWrSoXXkdmbXv9ZNu\nhsnqihUrpmzZslnE7f0dGRwcbPVGHiO3KEX6o9kNAAZp3ry5jhw5ohEjRihHjhyG5IyKitKQIUPk\n5+endevWGZITAAAAAAAAtitbtqyef/55i/jatWsfu1Lb39/fInbu3Dm7mqGxsbE6fPhwss71MGv7\n1dpTx6FDh2w+NqPw8/OziJ07d87qqtDk+uuvv+wpyVBFihRRvnz5LOIHDhywK+/+/fstYuXLl7fa\nuMwqKleubBELDAxMh0ocR/bs2eXr62sRt3Z9pYS173v+/Pnl4+NjV15kLDS7AcBAbm5u+t///qfj\nx4/r9ddfNyzv6dOn1aJFC7366qs6e/asYXkBAAAAAACQcp07d7ZY3R0XF/fY1d3+/v4WxyQkJOj3\n33+3uY5t27ZZHR9urdn2sLx581rsgxseHq7r16/bXIejK1q0qEUz2N6fz6+//mpvWYaydl2sX7/e\n5nyxsbHasGGDRfxJN1tkdvXr17eIXbx4UadOnUqHahyHtevzjz/+UFxcnM05rb0Hs/r1mRnR7AaA\nVFCiRAmtXr1a69evV5kyZQzLu2bNGlWsWFHDhw+3a7QUAAAAAAAAbFemTBk1atTIIv7rr79a3UNb\n+m+P2Fq1alnEV65cqdjY2BTXYDabtWTJEot4yZIln7jVnpubm0qUKGER37NnT4rrCA8P12+//Zbi\n4zKil156ySK2bNkym7YYPHHihE3fz9TUuHFji9jJkydtXnW8du1a3bp1yyLepEkTm/JlFj4+PqpW\nrZpFfNasWelQjeOwdn3evHnT5ptG9uzZY3VMf1a/PjMjmt0AkIpefPFFHTlyRCNHjjR0tPmwYcPk\n5+entWvXGpITAAAAAAAAKdOpUyeLWHx8/GNXd7/99tsWsfPnz2vx4sUpPv+6deusjg9v3bq1xQpy\naypWrGgR++mnn1Jcx6hRoxx+v+77rE1qvHz5subOnZuiPPHx8Ro3bpwSEhKMKs0QTZo0sTrKfPz4\n8SlePXvz5k1NmzbNIl6xYkVWzkpq27atRWzz5s2Z5saQ1FClShWVL1/eIh4QEKCIiIgU5YqNjdX4\n8eMt4gUKFLDaVIdjo9kNAKnM1dVVX3zxhY4fP6433njDsLxnzpxRy5Yt1bJlS505c8awvAAAAAAA\nAHgyX19fNWjQwCK+fv16nT9/3uox9evXV/HixS3iM2bM0I4dO5J97sOHD2vs2LEWcQ8PD7388svJ\nymGt4XPgwIFkr6I0m8365ptvMsUI8/uKFy+uhg0bWsTnz5+vdevWJSuH2WzWiBEjrO6lnt5cXFz0\n1ltvWcRPnz6t4cOHy2w2JytPVFSU+vXrZ3VVd5s2beyuMzNo2LChatSoYRH/8ssvtWXLFrvz3759\n26abZDI6a9dPeHi4+vfvr5iYmGTlSEhI0ODBg/Xvv/9aPNa6dWu5uLjYXScyFprdAJBGSpQooVWr\nVum3335T2bJlDcu7du1aVaxYUcOGDWO0OQAAAAAAQBrq3LmzRexxq7udnZ01ZMgQOTsn/mg+Li5O\nAwYM0OrVq5/YcNywYYN69epl9XOggQMHKmfOnMmqvW7duipQoIBFfMSIEU9s7F68eFH9+vXTwoUL\nJf33urJnz56s82Z0n332mdzd3RPFzGazvvzyS02bNu2xDbcrV66od+/eiaYxurm5pVqttnj//fet\nbru4fv16ff7557p58+Zjj7948aK6d++ugwcPWjxWr149vfjiiwZV6viGDh2qXLlyJYrFxMSoX79+\nGjNmjK5evZqifPHx8QoMDNTo0aP10ksvKSAgwMhyM4TmzZurdu3aFvF9+/apZ8+eCg0Nfezx169f\nV//+/bVx40aLx8qVK6f33nvPsFqRcXD7AgCksWbNmumff/7RpEmTNGLECEMa1NHR0Ro+fLgWLFig\nb775Ri1btjSgUgAAAAAAADxOhQoV9Oyzz2r79u2J4r///rs6duxodV/sqlWrqn379po3b16ieHR0\ntEaPHq2ffvpJLVq0UK1atZQ/f36ZTCZdvXpVBw8e1Lp167R//36rtbz00kt64YUXkl27yWRSt27d\n9OWXXyaKx8bGaujQoVq2bJmaNGmikiVLKleuXLp9+7ZCQkK0Z88e7d27N9HY644dO2rt2rVPbEQ5\nAm9vb/Xu3VujRo1KFI+Pj9f8+fO1Zs0aNWnSRP7+/ipQoIBiYmJ05coV7dq1Szt37kw00r1ixYoq\nUaKE1q9fn9YvI0nZs2fXyJEj9f7771s07jdu3KjAwEC1aNFCzz33nIoUKSIPDw/duHFD586d08aN\nG/Xrr79a3cPcy8tLQ4YMSauX4RB8fHw0btw49erVS7GxsYkeW7VqlX7++Wc1bNhQNWvWlJ+fn/Ln\nz688efJIkiIiIhQREaELFy4oODhYQUFB2rt3b6LV9JnlBpOHOTk5adiwYXr77bctJgcEBgbq7bff\nVvPmzdWkSROVKFFCXl5eunXrli5evKjNmzcnuY+8q6urRo4cqWzZsqXVS0EaotkNAOnA1dVVn3/+\nudq2bas+ffpo1apVhuQ9e/asXnnlFb388sv65ptvVLp0aUPyAgAAAAAAwLpOnTpZNLvvr+4eMWKE\n1WM++ugjnT9/Xps2bbJ47NixYzp27FiKaqhWrZoGDRqUomMk6ZVXXtGmTZu0c+dOm+to1qyZOnfu\nnGg1s6N7/fXXdebMGS1dutTisevXr2v58uVavnz5Y3PkzZtXX331lWbNmpVaZdqsTJkyGjFihAYN\nGqT4+PhEj928eVOLFi3SokWLkp3P3d1dkyZNsrofeFZXq1Ytff311/rss88UGRmZ6LG4uDht2rTJ\n6u+BrCx//vyaOHGievbsafE9i4yM1KpVq1L0ebqLi4tGjRqlUqVKGV0qMgjGmANAOipevLhWrlyp\n33//XeXKlTMs77p161SpUiUNHTqU0eYAAAAAAACpqFKlSqpbt65F/Pfff9e5c+esHmMymTRq1Ci9\n++67dp+/efPmmjJlis3jsseOHWt1bHBytGrVSsOHD7cYy54Z9O3bV126dLHptRUqVEjffvutChcu\nnAqVGaNx48b65ptv5OHhYVeeIkWKaPbs2fL39zeossyndu3aWrBggSpWrGho3sy893TVqlU1a9Ys\n+fj42JXH09NTU6dOVaNGjYwpDBlS5vsvEAA4oKZNm+rw4cMaM2ZMsvdVepLo6Gh9+eWXqlixotas\nWfPE/Z4AAAAAAABgmy5duljEEhISNHv27CSPcXFxUd++ffXtt9/atAiiePHiGjdunEaMGGHXvtBu\nbm76+uuv9dFHH1nsVZ2UIkWKaPz48fr8888zdcOtS5cuKfr5mEwmvfrqq1qyZIlDTFysXbu2li9f\nrpYtW8pkMqXoWDc3N7Vr105Lly41dBFPZvXUU09p/vz5Gjx4sIoXL25XrgoVKqhv3776+eefDaou\nYypfvrx++OEHtWnTRq6urik61mQy6ZVXXtGKFStUs2bNVKoQGYWTme5HqqtevbouX76sQoUKJbmf\nCgDcd/78efXt21crV640NO9LL72kb775RmXKlDE0LwAAAADA8Z06dUpxcXFycXFR2bJl07scwFBh\nYWG6cuWKRdzolajHjx9PtI+1JDk7O6tSpUrJOj4wMFAbNmxQYGCgLly4YHXhQuHChfX000/rhRde\nUN26dQ1fUX3z5k1t3rxZu3bt0unTp3Xz5k3dvXtXOXLkkI+PjypUqKAGDRro2WefTXFz1JGZzWbt\n27dPmzdv1uHDh3Xp0iXdu3dP2bJlk5eXl0qWLKkaNWqoadOmKlSoUHqXa5PLly9r/fr12rlzp44f\nP55o7/H73N3d5efnp2effVYvvviiPD097TrnokWLtHfv3kSxtm3b2jRpIDw8XMOGDUsUy5s3r4YP\nH25PianCbDbrwIED2rJliw4dOqTg4GCL/dPvy5Mnj0qUKKEyZcqoevXqqlmzZpYcF3/jxg399ttv\n2r59u44ePaq7d+9aPMfV1VUVK1ZUvXr19OKLLzrsezE9OPrfgTS70wDNbgC2+OOPP/TJJ58oKCjI\nsJzZs2fXgAEDNHDgQMNWkAMAAAAAHJ+jf8gJZDbR0dEKCwt70NDJkSOHvL29lSNHjnSuDFmB2WzW\nlStXdOvWLcXGxip79uzKmzdvlmyypgWz2azw8HDdvHlT0dHRyp49u3LmzKncuXMrT5486V1ehnTt\n2jXduHFDMTExypYtmzw9PVWgQAE5OTmld2kOydH/DqTZnQZodgOwVUxMjL7++mt9+eWXioyMNCxv\niRIl9M033+iVV17hDwAAAAAAgMN/yAkAAADbOPrfgezZDQAZ2P2V2CdOnNBbb71lWN5///1Xr732\nml5++WUFBwcblhcAAAAAAAAAACCt0OwGAAdQrFgxLV++XH/88YfKly9vWN7169erUqVKGjx4sKEr\nxwEAAAAAAAAAAFIbzW4AcCBNmjTRoUOHNHbsWLm7uxuSMyYmRiNHjlTFihX1008/id0tAAAAAAAA\nAACAI6DZDQAOJnv27Prss8904sQJtW7d2rC8//77r15//XW99NJLOnXqlGF5AQAAAAAAAAAAUgPN\nbgBwUEWLFtWyZcu0ceNGVahQwbC8v/32m/z8/PTFF1/o7t27huUFAAAAAAAAAAAwEs1uAHBwjRs3\n1sGDBzVu3DhDR5uPHj1aFStW1OrVqxltDgAAAAAAAAAAMhya3QCQCWTPnl39+/fXiRMn9PbbbxuW\n9/z582rVqpWaN2+ukydPGpYXAAAAAAAAAADAXjS7ASATKVq0qH744Qdt2rTJ0NHmv//+u/z9/TVo\n0CBGmwMAAAAAAAAAgAyBZjcAZELPP/+8Dh06pAkTJihXrlyG5IyJidGYMWNUoUIFrVq1itHmAAAA\nAAAAAIAsgc/DMy6a3QCQSWXLlk19+/bViRMn9O677xqW98KFC3rzzTf14osvMtocAAAAAAAAAJCp\n3blzR8eOHdPt27fTuxRYQbMbADK5IkWKaMmSJfrzzz9VsWJFw/Ju2LBBfn5++vzzzxltDgAAAAAA\nAADIVGJiYnTmzBkFBQXp3r17On/+vBISEtK7LDyCZjcAZBHPPfecDh48qIkTJxo22jw2NlZfffWV\nypcvr5UrVzLKBQAAAAAAAADg0BISEhQWFqYjR47o+vXrD+JRUVG6cuVKOlYGa2h2A0AWki1bNvXp\n00dBQUFq06aNYXkvXryot956S02bNtWJEycMywsAAAAAAAAAQFq5c+eOjh8/rgsXLlhdxR0SEqKY\nmJh0qAxJodkNAFlQ4cKFtXjxYm3evFmVKlUyLO/GjRtVuXJlDRw4UBEREYblBQAAAAAAAAAgtTw6\nsjwpCQkJunDhQhpWhieh2Q0AWVijRo30999/a9KkScqdO7chOWNjYzV27FhVqFBBK1asYLQ5AAAA\nAAAAACBDSkhI0OXLly1Glj/OjRs3dPv27VSuDMlFsxsAsrhs2bLp008/VVBQkNq2bWtY3osXL6p1\n69Z64YUXGG0OAAAAAAAAAMhQ7o8sv3jxotWR5Y9z/vz5FB+D1EGzGwAgSfLx8dGiRYu0ZcsW+fn5\nGZZ306ZNqly5sgYMGMBocwAAAAAAAABAukruyPLHiYqK0pUrVwyuDLag2Q0ASKRhw4Y6cOCAvv76\na0NHm48bN07ly5fX8uXLGW0OAAAAAAAAAEhTtowsf5yQkBDFxMQYUBnsQbMbAGAhW7Zs6t27t4KC\ngvTee+8ZlvfSpUt6++231aRJEx0/ftywvAAAAAAAAAAAJOXOnTs6duyYTSPLk2I2m5lmmgHQ7AYA\nJMnHx0cLFy7Utm3b5O/vb1jeP//8U5UrV1b//v11584dw/ICAAAAAAAAAHDfwyPLo6KiDMubJ08e\nVapUSXnz5jUsJ2xDsxsA8ETPPvusDhw4oMmTJytPnjyG5IyLi9OECRNUvnx5/fDDD4w2BwAAAAAA\nAAAYwuiR5fdlz55dpUuXVtmyZeXm5mZYXtiOZjcAIFlcXFzUq1cvBQUFqV27doblDQkJ0bvvvqvG\njRvr2LFjhuUFAAAAAAAAAGQ9t2/fNnxkuZOTk3x8fFSpUiV5eXnJycnJkLywH81uAECKFCpUSAsW\nLND27dtVuXJlw/Ju3rxZVapUYbQ5AAAAAAAAACDFYmJidPr0aZ08eTJVRpYXKVJEJpPJsLwwBs1u\nAIBN6tevr/3792vKlCmpMtp86dKljDYHAAAAAAAAADzWwyPLb9y4YVheRpY7BprdAACbubi46JNP\nPtHJkyfVvn17w/KGhISoTZs2ev7553X06FHD8gIAAAAAAAAAMg9GloNmNwDAbt7e3po/f7527Nih\nKlWqGJZ3y5Ytqlq1qvr168docwAAAAAAAACAJEaW4//Q7AYAGKZevXoKDAzUlClT5OHhYUjOuLg4\nTZw4Ub6+vlqyZAmjzQEAAAAAAAAgi2JkOR5FsxsAYKj7o82DgoLUoUMHw/KGhoaqbdu2eu6553Tk\nyBHD8gIAAAAAAAAAMj5GlsMamt0AgFTh7e2tefPmaefOnapataphebdu3aqqVauqT58+un37tmF5\nAQAAAAAAAAAZT2qNLPfw8GBkeSZAsxsAkKrq1q2rffv2aerUqYaNNo+Pj9fXX38tX19fLV68mNHm\nAAAAAAAAAJDJJCQkKDQ0NFVGlpcpU0ZlypRhZHkmQLMbAJDqXFxc1KNHD508eVIffPCBYXkvX76s\n9957T40aNdI///xjWF4AAAAAAAAAQPq5P7L80qVLqTKy3NPTk5HlmQTNbgBAmilYsKC+++477dq1\ny9DR5tu2bdPTTz+tTz/9VLdu3TIsLwAAAAAAAAAg7TCyHClFsxsAkObq1KmjwMBABQQEyNPT05Cc\n8fHxmjx5snx9fbVo0SJGmwMAAAAAAACAg2BkOWxFsxsAkC5MJpM+/vhjnTx5Uh9++KFhecPCwtSu\nXTs1bNhQhw8fNiwvAAAAAAAAAMB4t27dSrWR5X5+fowsz+RodgMA0lWBAgU0d+5c7dq1S08//bRh\nebdv365q1aqpd+/ejDYHAAAAAAAAgAwmOjpap0+f1qlTp1JtZLmzM63QzI6fMAAgQ6hTp4727dun\n6dOny8vLy5Cc8fHx+uabb+Tr66sFCxYw2hwAAAAAAAAA0tn9keVHjx41dGS5q6urypQpo7JlyzKy\nPAuh2Q0AyDBMJpO6deumoKAgdezY0bC8YWFhat++vRo0aKBDhw4ZlhcAAAAAAAAAkHypNbK8cOHC\nqlSpkjw9PQ3JCcdBsxsAkOEUKFBAc+bM0e7du1WtWjXD8u7YsUPVqlVTr169dPPmTcPyAgAAAAAA\nIHX98ssvqlGjRqJ/hg0blt5lAUim6OhoBQcHp8rIcj8/PxUuXJiR5VkUP3UAQIZVu3Zt/fXXX/r2\n228NG22ekJCgKVOmyNfXV99//71hdw8CAAAAAAAAABJ7eGS5kQuQHh5Z7urqalheOB6X9C4AAIDH\nMZlM+uijj/Tmm29q0KBBmjNnjiF7b1+5ckUdOnTQ7NmzFRAQoCpVqhhQLQAAAAAASE8hISF65ZVX\n0rsMSdKaNWtUuHDh9C4DANLNrVu3dP78eUVHRxuW08nJST4+PipUqBAruSGJld0AAAeRP39+zZo1\nS3v27FGNGjUMy7tz505Vq1ZNPXv2ZLQ5AAAAAABwWFeuXNGuXbsS/RMcHJzeZQHIgh4eWW5ko5uR\n5bCGKwEA4FBq1aqlPXv2aMaMGcqbN68hORMSEjR16lRGmwMAAAAAAIe1d+9e9ezZM9E/ixYtSu+y\nAGQhjCxHeqDZDQBwOCaTSV27dtXJkyfVpUsXOTk5GZL3/mjzZ599VgcPHjQkJwAAAAAAAABkdrdu\n3dLRo0d16dIlwxYTOTk5qXDhwqpUqZI8PT0NyYnMhz27AQAOK1++fJo5c6Y6deqkjz/+WIGBgYbk\n3bVrl6pXr65u3bppxIgR8vLyMiQvAAAAAABIXfnz59e8efNsOvarr75SUFBQopivr68GDhxocy0A\nkNlFR0frwoULhm8R6enpqWLFirGSG09EsxsA4PBq1qypPXv2aO7cufr88891/fp1u3MmJCQoICBA\ny5cv19ixY9W+fXv2gQEAAAAAIIPLnj27/P39bTrW3d3daszWfACQmSUkJOjy5cu6fPmyodtCurq6\nqlixYqzkRrLxqT0AIFMwmUzq0qWLTp48qa5duxo22vzq1av68MMPVb9+fR04cMCQnAAAAAAAAADg\nqO6PLA8JCWFkOdIdzW4AQKaSL18+zZgxQ3/99Zdq1qxpWN7du3erZs2a6t69u27cuGFYXgAAAAAA\nAABwBNHR0QoODtapU6cUHR1tWF5PT0/5+fmpcOHCTNdEinHFAAAypRo1amjPnj2aPXu28uXLZ0jO\nhIQETZ8+XeXKldN3331n6HgeAAAAAAAAAMiIEhISFBISoiNHjhi6N7erq6vKli2rMmXKsDc3bMae\n3QCATMvZ2VmdOnXS66+/rv/973+aOXOmzGaz3XmvXbumjh07avbs2QoICFC1atUMqBYAAAAAAGRG\n0dHRCgoK0vnz53Xjxg1FR0cre/bs8vDwULFixVS+fHnlzJkzvctMsbi4OF28eFHnzp1TeHi4IiMj\nFRsbq9y5cytPnjwqWLCgKlSoIDc3t/QuNU3duHFDQUFBCg0N1e3btxUfHy9PT0/lzZtXxYoVU+nS\npdO8pnPnzun06dO6cuWKIiMjZTKZlCdPHtWpU0c+Pj425UxISFBwcLDOnj2ra9eu6d69e3JxcZGn\np6caNWqUojHUoaGhOnXqlEJDQxUZGSmz2aycOXPK29tbpUqVUokSJWyq0R43b97UiRMndOnSJd25\nc0dxcXFyd3dX6dKlVatWrTSvJz3dunVL58+fN3Qlt7OzswoVKqRChQqxkht2o9kNAMj08uXLp2+/\n/VYdO3ZU9+7d9ddffxmSd8+ePapRo4Y++ugjjRw5Unnz5jUkLwAAAAAAcGwJCQn6888/tWbNGu3b\nt0+xsbFJPtdkMqlKlSpq2bKlmjdvLheX5H9sX6NGjcc+vnbtWq1duzZZuQIDAx/7eEJCgv7++2/t\n2bNH+/fv17FjxxQXF/fYY1xcXFSxYkU1bdpUr732WqZtfIeHh+vHH3/UH3/8odOnTz/2ud7e3qpX\nr57atm1rcxP3l19+0fDhwxPFWrRooWHDhj34+vLly1q2bJl+++03Xb161WqeoUOHqmXLlg++njlz\npmbPnp3oOZ07d1bXrl0ffH327FktXbpUmzZt0q1bt6zmLVq06BOvzcuXL2vFihX6448/FBIS8tjn\n5suXT40bN1br1q311FNPPfa5j2Otpoev+7i4OK1du1Y//fSTjh07ZnWqY7Vq1bJMszs6OloXLlww\ndCW39N/I8mLFirGSG4ah2Q0AyDJq1Kih3bt3a968eRowYIDCw8Ptzmk2m/Xtt99qxYoV+uqrr/TB\nBx9wNyIAAAAAAFnYoUOHNHr06Cc2Pe+Lj4/XgQMHdODAAc2ePVsDBgxQvXr1UrnK5DObzZo4caI2\nbtyoa9eupejYuLg4HT58WIcPH9bcuXP18ccf6/XXX0+lStNeVFSU5syZo6VLlyZ71WtYWJhWr16t\nn3/+Wa1atdLHH3+sXLlyGVrXokWL9O233xq6EjcuLk7Tp0/X4sWLFR8fb3OeqKgozZw5U0uXLn3i\nzRL3hYeHa/ny5Vq5cqVeffVV9ezZU7lz57a5BmuOHz+uIUOG6OzZs4bmdUQJCQm6fPmyQkNDDZmS\neZ+rq6uKFy8uDw8Pw3ICEnt2AwCyGGdnZ3Xs2FEnT55Ut27d5OTkZEjea9euqVOnTqpbt672799v\nSE4AAAAAAOBYli5dqi5duiS70f2okJAQ9erVSwEBAQZXZrv4+Hj98MMPKW50P+rGjRsaNWqURo8e\nnewmZ0Z27tw5tWvXTvPnz7epqRwfH6/ly5erU6dOSa68Timz2azhw4dr8uTJhja6Y2Ji9Omnn2rB\nggV2NbrDwsLUsWNHLVy40KZrICEhQT/++KPatWtnaFN6586d6tSpE41u/Te+/ejRowoJCTGs0e3s\n7KwiRYqoUqVKNLqRKljZDQDIkvLmzavp06c/GG2+d+9eQ/Lu3btXNWvWVNeuXTVq1ChGmwMAAAAA\nkEUsWLBAU6ZMSfLxHDlyyMfHR15eXrp9+7ZCQ0MVERFh9bnz5s1TVFSU+vbtm1rlGiJbtmzy8fFR\nrly55O7urtjYWN25c0cXLlxQTEyM1WNWr14tV1fXDP/aHicoKEgff/xxkmO8pf/GlefLl0/u7u66\ndeuWLl26pLt371o8Lzg4WB9++KHmzp2rggUL2lXX9OnT9csvv1jECxQooPz58ytnzpwKDw9XWFiY\n7t27l+y8w4cP1+7duy3iPj4+yps3r1xdXXX16lVduXIlySb7tWvX1LVrV128eDHJ83h7e6tAgQJy\ncXHR1atXk2y4Xrx4UV27dtWsWbPsGmsu/fezHDBggEXdOXPmVKFCheTl5aW7d+/q6tWrhkyJzKii\no6N1/vz5x17TtmBkOdICzW4AQJZWvXp17dq1S/Pnz9eAAQPsvktZ+u8u2hkzZjwYbf7hhx8y2hwA\nAABAlmA2m3Xnzp30LgNpIHfu3IZNS8sMDhw4oGnTpll9rGLFiurQoYPq1auXqOETFxenffv2aeHC\nhfrrr78sjlu6dKn8/f3VtGnTJM87b968B/++Y8cOzZ07N9Hj9erVU6dOnVL6cpKUM2dOPfPMM3r2\n2WdVsWJFPfXUU1b3GI+Li9OJEye0du1arVmzxqLxvXTpUtWsWVMNGjQwrLa0cuvWLfXp08dqU7Bo\n0aJq27atGjRoIG9v70SPxcXF6cCBA5o3b5727duX6LHQ0FANHTpU06dPt/l9dfToUf37778PvnZ3\nd9d7772nZs2aqXjx4ha1bNu2TQUKFHhi3k2bNunMmTMPvs6bN68++OADPf/88xavMSoqShs3blT+\n/PkTxc1ms4YOHWq10Z09e3a1bdtWLVu2tKgzLCxM69ev17x58yxuFLh+/boGDRqk77//XtmyZXvi\n60jK4MGDFRUV9eDrhg0b6t1331XVqlUtru3g4GAdPXrU5nNlRIwsR2ZAsxsAkOU5Ozvrww8/1Guv\nvabBgwdrxowZSkhIsDtveHi4OnfurNmzZysgIEA1atQwoFoAAAAAyLju3LnDB9tZxK1bt5QnT570\nLiNDiIiI0NChQ61+ltCxY0d16dJFJpPJ4jEXFxfVqVNHderU0Q8//KCJEydaNJvGjBmjKlWqWDQV\n7/P393/w7+fOnbN43MvLK9FzbPXUU0+pTZs2eumll+Tm5vbE57u4uMjPz09+fn569913NXDgQJ06\ndSrRc6ZNm+aQze5hw4YpLCwsUczJyUnvv/++unXrZrX5L/33PalVq5Zq1aqllStXavz48YlGgu/b\nt0+LFy/We++9Z1NdD4/grlixoiZNmmTRdH64lueffz5ZeR9udNevX18jR45Mco9xNzc3tWjRwiK+\ndOlSq1MVixYtqkmTJqlUqVJW83l7e6tDhw5q1qyZ+vXrp6CgoESPnzx5UgEBAerdu3eyXos191+f\nq6urxowZ89hrskyZMipTpozN58pobt68qQsXLhg68t7Z2Vk+Pj7y9vZm8Q/SDFcaAAD/X968eRUQ\nEKDAwEDVqVPHsLx//fWXatWqpY8++ihTjzsCAAAAACArWrx4sUJDQy3iHTp0ULdu3aw2uh/1zjvv\nWB3rfefOHc2YMcOQOm3l4uKiFStW6I033khWo/tRJUqU0LfffqsiRYokip85c0Z79uwxqsw0sX79\nem3fvt0i3r9/f33yySdJNrof9eabb2rAgAEWcVv3/35Y2bJl9e233ybZ6LZV7dq1NWHChCQb3UmJ\niIjQzJkzLeL58+dXQEBAko3uh/n4+GjatGkWK78lacmSJQoJCUlRTY9ydnbW5MmTHfLmC1tER0fr\n1KlTCg4ONrTR7eXlpUqVKsnHx4dGN9IUVxsAAI94+umntWPHDn333XfJGueUHGazWTNnzlS5cuU0\ne/ZsQ1aOAwAAAACA9BUbG6vVq1dbxMuXL6+PP/44Rbneeecd1a1b1yK+YcMG3bx509YSDWHvyHpP\nT0+rzfzffvvNrrxpbcGCBRaxV199Va1bt05xrjfeeEMNGzZMFLt586bWr19vc30mk0lDhw6Vu7u7\nzTmscXd31+DBg5PdzH/Y2rVrre5VPnDgQIsbIB7Hy8tLw4cPt7gWExIStGLFihTX9bB33nlHNWvW\ntCuHI0hISFBISIiOHDli6N7cbm5uKlu2rEqXLs3e3EgXNLsBALDC2dlZH3zwgYKCgtS9e3fD7ka8\nfv26unTpotq1a1vszwQAAAAAABzLpk2brE5x69u3r02fJfTr18/iuOjoaP3000+2lphh1KtXT56e\nnolihw8fTp9ibLB7926LUezu7u7q3r27zTk7d+5sEVuzZo3N+Ro2bKjy5cvbfHxSXn/99SRH6T/J\n8uXLLWI1a9ZUo0aNUpzL399fzZs3t4j//PPPNq9Qzp49uz788EObjnUkN2/e1NGjRxUSEmLY3tzO\nzs4qUqSIKlasyBYmSFc0uwEAeAwvLy9NmzZN+/fvt3p3ta327dunZ555Rl26dNG1a9cMywsAAAAA\nANKOtTHcTz31lJ5++mmb8hUvXtzqClNHG/dtjclksmjEXrhwwdAVpqlpw4YNFrGmTZsqb968Nucs\nX768xRjv48eP29y4ffXVV22uJTXyhoSE6Pz58xbx119/3eZaWrVqZRG7ffu2jh49alO+hg0bWtyE\nkZkwshxZAVcgAADJULVqVW3fvl3z5s0zdLT57Nmz5evrq5kzZyo+Pt6QvAAAAAAAIG1YW5nctGlT\nu3JaW7l67NixTPG5gZeXV6KvzWazLl26lE7VpMyBAwcsYs8//7zdeatWrZro69jYWB0/fjzFeZyd\nnVWtWjW763lUvnz5VLJkSZuOtfb+cHV1tWtv7CpVqqhw4cLJOldyVK9e3eZaMrLUHFlerlw5RpYj\nQ0n5BgsAAGRRzs7O6tChg1577TUNGTJEAQEBhuy9ff36dX300UeaM2eOAgICVKtWLQOqBQAAAAAA\nqenWrVtWV636+fnZldfa8ZGRkQoODpavr69duY0SGRmpXbt26cSJEwoODtbFixcVERGhyMhI3bt3\nL0Vjku/cuZOKlRrjypUrVpvyFSpUsDu3tcbtqVOnLJrgT/LUU08pR44cdtfzKHvGoh85csQiVrZs\nWbm5udlTkvz8/BQSEpIo9s8//9iUy4ifYUZiNpt169YtXbhwwdCV3M7OzvLx8ZG3tzcruZHh0OwG\nACCFPD09NWXKFH344Yfq0aOHdu7caUjewMBA1a5dWx07dtSYMWOUP39+Q/ICAAAAAADjXb582Wrc\n3oZ08eLFlSNHDt27d8/ifOnd7A4ODtZ3332nbdu2KSoqypCcjtDsPn36tEUsZ86cunDhgi5cuGBX\nbmuv35aVuAULFrSrjtTIGxoaahEz4hr29fW1GCuf1PvxSWzdizwjioqKSpWtAby8vFSsWDFlz57d\n0LyAUWh2AwBgo/ujzRcuXKj+/fvrypUrduc0m82aM2eOVq1apdGjR6tz584ymUwGVAsAAAAAAIxk\nrUnp7Oxs1x7O93Pky5dPFy9efOL50kpcXJymTZumpUuXGj5O3aimeWqy1jyMjIzUBx98kCrnu337\ndoqPyZUrVypUYl9ea9esEYs7rG0xaOv7I7W+b2kpPj5ely9f1uXLl1M0VeFJ3NzcVLx4ceXJk8ew\nnEBqYNYAAAB2cHJy0vvvv6+goCD17NnTsDE+N27cULdu3fTMM89o7969huQEAAAAAADGsdaQzJkz\np5ycnOzOba0BZ0sD1AhxcXH6/PPPtWjRolTZN9zI5lxqMXql7JNERESk+Bh7R4OnRl5r16y7u7s9\n5Ugy9v2RWt+3tGA2m3Xz5k0dPXpUoaGhhr2XnJ2dVaRIEVWsWJFGNxwCK7sBADCAp6envvnmmwej\nzXfs2GFI3v379ycabW7tzlUAAAAAAJD2rO2H6+rqakhua3keHWueVqZOnarNmzdbfczV1VWVKlVS\nxYoV5e3trYIFCypHjhzKnj271dcwZ84cw7aDS0tpvao+ISEhTc+XWlLrPZKR3h/phZHlwP+h2Q0A\ngIGqVKmibdu2adGiRerfv7/CwsIMyTt37lytXr1ao0aNUpcuXRhtDgAAACBDyp07d5qvgET6yJ07\nd3qXkO6srVCNjIw0JLe1POkxbvnMmTP64YcfLOIeHh766KOP1KJFC+XIkSPZ+Rx1laiLC60UW6TW\neySjvD/SAyPLAUv8hgYAwGBOTk5q166dXnnlFQ0dOlRTp0415I7cGzdu6OOPP9acOXMUEBCg2rVr\nG1AtAAAAABjHycmJD8qRZVi71u/du6f4+Hi7b1K3Nsbaw8PDrpy2WLlypcXo8nz58mnevHkqXLhw\nivOl1yh2e1lr2ubNm1cbNmxIh2och7X3yN27d+3Om1HeH2np/sjyCxcuKCYmxrC8zs7OKly4sAoW\nLGjY9oxAWuPKBQAglXh4eGjy5Mn6+++/Vb9+fcPyHjhwQHXq1FHHjh119epVw/ICAAAAAIDkS2p1\ne0hIiF15Y2JidOXKlWSfLzVt377dItanTx+bGt2SdPPmTTsrSh/e3t4WMaZYPJm1a/bSpUt25714\n8WKyzpVZREVFKTg4WKdPnza00e3l5SU/Pz8VKlSIRjccGlcvAACprHLlytq2bZsWLlxo9X+ObPXd\nd9+pXLlymj59usVd1gAAAAAAIHUVK1ZM2bJls4gHBQXZlTc4ONjq/+eXKlXKrrwpdfPmTYWGhiaK\n5cyZU88995xN+eLi4hQcHGxEaWnO2vc+Pj7e6k0J+D/Wvm/2vj+SypHW74+0EB8fr0uXLuno0aOG\n3lzh5uamcuXKqXTp0uzNjUyBZjcAAGnAyclJ7733noKCgtS7d2/D9ty+efOmunfvrpo1a2r37t2G\n5AQAAAAAAE+WPXt2+fr6WsT3799vV97AwECLWP78+eXj4/PY45ycnOw676PCw8MtYoULF7a5OXb8\n+HFFR0fbW1a6KFq0qLy8vCzi1n5W+D/+/v4WsXPnzlm9tpIrNjZWhw8fTta5HJXZbNaNGzd09OhR\nhYaGGrY3t7Ozs4oWLaqKFSuy5QgyFZrdAACkIQ8PD3399df6+++/9eyzzxqW9++//1bdunX14Ycf\nclcxAAAAAABppHLlyhaxP/74Q3FxcTbn/PXXXy1iyWnkWVtlbk8d1vZFzpkzp835fv75Z5uPzQis\nbVG3efPmdKjEcfj7+1vchJGQkKDff//d5pzbtm2zuve7tfeiI4qKitKpU6cYWQ6kAFc0AADpwN/f\nX1u3btWiRYtUqFAhw/LOmzdPvr6+CggIYLQ5AAAAAACprHHjxhaxmzdvWm1YJ8eePXusjvpu0qTJ\nE491d3e3iN27d8+mOiQpV65cFrGrV6/alOvq1atav369zbVkBC+//LJFbMuWLTp16lQ6VOMYcufO\nrVq1alnEV65cqdjY2BTnM5vNWrJkiUW8ZMmSKl26tE01ZhQPjyy31sy3FSPLkRXQ7AYAIJ04OTmp\nbdu2CgoK0qeffmroaPMePXqoRo0a2rVrlyE5AQAAAACApSpVqqh8+fIW8YCAAKsrox8nNjZW48eP\nt4gXKFDAalP9Ublz57aIPbrndkrkz5/far6zZ8+mKI/ZbNaXX37psCPM76tRo4bFz9psNmvYsGF2\n3VSQ2b399tsWsfPnz2vx4sUpzrVu3TodOnTIIt66dWvDx/inFUaWA/aj2Q0AQDrLkyePJk2apIMH\nD6pBgwaG5T148KDq1aunDz74gNHmAAAAAACkkjZt2ljEwsPD1b9//2SPIU5ISNDgwYP177//WjzW\nunVrubi4PDFHqVKlLGJnzpxJcdP9Pg8PD6s5p0+fnuwcZrNZEydO1O7du22qIaP59NNPLZqqQUFB\n6t+/v+7cuWN3/v3792vv3r1258lI6tevr+LFi1vEZ8yYoR07diQ7z+HDhzV27FiLuIeHh9VV944g\ntUaW582bl5HlyFK4ygEAyCD8/Py0ZcsWLV68WD4+PoblnT9/vsqVK6epU6fatVcXAAAAAACw1Lx5\nc9WuXdsivm/fPvXs2fOJq6uvX7+u/v37a+PGjRaPlStXTu+9916y6sidO7eKFCmSKBYXF6f58+cn\n63hrGjVqZBHbvHmzxo0b98TPGK5du6bPP/9cP/zww4OYUVPt0kv16tX1zjvvWMT37NmjNm3aaOvW\nrSlemXv16lWtXLlSbdu2VdeuXXX8+HGjys0QnJ2dNWTIEIuma1xcnAYMGKDVq1c/8Xu2YcMG9erV\ny+oK+oEDB9q1l3x6iI+P18WLF1NtZHmpUqUYWY4s5cm3gwEAgDTj5OSkNm3aqEWLFho+fLi++eYb\nQ/bevnXrlnr27Km5c+cqICBA9erVM6BaAAAAAADg5OSkYcOG6e2339atW7cSPRYYGKi3335bzZs3\nV5MmTVSiRAl5eXnp1q1bunjxojZv3qy1a9daHCdJrq6uGjlypLJly5bsWho3bqwFCxYkis2fP1+H\nDx/Wc889p+LFi8vd3d1q09nf398i1qZNGy1btkx3795NFF++fLn++usvvfnmm6pZs6YKFy4sFxcX\nhYeH69y5c9q6dat+/fXXRMeVKFFC5cqV0x9//JHs15MR9erVS//++6/F1nGhoaHq27evihUrpiZN\nmqhKlSoqWbKkPDw8lCNHDt27d08RERG6ceOGTp8+rVOnTungwYM6duyYYaOrM6qqVauqffv2mjdv\nXqJ4dHS0Ro8erZ9++kktWrRQrVq1lD9/fplMJl29elUHDx7UunXrtH//fqt5X3rpJb3wwgtp8RIM\nYTabdfPmTV24cMHQldzOzs4qXLiwChYsyEpuZEk0uwEAyIDy5MmjiRMn6sMPP1SPHj20ZcsWQ/Ie\nOnRI9evX1/vvv69x48bJ29vbkLwAAAAAAGRl+fPn18SJE9WzZ09FRkYmeiwyMlKrVq3SqlWrkp3P\nxcVFo0aNsjpG/HHeeOMNLVu2zGJ/7AMHDujAgQOPPTYwMNAi5unpqU8//VQjR460eOzcuXOaMGFC\nsurKkyePxo0bp4ULFybr+RmZi4uLxo0bpy+++EJbt261ePzChQsWTV1IH330kc6fP69NmzZZPHbs\n2DEdO3YsRfmqVaumQYMGGVVeqouKitL58+cNXckt/TeyvGjRoqzkRpbGLR4AAGRglSpV0p9//qml\nS5caOtp8wYIFKleunKZMmcJocwAAAAAADFC1alXNmjXL7v9/9/T01NSpU62OEH+SokWLqk+fPnad\n/1GvvfaaOnbsaPPx+fLl09SpU1W6dGkDq0pfbm5uGj9+vHr06JGilffJkZz92R2RyWTSqFGj9O67\n79qdq3nz5poyZYrc3NwMqCx1pdbI8hw5csjX15eR5YBodgMAkOE5OTnpnXfeUVBQkPr162fY//Tc\nvn1bvXr1UvXq1bVjxw5DcgIAAAAAkJWVL19eP/zwg9q0aSNXV9cUHWsymfTKK69oxYoVqlmzps01\ntGrVShMmTFDBggVtzvGobt26adSoUfLw8EjRcc8//7wWLVqkSpUqGVZLRuHs7KwOHTpoxYoVat68\nuV1N71y5cqlly5aaMWOG2rZta2CVGYuLi4v69u2rb7/9VuXKlUvx8cWLF9e4ceM0YsSIDN/oNpvN\nun79uo4eParLly8bNqre2dlZRYsWVYUKFZQ7d25DcgKOzsmc2TeDyACqV6+uy5cvq1ChQknuLQEA\nQHIdO3ZMPXr00ObNmw3Ny2hzAAAAIOs6deqU4uLi5OLiorJly6Z3OUC6OHPmjMXe1O7u7ikeJX7f\njRs39Ntvv2n79u06evSoRW7pv325K1asqHr16unFF19UoUKFbDqXNfHx8dq9e7f27t2rkydP6tKl\nS7p7964iIyMVHx9v8XxrY8wfde/ePf3444/asmWLjhw5YrHvsMlkUokSJVS7dm298sr/Y+++w2u+\n//+PP5IQQew9G1pZEnvVrJZSRfmUqr1XY+8t9qhd1CpqlKo9SlF7lyDIorRmqBUzSHJ+f/RX36aJ\nkeSVfb9dl+tqXue8H+d1nCTSPM/78a6r9957L9ztx44d06VLl8KtlS1bVg4ODlF/ggnM3bt3tWvX\nLh0+fFi+vr66detWpPezsbFR7ty55eDgIDc3N5UpU0aurq6RXkc9qTt+/Li2b9+u48eP68qVK5EO\nhHPnzq3ixYurevXqKl++fKK4JvXTp0915coVKsuRaCT2nwMZdscBht0AANMsFotWrVqlXr166fr1\n68Zy06dPr5EjR8rDwyPJ1mYBAAAAiCix/5ITSAxu376te/fu6fnz50qZMqUyZsyobNmyycrKKr63\nFi0vXrzQnTt3FBQUJIvFInt7e+XIkcN4rXdiFRwcrFu3bunJkycKCwtTmjRplDZtWmXMmJG/o0g8\ne/ZMN2/efPmmkNSpUytHjhxKnTp1PO/s7YWGhurGjRu6efOmsTO5pb//LvLnz8+Z3Ig1if3nQIbd\ncYBhNwAgtjx8+FCjRo3S1KlTjV57293dXbNmzVKlSpWMZQIAAABIuBL7LzkBAIgvFotF9+7d09Wr\nVyO0HcSEtbW18uTJo2zZsiWKM9qReCX2nwP56gAAIBFLly6dJk6cqNOnT+vDDz80lnvmzBlVrlxZ\nzZs3V2BgoLFcAAAAAAAAIKl4+vSpzp8/r4sXLxoddGfOnFlubm7KkSMHg27gDfgKAQAgCXB1ddXO\nnTu1cuVK5cmTx1jusmXL5OTkpGnTphk9cxwAAAAAAABIrEJDQ3X16lX5+PgYvTZ36tSp5eTkpIIF\nC3JtbuAtMewGACCJsLKyUqNGjeTn56d+/foZu+b2gwcP1LNnTxUvXlz79u0zkgkAAAAAAAAkNhaL\nRXfv3tXZs2cVGBho7Nrc1tbWypcvn1xcXLg2NxBFDLsBAEhi7O3tNWHCBHl7e+ujjz4ylnv27FlV\nqVJFzZo1040bN4zlAgAAAAAAAAnd06dPFRAQoIsXL+rFixfGcqksB2KGrxoAAJIoFxcX7dixQ6tW\nrTJabb58+XI5OTlp6tSpRn+wBwAAAAAAABKaf1eWP3z40FguleWAGQy7AQBIwqysrNSwYUP5+fmp\nf//+SpkypZHchw8fqlevXipevLj27t1rJBMAAAAAAABIKGKrstzGxkb58uWTq6srleWAAQy7AQBI\nBuzt7TV+/Hh5e3urWrVqxnLPnTunDz74QE2bNtX169eN5QIAAAAAAADxJbYqy7NkyfKystzKyspY\nLpCcMewGACAZcXZ21vbt2/XTTz8pb968xnJ/+OEHOTk5afLkyVSbAwAAAAAAIFEKDQ3VlStXYq2y\nvECBAsaaFwH8jWE3AADJjJWVlRo0aCA/Pz8NGDDA2A/Yjx49Up8+fVSsWDHt2bPHSCYAAAAAAAAQ\n2/5dWX7z5k0qy4FEhGE3AADJVNq0aTVu3DidOXNG1atXN5br4+OjqlWrqkmTJlSbAwAAAAAAIEGj\nshxI3Bh2AwCQzDk5OemXX37R6tWrlS9fPmO5K1askJOTkyZNmkS1OQAAAAAAABKU2Kwsd3Z2prIc\niCMMuwEAgKysrPT555/L19dXgwYNMlpt3rdvXxUrVky7d+82kgkAAAAAAABEl8Vi0Z07d2K1stze\n3t5IJoA3Y9gNAABeSps2rcaMGaOzZ8/q448/Npbr4+OjDz/8UI0bN9a1a9eM5QIAAAAAAABv65/K\n8kuXLlFZDiQRDLsBAEAEjo6O2rZtm9asWaP8+fMby125cqWcnZ319ddf6/nz58ZyAQAAAAAAgFeJ\nrcryNGnSUFkOxDOG3QAAIFJWVlb63//+J19fXw0ePFi2trZGch89eqR+/fqpaNGi+vXXX41kAgAA\nAAAAAP8Vm5Xl+fPnl4uLC5XlQDxj2A0AAF4rTZo0Gj16tM6ePasaNWoYy/Xz81O1atXUqFEjXb16\n1VguAAAAAAAAENuV5dmzZ6eyHEgAGHYDAIC3UqhQIW3dulVr1641Wm2+atUqOTs7a+LEiVSbAwAA\nAAAAIEb+qSw/d+4cleVAMsCwGwAAvDUrKyvVr1/feLX548eP1b9/f6rNAQAAAAAAEC3/rSw3hcpy\nIGFj2A0AAKLs39Xmn3zyibHcf6rNv/jiC6rNAQAAAAAA8FaePn0qf39/45XlWbNmpbIcSOAYdgMA\ngGgrVKiQtmzZovXr1+udd94xlvvTTz/J2dlZEyZMoNocAAAAAAAAkfp3ZfmjR4+M5f5TWe7g4EBl\nOZDAMewGAAAxYmVlpc8++0w+Pj4aOnSoUqVKZST38ePHGjBggIoUKaIdO3YYyQQAAAAAAEDiR2U5\ngH8w7AYAAEakSZNGI0eO1NmzZ1WrVi1juf7+/vr444/VsGFDXblyxVguAAAAgP9jY2Mj6e8z5AAA\nSMiePHlCZTlg0D8///3z82Biw7AbAAAY9d5772nz5s3asGGDHBwcjOWuXr1azs7OGj9+PNXmAAAA\ngGHW1n//mtBisSgsLCyedwMAQEQhISG6cuWKfHx8qCwHDAkLC5PFYpHEsBsAAOAlKysr1a1bVz4+\nPho2bJixavMnT55o4MCBcnd31/bt241kAgAAAFC4X+4/efIkHncCAEB4/1SWnzt3jspywLB//9yX\nWN/swbAbAADEmtSpU2vEiBE6d+6cPv30U2O5AQEBqlGjhho0aKDLly8bywUAAACSq3Tp0r3874cP\nH8bjTgAA+D9UlgOx68GDBy//O7G+6YNhNwAAiHXvvvuuNm/erI0bNxqtNl+zZo1cXFw0btw4PXv2\nzFguAAAAkNzY29u/rDJ/+PDhyzpLAADiQ0hIiC5fvkxlORCLLBbLy68va2trht0AAABvUqdOHfn4\n+Gj48OFGq80HDRokd3d3/fLLL0YyAQAAgOTm37/gDA0NVVBQUDzvCACQHFksFt2+fVvnzp3TrVu3\njOVSWQ5EFBQUpNDQUEnh3/iY2CTOXQMAgEQrderU8vT0lI+Pj+rUqWMs9/z586pZs6Y+//xzqs0B\nAACAaPh3lfmNGzfC1VoCABDb/qks/+OPP6gsB2LZgwcPdOPGjZcf//vnwMSGYTcAAIgXBQsW1MaN\nG7Vp0yYVKFDAWO7atWvl7OyssWPHUm0OAAAAREG6dOmUIUOGlx9fu3ZN9+/fp9IcABCrYrOy3MXF\nhcpy4F8sFovu37+va9euvVzLkCFDoh52W1n4aTXWlSxZUoGBgcqZM6dOnDgR39sBACDBefr0qSZO\nnKjx48crODjYWG6hQoU0Y8YM1axZ01gmAAAAkJRZLBbduHEjXI25jY2N7O3tlT59eqVJkybRVlwC\nABIWi8WiO3fu6OrVqwoJCTGWmyJFCuXJk0dZs2blTG5AUlhYmJ48eaIHDx7o0aNHL6vLpb8H3bly\n5UrUXysMu+MAw24AAN7OpUuX1KNHD23cuNFobr169TR16lQ5ODgYzQUAAACSosgG3v9mZWUlGxub\nON4VACApCQ0NVXBwsNEhtyTZ2trKzs4uUQ/uAJNCQ0Nf2dKTFAbdEsPuOMGwGwCAqNmyZYu6deum\nixcvGstMnTq1Bg0apD59+sjOzs5YLgAAAJAUWSwWPXz4UA8fPtSjR48UFhYW31sCACQBYWFhun//\nvh4+fGg019bWVpkzZ1aqVKmM5gJJjbW1tezt7ZUuXTqlS5cu0Q+6JYbdcYJhNwAAURccHKyJEydq\n3LhxRqvN33vvPc2YMUOffPKJsUwAAAAgKQsLC9OjR4/06NEjvXjxQqGhoeHqLwEAeBvXrl2Tn5+f\nnj9/biwzZcqUcnJyUt68eZPE0A4wzcbGRjY2NkqZMqXs7e1lb2+f5C5Jw7A7DjDsBgAg+i5duqSe\nPXtqw4YNRnM/++wzTZs2jWpzAAAAAACAWHTq1Cl5eHjo0KFDxjKtrKzUvn17jR07VlmyZDGWCyDx\nSVqjewAAkOQUKFBA69ev15YtW/Tuu+8ay92wYYNcXFw0atQoo2eOAwAAAAAAQLp//766du2qkiVL\nGh10ly5dWkePHtXcuXMZdANg2A0AABKHWrVq6ezZsxo1apSxa24HBwdr2LBhcnNz05YtW4xkAgAA\nAAAAJGdhYWFatGiRHB0dNXPmTIWFhRnJzZw5s+bNm6cjR46odOnSRjIBJH4MuwEAQKJhZ2enIUOG\nyNfXV/Xq1TOW+/vvv6t27dr67LPPdOnSJWO5AAAAAAAAycnJkydVsWJFtWnTRn/99ZeRTCsrK3Xs\n2FEBAQFq3759krveMICY4TsCAABIdBwcHLRu3Tr9/PPPeu+994zlbty4Ua6urho5ciTV5gAAAAAA\nAG/p3r176tKli0qVKqXDhw8byy1TpoyOHTumOXPmUFkOIFIMuwEAQKL1ySef6MyZMxo9erRSp05t\nJDM4OFjDhw9X4cKFqTYHAAAAAAB4jbCwMC1cuFBOTk6aNWuWscryLFmyaP78+Tp8+LBKlSplJBNA\n0sSwGwAAJGp2dnYaPHiwfH19Vb9+fWO5Fy9eVO3atVW3bl1dvHjRWC4AAAAAAEBS4OXlpQoVKqht\n27ZGK8s7deqkgIAAtWvXjspyAG/EdwkAAJAkvPPOO1q7dq22bt1qtNp806ZNcnV11YgRI/T06VNj\nuQAAAAAAAInRvXv35OHhoVKlSunIkSPGcv+pLP/222+VOXNmY7kAkjaG3QAAIEmpWbOmzp49qzFj\nxhirNn/27Jk8PT1VuHBhbd682UgmAAAAAABAYvJPZbmjo6Nmz54ti8ViJDdr1qxasGABleUAooVh\nNwAASHJSpUqlQYMGydfXV//73/+M5V66dEl16tRRnTp1qDYHAAAAAADJhpeXl8qXL6+2bdvq9u3b\nRjKtrKzUuXNn+fv7q23btlSWA4gWvnMAAIAk65133tGaNWv0yy+/yNHR0Vju5s2b5erqKk9PT6rN\nAQAAAABAknX37l199dVXKlWqlI4ePWost2zZsvrtt980e/ZsKssBxAjDbgAAkOR9/PHH8vb21tix\nY5UmTRojmc+ePdOIESNUuHBhbdq0yUgmAAAAAABAQhAWFqYFCxbI0dFR3377rdHK8u+++06HDh1S\nyZIljWQCSN4YdgMAgGQhVapUGjhwoHx9ffX5558by7106ZLq1q2r2rVr6/fffzeWCwAAAAAAEB9O\nnDih8uXLq3379rpz546RTGtra3311Vfy9/dXmzZtqCwHYAzfTQAAQLKSP39+rV69Wtu3bzdabb5l\nyxYVLlxYw4YN05MnT4zlAgAAAAAAxIW7d++qc+fOKl26tNHK8vfff1/Hjx/XrFmzqCwHYBzDbgAA\nkCxVr15d3t7eGjdunNFq81GjRqlw4cLasGGDsYovAAAAAACA2PLvyvI5c+YY+31GtmzZtHDhQh04\ncEDFixc3kgkA/8WwGwAAJFupUqXSgAED5Ofnp4YNGxrL/eOPP1SvXj19+umnunDhgrFcAAAAAAAA\nk44fP67333/feGW5h4eH/P391bp1ayrLAcQqvsMAAIBkL1++fFq1apV27NghJycnY7lbt25V4cKF\nNXToUKrNAQAAAABAgnHnzh116tRJZcqU0bFjx4zl/lNZPnPmTGXKlMlYLgC8CsNuAACA/69atWry\n9vbWhAkTlDZtWiOZz58/1+jRo+Xq6qr169dTbQ4AAAAAAOJNWFiY5s+fL0dHR82dO9doZfmiRYuo\nLAcQ5xh2AwAA/Iutra369esnPz8/ffHFF8Zy//zzT9WvX1+1atXS+fPnjeUCAAAAAAC8jd9++03l\nypVThw4ddPfuXSOZ1tbW6tKliwICAtSqVSsqywHEOb7rAAAARCJv3rz68ccftXPnTjk7OxvL3bZt\nm9zc3DRkyBCqzQEAAAAAQKy7c+eOOnbsqLJly+q3334zllu+fHmdOHFC33zzjTJmzGgsFwCigmE3\nAADAa3z00Uc6ffq0Jk6caLTafMyYMXJxcdG6deuoNgcAAAAAAMaFhoZq7ty5cnR01Lx584xWli9e\nvFj79+9XsWLFjGQCQHQx7AYAAHgDW1tb9e3bV35+fmrUqJGx3MuXL+t///ufPvnkEwUEBBjLBQAA\nAAAAyduxY8dUrlw5derUyWhledeuXRUQEKCWLVtSWQ4gQeA7EQAAwFvKmzevVq5cqZ07d8rFxcVY\n7i+//CJ3d3cNHjxYjx8/NpYLAAAAAACSl9u3b6tDhw4qV66cjh8/biy3QoUKOnHihGbMmEFlOYAE\nhWE3AABAFH300Uc6deqUvv76a6PV5mPHjpWLi4vWrl1LtTkAAAAAAHhr/1SWOzk5af78+cZ+r5A9\ne3Z9//33VJYDSLAYdgMAAESDra2t+vTpI39/f3355ZfGcq9cuaLPP/9cNWvWpNocAAAAAAC80dGj\nR1W2bFnjleXdunWTv7+/WrRoISsrKyO5AGAaw24AAIAYyJMnj1asWKFdu3bJ1dXVWO727dvl5uam\nQYMGUW0OAAAAAAAiuH37ttq3b69y5crpxIkTxnIrVqwoLy8vTZ8+ncpyAAkew24AAAADqlatqlOn\nTmnSpEmyt7c3kvnixQuNGzdOLi4uWrNmDdXmAAAAAABAoaGhmjNnjhwdHbVgwQJjuTly5NCSJUu0\nb98+FS1a1FguAMQmht0AAACGpEyZUr1795a/v78aN25sLPfKlStq0KCBatSoIX9/f2O5AAAAAAAg\ncTl69KjKlCmjzp076969e0YybWxs1L17d/n7+6t58+ZUlgNIVBh2AwAAGJY7d2798MMP2r17twoX\nLmwsd8eOHXJ3d9eAAQP06NEjY7kAAAAAACBh++uvv9SuXTuVK1dOXl5exnL/qSyfNm2aMmTIYCwX\nAOIKw24AAIBY8sEHH+jkyZOaPHmy0qVLZyTzxYsXmjBhglxcXPTTTz9RbQ4AAAAAQBIWGhqq2bNn\ny8nJSd99952x3Bw5cmjp0qXat2+fihQpYiwXAOIaw24AAIBYlDJlSvXq1Ut+fn5q0qSJsdyrV6/q\niy++0Mcffyw/Pz9juQAAAAAAIGE4cuSIypQpIw8PD6OV5T169JC/v7+aNWtGZTmARI9hNwAAQBzI\nnTu3li9frj179sjNzc1Y7s6dO1WkSBH179+fanMAAAAAAJKAv/76S23bttX7779vtLK8UqVKOnny\npKZOnUplOYAkg2E3AABAHKpSpYq8vLw0depUo9XmEydOlLOzs1atWkW1OQAAAAAAidA/leWOjo5a\nuHChsdycOXNq2bJl2rt3r9zd3Y3lAkBCwLAbAAAgjqVMmTJcZZgp165dU6NGjVS9enX5+voaywUA\nAAAAALHr8OHDKl26tDw8PHT//n0jmTY2NurZs6f8/f3VtGlTKssBJEkMuwEAAOJJrly5tHTpUuPv\nrP71119VpEgR9evXTw8fPjSWCwAAAAAAzLp165batGmj8uXL6+TJk8ZyK1eurFOnTmnKlClKnz69\nsVwASGgYdgMAAMSzypUry8vLS9OmTTP2P6AhISH6+uuv5ezsrB9//JFqcwAAAAAAEpDQ0FDNmjVL\nTk5OWrRokbHcXLlyafny5dqzZ4/c3NyM5QJAQsWwGwAAIAFIkSKFunfvLn9/fzVv3txY7vXr1/Xl\nl1+qWrVq8vHxMZYLAAAAAACi59ChQypVqpS6dOlitLK8V69e8vPzU5MmTagsB5BsMOwGAABIQHLm\nzKklS5Zo3759RqvNd+3apaJFi6pv375UmwMAAAAAEA9u3bql1q1bq0KFCjp16pSx3CpVqujUqVOa\nPHkyleUAkh2G3QAAAAlQpUqV5OXlpenTpxutNp80aZKcnZ21cuVKqs0BAAAAAIgDISEh+uabb+To\n6KjFixcby82VK5d++OEH7d69m8pyAMkWw24AAIAEKkWKFOrWrZv8/f3VokULY7nXr19X48aN9dFH\nH+ncuXPGcgEAAAAAQHgHDx5UqVKl1K1bNwUFBRnJtLGxUe/eveXn56fGjRtTWQ4gWWPYDQAAkMDl\nzJlT33//vfbv368iRYoYy929e7eKFSumPn36UG0OAAAAAIBBN2/eVKtWrVSxYkWdPn3aWO4HH3yg\n06dPa9KkSVSWA4AYdgMAACQaFStW1IkTJzRjxgyj1eaTJ0+Wk5OTVqxYQbU5AAAAAAAx8E9luZOT\nk77//ntjublz59aKFSu0a9cuFS5c2FguACR2DLsBAAASkRQpUqhr164KCAhQy5YtjeXeuHFDTZo0\nUdWqVak2BwAAAAAgGg4cOKCSJUsarSxPkSKF+vTpIz8/P3355ZdUlgPAfzDsBgAASIRy5MihxYsX\n68CBAypatKix3L1796po0aLq3bu3Hjx4YCwXAAAAAICk6ubNm2rZsqUqVaokb29vY7lVq1bV6dOn\n9fXXXytdunTGcgEgKWHYDQAAkIhVqFBBx48f1zfffKMMGTIYyQwNDdWUKVPk7Oys5cuXU20OAAAA\nAEAkQkJCNGPGDDk6OmrJkiXGcnPnzq2VK1fq119/laurq7FcAEiKGHYDAAAkcilSpFCXLl0UEBCg\nVq1aGcu9ceOGmjVrpg8++EBnz541lgsAAAAAQGK3f/9+lSxZUt27dzfWjJYiRQr17dtXfn5+atSo\nEZXlAPAWGHYDAAAkEdmzZ9eiRYt08OBBFStWzFjuvn37VKxYMfXq1YtqcwAAAABAshYYGKgWLVqo\ncuXKRivLP/zwQ3l7e2vixIlUlgNAFDDsBgAASGLKly+v48ePa+bMmcqYMaORzNDQUE2dOlVOTk5a\ntmwZ1eYAAAAAgGQlJCRE06ZNk5OTk5YuXWosN0+ePPrxxx+1c+dOubi4GMsFgOSCYTcAAEASZGNj\nIw8PD/n7+6tNmzbGcgMDA9W8eXNVqVJFZ86cMZYLAAAAAEBCtW/fPpUoUUI9e/Y0Wlner18/+fn5\n6YsvvqCyHACiiWE3AABAEpY9e3Z99913OnTokIoXL24sd//+/SpevLh69uypoKAgY7kAAAAAACQU\nN27ciJU3fH/00Ufy9vbWhAkTZG9vbywXAJIjht0AAADJwPvvv6/ffvtNs2bNMlpt/u8KN6rNAQAA\nAABJwb8ry5ctW2YsN2/evFq1apV27NhBZTkAGMKwGwAAIJmwsbHRV199pYCAALVt29ZY7s2bN9Wi\nRQtVrlxZ3t7exnIBAAAAAIhr+/bte9lk9vDhQyOZKVOmVP/+/eXr66uGDRtSWQ4ABjHsBgAASGay\nZcumBQsW6PDhwypRooSx3AMHDqhEiRLq3r071eYAAAAAgETlxo0batasmapUqaKzZ88ay61WrZq8\nvb01fvx4KssBIBYw7AYAAEimypUrp2PHjmn27NnKlCmTkczQ0FDNmDFDTk5OWrJkCdXmAAAAAIAE\n7cWLF5o6daqcnJy0fPlyY7l58+bVTz/9pO3bt8vZ2dlYLgAgPIbdAAAAyZiNjY06d+6sgIAAtWvX\nzljuzZs31bJlS1WqVEmnT582lgsAAAAAgCl79+5V8eLF1atXL6OV5QMGDJCvr68aNGhAZTkAxDKG\n3QAAAFDWrFk1f/58HTlyRCVLljSWe/DgQZUoUULdunXT/fv3jeUCAAAAABBd169fV9OmTfXBBx/o\n3LlzxnKrV6+uM2fOaNy4cVSWA0AcYdgNAACAl8qWLaujR49qzpw5xqrNw8LC9M0338jJyUnff/+9\nwsLCjOQCAAAAABAVL1680JQpU+Tk5KQffvjBWG6+fPm0evVq/fLLL3JycjKWCwB4M4bdAAAACMfG\nxkYdO3ZUQECA2rdvb6xy7datW2rVqpUqVaqkU6dOGckEAAAAAOBt7NmzR8WLF1fv3r316NEjI5kp\nU6bUwIED5evrq88//5zKcgCIBwy7AQAAEKmsWbNq3rx5OnLkiEqVKmUs99ChQypZsqS6du1KtTkA\nAAAAIFZdv35dTZo0UdWqVY1Wln/88cc6c+aMxo4dq7Rp0xrLBQBEDcNuAAAAvFaZMmV05MgRzZ07\nV5kzZzaSGRYWppkzZ8rR0VGLFi2i2hwAAAAAYNSLFy80efJkOTk5acWKFcZy8+fPrzVr1mjbtm1U\nlgNAAsCwGwAAAG9kY2OjDh06KCAgQB06dDBWzfbXX3+pTZs2qlixok6ePGkkEwAAAACQvO3evVvF\nihVTnz59jFWW29raatCgQfLx8dH//vc/KssBIIFg2A0AAIC3liVLFs2dO1dHjx5V6dKljeUePnxY\npUqVUpcuXXTv3j1juQAAAACA5OPatWtq3LixPvzwQ/n4+BjLrVGjhs6cOaMxY8ZQWQ4ACQzDbgAA\nAERZ6dKldeTIEc2bN89otfmsWbPk5OREtTkAAAAA4K29ePFCkyZNkrOzs1auXGksN3/+/Fq7dq22\nbt0qR0dHY7kAAHMYdgMAACBarK2t1b59ewUEBKhjx47Gq80rVKggLy8vI5kAAAAAgKRp165dKlq0\nqPr27Wu0snzw4MHy9fVV/fr1qSwHgASMYTcAAABiJEuWLJozZ46OHTumMmXKGMs9cuSISpUqJQ8P\nD6rNAQAAAADhXLt2TV9++aU++ugj+fr6GsutWbOmzp49q9GjRytNmjTGcgEAscPKYrFY4nsTSV3J\nkiUVGBionDlz6sSJE/G9HQAAgFgTFhamhQsXasCAAbpz546x3KxZs2rChAlq1aqVrK15vyYAAG9j\n06ZNGjFiRLi12rVry9PTM342hDhnsVh05MgRHTp0SGfPntXNmzf18OFDPX36NNz97O3ttWfPnvjZ\nJABE0fPnzzV9+nSNGDFCjx8/NpabP39+TZ8+XZ999hlncgNAIsJvCgEAAGCMtbW12rVrp4CAAHXq\n1MnYLwhu376ttm3bqnz58rx5EAAA4C2cPHlSDRo0UNeuXbVixQqdOXNGt27dijDoBoDE5Ndff1XR\nokXVr18/Y4NuW1tbDRkyRL6+vqpXrx6DbgBIZFLE9wYAAACQ9GTOnFnffvut2rVrJw8PDx09etRI\n7tGjR1W6dGl17NhRY8aMUebMmY3kAgCSnrlz52r+/PlROsbOzk729vayt7dX7ty5VbhwYbm6uqpM\nmTJKlSpVLO0UMG/btm0aPny4QkND43srAGDE1atX1bt3b61atcpo7ieffKLp06erUKFCRnMBAHGH\nYTcAAABiTcmSJXXo0CEtWrRIAwYM0O3bt2OcabFYNGfOHP30008aP3682rRpQ7U5AMCI4OBgBQcH\n6/bt2/rjjz906NAhSVKGDBn06aefqkmTJsqZM2c87zJ5OnHihJ49exZurUSJErKzs4unHSVcly5d\n0qhRoxh0A0gSnj9/rmnTpmnkyJFGK8vfeecdTZ8+XXXr1uVMbgBI5Bh2AwAAIFZZW1urbdu2ql+/\nvoYOHapvv/1WFoslxrl37txR+/btNX/+fM2aNUulSpUysFsAACIKCgrSDz/8oA0bNqhPnz6qU6dO\nfG8p2fH09NSNGzfCrW3cuFG5c+eOpx0lXAsXLozwxgBra2t99NFHqlChgnLkyBHhTQI2NjZxuUUA\neCs7d+5U165d5efnZywzVapU6tevnwYMGKA0adIYywUAxB+G3QAAAIgTmTNn1qxZs9S2bVt5eHjo\nyJEjRnKPHTumMmXKqEOHDhozZoyyZMliJBcAgP96/PixRowYoT///FNdunSJ7+0AETx69Eg7duyI\nsD527FhVq1YtHnYEAFF39epV9erVSz/99JPR3Fq1amn69Ol67733jOYCAOIXw24AAADEqRIlSujg\nwYP6/vvv1a9fP2PV5nPnztXq1as1btw4tW3blmpzAECkFi1a9Mrbnjx5ovv378vPz08HDhzQpUuX\nIr3f4sWLlSNHDjVs2DC2tmlEnTp1OAs9mTl79qxCQkLCrRUpUoRBN4BE4fnz55o6dapGjRpltLLc\nwcFB06dPV506dagsB4AkiN8AAgAAIM5ZW1urdevWCggIkIeHh7HB9J07d9ShQweVK1dOv/32m5FM\nAEDS4u7u/so/ZcuWVY0aNdS9e3etWrVKEydOVMaMGSPNmTFjhpE3bAEmRVb1W7JkyXjYCQBEzY4d\nO1SkSBENGDDA2KA7VapUGjZsmHx8fLg2NwAkYQy7AQAAEG8yZcqkmTNn6vjx43r//feN5f72228q\nW7asOnbsqDt37hjLBQAkH1ZWVvrwww+1dOnSSC+R8fTpU3333XfxsDPg1YKCgiKs5ciRIx52AgBv\n58qVK2rYsKE+/vhj+fv7G8v99NNPde7cOY0YMUKpU6c2lgsASHgYdgMAACDeFS9eXAcOHNCiRYuU\nLVs2I5kWi0Xz5s2To6Oj5s2bp9DQUCO5AIDkJVeuXBo1alSkt23fvl1hYWFxvCPg1R49ehRhLVWq\nVPGwEwB4vefPn2v8+PFydnbW6tWrjeU6ODho48aN2rx5s959911juQCAhIthNwAAABIEa2trtWrV\nSv7+/urSpYuxavO7d++qY8eOKleunI4dO2YkEwCQvJQpU0bFixePsB4UFBRpbTQQX168eBHfWwCA\nN9q+fbvc3d01cOBAPXnyxEhmqlSpNHz4cPn4+KhOnTpGMgEAiUOK+N4AAAAA8G+ZMmXSN998o7Zt\n28rDw0OHDh0yknv8+HGVK1dO7dq109ixY5U1a1YjuQCA5KFKlSo6efJkhPWzZ8/K1dU1SllPnjyR\nr6+vrl69qqCgID1//lypUqVSpkyZlD9/fjk5OSW6s3Fv3bolX19f3bhxQ48fP1batGmVMWNGOTg4\nyMnJKVlfJzUpvt4AEB2XL19Wr169tGbNGqO5tWvX1rRp0ziTGwCSKYbdAAAASJCKFSum/fv3a+nS\nperbt6/++uuvGGdaLBbNnz9fa9as0dixY9WuXTvZ2NgY2C0AIKl71UD73r17b3X8ixcv9PPPP2vL\nli06ffr0ay+vkTJlSpUpU0afffaZqlatGu1B8aZNmzRixIhwa7Vr15anp+cbj71+/brq1q0bbi1X\nrlzatGnTy4/DwsK0detW/fjjj/Lx8XllVubMmVWjRg21bdtWGTNmfKu9z507V/Pnz3/tff67v1dp\n3769Onbs+Fb3NSUuXu/IXt/IjBgx4rX3e9vPCQCIrmfPnmnKlCkaPXq0sTO5JalAgQKaPn06Z3ID\nQDJHjTkAAAASLGtra7Vs2VIBAQHq2rWr0WrzTp06qWzZsjp69KiRTABA0pYpU6ZI1+/fv//GY/fv\n36/69etr1KhR8vLyeu3gU/p7UHrw4EH169dPTZo00dmzZ6Oz5Vj1559/qlWrVi8rY1/n7t27WrFi\nhT777DPt2rUrjnYYf5Li6w0A0fXLL7/I3d1dgwYNMjbotrOzk6enp86dO8egGwDAsBsAAAAJX8aM\nGTVjxgydOHFCFSpUMJZ74sQJlStXTu3bt9ft27eN5QIAkh6LxRKtY6ZPn66ePXsqMDAwWo97/vx5\ntW3bVj/99FO0jo8Np06dUuvWrd845P6vx48fa+DAgdqyZUss7Sx+JdXXGwCi4/Lly/r8889Vs2ZN\nnT9/3lhunTp1dO7cOQ0fPlypU6c2lgsASLwYdgMAACDR+Kfa/Pvvv1f27NmN5S5YsECOjo6aM2fO\nG8++AgAkT686g/t1tdwTJ07U0qVLX3m7vb29ChUqpFKlSqlgwYKv/KV9aGioJkyYoB9++CEqW44V\nFy5cUI8ePfTgwYNw6xkyZJCjo6NKly4tZ2dnpU2bNtLjQ0NDNXbsWF25ciUuthunkuLrDQBR9ezZ\nM40dO1bOzs5au3atsdyCBQtq06ZN2rhxowoWLGgsFwCQ+HHNbgAAACQqVlZWatGiherWravhw4dr\n5syZCgsLi3HuvXv31LlzZ82fP1+zZ89W2bJlDewWAJBUvOos5lcNu3/++edXnp1btmxZNWvWTKVL\nl1aKFP/3q5lnz57p4MGDWrhwofz8/CIcN336dBUuXFhFixaN+hMw4Pnz5+rfv78ePXokSUqRIoXq\n1aunevXqycnJKdy1pkNCQnTkyBHNmjUrwhl9z5490/jx4zVr1qxXPla9evVUvnz5lx/36dNHd+7c\nCXefr7/+WlmzZn3jvk2+Qe5V4uP1rlixohYtWhRubcGCBTp48GC4tbZt26pixYqv3PurKvoBIKq2\nbdumbt26GT2T287OTgMHDlS/fv1kZ2dnLBcAkHQw7AYAAECilDFjRk2fPl1t2rRRly5ddODAASO5\nXl5eKleunNq2batx48YpW7ZsRnIBAInb3r17I113c3OLsHbjxg1NnDgxwrq1tbX69eunBg0aRJqV\nKlUqffjhh6pcubJmz56tJUuWhLs9NDRUw4YN0w8//PDKM6dj0507d14OnHPmzKlp06bpvffei/S+\nKVKkUMWKFVWqVCn17t1bR48eDXf70aNH9eeff+qdd96J9PgcOXIoR44cLz+2tbWNcB8nJyflzp07\nuk/HmPh6vTNlyhRhUB3Z4Dpv3rxyd3ePylMCgCj5888/1bNnT61bt85obt26dTVt2jQVKFDAaC4A\nIGmhxhwAAACJWtGiRbVv3z4tWbIk3C/FY+q7776To6OjZs+eTbU5ACRzx44d08mTJyOsp0+fXi4u\nLhHW58yZ8/Ls53/r37//Kwef/5YiRQp169ZNTZo0iXDbtWvX4r3eOkuWLFq4cOErB93/ZmdnpzFj\nxihDhgwRbtu8eXNsbC/OJfXXGwBe5dmzZxozZoxcXFyMDroLFiyozZs3a8OGDQy6AQBvxLAbAAAA\niZ6VlZWaN28uf39/de/eXTY2NkZy79+/Lw8PD5UpU0ZHjhwxkgkASFxu3LihoUOHRnpb9erVZW0d\n/lcr9+7d044dOyLct0qVKvr888+j9NjdunWLdKC8Zs0ahYSERCnLpGHDhkWpGjxjxoyRPvfTp0+b\n3Fa8SA6vNwBEZtu2bXJzc9OQIUP09OlTI5l2dnYaOXKkzp07p08//dRIJgAg6WPYDQAAgCQjQ4YM\nmjZtmry8vFSpUiVjuV5eXnr//ffVpk0b3bp1y1guACDhslgs2r17t5o3bx7hWtHS3xXU7dq1i7C+\nfv16PX/+PNyajY2NevXqFeU9pEiRQr17946wfvv2be3atSvKeSa4u7urQoUKUT6uevXqEdb8/f1l\nsVhMbCveJPXXGwD+648//lD9+vX1ySef6MKFC8ZyP/vsM/n4+Gjo0KFcmxsAECVcsxsAAABJTpEi\nRbR371798MMP6tOnjwIDA43kLlq0SOvWrdPo0aPVqVMnY2eQAwDizpkzZ155W3BwsO7fvy8fHx8d\nOHBAly5deuV9PTw8lC1btgjrhw8fjrBWtmxZ5cmTJ1r7LV26tPLnz6/Lly9HeJyPP/44Wpkx8dln\nn0XruIIFCypVqlR69uzZy7XHjx/rzp07ypo1q6ntxbmk/noDwD+Cg4M1adIkjRkzRsHBwcZy3333\nXc2YMUO1atUylgkASF4YdgMAACBJsrKyUtOmTVWnTh15enpqxowZRq69ff/+fXXp0kXfffedZs2a\npffff9/AbgEAcaV169YxzmjcuHGk11cOCQmRj49PhPWYDilr1qypefPmhVt73dA+NhUrVixax9nY\n2ChXrlz6448/wq0/evQo0Q67k8PrDQCStHXrVnXt2lW///67sczUqVNr0KBB6tOnD2dyAwBihBpz\nAAAAJGnp06fXlClTdPLkSVWuXNlY7smTJ1W+fHm1bt2aanMASCZSp06tAQMGRFo1LUkXLlyI9Gw3\nNze3GD2uu7t7hLU///xTDx48iFFuVNnY2Oidd96J9vFp06aNsPbo0aOYbCleJfXXGwD++OMP1atX\nT7Vq1TI66K5Xr558fHw0ZMgQBt0AgBhj2A0AAIBkwd3dXXv27NHy5cuVM2dOY7mLFy+Wo6OjZs6c\nqZCQEGO5AICEw97eXg0bNtTKlSvVoEGDV94vsstm2NnZKX/+/DF6fCcnpwhrFotFN2/ejFFuVKVL\nl05WVlbRPj5VqlQR1v5da57YJPXXG0DyFRwcrFGjRsnFxUUbNmwwlvvee+/p559/1rp16+Tg4GAs\nFwCQvFFjDgAAgGTDyspKTZo0Ue3atTVixAhNnz7dSLV5UFCQunbtqgULFmjWrFmqUKGCgd0CAOJa\nqlSpZG9vL3t7e+XKlUsuLi4qXLiwypUr91ZnnkV25m2WLFlkbR2zcw0yZ84sGxubCP9mxfWZvqlT\npzaeabFYjGfGlaT+egNInrZs2aLu3bsbrywfPHiwevfuzZncAADjGHYDAAAg2UmfPr0mT56s1q1b\nq0uXLtq7d6+R3NOnT6tixYpq2bKlJkyYoBw5chjJBQCYc/z48VjLjmwYGVl1d3TY29srKCgo3NrD\nhw+NZCN6eL0BJCWXLl1Sjx49tHHjRqO59evX19SpU2N0GQwAAF6HGnMAAAAkW25ubtq9e7d++OEH\n5cqVy1ju999/LycnJ33zzTdUmwNAMhJZJXdk1d3REVnO06dPjWQjeni9ASQFwcHBGjlypFxdXY0O\nut977z1t3bpVa9euZdANAIhVDLsBAACQrFlZWalx48by8/NT7969ZWNjYyQ3KChI3bp1U8mSJXXg\nwAEjmQCAhC2ys3ofP35sJDuyHHt7eyPZiB5ebwCJ3ZYtW1S4cGENHz5cwcHBRjJTp06tMWPG6OzZ\ns6pZs6aRTAAAXodhNwAAAKC/q80nTZqk06dP64MPPjCW6+3trUqVKqlly5a6efOmsVwAQMKTPn36\nCGsmhp8Wi0VPnjx5q8dD3OH1BpBYXbx4UXXr1lXt2rV18eJFY7n/+9//5Ovrq0GDBhlrugAA4E0Y\ndgMAAAD/UrhwYe3atUsrVqxQ7ty5jeUuWbJEjo6OmjFjBtXmAJBERTaMvH37dqR111Fx7do1WSyW\nt3o8xB1ebwCJzdOnTzVixAi5urpq06ZNxnILFSqkbdu2ac2aNVSWAwDiHMNuAAAA4D+srKz05Zdf\nys/PT3369FGKFCmM5D548EDdu3dXyZIltX//fiOZAICEo0CBAhHWQkNDdeHChRjl+vn5RViztbVV\n3rx5Y5SLmOH1BpCYbN68WYULF5anp2eM35TzjzRp0mjs2LE6c+aMatSoYSQTAICoYtgNAAAAvEK6\ndOn09ddf6/Tp06pataqxXG9vb1WuXFktWrRQYGCgsVwAQPzKkyePsmTJEmHdy8srRrknTpyIsObs\n7KyUKVPGKDcxsbKyiu8tRMDrDSAxuHjxourUqaM6dero0qVLxnI///xz+fr6auDAgVSWAwDiFcNu\nAAAA4A1cXV3166+/auXKlUarzZcuXSonJydNmzaNanMASCKKFCkSYW3r1q3Rznvx4oW2b98eYd3d\n3T3amYlRZIPehPBvJ683gITq6dOn8vT0lKurqzZv3mws19HRUb/88otWr16t/PnzG8sFACC6GHYD\nAAAAb8HKykqNGjWSn5+f+vbta7TavGfPnipRooT27dtnJBMAEH8++uijCGsBAQE6fvx4tPI2b96s\noKCgCOvVqlWLVl5ilTZt2ghrT58+jYedhMfrDSAh2rRpkwoXLqwRI0YYrSwfN26cvL299fHHHxvJ\nBADABIbdAAAAQBSkS5dOEydOlLe3tz788ENjuWfOnFGVKlXUvHlz3bhxw1guACBuVatWLdJq66+/\n/jrKZyLfv39fM2fOjLDu6uqa7M70TZcuXYS1hPDvJa83gITk999/V+3atVW3bl2jleUNGjSQr6+v\nBgwYQGU5ACDBYdgNAAAARIOLi4t27typH3/8UXny5DGWu2zZMjk5OWnq1Kl68eKFsVwAQNxIkSKF\nGjZsGGH9999/14gRI2SxWN4qJzg4WH369In0LN8mTZrEeJ+JTcGCBSOseXt7x8NOwuP1BpAQPH36\nVMOHD1fhwoW1ZcsWY7lOTk7avn27fvrpJyrLAQAJFsNuAAAAIJqsrKz0xRdfyM/PT/379zdWbf7w\n4UP16tWLanMASKRatGih9957L8L61q1bNXDgQN2/f/+1x1+9elUeHh46depUhNsqVKigmjVrGtpp\n4uHs7BxhbePGjbp582Y87CY8Xm8A8cVisWjjxo1ydXXVyJEjjVaWjx8/Xt7e3qpevbqRTAAAYouZ\n38YBAAAAyZi9vb3Gjx+vVq1aqWvXrtq5c6eR3LNnz6pKlSpq2rSpvv76a+XKlctILgAgdtna2mr0\n6NFq0aKFnj9/Hu62nTt36vjx46pdu7aqVq2qPHnyKEOGDLp3757++OMP7dy5Uz///LOCg4Mj5GbK\nlEnDhg2Lq6eRoFSqVEmpUqUKN8i5f/++mjRpolq1aqlw4cLKmjVrpPW62bNnV44cOWJtb7zeAOLD\nhQsX1L17d/38889Gcxs2bKjJkycrX758RnMBAIgtDLsBAAAAQ5ydnbV9+3atXr1avXr10tWrV43k\nLl++XBs3bpSnp6e6du2qlClTGskFAMSe9957T6NGjdKgQYMUGhoa7rb79+9r2bJlWrZs2VvnpU2b\nVlOmTIn0+tDJQfr06VWrVi2tW7cu3HpQUJBWrFjx2mPbt2+vjh07xub2eL0BxJknT55o/PjxmjBh\nQoQ32MSEk5OTZs6cqWrVqhnLBAAgLlBjDgAAABhkZWWlhg0bytfXVwMGDDA2mH748KF69+6t4sWL\na8+ePUYyAQCx66OPPtL06dOVIUOGGOXkyZNH8+fPl7u7u6GdJU49evRI0NeM5fUGEJssFos2bNgg\nV1dXjRo1ytigO23atJowYYK8vb0ZdAMAEiWG3QAAAEAssLe317hx43TmzBmj17k7d+6cqlatqiZN\nmuj69evGcgEAsaNcuXJatWqV6tSpIxsbmygda2dnp+bNm2vFihVydHSMpR0mHmnTptXixYtVo0YN\nWVsnzF9p8XoDiA0XLlzQp59+qnr16unPP/80lvvFF1/Iz89P/fr1k62trbFcAADikpXFYrHE9yaS\nupIlSyowMFA5c+bUiRMn4ns7AAAAiGMWi0Vr1qxRr169dOXKFWO59vb28vT0VLdu3ag2B4D/uHnz\npm7duhVhPT7Plg0MDNTWrVt18OBB+fr6hrv+9D/Spk0rNzc3VapUSTVr1lTGjBnjfqOJwM2bN7Vj\nxw75+PjowoULun//vp48eRLpta/josY8MvHxei9btkxHjx4Nt9a0aVOVK1cuRrkA4seTJ080btw4\nTZw40WhlubOzs2bOnKmPPvrIWCYAAPGFYXccYNgNAAAASXr8+LHGjBmjSZMm6cWLF8ZyXV1dNXPm\nTFWtWtVYJgAgdlksFt26dUtBQUF68eKFbG1tlTlzZq7RnETxegOIin8qy3v06GH0TO60adNq+PDh\n6t69O2dyAwCSDIbdcYBhNwAAAP7N399f3bp10/bt243mfvnll5o0aZLy5MljNBcAAABA3Dh//ry6\ndeumbdu2Gc1t1KiRJk2apLx58xrNBQAgviXMCxwBAAAASZiTk5O2bdumNWvWKF++fMZyV65cKWdn\nZ+NnjgMAAACIXU+ePNGQIUPk5uZmdNDt4uKiX3/9VStXrmTQDQBIkhh2AwAAAPHAyspK//vf/+Tr\n66tBgwYZqxF89OiR+vbtq6JFi2rXrl1GMgEAAADEDovFonXr1snFxUVjxowxdm3utGnT6uuvv9ap\nU6f04YcfGskEACAhYtgNAAAAxKO0adNqzJgxOnPmjGrUqGEs19fXVx999JG+/PJLXbt2zVguAAAA\nADPOnz+vTz75RP/73/90+fJlY7lffvml/P391adPH67NDQBI8hh2AwAAAAmAo6Ojtm7dqrVr1yp/\n/vzGcn/88Uc5OTlp4sSJxs4SAQAAABB9jx8/1uDBg+Xm5qZffvnFWK6rq6t27dqlFStWKE+ePMZy\nAQBIyBh2AwAAAAmElZWV6tevL19fXw0ePNjYWRiPHz9W//79VbRoUf36669GMgEAAABEjcVi0dq1\na+Xi4qKxY8caezOqvb29Jk2apFOnTqlq1apGMgEASCwYdgMAAAAJTJo0aTR69GidPXtWNWvWNJbr\n5+enatWqqVGjRrp69aqxXAAAAACvFxAQoJo1a+rzzz/XlStXjOU2btxY/v7+6t27t1KmTGksFwCA\nxIJhNwAAAJBAFSpUSD///LPWrVtntNp81apVcnZ21oQJE6g2BwAAAGLR48ePNWjQILm5uWn79u3G\ncl1dXbV792798MMPyp07t7FcAAASG4bdAAAAQAJmZWWlevXqydfXV0OGDDFabT5gwAAVKVJEO3fu\nNJIJAAAA4G8Wi0Vr1qyRi4uLxo0bpxcvXhjJtbe31+TJk3Xq1Cl98MEHRjIBAEjMGHYDAAAAiUCa\nNGk0atQonTt3Tp988omxXH9/f1WvXl1ffPGF0TpFAAAAILny9/dXjRo11KBBA6M/Yzdp0kT+/v7q\n1asXleUAAPx/DLsBAACAROS9997Tli1btH79er3zzjvGcn/66SeqzQEAAIAYePz4sQYOHCh3d3ft\n2LHDWG7hwoW1Z88eLV++nMpyAAD+g2E3AAAAkMhYWVnps88+k4+Pj4YOHapUqVIZyX3y5MnLanOT\nv5wDAAAAkjKLxaLVq1fL2dlZ48ePN1ZZni5dOk2ZMkUnT55UlSpVjGQCAJDUMOwGAAAAEqk0adJo\n5MiROnfunGrVqmUs19/fXx9//LEaNGigy5cvG8sFAAAAkho/Pz99/PHHatiwoa5evWost2nTpvL3\n91fPnj2pLAcA4DUYdgMAAACJ3LvvvqvNmzdrw4YNcnBwMJa7Zs0aubi4aNy4cXr27JmxXAAAACCx\ne/To0ctWpJ07dxrLdXNz0549e7Rs2TLlypXLWC4AAEkVw24AAAAgCbCyslLdunXl4+OjYcOGGa02\nHzRokIoUKaLt27cbyQQAAAASK4vFop9++kkuLi6aMGGC0cryqVOnysvLi8pyAACigGE3AAAAkISk\nTp1aI0aM0Llz51S7dm1juQEBAapRo4Y+//xzqs0BAACQLPn5+al69er64osvjFaWN2vWTP7+/urR\noweV5QAARBHDbgAAACAJevfdd7Vp0yZt3LhRBQoUMJa7du1aOTs7a+zYsVSbAwAAIFl49OiR+vfv\nryJFiujXX381luvu7q69e/dq6dKlVJYDABBNDLsBAACAJKxOnTo6d+6cPD09ZWdnZyTz6dOnGjx4\nsNzd3bVt2zYjmQAAAEBCY7FYtGrVKjk7O2vixInGKsvTp0+vadOmycvLS5UrVzaSCQBAcmVlsVgs\n8b2JpK5kyZIKDAxUzpw5deLEifjeDgAAAJKpixcvqkePHtq0aZPR3Pr162vq1Kl65513jOYCSFqO\nHz+uTp06hVsrUaKE5s2b91bHlypVKtLM5Gzu3LmaP39+uLX27durY8eO8bSj6KtTp45u3LgRbm3j\nxo3KnTt3PO3o9Tw9PbV58+Zwa8OHD1edOnXifC8x/doCEDlfX1917drV6JncktS8eXNNnDhROXPm\nNJoLAEByxZndAAAAQDJRsGBBbdy4UZs2bVLBggWN5a5bt04uLi4aM2YM1eYAAABI1B4+fKh+/frF\nSmX5vn37tGTJEgbdAAAYxLAbAAAASGZq166tc+fOacSIEUarzYcMGSI3Nzdt3brVSCYAAAAQVywW\ni3788Uc5Ozvr66+/VkhIiJHc9OnTa/r06fLy8lKlSpWMZAIAgP/DsBsAAABIhuzs7DRs2DD5+Pio\nbt26xnIvXLigWrVqqX79+vrjjz+M5QIAAACxxcfHR9WqVdOXX36p69evG8tt0aKF/P391a1bN6VI\nkcJYLgAA+D8MuwEAAIBkrECBAtqwYYM2b95stNp8/fr1cnFx0ejRoxUcHGwsFwAAADDl4cOH6tu3\nr4oWLapdu3YZyy1SpIj279+v77//nspyAABiGcNuAAAAAPr000917tw5jRw50li1eXBwsIYOHSo3\nNzf9/PPPRjIBAACAmLJYLFq5cqWcnZ01adIko5XlM2bM0IkTJ1SxYkUjmQAA4PXoTgEAAAAg6e9q\n86FDh6pZs2bq2bOnNmzYYCT3999/16effqrPPvtM06ZNk4ODg5FcAMnL8ePH43sLCU7Hjh3VsWPH\n+N6GEZs2bYrvLSRapUqV4usDiIJz586pa9eu2r17t9Hcli1basKECcqRI4fRXAAA8Hqc2Q0AAAAg\nnAIFCmj9+vX6+eef9e677xrL3bBhg1xcXDRq1CiqzQEAABCnHj58qD59+qhYsWJGB91FixbVgQMH\ntHjxYgbdAADEA4bdAAAAACL1ySef6OzZsxo1apRSp05tJDM4OFjDhg2Tm5ubtmzZYiQTAAAAeBWL\nxaIVK1bI2dlZkydPNlZZniFDBn3zzTc6fvy4KlSoYCQTAABEHcNuAAAAAK9kZ2enIUOGyMfHR/Xq\n1TOW+/vvv6t27dqqW7euLl26ZCwXAAAA+Me5c+f04YcfqkmTJrp+/bqx3FatWsnf319dunRRihRc\nKRQAgPjEsBsAAADAGzk4OGjdunXaunWr3nvvPWO5mzZtkqurq0aMGKGnT58aywUAAEDy9eDBA/Xu\n3VtFixbVnj17jOUWK1ZMBw8e1KJFi6gsBwAggeBtZwAAAADeWs2aNXX27FlNmjRJY8aMMTKgDg4O\nlqenp5YsWaLp06erdu3aBnYKIDaFhITo7NmzunTpkoKCgmSxWJQuXTrlzZtXLi4uypAhQ3xvMdoe\nPnwoHx8fXblyRQ8fPpSVlZUyZcokJycnFSpUSDY2NlHKu379uvz9/XXz5k09fvxY6dKlU9asWVWk\nSBFlzZo1lp6FeVevXn35PJ4+fap06dIpU6ZMKlSokBwcHOJ7exFYLBZdu3ZN58+f17179/T48WM9\ne/ZMdnZ2srOzU8aMGZU7d27lzZtX6dOnj9W9hISEyM/PT7///rvu378vi8WijBkzvvw8iO3HN+n+\n/fsvvz4eP3788u8yb968Kly4cJS/PqLi6tWr8vPzU2BgoIKDg2VnZ6esWbPq3Xff1XvvvScrK6tY\ne2wkHv9Ulvfp00c3btwwlpshQwaNGTNGnTp1itXPcwAAEHUMuwEAAABESapUqTR48GA1a9ZMvXr1\n0tq1a43kXrx4UXXq1FHt2rU1ffp0FSxY0EguAHOuXr2q77//Xtu3b9fjx48jvY+NjY1KliypJk2a\nqGLFisYeu1SpUhHWjh8//lbHdujQQV5eXuHW5syZEy7zyJEjWr58uY4dO6bQ0NBIc7Jnz66GDRuq\nadOmsrW1feXjvXjxQuvXr9fatWt1/vz5SO9jZWUld3d3dezYUWXLln2r5/Ffc+fO1fz588OttW/f\nXh07dnzjscePH1enTp3CrZUoUULz5s17+fGzZ8+0fv16rVmzRhcvXnxlVs6cOVWnTh01b95cadKk\nieKz+FudOnUiDKY2btyo3LlzRynHy8tLmzZt0p49e/Tw4cO3OiZv3rxyd3dXhQoVVKlSJaVNmzZK\nj/kqV69e1dKlS7V9+/ZX7sXGxkZubm5q1aqVKlWqFK3HeZvX8nXe5mtr3759+uGHH+Tl5aWwsLBI\nc9KlS6cPPvhAHTp0UK5cud5y96/3/PlzrV27VmvWrHntZU+yZMmi2rVrq0mTJsqSJcvL9bf52kfS\ncfbsWXXp0kV79+41mtu6dWuNHz9e2bNnN5oLAADMoMYcAAAAQLS88847WrNmjbZt26ZChQoZy928\nebNcXV3l6elJtTmQQFgsFi1evFgNGzbUunXrXjnolqTQ0FAdO3ZMPXr0UM+ePXX//v2422g0PHr0\nSAMGDFCXLl10+PDhVw66JenWrVuaNWuWmjRpoqtXr0Z6Hx8fHzVq1EgTJkx45aBb+vvv1NvbWx4e\nHho1atRrHzc+nD17Vo0bN9bXX3/92kG3JAUGBmr+/PmqX7++Tp06FTcbjGQPPXv2VIcOHbRp06a3\nHnRLfw+lt27dqiFDhqh69eox3ss/Xy9ffPGF1qxZ89q9hIaG6vTp0+rZs6e6dev22q+t+HD79m11\n7dpVvXr10vHjx1856Jb+bkXYtGmTPv/8c61atSrGj3369Gk1bNhQkyZNeu2gW5Lu3Lmj77//Xg0a\nNNC2bdti/NhIXB48eKBevXqpWLFiRgfdxYoV06FDh7Rw4UIG3QAAJGAMuwEAAADESI0aNXTmzBmN\nHTtWqVOnNpL57NkzjRgxQoULF9amTZuMZAKInpCQEA0ePFgzZ87UixcvonTs/v371aZNG92+fTuW\ndhcz9+/fV7t27bRz584oHffHH3+oXbt2unnzZrj1/fv3q127drp8+XKU8jZs2CBPT88oHRObdu3a\npY4dO0b5edy5c0ceHh46evRoLO0scpcuXVLr1q21f//+GGc9f/48RseHhoZqyJAhmjlzZpSzDh06\npM6dO+vRo0cx2oMpf/zxh1q2bKnDhw9H6bjnz59r4sSJWrhwYbQfe9u2berYsaOuXbsWpeMePnyo\nIUOGaOnSpdF+bCQeFotFy5cvl5OTk6ZOnWrsTUMZM2bUrFmzdPz4cb3//vtGMgEAQOxh2A0AAAAg\nxlKlSqWBAwfKz89Pn3/+ubHcS5cuqW7duqpdu7Z+//13Y7kA3t6YMWO0ffv2V96eOXNmubi4qESJ\nEsqfP79SpAh/xbTLly+rV69eCgkJie2tRklISIh69uypCxcuhFtPmzatHB0dVbp0aTk7O7+ylvv2\n7dsaOHCgLBaLJOnUqVPq169fhAFnjhw5VLhwYZUsWVIODg6vvK7w1q1btXHjRgPPLGaOHTumwYMH\n69mzZ+HWs2TJIhcXF5UuXVqOjo5KlSpVpMc/e/ZMw4YNU1BQUFxsV0+fPlXXrl31119/RXq7tbW1\ncuTIIXd3d5UpU0YlSpSQo6NjrJ2lOXbsWP3yyy/h1mxsbJQ/f34VLVpUxYsXV758+V55vI+Pj6ZN\nmxYre4uKv/76Sx4eHhHe0JE2bVoVKlRIpUqVkqurqzJkyPDKjG+//VYnT56M8mMfOHBAw4cPf+X3\njFSpUsnBwUElS5aUq6truNryf8yYMSPKb2JB4nLmzBl98MEHatasmQIDA43ltmnTRgEBAfrqq6+4\nNjcAAIkE1+wGAAAAYEz+/Pm1evVqbd++XV27dlVAQICR3C1btmjnzp3q37+/BgwYYOwMcgCvt23b\ntle2K3zyySdq1KiR3Nzcwq0HBQXp119/1dy5c3Xnzh1Jfw/wYnKWZ2yYN2+ezpw58/Lj8uXLq0WL\nFipWrFi4gf3z58+1b98+TZ8+PcI1pb29vbVt2zaVK1dO/fv3f3nmu52dnZo2baratWtHGGzeuXNH\ny5Yt0w8//BDhLMTp06frww8/lL29vemn+1bu3bunwYMHh3sejRs3Vq1atVSgQIFw9w0ODtbevXs1\na9YsXb9+Pdxtd+7c0cyZMzV48OBY3/PChQsjHXS5u7uradOmKleu3Cv/Ph89eqTz58/r8OHD2r9/\n/2tr59/Gpk2bwl0f2sHBQW3atFHFihWVPn36cPe9deuWVqxYoRUrVkQY6q5fv161a9dWsWLFYrSf\nmBg8ePDLQbeVlZWqVaumRo0ayd3dPdwAMCwsTN7e3po1a1aEwbbFYtHo0aO1evXqV77J47/u37+v\nkSNHRnqGroODgzp06KCKFStGeBPK+fPntW7dOq1Zs0ahoaGyWCwaN25cpINwJG5BQUHy9PTUN998\nY/TyD8WLF9esWbM4kxsAgESIM7sBAAAAGPfxxx/L29tb48aNe+VZkVH17NkzjRw5Uq6urtq4cePL\nsykBxI779+9r8uTJEdZTpUqlKVOmaNSoUREG3ZKUIUMG/e9//9NPP/0Ubmjw7yFgQuDt7S1JSpEi\nhTw9PTVjxgyVKlUqwpnptra2qlatmhYtWqS8efNGyFm+fLmmTJnycrDv4OCgVatWqXPnzpGewZsl\nSxZ1795dI0eOjHBbUFCQduzYYeLpRculS5d07949SZKjo6NWr14tDw+PCINu6e9BeI0aNbRkyRI5\nOjpGuP3nn3+O9Tpui8US6ZsxGjVqpO+++07VqlV77RsH7O3tVbx4cX311VdasWKFlixZok8++STa\n+/n353jz5s31448/qlatWhEG3ZKUPXt2de/eXZMmTVLKlCkj3P7TTz9Fex8m/PNc0qdPr2+//Vbj\nxo1TsWLFIpzpam1trWLFimnu3Ln69NNPI+T8+eefUaq1nzRpku7evRth/X//+59WrFihjz/+ONKf\nKwoVKqR+/fpp4cKFypgxo6S/v57edL15JB4Wi0XLli2Ts7Ozpk2bZrSyfPbs2frtt98YdAMAkEgx\n7AYAAAAQK1KlSqUBAwbI19dXDRo0MJb7xx9/6LPPPlPt2rUj1A8DMOe77757Ofj8h7W1tcaNG6fK\nlSu/8fj06dPr66+/VpEiRWJri0aMGDFCtWvXfuP9smbNGumZyn5+ftq6daskKWfOnFqwYIFy5879\nxrwaNWpEOljdvHnzW+w6dhUoUEDz589Xzpw533jfjBkzauzYsREGts+ePXtt/b0J58+fj3A9+Dx5\n8qhXr16yto76r7xcXV01atSoGO+rbdu26t69+1tVIFesWFEtW7aMsL579+54v3a3nZ2d5s6dq1Kl\nSr3xvtbW1ho8eLDy588f4bZXtUP814ULF7Rt27YI65988okGDhwY6ZsC/qtw4cKaNWsWDTBJjLe3\nt6pUqaLmzZsbrSxv27atAgIC1LlzZyrLAQBIxBh2AwAAAIhV+fPn108//aTt27fLycnJWO7PP/+s\nwoULa9iwYXry5ImxXAB/Dyq3bNkSYf2zzz57q0H3P+zs7OTp6flWQ6r4UKtWLdWoUeOt7//P9apf\nZcSIES/PKn0bTZs2jbB27ty5lzXi8cHGxkbjxo1T2rRp3/oYBwcHVatWLcL66dOnTW4tgv9eT1r6\nu44+PodWRYoUUYcOHaJ0TPPmzSNcA/358+fy8/MzubUo69GjhwoVKvTW97e1tVWLFi0irL/t58Ga\nNWsirGXJkkX9+/d/6xp0SXJyclLbtm3f+v5IuIKCgtSjRw+VKFFC+/fvN5ZbokQJHT58WAsWLFC2\nbNmM5QIAgPjBsBsAAABAnKhevbq8vb01fvx4Y9Xmz58/16hRo+Tq6qoNGzZQbQ4YsnPnTj148CDc\nWqpUqeTh4RHlrPz58+uLL74wtTVjrKys1K5duygf96phf4kSJVSyZMkoZTk7OytHjhzh1kJCQuK1\nteKjjz7Se++9F+XjIht2+/r6mtjSKz1+/DjCWlSG9LGhffv2UR62p02bVuXLl4+wHtt/f6+TI0cO\n1atXL8rHffTRRxHOqg8MDNT9+/dfe9zz589fNiT8W9u2baN1DftmzZpxve5EzGKxaOnSpXJyctL0\n6dONVZZnypRJ3377rY4dO6Zy5coZyQQAAPGPYTcAAACAOGNra6v+/fvLz89PDRs2NJb7559/ql69\nevr000+pNgcMOHToUIS1KlWqROms5X/77LPPYrgj84oVKxZp5fKbvGoQ/DZV6G+b9+eff0Yry4To\nvlYuLi4R1q5cuRLT7bxWZEPQc+fOxepjvk727Nmjfc1fZ2fnCGuXL1+O6Zai7dNPP41w/fq3kS5d\nOuXJkyfC+puei7+/f4Ta9pQpU0apeeHfUqRIoZo1a0brWMQvb29vVa5cWS1atIi0vSG62rVrp4CA\nAHXq1InKcgAAkhiG3QAAAADiXL58+bRq1Srt2LEj0l/wR9fWrVtVuHBhDR06lGpzIAbOnj0bYS2y\nM3ffVsGCBVWwYMGYbMm4YsWKReu4XLlyGc2L7Pre8XWtZhsbm2hfYz179uwRqrhfvHihZ8+emdha\npN59990Ia7/99lu8Xfc8up8D0t//Lv5XfF6zu3jx4tE+NjrPJbLvOUWLFlWGDBmivY+oXHIB8S8o\nKEjdu3dXiRIldODAAWO5JUuW1JEjRzR//nxlzZrVWC4AAEg4GHYDAAAAiDfVqlXT6dOnNWHCBGPV\ns8+fP9fo0aPl6uqq9evXU20ORNH9+/d17dq1COuurq4xyi1cuHCMjjetQIEC0Tousu9VNjY20TpL\nXFKkl3WIryFnzpw5lTp16mgfH9nfTWw+l1y5ckX6JgpPT08NHDhQZ86cibXHjkxM3tAR2d9dZDXt\ncSW6Xx9S9D4PIqtsd3JyivYe/jk+Ktf6RvywWCxasmSJnJycNGPGDKOV5XPmzNHRo0dVtmxZI5kA\nACBhYtgNAAAAIF7Z2tqqX79+8vPzM3pd3z///FP169dXrVq1dP78eWO5QFJ348aNCGvp06dXzpw5\nY5RbqFChGB1vWvr06aN1nK2trbGsV+U9f/482nkxEZOzaCVFOLNbiv3n0qZNm0jXd+zYodatW6tO\nnToaP368fvnlF6OVyJGJyedBZH93sXlW/JvE5HMhOp8Hd+7cibAWk4G79HfNfbZs2WKUgdh1+vRp\nVapUSS1btjT29WllZaX27dsrICBAHTt2pLIcAIBkgGE3AAAAgAQhb968+vHHH7Vz585Ir/0aXdu2\nbZObm5sGDx4cr2fJAYnFgwcPIqxlypQpxrmZM2eOcYZJdnZ2CTJLUrw1Uph+HlLsP5eaNWuqTp06\nr7z9xo0bWr16tQYPHqxPP/1UtWrV0pAhQ7R+/XoFBgYa3UtMzoqPTHw2k8T1c3n48GGEtXTp0sX4\ncSO7rjvi3/3799WtWzeVKFFCBw8eNJZbqlQpHTlyRPPmzaOyHACAZIRhNwAAAIAE5aOPPtKpU6c0\nceJEo9XmY8eOlaurq9auXUu1OfAakQ2dTHwtMnRCbBk6dKjatm37Vmdw3rp1S9u2bdPo0aNVp04d\ntW/fXps3b1ZISEgc7BSvElnNOd93kp6wsDB9//33cnJy0jfffKOwsDAjuZkzZ9bcuXN15MgRlSlT\nxkgmAABIPBh2AwAAAEhwbG1t1bdvX/n5+alRo0bGci9fvqzPP/9cNWvWVEBAgLFcICl58eJFhLWU\nKVPGONdEBhAZa2trde7cWT/++KNq1KgRaTV8ZCwWi06ePClPT081aNBAR44cieWd4lUie6OCiUGo\nqes/I+ZOnz6typUrq1WrVrp165aRTCsrK3Xo0EEBAQHq0KEDleUAACRTDLsBAAAAJFh58+bVypUr\n9euvvxqtNt++fbvc3Nw0aNAgqs2B/4jsTMgnT57EOJevNcQ2BwcHjRkzRr/88os8PT1Vq1Yt5ciR\n462OvXr1qrp27aqlS5fG8i4Rmcgqy018z4jsjHHErfv376tr167GK8tLly6to0ePau7cucqSJYux\nXAAAkPgw7AYAAACQ4H344Yc6ffq0Jk2aZKyS9MWLFxo3bpxcXFy0Zs0aqs2B/y+yoZOJgRFDJ8SV\ndOnSqXbt2ho5cqS2bNmiTZs2adSoUapfv77y58//yuMsFotmzJihPXv2xN1mISny7zv37t2Lce79\n+/djnIHoCQsL0+LFi+Xo6KiZM2carSyfN2+ejhw5otKlSxvJBAAAiRvDbgAAAACJQsqUKdW7d2/5\n+fmpcePGxnKvXLmiBg0aUG0O/H8ZM2aMsHbr1i09e/YsRrmXL1+O0fFAdOXKlUuffPKJBg8erLVr\n12r16tVq27atMmXKFOG+FotF06ZN4xrecSxnzpwR1s6fPx+jzFu3bikoKChGGYiekydPqmLFimrd\nurX++usvI5lWVlbq2LGjAgIC1L59e1lb82ttAADwN34qAAAAAJCo5MmTRz/88IN27dolV1dXY7n/\nVJsPHDiQumUka3nz5pWdnV24tdDQUF24cCFGubyZBAmFg4ODOnfurHXr1qlSpUoRbr969aq8vb3j\nYWfJV+HChSOsnTt3LkaZPj4+MToeUXfv3j116dJFpUqV0uHDh43lli5dWseOHdOcOXOoLAcAABEw\n7AYAAACQKFWtWlWnTp3S5MmTjVabjx8/Xs7Ozlq9ejXV5kiWUqRIIRcXlwjrx44di3ZmcHCwTp8+\nHZNtAcbZ29tr7NixkQ7PTp06FfcbSsbc3d0jrAUEBMSoEWL79u0x2RKiICwsTIsWLZKTk5NmzZpl\nrLI8S5Ysmj9/vo4cOaJSpUoZyQQAAEkPw24AAAAAiVbKlCnVq1cv+fv7q0mTJsZyr169qoYNG+rj\njz+Wn5+fsVwgsShSpEiEta1bt0Y7b9++fTQmIEFKnTp1pGd337lzJx52k3w5ODgoT548EdbXrVsX\nrby7d+9q7969Md0W3oKXl5cqVKigNm3aGK0s79SpkwICAtSuXTsqywEAwGvxkwIAAACARC937txa\nvny5du/eHWkVanTt3LlTRYoU0YABA/To0SNjuUBCV6tWrQhrFy9e1IEDB6KcFRYWpiVLlpjYFhAr\nIrtOvakzU/F2rKysVL9+/QjrK1eu1B9//BHlvGnTpunZs2cGdoZXuXfvnjw8PFS6dGkdOXLEWG6Z\nMmV07Ngxffvtt8qcObOxXAAAkHQx7AYAAACQZHzwwQc6efKkpkyZonTp0hnJfPHihSZMmCAXFxf9\n9NNPVJsjWXj33XcjPbt78uTJCg4OjlLWmjVraEhAgnb16tUIa9myZYuHnSRvdevWVapUqcKtvXjx\nQgMHDtSDBw/eOmf9+vX6+eefTW8P/19YWJgWLlwoR0dHzZ4922hl+YIFC3T48GEqywEAQJQw7AYA\nAACQpKRMmVI9e/aUv7+/mjZtaiz36tWr+uKLL1S9enUGd0gWWrRoEWHtypUr6tevn0JCQt4q4/Dh\nw5oyZYrprQGSpLVr1+rnn39+68/HyFy9elX79++PsO7q6hqTrSEaMmfOrPbt20dYP3/+vDp37qyL\nFy++9viQkBAtXrxYY8eOfblmZWVlfJ/J2T+V5W3bttXt27eNZFpZWalz584KCAhQ27ZtqSwHAABR\nxk8PAAAAAJKkXLlyadmyZdqzZ4/c3NyM5f76668qUqSI+vfvT7U5krQPPvhAVatWjbB+6NAhdejQ\nQX/++ecrjw0NDdWSJUvUp08fvXjxQpJkZ2cXa3tF8nTp0iUNGzZMn332mebPnx/luusLFy6oW7du\nEequs2TJotKlSxvcKd5W8+bNI32jgb+/v5o0aaIRI0bowIEDCgwM1PPnzxUUFKQLFy5oyZIlatKk\niWbOnPnyTGNHR8dIGyoQdXfv3tVXX32lUqVKGa0sL1u2rH777TfNnj2bynIAABBtKeJ7AwAAAAAQ\nm6pUqSIvLy/NmjVLw4YN08OHD2Oc+eLFC02cOFHLly/XlClT1LBhQ84eQ5LUv39/eXl5KSgoKNy6\nt7e3GjVqpLJly6pSpUrKmTOn7OzsdPv2bfn7+2v79u26efPmy/vb2NioU6dOmjZtWhw/AyQHN2/e\n1Ny5czV37ly9++67KlGihFxcXOTo6KhMmTIpffr0srW11dOnTxUYGKiAgADt2bNHe/fuVWhoaIS8\nrl27ysbGJh6eCWxsbDRu3Di1adNGd+7cCXdbSEiINm3apE2bNr0xJ126dBo7dmy4s7z/wZnDby8s\nLEyLFi3SgAEDjJ3JLUlZs2bVhAkT1KpVK14PAAAQYwy7AQAAACR5KVOmVI8ePdSoUSP169dPy5Yt\nM5J77do1NWrUSHPnztXMmTPl4uJiJBdIKLJmzaopU6aoS5cuevr0abjbQkJCdPDgQR08ePCNOX37\n9pWDg0Ms7RL4P7///rt+//33aB9fu3Zt1a5d2+COEFV58uTR3Llz1b17d127di3Kx2fIkEFTpkyR\ng4NDpNeTTpMmjYltJnknTpyQh4eHjh49aizzn8ryUaNGcSY3AAAwhrfOAQAAAEg2cuXKpaVLl2rv\n3r1yd3c3lrtr1y4VKVJEffv2NXLmOJCQFC1aVN9++62yZs0a5WOtra3Vu3dvNWjQIBZ2BphjZWWl\npk2bavjw4fG9FUhycHDQsmXLVKdOnSid+VuyZEl9//33Klq0qCRF+m+yvb29sX0mRXfv3lXnzp1V\nunRpo4PucuXK6fjx45o1axaDbgAAYBTDbgAAAADJTuXKleXl5aVp06Ypffr0RjJDQkI0adIkOTs7\na+XKlbJYLEZygYTAzc1NK1asUJ06dd663tnR0VHz589X48aNY3l3SK5q1KihunXrKkuWLDHKKVy4\nsBYsWKCePXtySYoEJF26dBo+fLhWrlypxo0bK1++fJHeL0uWLKpVq5bmzJmjuXPnKm/evC9ve/To\nUYT7M+yOXFhYmBYsWCBHR0fNmTPH2M8xWbNm1cKFC3Xw4EGVKFHCSCYAAMC/WVn4DUysK1mypAID\nA5UzZ06dOHEivrcDAAAA4F8CAwPVr18/LV261Ghu1apVNXPmTLm6uhrNBeJbYGCgfv75Zx0/flwX\nL15UUFCQLBaL7O3tlTdvXrm7u6tKlSoqVapUfG8VyYTFYlFAQIC8vb3l7e2tCxcu6Nq1a3ry5Emk\n97e3t1ehQoVUtGhR1ahRQ4UKFYrjHSO6Hj16pJs3byo4OFh2dnbKkiWLMmbM+Mr7Vq1aNdzQNlWq\nVNq3bx/XZP+P48ePy8PDQ8eOHTOWaW1t/bKyPFOmTMZyAQAA/othdxxg2A0AAAAkfPv375eHh4fO\nnDljLDNFihTq3r27hg8frnTp0hnLBQC82b179/Tw4cOXQ++0adPK3t6ewVsycfToUXl4eIRbc3Nz\n0+LFi+NnQwnQnTt3NHjwYM2bN89oI83777+vWbNmqXjx4sYyAQAAXoUacwAAAACQVKlSJXl5eWn6\n9OlGq80nT54sZ2dnrVixgmpzAIhDmTJlUv78+eXs7CxnZ2fly5ePQXcysnPnzghrtK38LSwsTPPn\nz5eTk5Pmzp1r7OeTbNmyadGiRTpw4ACDbgAAEGcYdgMAAADA/5ciRQp169ZNAQEBatmypbHc69ev\nq0mTJvrwww917tw5Y7kAACCi+/fva+vWrRHWGcD+XVn+/vvvq0OHDrpz546RTGtra3Xp0kX+/v5q\n1aqVrK35lTMAAIg7/OQBAAAAAP+RI0cOLV68WAcOHFDRokWN5e7Zs0fFihVT79699eDBA2O5AADg\n/4wePVrBwcHh1jJmzKgqVarE047i3507d9SxY0eVKVPG6LW5y5cvrxMnTuibb76hOQEAAMQLht0A\nAAAA8AoVKlTQ8ePHNWPGDGXIkMFIZkhIiKZMmSJnZ2f98MMPVJsDAPAv169f16lTp6J1bGhoqCZP\nnqw9e/ZEuK1u3bqytbWN2eYSodDQUM2bN0+Ojo5Gr82dLVs2LV68WPv371exYsWMZAIAAEQHw24A\nAAAAeI0UKVKoa9euL6s5Tblx44aaNm2qqlWr6uzZs8ZyAQBIzG7duqV27dqpQ4cO+uWXX/T06dO3\nOs7b21tfffWVVqxYEeG2TJkyqVmzZqa3muD99ttvKleunDp27Ki7d+8aybS2tlbXrl1fXvKFynIA\nABDfrCycRhDrSpYsqcDAQOXMmVMnTpyI7+0AAAAAiIFDhw7Jw8Mj2medRcbGxkbdunWTp6en0qdP\nbywXAIDE5tSpU2rXrt3Lj+3s7FS8eHG5uLioYMGCypAhg1KnTq1Hjx4pKChI/v7+On78uAICAl6Z\nOWXKFFWuXDkutp8g3L59W4MGDdKCBQuMNshUqFBBM2fO5ExuAACQoDDsjgMMuwEAAICkJSQkRHPm\nzNGQIUMUFBRkLDdnzpyaNGmSmjRpIisrK2O5AAAkFv8ddseElZWVunbtqhYtWhjJS+hCQ0O1YMEC\nDRo0yNiZ3JKUPXt2ff3112revDk/nwAAgASHnhkAAAAAiKIUKVKoS5cuCggIUOvWrY3lBgYGqlmz\nZvrggw905swZY7kAACQ3qVOn1vjx45PNoPvYsWMqW7asOnXqZLSyvFu3bvL391eLFi0YdAMAgASJ\nYTcAAAAARFP27Nm1cOFCHTp0yGil5759+1S8eHH17NnT6JnjAAAkdPny5VP9+vWVMWPGaB2fJk0a\ntWjRQhs2bNBHH31kdnMJ0O3bt9W+fXuVK1fOaKNkxYoV5eXlpenTp0f7tQAAAIgL1JjHAWrMAQAA\ngKQvNDRUc+fO1eDBg3X//n1juTly5NCkSZPUtGlTzqgCACQboaGh8vPz05kzZ+Tr66vr168rMDBQ\njx49UnBwsCwWi9KlS6f06dMrS5YscnNzU4kSJVS8eHGlTZs2vrcf60JDQzV//nwNGjRI9+7dM5ab\nI0cOff3112rWrBk/dwAAgESBYXccYNgNAAAAJB9//fWXBgwYoIULFxrNrVSpkmbOnKkiRYoYzQUA\nAInLkSNH5OHhIS8vL2OZ1tbW6tq1q0aMGKEMGTIYywUAAIht1JgDAAAAgEHZsmXTd999p0OHDql4\n8eLGcvfv368SJUqoR48eVJsDAJAM/fXXX2rbtq3ef/99o4PuihUr6uTJk5o2bRqDbgAAkOgw7AYA\nAACAWPD+++/rt99+0+zZs5UpUyYjmaGhoZo+fbqcnJy0ZMkSUdQFAEDSFxoaqtmzZ8vR0dFoc0yO\nHDm0dOlS7du3j+YYAACQaDHsBgAAAIBYYmNjo86dO8vf319t27Y1lnvz5k21bNlSlStX1unTp43l\nAgCAhOXw4cMqXbq0PDw8dP/+fSOZNjY26tGjh/z9/bk2NwAASPQYdgMAAABALMuWLZsWLFigw4cP\nq0SJEsZyDxw4oBIlSqh79+7GfgEOAADi361bt9SmTRuVL19eJ0+eNJZbqVIlnTx5UlOnTqWyHAAA\nJAkMuwEAAAAgjpQrV07Hjh3Tt99+a6zaPCwsTDNmzJCTk5O+//57hYWFGckFAABxLzQ0VLNmzZKT\nk5MWLVpkLDdnzpxatmyZ9u7dK3d3d2O5AAAA8Y1hNwAAAADEIRsbG3Xq1EkBAQFq166dserQW7du\nqVWrVlSbAwCQSB06dEilSpVSly5djFaW9+zZU35+fmratCmV5QAAIMlh2A0AAAAA8SBr1qyaP3++\njhw5olKlShnLPXjwoEqUKKFu3bpRbQ4AQCJw8+ZNtWrVShUqVNCpU6eM5VauXFmnTp3SlClTqCwH\nAABJFsNuAAAAAIhHZcqU0ZEjRzRnzhxlzpzZSGZYWJi++eYbOTk5afHixVSbAwCQAIWEhLz89/r7\n7783lpsrVy4tX75ce/bskZubm7FcAACAhIhhNwAAAADEMxsbG3Xs2FH+/v5q37690Wrz1q1bq2LF\nijp58qSRTAAAEHMHDhxQyZIl1a1bNwUFBRnJtLGxUa9eveTn56cmTZpQWQ4AAJIFht0AAAAAkEBk\nzZpV8+bN09GjR41Wmx8+fPjlNUDv3btnLBcAAETNzZs31bJlS1WqVEne3t7Gcj/44AOdPn1akydP\nVvr06Y3lAgAAJHRWFovFEt+bSOpKliypwMBA5cyZUydOnIjv7QAAAABIBEJDQ/Xdd99p4MCBunv3\nrrHcbNmyacKECWrZsqWsrXn/M5CcXLlyRVeuXAm3li9fPuXLly+edgQkHyEhIZo9e7aGDh2qBw8e\nGMvNlSuXpkyZokaNGnEmNwAASJYYdscBht0AAAAAouvOnTsaPHiw5s2bJ5P/+1auXDnNmjVLJUqU\nMJYJIGGbO3eu5s+fH26tffv26tixYzztCEge9u/fry5duhg9kztFihTq0aOHhg0bpnTp0hnLBQAA\nSGx4Gz8AAAAAJGBZsmTRnDlzdOzYMZUuXdpY7pEjR1S6dGl5eHhQbQ4AQCwIDAxU8+bNVblyZaOD\n7qpVq+r06dP6+uuvGXQDAIBkj2E3AAAAACQCpUqV0pEjRzR//nxlyZLFSGZYWJhmz54tR0dHLVy4\nUGFhYUZyAQBIzkJCQjRt2jQ5OTlp2bJlxnJz586tlStX6tdff5Wrq6uxXAAAgMSMYTcAAAAAJBLW\n1tZq166d/P391alTJ2PX5rx9+7batm2rChUqyMvLy0gmAADJ0b59+1S8eHH17NnT2LW5U6RIob59\n+8rPz49rcwMAAPwHw24AAAAASGSyZMmib7/9VseOHVOZMmWM5R45ckSlSpXSV199pbt37xrLBQAg\nqbtx44aaNWumKlWq6OzZs8ZyP/roI3l7e2vixIlUlgMAAESCYTcAAAAAJFKlSpXS4cOHtWDBAmPV\n5haLRd9++62cnJz03XffUW0OAMBrvHjxQlOnTpWTk5OWL19uLDdPnjxatWqVduzYIRcXF2O5AAAA\nSQ3DbgAAAABIxKytrdW2bVsFBASoc+fORqvN27Vrp/Lly+vEiRNGMgEASEr27t2r4sWLq1evXnr4\n8KGRzJQpU6p///7y8/NTw4YNqSwHAAB4gxTxvQEAAAAAQMxlzpxZs2fPVtu2beXh4aGjR48ayT16\n9KhKly6tjh07asyYMcqcObORXCAp+OOPP/T777/r1q1bevLkiWxsbJQ+fXq9//77ypUrV5Syrl69\nqosXLyowMFBPnjyR9PfXdebMmVWoUCHlyJEjNp5CshYSEiJ/f3/9+eefunv3roKDg2Vra6tMmTKp\nevXqsrOzi1ZucHCwfH199ccffygoKEhWVlbKlCmTsmfPrqJFiyp16tSGn8nfrRzXrl3T+fPnde/e\nPT1+/FjPnj2TnZ2d7OzslDFjRuXOnVt58+ZV+vTpjT9+cnP9+nX16dNHK1asMJpbrVo1ffPNN3J2\ndjaaCwAAkJRZWSwWS3xvIqkrWbKkAgMDlTNnTs6IAAAAABDrwsLCtHjxYvXv31+3b982lpslSxaN\nHz9ebdq0kbU1RWFIejZt2qQRI0aEW6tdu7Y8PT1ffhwYGKgff/xR27Zt019//RVpzvDhw1WnTp03\nPt758+e1du1a7dmz55VZ/3B0dFSVKlXUuHHjtx5WXr9+XXXr1n2r+75Jrly5tGnTpkhvK1WqVIS1\n48ePR/uxPD09tXnz5nBrb/t3+jbHnj17VitXrtT+/fv1+PHjSHM2btyo3Llzv/y4Q4cO8vLyCnef\nOXPmhHvuAQEBWrJkifbs2aPg4OBIc1OmTKmSJUuqffv2Klq06Bufz5t4eXlp06ZN2rNnz1ufWZw3\nb165u7urQoUKqlSpktKmTRvjfSQXL1680IwZM+Tp6alHjx4Zy82bN6+mTp2qzz//nDO5AQAAoogz\nuwEAAAAgibG2tlabNm1Ur149DR06VHPmzDFy7e07d+6offv2mj9/vmbNmhXpgAtIypYtW6Zvv/1W\nz549i1FOYGCgJk+erN27d7/1MQEBAQoICNCqVavUrl07ffnllwzFoujp06eaOHHiK4f20RUSEqJv\nvvlGK1aseOP32hcvXujIkSM6cuSI6tSpo8GDBytFiqj/ei4wMFATJkzQ/v37o3zs1atXdfXqVW3d\nulW2trY6dOhQlDOSo927d6tLly7y8fExlpkyZUr17t1bgwcPlr29vbFcAACA5IS34gMAAABAEpU5\nc2bNmjVLx48f1/vvv28s99ixYypTpow6deqkO3fuGMsFEiqLxaIRI0Zo2rRpMR5079u3T19++WWU\nBt3/FhQUpMmTJ2vIkCEKCQmJ0V6SkwcPHqhdu3bGB91Pnz5Vly5dtHz58ii/qWjTpk3q3bt3lF/H\nS5cuqXXr1tEadP/X8+fPY5yR1F27dk2NGzfWhx9+aHTQXb16dZ05c0bjxo1j0A0AABADDLsBAAAA\nIIkrXry4Dhw4oIULFypbtmxGMi0Wi+bOnStHR0fNnz/fyJnjQEI1e/bsSIek2bJlk4uLi0qWLCkH\nB4c3Xot58+bN6tOnzyvrj21sbJQ/f34VKVJEJUuWVIECBV551u8vv/yinj17KjQ0NOpPKJkJDQ1V\n79695e/vH27d2tpaefPmVZEiRVSsWDHlyZMnSmdZh4WFqW/fvhEq21OmTKkCBQqoRIkSKlKkiHLm\nzPnKjIMHD+r7779/68d8+vSpunbt+srae2tra+XIkUPu7u4qU6aMSpQoIUdHR2XPnv2tHwN/e/Hi\nhSZNmiRnZ2etXLnSWG6+fPm0evVq/fLLL3JycjKWCwAAkFzFa435mTNndOPGjXBr+fLlk4uLSzzt\nCAAAAACSJmtra7Vu3fpltfm3335rZEB99+5ddejQ4WW1eenSpQ3sFkg4zp07pz///PPlx2nTplWz\nZs1Uo0YN5c+fP9x9Q0JCtG/fvkjfVHL69GmNGjUq0q+74sWLq3HjxipTpkyEMzwfPXqk/fv3a968\nebpy5Uq42w4fPqzvvvtOHTp0iHTvWbNm1aJFi15+vH79em3YsCHcfT777DPVq1cv8if/LylTpnzj\nfRKqH374QRcvXnz5cZ48edSmTRtVrlxZmTJlCnffhw8fauvWrUqTJs0bcxcsWBDuOt6FCxdW69at\nVaZMmQjHX758WYsXL9amTZtksVgi5NSsWVN58uR542MuXLhQgYGBEdbd3d3VtGlTlStX7pVnCT96\n9Ejnz5/X4cOHtX//fp0/f/6Nj5dc7dq1S126dJGvr6+xzJQpU6pv374aNGgQ10kHAAAwKF6H3UOH\nDtWJEyfCrS1dupRhNwAAAADEkkyZMmnmzJlq27atPDw8dPjwYSO5v/32m8qWLat27dpp7Nixypo1\nq5FcIL5dunTp5X+7urpqypQpr/z8TpEihT788MMI6w8ePNDgwYMjnIWdJk0aDR48WDVq1Hjl49vb\n2+uTTz5RtWrVNGbMGG3evDnc7d99953Kly8vNze3CMfa2trK3d395ceRXZs5e/bs4e6TFP170F2v\nXj3169dPtra2kd43Xbp0+uKLL94q959Bt7W1tXr06KEmTZq88r758+fXsGHDVKRIEY0ePTrcbS9e\nvND69evl4eHx2sezWCyRNgw0atRIvXv3lrX16wsc7e3tVbx4cRUvXlxfffWVfHx8tGLFitcek9xc\nvXpVvXv31qpVq4zm1qhRQzNmzJCjo6PRXAAAAMRzjfnvv/8ui8Xy8k+GDBlUpUqV+NwSAAAAACQL\n/1SbL1q0yGi1+fz58+Xk5KS5c+dSr4wkpVChQvr222+j9UaOGTNmRDgb187OTt9+++1rB93/ljJl\nSnl6eka4f2hoqBYsWBDlPSVHderU0ZAhQ1456I6uQYMGvXbQ/W/16tVTrVq1Iqz/900MkTl//rxu\n374dbi1Pnjzq1avXGwfdkXF1ddWoUaOifFxS9Pz5c02cOFHOzs5GB9358+fX2rVrtXXrVgbdAAAA\nsSReh90PHjyQlZXVyz+urq6ysrKKzy0BAAAAQLJhbW2tVq1aKSAgQF26dInWsCQyd+/eVadOnVSu\nXDkdO3bMSCYQn2xsbDR8+PBoVQ/fvn1bW7ZsibA+aNAgFS5cOMp5gwYNUo4cOcKtHTx4UJcvX45y\nVnKSM2dO9e3b13hu9erV36oG/t/at28fYe2vv/7StWvXXnvczZs3I6yVL19eNjY2UXp8hLdz504V\nLVpU/fv31+PHj41k2traavDgwfL19VX9+vX5fScAAEAsitdht52dnSS9vFaRqbMJAAAAAABvL2PG\njPrmm2904sQJVahQwVju8ePHVa5cObVv3z7C2YhAYlKlShU5OztH69iVK1fqxYsX4dbc3NwiPbv3\nbaRNm1aNGzcOt/aqemv8n+bNm7/VdbijwsrKSh07dozycfny5ZOTk1OE9TddHzqyQSzXfo6+K1eu\n6IsvvlD16tXl5+dnLLdmzZo6e/asRo8ebfxzDgAAABHF67A7Q4YM4T7+Z+gNAAAAAIh7xYoV0/79\n+/X9998re/bsRjItFosWLFggR0dHzZkzh2pzJEqfffZZtI/dvn17hLUvv/wyJtuJdFB+6tSpGGUm\nZba2ttF+c8HrFClSRA4ODtE61sXFJcLalStXXnuMvb19hLVz585F6/GTs+fPn2vChAlydnbWTz/9\nZCz3nXfe0bp16/Tzzz+rUKFCxnIBAADwevE67HZwcJDFYnlZ5cM7/QEAAAAgfllZWalFixby9/dX\nt27djFWb37t3T507d1bZsmV19OhRI5lAXLC2tlaJEiWidezNmzd1/fr1cGspU6ZUpUqVYrSnzJkz\n65133gm35uPjo5CQkBjlJlWOjo5Kly6d8dzixYtH+9i8efNGWHv06NFrj3n33XcjrP32229vdb1v\n/G3Hjh0qUqSIBgwYoCdPnhjJtLW11dChQ+Xj46N69epRWQ4AABDH4nXY7e7u/vK/LRaL/vzzz3jc\nDQAAAADgHxkzZtT06dPl5eWlihUrGss9ceKEypUrp3bt2umvv/4ylgvEFgcHB6VOnTpax3p5eUVY\ny58/v5Hq6dy5c4f7+NmzZ1y3+xUiO4vahAIFCkT72MjO0n7TsDtXrlwqWLBghHVPT08NHDhQZ86c\nifZ+krrLly+rQYMG+vjjj+Xv728st1atWjp37pxGjhxJZTkAAEA8SRGfD16lShXNnTv35cfXr1/X\n+fPnqfoBAAAAgASiaNGi2rdvn5YtW6a+ffvq5s2bRnK/++47rV27VmPGjFGHDh1kY2NjJBcwLSaV\n/r///nuEtQwZMhgZSoaFhUVYe/DgQYxzkyJTl2X4r/9eni8qUqVKFWHt+fPnbzyuTZs2GjJkSIT1\nHTt2aMeOHcqVK5cqVKig4sWLq1ixYsqRI0e095gUPHv2TFOmTNHo0aONnckt/f0mmOnTp6tOnTqc\nyQ0AABDP4nXYXbFiReXOnVs3btx4ubZq1SoNHjw4HncFAAAAAPg3KysrNW/eXHXr1tXw4cP1zTff\nRDpoi6p79+7pq6++0oIFCzRr1iyVK1fOwG4BsyI7A/dtBQUFRVjz8vJS69atY7KlKD0eYvYavo6d\nnZ3RPIvF8sb71KxZU0ePHtWmTZsivf3GjRtavXq1Vq9eLenvQX+JEiVUqlQplStXTjlz5jS654Ts\nl19+UdeuXXX+/HljmalSpVL//v01YMCAaDc+AAAAwKx4rTG3trZWp06dXl6322KxaOHChdRuAQAA\nAEAClCFDBk2bNk0nT540Wm3u5eWl999/X23btqXaHAlOTAaacT18flMNdnJleigd34YOHaq2bdu+\nVSPGrVu3tG3bNo0ePVp16tRR+/bttXnz5iR9fffLly/r888/V82aNY0Ouj/99FOdO3dOI0aMYNAN\nAACQgMTrsFuSWrVqpSJFikj6+2yBZ8+eqXXr1rp792487wwAAAAAEJkiRYpo3759Wrp0qdGK3IUL\nF8rR0VGzZ89WaGiosVwgvsT18NlE4wISPmtra3Xu3Fk//vijatSoIVtb27c6zmKx6OTJk/L09FSD\nBg105MiRWN5p3Hr27JnGjh0rZ2dnrV271lhugQIFtHHjRm3evFnvvvuusVwAAACYEe/Dbmtray1Y\nsODl9ZOsrKzk7++vhg0b6uzZs/G8OwAAAABAZKysrNSsWTP5+/urR48exq65ff/+fXl4eKh06dI6\nfPiwkUwgvnAtesQmBwcHjRkzRr/88os8PT1Vq1att34D0tWrV9W1a1ctXbo0lncZN7Zt2yZ3d3cN\nHjxYT58+NZKZKlUqeXp66ty5c6pTp46RTAAAAJgXr9fs/kfu3Lm1bt06NW3aVJcuXXo58K5du7aa\nNGmiJk2ayM3NLb63CQAAAAD4jwwZMmjq1Klq06aNPDw8tH//fiO5J0+eVPny5dW6dWuNHz/+5Ruk\ngcQkbdq0EdaqV6+ucePGxcNuEo+kXLEdG9KlS6fatWurdu3akv6+bvepU6fk5eWlEydOvPJygRaL\nRTNmzFC+fPn0wQcfxOGOzfnjjz/Us2dPrV+/3mhunTp1NG3aNBUsWNBoLgAAAMyL92H3vyuTPD09\nNX78ePn6+srKykohISFaunSpli5dqoIFC6pYsWJyc3NT9uzZZW9vH+n/NEZHuXLljOQAAAAAQHLl\n7u6uvXv36ocfflCfPn0UGBhoJHfRokVat26dRo8erU6dOnGmLBKVyM6yjevreMcFGxubCJceCAkJ\nUYoU0fu1U1L8O4pLuXLlUq5cufTJJ59I+nsgvHXrVq1du1b37t0Ld1+LxaJp06apYsWK0X694kNw\ncLAmTZqksWPHGjuTW5IKFiyo6dOnv3zjAAAAABK+eP8ptkGDBrKysor0NisrK1ksFknS77//rosX\nLxq95s4/j/Gqd7gCAAAAAN6elZWVmjZtqjp16sjT01MzZswwcu3t+/fvq0uXLlqwYIFmzZql8uXL\nG9gtEPsKFCgQYe3GjRvxsJPYlSZNGj18+DDc2tOnT5UuXbpo5d26dcvEtvD/OTg4qHPnzmrevLmG\nDh0aoYHj6tWr8vb2VokSJeJph1GzdetWde3aVb///ruxTDs7Ow0cOFD9+vWTnZ2dsVwAAADEvni/\nZvc/LBbLyz//fCz9/cuSf/78+z4m/wAAAAAAzEmfPr2mTJmiU6dOqXLlysZyT506pQoVKqh169YM\nw5AoFClSJMLalStXdPPmzXjYjV55skFM2dvbR1i7c+dOtLIePnyoS5cuxXRLiIS9vb3Gjh2rLFmy\nRLjt1KlTcb+hKPrjjz9Ur1491apVy+igu27duvLx8dGwYcMYdAMAACRCCWbY/e+h9j/+O5D+931M\n/AEAAAAAxB43Nzft2bNHy5cvV65cuYzlLl68WI6Ojvrmm2+4ti8StIIFCypPnjwR1nfv3h0Pu5Fs\nbW0jrJn4GsqWLVuEtfPnz0cra//+/QoLC4vplvAKqVOnVqVKlSKsR/fNCXEhODhYo0aNkouLizZs\n2GAst2DBgtq8ebM2bNgQaQsDAAAAEocEM+z+NwbTAAAAAJA0WFlZqUmTJvLz81OvXr2MXXM7KChI\n3bp17WjDOwAA879JREFUU6lSpXTw4EEjmUBsqFWrVoS1JUuW6NmzZ3G+lzRp0kRYCw4OjnGuk5NT\nhLUjR45EOcdisWj58uUx3g9eL2PGjBHWEuobDLZs2SI3NzcNGzbMyOeq9Hdl+ciRI3Xu3Dl9+umn\nRjIBAAAQfxLEsDu26smpLwcAAACAhCF9+vSaPHmyTp06pSpVqhjLPX36tCpWrKiWLVvGWzU08Dqf\nf/55hGrkW7duadKkSXG+l/Tp00dYu379eoxzXV1dI6zt2rUrwnW832T58uXy9/eP8X7welevXo2w\nFtnZ+fHp0qVLqlu3rmrXrm20srxevXry9fXV0KFDqSwHAABIIlLE9wZ++umn+N4CAAAAACCOuLm5\naffu3Vq5cqV69+6tGzduGMldsmSJ1q9fr1GjRumrr75SihTx/r+7gCQpa9asatmypebOnRtufd26\ndcqQIYO++uorWVtH/1yEkJAQ7dixQ+7u7sqbN+9r7xtZVfPZs2dlsVhi1KpXqVIlpUyZUi9evHi5\n9vDhQ02bNk1Dhw59q4xdu3Zp1qxZ0d5DcrB27VrZ2dnp448/jvb3uKtXr2r//v0R1iN7w0J8ePr0\nqSZOnKjx48cbO5Nbkt577z3NmDFDn3zyibFMAAAAJAzx/n//77//fnxvAQAAAAAQh6ysrNS4cWPV\nrl1bI0eO1LRp04xcN/jBgwfq3r27vvvuO82aNUsVK1Y0sFsg5lq3bq39+/fLx8cn3PrixYvl7e2t\nXr16ydnZOUqZFy5c0K5du7Ru3Tr99ddfWrRo0RuH3e+++65sbW31/Pnzl2t37tzRmjVr1KBBgyg9\n/r9lzJhRH3zwgXbs2BFufcOGDUqTJo26dOmiVKlSRXrso0ePtHjxYi1ZsuRllbadnZ3RQWdScenS\nJa1YsUKzZs1SvXr1VL16dTk4OLz18RcuXFC/fv0iVOhnyZJFpUuXNrzbqNu8ebO6deumS5cuGctM\nnTq1Bg8erN69e3MmNwAAQBIV78NuAAAAAEDylC5dOn399ddq3bq1unTpot27dxvJ9fb2VqVKldS8\neXNNnDhROXPmNJILRFeKFCk0adIktWnTRoGBgeFu8/LyUrNmzVS8eHFVqFBBRYsWVe7cuZU+fXql\nTJlSjx8/1qNHj3Tr1i2dP39e58+f12+//RZpFfXb7KNKlSoRhtLjx4/XwYMHVaFCBeXJk0dp0qSJ\ncLZ5ypQpXzuQ79ixo/bu3RtukC5JK1as0O7du1WjRg25ubkpY8aMevLkif766y95eXnpwIEDevDg\nwcv7lypVStmzZ9fPP/8c5eeXXNy8eVNz587V3Llz9e6776pEiRJycXGRo6OjMmXKpPTp08vW1lZP\nnz5VYGCgAgICtGfPHu3du1ehoaER8rp27SobG5t4eCZ/u3jxorp3767Nmzcbza1fv76mTp2qd955\nx2guAAAAEhaG3QAAAACAePX/2LvzMJvr/o/jzzP2NUsyltDCjCVLlhZlCcnWvmhR2hclWrRJSdut\nqEh1t97dd/1apJC9SFRUyM6IEllKZCfLnN8fx4hQzpnvzJnl+biuc5n5Op/35z1d1+/+mXnP5/Wp\nUaMG48eP57333uPOO+8M5A5hgP/9738MGzaMRx55hC5duhhtrrg66qijePnll7ntttv46aefDvj7\n7777ju+++y7D+7jkkkv49NNPCYfD+z2fPHnyQeOt05QrV46PP/74kH9fpUoVbrzxRgYOHHjA361e\nvZo333zzH3s79thjefLJJ3n22Wf/8b2KWLJkSbrutG7fvj3t27cPsKPDt23bNv71r3/x5JNPHnDa\nPD2OP/54Bg4cyFlnnRVYTUmSJGVdsV8KJUmSJElSQEKhEB07dmThwoXcfffdgQ2mN27cSLdu3Tjx\nxBP/dpAnZYby5cvz5ptvZsi9wYd7Mrdu3bpcddVVge8PcNVVV3H11VfHtLZ27dq89NJLlChRItim\ndFChUIjLL7+chx56KNP3DofDDB8+nJo1a9K7d+/ABt2FChXiscceY+7cuQ66JUmSchGH3ZIkSZKk\nLKNYsWL07duXWbNmccYZZwRWd86cOTRp0oROnTqxatWqwOpK0SpatCh9+vTh3//+NyeeeGK6aiUm\nJtK5c2c++OADatSocdjrbr31Vu6//36OOOKIdO1/MF26dOHJJ5+kQoUKh/X+IkWK0KVLF15++WVK\nlSoVeD85SevWrTn77LMpXbp0uurUrFmTV199le7duxMKhQLq7vAsWbKE9u3bc8455wR6N/cFF1zA\nwoULuf/++w95P7wkSZJyplD4r7lVClz9+vVZvXo1iYmJTJ8+Pd7tSJIkSVK2EA6Hef/997nzzjtZ\nsWJFYHWLFSvGI488wq233mq0ueLuxx9/ZPz48UybNo2UlBQ2bdp00PcVKFCASpUqccwxx1C3bl0a\nNWpElSpV0rX3jh07mDRpEtOnT2fRokWsWrWKLVu2sH379gPudv6nGPOD1Z48eTJfffUVc+fO5fff\nf2fDhg3kz5+fI488kuOPP57GjRvTsmVLihYtmq6vI7cJh8MsWrSI2bNnM3v2bBYvXsyKFSvYunXr\nQd9ftGhRqlatSp06dWjdujVVq1bN5I5h69atPPnkk/Tt2zfQyPJq1aoxcOBAzjzzzMBqSpIkKXtx\n2J0JHHZLkiRJUuw2b95Mnz596N+/P7t27Qqsbq1atRg0aBBNmjQJrKaUXhs2bGDt2rX88ccfhEIh\nihQpQpEiRShRogQJCQb06dB+//13Nm3atHfoXaRIEYoWLUrJkiXj1lNaZPntt99+0LvqY1W4cGEe\nfPBBunfv7kluSZKkXM5hdyZw2C1JkiRJ6bdgwQJuu+02xo8fH2jdyy+/nKeeeopy5coFWleScrPF\nixfTtWtXRo8eHWjdCy+8kH79+lGpUqVA60qSJCl7yhbD7l27djFt2jRmzpzJwoULWbFiBWvWrGHr\n1q3s3LmTfPnyUbhwYcqUKUOFChVITk6mXr161K9fP0tE0jnsliRJkqRghMNhPvjgA7p37x54tHnv\n3r259dZbyZcvX2B1JSm32bp1K0888QR9+/Zlx44dgdVNSkpi4MCBtGrVKrCakiRJyv6y9LD766+/\n5q233mLcuHEH3Dt0sLZDodB+nxcuXJg2bdpw2WWX0ahRowzt9e847JYkSZKkYG3evJlHH32U/v37\ns3PnzsDq1qxZk0GDBtG0adPAakpSbhAOhxk6dCjdu3cPPLK8V69edO/enfz58wdWV5IkSTlDlhx2\nz507l169evHtt98ChzfY/qf3nXTSSfTp04fq1asH3O0/c9gtSZIkSRlj4cKF3HbbbXz66aeB1r3s\nsst46qmnKF++fKB1JSkn+v7777ntttsYO3ZsoHUvuugi+vXrx9FHHx1oXUmSJOUcCfFu4K+eeeYZ\n2rdvz7fffks4HCYcDhMKhQ54HczB3pdWY+rUqbRp04YBAwZk8lckSZIkScooycnJjBs3jsGDB1Ox\nYsXA6v7f//0fSUlJ9OvXL9CT45KUk2zZsoUHHniAWrVqBTroTk5O5pNPPuH999930C1JkqS/lWWG\n3bt37+amm26if//+7Nq1a78hd3rsW2PXrl089dRT3HrrraSmpgbRtiRJkiQpzkKhEBdeeCELFy7k\n3nvvDezO7c2bN3PXXXdRt25dJk6cGEhNScoJwuEwH374IdWrV+fxxx8P7G7uIkWK8K9//YtZs2bR\nsmXLQGpKkiQpZ8syw+5u3boxYsSIQw65005o73vau3jx4pQtW5bixYvvd4o77bWvfU96Dxs2jDvu\nuCMzvzxJkiRJUgYrUqQITzzxBHPmzKFVq1aB1Z0/fz7NmzfnsssuY+XKlYHVlaTsaNGiRZx11llc\ncMEFLF++PLC6l1xyCQsXLqRHjx7ezS1JkqTDliXu7H7jjTd48MEH//Ye7gYNGtC6dWtq1apFzZo1\nKVWq1AHvXbduHfPmzWPevHmMHTt2753fBxuch0Ih+vTpQ+fOnYP/gv7CO7slSZIkKXOlnTrs3r17\noMOYokWL8tBDD3H77bcHdoJckrKDLVu28Nhjj/H0008Her1D9erVGThwIC1atAispiRJknKPuA+7\nV65cSbNmzdi2bdt+z9MG0pdccgm33norVapUibr2smXLeP7553n33XcPOOkdDocpUqQIEydOpFy5\ncun5Ev6Rw25JkiRJio8tW7bw+OOP89RTTwU6nKlRowbPP/88zZs3D6ymJGVF4XCYIUOGcMcddwT6\ny0NFihTh4YcfpmvXrp7kliRJUsziHmP+/PPPs3Xr1v2ehcNhypUrx7Bhw3j66adjGnQDVKpUib59\n+zJ8+HDKly9/wN9v3bqVQYMGxVRbkiRJkpT1FSlShMcee4y5c+dy5plnBlZ3/vz5nHHGGVx66aWs\nWLEisLqSlJUsWLCAM888k4suuijQQXfHjh1JSUnhrrvuctAtSZKkdInrsHvbtm0MHjx4b8x42unr\n4447jqFDh3LiiScGsk/dunX56KOPOPbYY/c+S7u/+/333z/gVLkkSZIkKWepVq0aY8aMYciQIVSq\nVCmwuu+++y7Jyck89dRT7NixI7C6khRPmzZt4u6776Z27dp8+umngdWtUaMGEyZM4J133qFChQqB\n1ZUkSVLuFddh9/jx4w8YNOfPn59XX3018H/wli9fnldeeeWA3xbdtm0b48ePD3QvSZIkSVLWEwqF\nOP/885k/fz73339/YKcJN2/eTI8ePahTp47fX0rK1sLhMG+//TZJSUk8/fTT7Nq1K5C6RYsW5emn\nn2bmzJle/yBJkqRAxXXYPWXKlL0fp93RfdNNN1G1atUM2a9atWrceOONB9zf/dVXX2XIfpIkSZKk\nrGffaPPWrVsHVnfhwoW0bNmSSy65hJ9//jmwupKUGWbPnk3Tpk254oorWLVqVWB1L7vsMlJSUrjz\nzjvJly9fYHUlSZIkiPOwe/78+Qc869ixY4bueemllx7wbMGCBRm6pyRJkiQp66latSqjR4/mww8/\nDDTa/P333yc5OZm+ffsabS4py1u/fj233347J554IpMnTw6sbs2aNfnss894++23KV++fGB1JUmS\npH3Fddi9bNmyvfd1Q+QHDUcffXSG7nn00UdTrVo14M97u5ctW5ahe0qSJEmSsqZQKMR5553HggUL\neOCBBwKLNt+yZQv33HMPderUCfS+W0kKSmpqKm+88QbVqlVjwIAB7N69O5C6xYoVo3///nz33Xc0\na9YskJqSJEnSocR12L1x40bgzwjzoO/pPpQKFSrsF2W+YcOGTNlXkiRJkpQ1FS5cmEcffZS5c+fS\npk2bwOouXLiQVq1acfHFFxttLinLmD59Oo0bN+aaa65hzZo1gdW9/PLLSUlJoXv37kaWS5IkKVPE\nddj91zi3EiVKZMq+RxxxxH6f79y5M1P2lSRJkiRlbVWrVmXkyJEMHTqUypUrB1Z38ODBJCcn869/\n/ctoc0lxs3btWm6++WYaNmzI1KlTA6tbq1YtPv/8c9566y3KlSsXWF1JkiTpn8R12F2wYMH9Pg/y\nN0n/zm+//bbf5wUKFMiUfSVJkiRJWV8oFOKcc85h/vz5PPjgg4F9z7hlyxbuvfdeateuzSeffBJI\nTUk6HLt37+bf//431apV46WXXtov8TA9ihUrxjPPPMOMGTNo0qRJIDUlSZKkaMR12J12kjvt7uzl\ny5dnyr5/vSu8ZMmSmbKvJEmSJCn7KFy4MI888ghz586lbdu2gdVNSUnhzDPP5KKLLsq074OleFix\nYgUDBgzgqaeeYvHixfFuJ9eaOnUqJ510EjfddBPr1q0LrO6VV17JokWL6Natm5HlkiRJipu4Drsr\nVaq032+SLlu2jPnz52fongsWLGDZsmXAn3eFV6pUKUP3lCRJkiRlX8cffzwjRoxg2LBhVKlSJbC6\nH3zwAcnJyTz55JNGmyvH+eGHH2jUqBG33347PXr0oEGDBsyYMSPebeUqv/76K9dccw2nnHIK06dP\nD6xu3bp1+eKLL3jzzTdJTEwMrK4kSZIUi7gOu2vXrn3As//9738ZuufB6p9wwgkZuqckSZIkKXsL\nhUKcffbZzJ8/n169egUWbb5161buu+8+TjjhBMaNGxdITSkreOmll1i5cuXezzds2ED//v3j2FHu\nsWvXLgYOHEi1atV44403AqtbokQJBg0axLRp02jcuHFgdSVJkqT0iOuwe99/GKdFmb/99tt8++23\nGbLft99+y1tvvbVfhPlf+5AkSZIk6VAKFSpE7969mTdvHu3atQus7qJFi2jdujUXXnjh3jQyKTub\nPXv2Ac9mzpyZ+Y3kMpMnT6Z+/fp07dqVDRs2BFIzFApx3XXXsWjRIm655Rby5MkTSF1JkiQpCHEd\ndjdp0mTvvd0Q+cdzamoq119/feBx5ikpKdx4442kpqbu97xEiRI0bdo00L0kSZIkSTnbcccdx4gR\nIxg+fHig0eZDhgyhevXqPPHEE/zxxx+B1ZUy277X1v3dMwVj1apVXHHFFTRp0uSgv2gQq4YNGzJ1\n6lReeeUVypQpE1hdSZIkKShxHXbnzZuXTp067ffNTigU4rfffuOiiy7i448/DmSfkSNHcsEFF/Dr\nr7/uPdWddl/3lVdeSd68eQPZR5IkSZKUu3To0IH58+fz0EMPBRptfv/993PCCScwevToQGpKypl2\n7txJv379qFatGm+//XZgdUuXLs0rr7zC1KlTadSoUWB1JUmSpKDFddgNcOONN1K6dOn9noVCITZs\n2MAtt9zCJZdcwqRJk6L+7d9wOMykSZO49NJLuemmm1i/fv0B8eWlS5fmhhtuSPfXIEmSJEnKvQoV\nKsTDDz/M/Pnz6dChQ2B1v//+e9q2bcvZZ5/NkiVLAqsrKWcYP348derU4a677mLz5s2B1ExISOCW\nW25h0aJFXHfddSQkxP1Hh5IkSdLfCoWzQIbUxx9/zM0337z33u6/nr4GOOqoo2jevDm1atWiRo0a\nlC5dmmLFilG4cGG2bt3Kpk2bWLduHfPmzWPevHlMmDCBX3/99YA6+37+0ksvBXrH2qHUr1+f1atX\nk5iYyPTp0zN8P0mSJElS/IwYMYKuXbvy448/BlazQIEC3HXXXdx3330UKVIksLpSRmndujXjxo3b\n71mNGjWYN29enDrKOZYvX86dd97J4MGDA6176qmn8vzzz1OvXr1A60qSJEkZKUsMuwGeeOIJBg0a\ndMDp679GnB+uv1sXDofp2rUrPXr0iLHb6DjsliRJkqTcZdu2bfTt25cnn3yS7du3B1b36KOPpl+/\nflx44YVRfY8sZTaH3cH7448/6NevH4899hhbt24NrG7ZsmXp27cvnTp18n9XJEmSlO1kmSyi++67\nj5tvvvmAuPJQKLT3FQ6HD/u177p9hcNhbrvttkwbdEuSJEmScp9ChQrx0EMPMW/evECjzZcvX87F\nF19MixYtHBpKucjo0aOpVasWDzzwQGCD7jx58tC9e3dSUlK48sorHXRLkiQpW8oyw26ABx54gAED\nBlCsWLGD3tG97wD7n15/FQ6HKV68OIMGDeKee+7JjC9HkiRJkpTLHXvssQwfPpwRI0Zw7LHHBlb3\ns88+o06dOnTr1o3169cHVldS1vLjjz9y7rnn0rZtWxYvXhxY3WbNmjFr1iz69+/PEUccEVhdSZIk\nKbNlqWE3wPnnn8/EiRO55JJLyJs3796T2rFIW5s3b14uu+wyPv/8c84555yAO5YkSZIk6e+1a9eO\nefPm0bt3bwoWLBhIzd27d/Pcc89RrVo1Xn/9dVJTUwOpKyn+tm3bxsMPP0yNGjUYNmxYYHUrVKjA\nu+++y4QJE6hZs2ZgdSVJkqR4yXLDboCjjjqKfv368eWXX3LnnXeSnJwcVYR52nC8Ro0a9OjRg6++\n+oq+ffty5JFHxvkrkyRJkiTlVgULFqRXr17Mnz8/0F/EXrNmDddeey2nnHIK33zzTWB1JWW+cDjM\nsGHDqFGjBr1792b79u2B1M2XLx/33HMPCxcu5JJLLjGyXJIkSTlGKBzrselM9ttvvzFz5kxSUlJY\nsWIFa9asYdu2bezYsYP8+fNTqFAhypQpQ4UKFUhKSqJevXqULl063m0DUL9+fVavXk1iYiLTp0+P\ndzuSJEmSpCxg1KhRdO3alSVLlgRa99prr+Xxxx/nqKOOCrSuFI3WrVszbty4/Z7VqFHDu+b/RkpK\nCt26dWPMmDGB1j3zzDMZMGAASUlJgdaVJEmSsoJsM+zOzhx2S5IkSZIOZvv27Tz99NM8/vjjbNu2\nLbC6RxxxBI888gi33HILefPmDayudLgcdh++jRs30qdPH5599ll27doVWN3KlSvzzDPPcO6553qS\nW5IkSTlWXGPMV65cyfz58/d7rVy5Mp4tSZIkSZKUaQoWLEjPnj1ZsGABF154YWB1N2zYwO233069\nevWYOHFiYHUlBSc1NZX//ve/JCUl8fTTTwc26C5QoMDeKxPOO+88B92SJEnK0eI67L799ttp3br1\nfi9PPkuSJEmScpvKlSszePBgPv30U6pXrx5Y3blz59K8eXMuueQSli9fHlhdSekzbdo0GjduzFVX\nXcXq1asDq9uhQwfmzZtH7969KVy4cGB1JUmSpKwqrsPu77//nnA4vPdVpEgRzjrrrHi2JEmSJElS\n3LRo0YJZs2bRv39/ihcvHljd999/n+TkZB577DG2b98eWF1J0fn111+57rrraNSoEVOnTg2s7nHH\nHceIESMYPnw4xx13XGB1JUmSpKwursPu9evXEwqF9r5q1KhBvnz54tmSJEmSJElxlS9fPrp3705K\nSgqdO3cOrO7WrVvp2bMntWrVYsSIEYHVlfTPdu7cyXPPPUe1atV47bXXCIfDgdQtVKgQffr0Ye7c\nubRr1y6QmpIkSVJ2Etdhd9pgO+0f+ImJifFsR5IkSZKkLCMxMZE33niDKVOm0KBBg8DqLlmyhA4d\nOtCuXTu+//77wOpKOrjx48dTt25dunXrxoYNGwKre8EFF7BgwQJ69uxJwYIFA6srSZIkZSdxHXb/\nNZItISGu7UiSJEmSlOWcfPLJfP3117zyyisceeSRgdUdNWoUtWrV4r777mPz5s2B1ZUUsXTpUi64\n4AJatmzJ/PnzA6ublJTEuHHj+OCDD6hcuXJgdSVJkqTsKK7T5cqVKxMOhwmFQgD89ttv8WxHkiRJ\nkqQsKSEhgeuuu45FixZx6623BvbL4jt27ODJJ58kOTmZd999N7BoZSk327p1Kw8//DDVq1fnww8/\nDKxukSJF6Nu3L7Nnz6ZVq1aB1ZUkSZKys7gOu2vUqLH343A4zIoVK+LYjSRJkiRJWVvJkiUZOHAg\n3333HU2aNAms7ooVK7j00ktp1qwZs2fPDqyulJuEw2E++OADqlevTu/evdm+fXtgtTt27EhKSgp3\n3303+fPnD6yuJEmSlN3Fddh9+umn7/f50qVLWb58eZy6kSRJkiQpe6hduzYTJ07knXfeoUKFCoHV\nnTRpEvXq1ePmm29mzZo1gdVVzvHRRx9x/vnnc+GFFzJhwoTA6n777bdcccUVtG/fnjfeeCOwupll\n7ty5tGzZkosuuohly5YFVrdOnTpMmjQp8P9blyRJknKKuA67mzVrRqlSpfZ7NnTo0Pg0I0mSJElS\nNhIKhejYsSMLFy7kvvvuC+y0Z2pqKi+99BLVqlXjueeeY+fOnYHUVfb3wQcfcP755/PRRx8xZMgQ\n2rRpw+TJk9Ndd968ebRs2ZK3336bkSNHcs011zBgwIAAOs54v//+O7fffjt169YNdPhfqlQpXnjh\nBaZPn37AYRFJkiRJf4rrsLtAgQJ07tx5773d4XCYF154gXXr1sWzLUmSJEmSso2iRYvy+OOPM3fu\nXNq2bRtY3fXr19OtWzdq167NmDFjAqur7OuVV17Z7/MdO3bQtWvXdN/13qNHDzZu3Ljfs5dffjld\nNTPa7t27eeWVV6hWrRoDBgxg9+7dgdRNSEjglltuYdGiRdx8883kyZMnkLqSJElSThXXYTfALbfc\nQuXKlYHIb6Vv2rSJG264IdB7jSRJkiRJyumqVq3KyJEj+fjjjznuuOMCq7tw4ULatGlD+/btWbRo\nUWB1lf0ULFjwgGczZ85k2LBhMdf85ptvGDVq1AHPCxUqFHPNjDZx4kQaNGjADTfcwG+//RZY3SZN\nmjBjxgwGDRpE6dKlA6srSZIk5WRxH3YXLFiQ1157jSJFigCRgffXX39Np06dWL16dZy7kyRJkiQp\ne2nfvj1z587lscceo3DhwoHVHTlyJDVr1uTOO+9k/fr1gdVV9tG+ffuDPu/du3fMp7t79+590Oft\n2rWLqV5G+uGHH7jgggto3rw5M2fODKxuhQoVeOedd5g4cSJ16tQJrK4kSZKUG8R92A2QnJzMe++9\nR8mSJQmHw4TDYaZMmULz5s158cUXWbt2bbxblCRJkiQp2yhYsCD3338/Cxcu5OKLLw6s7q5du+jf\nvz/VqlXjlVdeCSy6WdnDVVddRaVKlQ54Huvp7kOd6i5evDi33357TD1mhI0bN3LvvfdSvXp1Pvzw\nw8Dq5s+fnwceeICUlBQ6duxIKBQKrLYkSZKUW4TC6b1YKZ1WrFix9+NVq1Zx3333sWDBgr13eIdC\nIfLmzUvjxo2pW7cutWrVokyZMhQrVmzvafD0qlChQiB1DqV+/fqsXr2axMREpk+fnqF7SZIkSZL0\nV5999hldu3Zl7ty5gdatW7cuzz33HE2aNAm0rrKul19+mRtvvPGA53Xr1mXGjBl7B7atW7dm3Lhx\n+72nRo0azJs3b+/n7dq1O+iwu1evXoc88Z2Zdu/ezX/+8x8eeOABfvnll0Brn3POOfTr1y/QKwck\nSZKk3Cjuw+6KFSse8JuraUPutI+BDPvt1lAoxLJlyzKkdhqH3ZIkSZKkeNu1axcvvPACvXr1YsOG\nDYHWvuiii+jbty9VqlQJtK6ynh07dlC1atWD/izlo48+4txzzwX+edj9zTffcNJJJx1Qo3jx4ixd\nupSSJUsG33wUPv/8c7p37853330XaN2kpCSeffZZzjrrrEDrSpIkSblVlogxT4suT3ulPYPIMDrt\nlHdGvSRJkiRJyuny5s1L165dWbRoEddee22gv1Q+ePBgqlevzoMPPsiWLVsCq6usJy16+2Ciubv7\nUCe3u3XrFtdB948//siFF15Is2bNAh10FytWjKeffprZs2c76JYkSZIClCWG3WkD7bRXmn2H0X99\nTxAvSZIkSZJym6OOOopXX32Vr7/+mpNPPjmwutu3b+fRRx8lKSmJ//3vf6SmpgZWW1lL586d03V3\n99/d1d2tW7cgWozapk2buO+++0hOTmbIkCGB1u7cuTOLFi3izjvvJH/+/IHWliRJknK7LDHs/iuH\n0pIkSZIkZayGDRvy1Vdf8dZbb1G+fPnA6q5YsYIrr7ySRo0aMWnSpMDqKutI7+nurHSqe/fu3bz+\n+utUrVqVJ598kh07dgRWu2HDhkydOpU33niDxMTEwOpKkiRJ+lOWGHZnZES58eWSJEmSJB1cKBTi\n8ssvJyUlhZ49e1KwYMHAak+fPp2mTZty/vnn8/333wdWV1lDrKe7s9Kp7smTJ9OwYUOuvfZafvnl\nl8DqlilThtdee42pU6ce9F5ySZIkScEJheM89X3//ffjuT0AF198cYbWr1+/PqtXryYxMZHp06dn\n6F6SJEmSJMVq6dKl9OjRg8GDBwdaN2/evHTp0oVevXpRqlSpQGsrfl5++WVuvPHGA57XrVuXMmXK\n8Mknn+z3vEaNGlSpUuWgw+5evXod8sR30JYsWcK9997LBx98EGjdvHnz0rVrVx588EFKlCgRaG1J\nkiRJBxf3YXdu4LBbkiRJkpSdfP7559x+++3MmjUr0LolS5bkwQcfpEuXLt5dnAPs2LGDqlWrsmzZ\nsgP+rm7dusycOXO/Z8cccww//vjjAe8tXrw4S5cuzfAI87Vr19KnTx9eeOEFdu7cGWjts88+m6ee\neopq1aoFWleSJEnS38sSMeaSJEmSJCnraNq0KdOnT+fll1+mTJkjA6v7+++/c8cdd1CjRg2GDBni\nFWPZ3N/d3b1kyZIDnq1Zs+ag783ou7q3b99O3759Oe6443juuecCHXTXrFmTcePGMWzYMAfdkiRJ\nUhx4sjsTeLJbkiRJkpRdrV+/nj59+jBgwAB27doVaO3TTjuN/v3707Bhw0DrKvP83enuw5GRp7pT\nU1P5v//7Px544IGY+zuUUqVK8+ijfbj++uvJmzdvoLUlSZIkHb64nuxeuXIl8+fP3++1cuXKeLYk\nSZIkSZL2UaJECfr168fcuXNp165doLW/+OILGjVqxOWXX87SpUsDra3M8Xenuw9HRp3qnjBhAg0b\nNqRTp06BDrrz5MlL9+7dWbz4e26++WYH3ZIkSVKcxfVk90UXXcTUqVP3e/bCCy/QoUOHOHWUMTzZ\nLUmSJEnKKUaPHk33breTsuj7QOvmz5+fLl268MADD1C6dOlAaytjxXq6OyNOdc+bN48ePXowatSo\nwGqmadeuPf379zOuXJIkScpC4nqy+/vvvyccDu99FSlShLPOOiueLUmSJEmSpL/Rpk0b5sydxzPP\nPMMRxYsFVnfHjh0888wzHHvssTzxxBNs3bo1sNrKWLGe7g7yVPeqVau4/vrrqV27duCD7qSkGowd\nO5YRIz520C1JkiRlMXEddq9fv55QKLT3VaNGDfLlyxfPliRJkiRJ0j/Ily8f3bp14/vFS+hyyy3k\nyRPcjxc2btzI/fffT9WqVXnllVcCvydcGaNz585UqlTpsN9fvHhxunXrlu59N2zYQK9evTj++ON5\n9dVXSU1NTXfNNMWLl+L5559n7txZnHnmmYHVlSRJkhScuA670wbbaUnqiYmJ8WxHkiRJkiRFoUyZ\nMjw/aBBz586jQ7s2gdZeuXIlN9xwAyeccAJDhw4ljrew6TBEe7o7vae6t23bxtNPP82xxx5Lnz59\nAk0CSEjIS9eut7N06WK6dOnivdySJElSFhbXYXfx4sX3+zwhIa7tSJIkSZKkGCQnJzN8xCjGjx9P\n3ROSA629cOFCzjvvPE499VQmTJgQaG0F63BPd6fnVPfOnTt5+eWXqVq1KnfffTfr1q2Lqc6htGzZ\nlnnz5vDcc88Gepe4JEmSpIwR1+ly5cqVCYfDhEIhAH777bd4tiNJkiRJktLhjDPOYNp3c3nj9dcp\nd1Swg8KpU6fSokULWrRowZQpUwKtrWAc7unuWE51p6am8u6771KjRg1uvPFGVqxYEWubB1W1ah3G\njh3LJ5+MJDk52F/YkCRJkpRx4jrsrlGjxt6Pw+Fw4N+oSJIkSZKkzJUnTx46X3013/+wnIcfvI/C\nBfMFWn/ChAmceuqptGvXju+++y7Q2kq/fzrdHe2p7nA4zKhRo6hfvz6XXnopixcvDqDLP5UoUYHX\nX/8PCxZM915uSZIkKRuK67D79NNP3+/zpUuXsnz58jh1I0mSJEmSglKkSBEeeuRxvl+ylKsvP489\noW6BGTVqFCeeeCIXXngh8+fPD7a4YvZPp7sP91R3OBxmzJgxnHLKKbRr146ZM2cG2CXky1eMBx54\njBUrFnH11VeRJ0+eQOtLkiRJyhxxHXY3a9aMUqVK7fds6NCh8WlGkiRJkiQFrnz58rz+1ofMmD6D\nFo1rBV5/yJAh1KpViyuuuIKUlJTA6yt6nTt3pkiRIgc8z5Mnzz+e6t53yN2mTRu+/vrrQHsLhfJy\n0UVd+PnnxTz66P0ULlw40PqSJEmSMldch90FChSgc+fOe+/tDofDvPDCC6xbty6ebUmSJEmSpIDV\nrVePTybPZsTQwdQ87shAa4fDYd5++22qV69Ox44dmTNnTqD1FZ38+fNz8803H/D8nHPOOeSp7owe\ncgPUq3ce8+fP4/33n+eoo44KvL4kSZKkzBfXYTfALbfcQuXKlQEIhUJs2rSJG264ge3bt8e5M0mS\nJEmSFKRQKES7cy5kVspq3hj0GBXLFAi0fjgc5r333qN27dqcd955TJ8+PdD6OnxPPfUUnTp1omDB\nguTLl4+zzjqLwYMHH/C+zBhyly17MiNHTmbGjA9JTq4WeH1JkiRJ8RMKh8PheDexcOFCzj33XLZs\n2bL32cknn8zAgQNJTEyMY2fBqF+/PqtXryYxMdFvtCVJkiRJ2mPb1q08/+iNPD7gbdZvyZgfT7Rp\n04aePXty6qmnZkh9xWbXrl18+OGH9O3bN8N+VlKgwHE8/PAT3HPPhYSCvjRekiRJUpYQ95PdAMnJ\nybz33nuULFmScDhMOBxmypQpNG/enBdffJG1a9fGu0VJkiRJkhSwQoULc/fj/+OHH36iR+eTKJAv\n+D1Gjx5N48aNadGiBZ9++ilZ4Hf+c7Vt27bx4osvkpSUxCWXXJIhg+5QqCyXXTaQ9evnc++9Fzno\nliRJknKwuJ/sXrFixd6PV61axX333ceCBQv23uEdCoXImzcvjRs3pm7dutSqVYsyZcpQrFgxihQp\nEkgPFSpUCKTOoXiyW5IkSZKkf7Z83mc8dNflvDl2FakZ9NOKE044gTvuuINLL72UAgWCjVHXoa1b\nt44XXniBAQMGsGbNmgza5QgaNerBBx/cztFHB/MzI0mSJElZW9yH3RUrVjzgN2zThtxpHwMZ9lu4\noVCIZcuWZUjtNA67JUmSJEk6TOEw88c/y0O9HuCDKdsybJvExERuvfVWbrrpJkqXLp1h++R2y5Yt\n49lnn+Xll1/e7/q6YBWiXLnbefvtHjRvXjKD9pAkSZKUFWWJGPO06PK0V9oziAyj0055Z9RLkiRJ\nkiRlEaEQNVp2Z/DnvzLjnc60q5cxv/y+evVqevbsydFHH83NN99MSkpKhuyTG4XDYT799FPOP/98\njjnmGJ555pkMGnTnpWDBW+jXbwk///yEg25JkiQpF8oSw+60gXbaK82+w+i/vieIlyRJkiRJyqLy\nFaVexzcYMXEBXw1oSIuaGbPNtm3beOmll0hOTqZ9+/aMGjWK3bt3Z8xmOdz69et57rnnSE5OplWr\nVnz00UekpqZmwE4JwBVcfnkKK1YM4o47ypGQJX7CJUmSJCmzZclvBRxKS5IkSZIkAIonccqtX/Pp\nqA+Y8EgZTqmacVuNHDmSdu3acfzxx/PEE0/wyy+/ZNxmOcjMmTO54YYbqFChAt26dWPRokUZtFMC\ncDl16sxj+vT/8dZbx1KqVAZtJUmSJClbyBJ3dsdTKBRi+fLlGbqHd3ZLkiRJkhSAXVsIz3mU0e8+\nRe8hu/lmScZulzdvXtq3b8/VV19NmzZtyJcvX8ZumI1s2LCBwYMH8/rrrzNlypQM3i0BuJQSJXrS\nv38yV12FJ7klSZIkAVlg2P3+++/Hc3sALr744gyt77BbkiRJkqQAbUwh/O1tfPrpJ/T5CCZnwnXb\nRx11FFdccQWXX3459erVy5VJdLt27WL8+PG8+eabfPTRR2zfvj2Dd4wMuUOhntxySzJ9+kBJr+WW\nJEmStI+4D7tzA4fdkiRJkiQFLByGnz+C6d2YNH05fYbCp3MzZ+tq1arRsWNHOnbsSPXq1TNn0zjZ\nvXs3kydP5v333+eDDz5gzZo1mbBrZMgNPTnllGQGDYJ69TJhW0mSJEnZjsPuTOCwW5IkSZKkDLJr\nC8x7HBY8zdSUHTw6FEbOzLztq1evzjnnnMM555xDo0aNSMgB+drbt29nwoQJDB8+nOHDh7Nq1apM\n2rkA0Bm4kzJlqtK3L1x5pZHlkiRJkg7NYXcmcNgtSZIkSVIG27gIpneFVWP5bik8NhQ+nBY5AJ5Z\nEhMTOeuss2jVqhUtW7bkqKOOyrzN0yEcDrN48WImTJjAmDFjGDduHFu3bs3EDkoAtwBdSUgoyy23\nwCOPGFkuSZIk6Z857M4EDrslSZIkScoE4TD8PBSmd4Oty1jyCwwYC69NhC1/ZH47derUoVmzZpx6\n6qmceuqpVKxYMfObOIjU1FQWLlzI1KlTmTRpEhMmTGD58uVx6KQCcAdwPVCMU0+FQYOgbt04tCJJ\nkiQpW3LYnQkcdkuSJEmSlIl2bd0Tbf4UpO5g/RZ45bPI4PvndfFr6+ijj6ZBgwbUqVOH2rVrU7t2\nbY455pgMjT7fvn07CxcuZN68ecydO5fp06fz9ddfs3Hjxgzb85/VAHoQuZc7P2XKwFNPQadORpZL\nkiRJio7D7kzgsFuSJEmSpDjY+P2eaPMxAOzcBR98A/1GwfQf49zbHvnz56dKlSoce+yxHHfccVSo\nUIEyZcrsfR1xxBEULFiQQoUKUbBgQQB27tzJjh072LlzJ5s2bWLdunWsW7eOtWvXsmrVKpYuXcpP\nP/3ETz/9xNKlS0lNTY3zVwmQAHQgElfeEkggIQG6dIlElpcoEdfmJEmSJGVTDrszgcNuSZIkSZLi\nJByGn4fB9Nth67K9j75IgefGwNDpsDsrzIJzrDJEYspvBCrtfdq4MTz/vJHlkiRJktInb7wbkCRJ\nkiRJyjChEBx9LpQ7E+Y9AQv6EkrdwenJcHoyrPw9cqf3yxPiG3Ge8zQmcor7AqDA3qdHHfVnZHko\nFK/eJEmSJOUU2eJk9y+//MI333zDtGnTWLlyJevXr2f9+vVs2bKFcDhMKBTiq6++inebh+TJbkmS\nJEmSsoiN30dOea8avd/jXbth9Cx4/XMY8V3kc0WrONARuBmou9/fJCTArbdC795GlkuSJEkKTpY9\n2b1t2zbee+89/vOf/7BkyZID/n7fGX3oMH4VeMyYMXz++ef7PTvttNNo165d+puVJEmSJEnZQ/Gq\n0GwkrBgeGXpv+QmAvHmgw4mR168b4K0v4Y3PYe7Pce43ywsBrYCrgHOBwge847TTIpHldepkbmeS\nJEmScr4sebL75ZdfZsCAAWzYsIG/ay8UCu092b18+fK/rblgwQJatWq132D8mGOOYdKkSYH1fSie\n7JYkSZIkKQvatRXmPwnz+0LqHwf8dTgMs5fBu1Pg3amwdE0cesyyGgAXA5cCFQ/6jrJlI5HlV1xh\nZLkkSZKkjJGlht2//fYbt99+O5MmTdo75P6nU9uHO+wG6NixI1988cV+Q/Jhw4Zx4oknBtL/oTjs\nliRJkiQpC9u0OHLKe+WoQ74lHIavF8N7U2Ho9Nw6+K5LZMB9MXDcId+VkAC33RaJLD/iiExqTZIk\nSVKulBDvBtL88MMPnHXWWXsH3aFQ6IBBdzgc3u8VrauvvvqAZ0OHDo21ZUmSJEmSlBMUOx6ajoAm\nw6BIlYO+JRSCk6vCM53gh2dg1hPwyIVQ/5jMbTVz5QfOAgYBPwHfAffxd4Pu006D776DZ5910C1J\nkiQp42WJO7vXrVvHpZdeyurVq4H9T3OnDbWLFClC9erVKVWqFCkpKfz0009R79OsWTOKFCnC1q1b\n957uzowYc0mSJEmSlMWFQlDxbEhstSfa/F8HjTZPe2vtSpHXg+fBLxtg/Fz4ZC58MgdW/J7JvQeq\nNnAG0AJoBhQ9rFVly8LTT8PllxtZLkmSJCnzZIlhd7du3VixYsUBQ+48efLQrl07rr76ak488UTy\n5MkDQPfu3WMadhcoUIDmzZszYsSIvXstWbKEX375hbJlywbzxUiSJEmSpOwrbyGo3RuOuXJPtPnI\nf1xS9gi4rHHkFQ7D96vhqx8K8eWaunw1bwPz58/PhMajlz9/furUqc/OnScza9bJhMPNgKOiqpEn\nTySy/OGHPcktSZIkKfPFfdg9duxYJkyYcMCgu2LFirz00kvUrVs30P1atGjBiBEj9ns2depUzjnn\nnED3kSRJkiRJ2Vix46DZCPj5Y5jeFbYsPaxloRBUKwfVym2jM1Ogc21+P34UM1cUZPbs2Xtf8+bN\nY9u2bRn7NeyjdOnSnHDCCdSqVYtatWpRu3Zd5s2rywMPFODXX2OrefrpMGgQnHBCsL1KkiRJ0uGK\n+7D72Wef3e/zcDhMlSpVGD58OKVKlQp8v9q1ax/wLCUlJfB9JEmSJElSDlCxAyS2jMSaz3/ykNHm\nh7R+NiWntaX5MVfS/Ia+UOh2IPLzj9WrV/PDDz/www8/sGTJElatWsWaNWv2vtauXcv27dvZvn07\nu3btOqB0njx5KFCgACVLlqR06dKUKlWK0qVLk5iYSJUqVahcuTKVK1emSpUqlClTZu9Bg5kzoUsX\n+Oqr2P6TJCZGIssvu8zIckmSJEnxFddh94IFC5gzZ87eb7bC4TAFChTgv//9b4YMugGOP/54ChQo\nwI4dO/Y+W7JkSYbsJUmSJEmScoC8haD2w3BMJ5jeDVaO+KcVB/rxv/DzUKjdB6reQighL+XKlaNc\nuXI0btz4H5fv2rWL7du3A5AvXz7y5ctHQkJCVC2sXw8PPggvvACpqdF/CXnyQNeukcjy4sWjXy9J\nkiRJQYvuu6KAffrpp3s/DofDhEIhOnfuzLHHHpthe+bJk4djjz12737hcJgff/wxw/aTJEmSJEk5\nRLHjoNnH0GQ4FDkm+vU7N0buAR9TH36dHNXSvHnzUrRoUYoWLUqBAgWiGnSnpsIbb0C1avD887EN\nups0iZwI79/fQbckSZKkrCOuw+7p06cf8OzKK6/M8H1LlCix3+fr16/P8D0lSZIkSVIOUbEDtJsH\nJzwMeQpGv379bPi0CXx1JWxbHXh7+/ruOzjtNLjmGlizJvr1iYnw9tswcSLUqhV4e5IkSZKULnEd\ndv/www97I8wBKlWqROXKlTN83+J/+RXkLVu2ZPiekiRJkiQpB8lbCE54KDL0rtAhthpL/wcjkmDh\ns5B64J3c6fH773DrrdCgAUyZEv36PHngjjsgJcW7uSVJkiRlXXEddq/Z8yvFaZHiVapUyZR9ixQp\nst/nDrslSZIkSVJMih4LTYdD048jH0dr50aY0R3GnAi/Tkp3O2mR5UlJMGhQbJHlTZtGIsv79TOy\nXJIkSVLWFtdh99atW/f7vFSpUpmy71+H23ny5MmUfSVJkiRJUg5Vof2eaPPeMUabz4FPm8JXnWDb\nqphamDEDGjeOPbK8XDn4v/+Dzz4zslySJElS9hDXYXfevHn3+3zbtm2Zsu9f7+guWDCGb0IlSZIk\nSZL2lacgnNAL2s2HCmfHVmPpW/BxdNHmv/8OXbpAw4YwdWr0W+bJA3feCQsXwqWXGlkuSZIkKfuI\n67C7aNGi+33++++/Z8q+y5Yt2++u8KOOOipT9pUkSZIkSblA0WOg6TBoOiK2aPNdmyLR5qPr/W20\neWoqvP46VKsGL7wQW2R5s2YwaxY8/bSR5ZIkSZKyn7gOuytUqLD3vu5wOMzChQszfM8VK1awalUk\nDixt76OPPjrD95UkSZIkSblMhXZ7os0fiS3afMPcPdHmVxwQbT5jBpx6Klx7Lfz2W/Sly5eHd96B\nCROgZs3o10uSJElSVhDXYfdxxx233+cbN25k3rx5GbrnpEkH/kZ0LS+ikiRJkiRJGSFPQTjhwUi0\necVzYqux9O090ebPsO63ndxyCzRoAF9/HX2pvHnhrrsikeUdOxpZLkmSJCl7i+uwu379+gc8e++9\n9zJ0z9dff/2AZ40aNcrQPSVJkiRJUi5X9BhoMhSajoSix/3j2w+waxPMuINf3qzHvM8+JxyOvkTz\n5pHI8qeegmLFol8vSZIkSVlNXIfdLVq02PtxWpT5u+++y6+//poh+40ZM4YFCxbsd193kSJFaNy4\ncYbsJ0mSJEmStJ8KbaHdXKjdB/IUinp59XLz+PzBZrx1y+WUK7HysNaULw/vvgvjx0ONGlFvKUmS\nJElZVlyH3UcffTT169cnvM+vI2/dupUuXbrs9ywIq1at4u6779476E67r/vss88mX758ge4lSZIk\nSZJ0SHkKQq2ee6LNz42pxOWN/4+Up5Po3qY/efPsPOh78uaFu++ORJZfcomR5ZIkSZJynrgOuwFu\nvPHGvR+nDaKnTp1K165d2bnz4N+sRWvlypV06tSJ33//fb/nCQkJXHfddYHsIUmSJEmSFJWiVaDJ\nR9BsFBQ9PurlxQptpv8Vd/LdY/VoWn3ifn93xhmRyPK+fY0slyRJkpRzxX3Y3bZt2/3u7k6LMx86\ndCgXXXQR8+fPT1f9MWPG0K5dO1JSUg441X3RRRdRrVq1dNWXJEmSJElKl/JtoN0cqP0ou0PRR5vX\nOnoeE3s25+0ul3Fi9ZW89x58+qmR5ZIkSZJyvrgPuwGeeuopChX685u5tIH3tGnTaNOmDddffz0j\nRoxg8+bNh1Vv8eLF/Oc//+HMM8/k+uuvZ82aNQfEopctW5aePXsG+nVIkiRJkiTFYu36gtz0/AMc\n13UBH357Xkw1Ljv1HaY9lMTFJ/QjFA4mLU+SJEmSsrJQOOjLsWP08ccfH3BXd9rHoX0ulUpMTGTn\nzp389ttve4fioVCIunXrsn79etauXcumTZsOuT4cDlOgQAHeffddGjZsmBlfGvXr12f16tUkJiYy\nffr0TNlTkiRJkiRlfamp8NprcO+9sG7dn89b1x7DwKtuo2ri4tgKH1EDGjwPZZsH06gkSZIkZUFZ\nZtgN8O6773LPPfeQmpq63/O/tpg25P6nZ2nP962TP39+XnzxRVq3bh1g53/PYbckSZIkSfqrb7+F\nLl0ifx5M/rx/cGfbfvQ891EKF9gW2yaVO0K9p6FwhdgblSRJkqQsKkvEmKfp2LEjb7zxBsWLF99v\ncB0KhfZ7HWyonXbC+6+vff++ZMmS/O9//8vUQbckSZIkSdK+1q6FG2+Ek0469KAbYMeuAjwx/H6q\n91jAkG/Oj22zn96FEcmw4GlINdpckiRJUs6SpYbdAGeccQYTJ06kXbt2hMPhfzyt/XfPgL01Wrdu\nzaeffkrjxo0D71mSJEmSJOmf7N4NL78M1apF/jzcrL1lv1XmwueG0PrJMfy8oWr0G+/aDN/dDaPq\nwOoJ0a+XJEmSpCwqyw27AcqUKcO///1vRo8ezXnnnUf+/Pn3Dq33vYf7YCe44c8BdygUomXLlnzw\nwQe89tprlC1bNh5fjiRJkiRJyuW++QZOPjlyonvfu7kPV8WKcH2v1lS4fg7UeRzyFI6+yMYFMKEF\nfNERtq6Ifr0kSZIkZTFZ6s7uQ9myZQuff/45U6ZMYc6cOfz444+sXbv2gPcVLFiQSpUqUatWLU46\n6STOPPNMypQpE4eO9+ed3ZIkSZIk5U6//Qb33w+vvnr4J7n3lS8f3HknPPAAFC26z19sWQYz7oDl\nQ2JrLG8RqPUQJN0OefLHVkOSJEmS4ixbDLsPZseOHWzevJnt27eTJ08eChcuTLFixeLd1kE57JYk\nSZIkKXfZvTsy4L7//thOcgO0agUDB0JS0t+8adU4mHYbbFoU2ybFk6HB85DYIrb1kiRJkhRHWTLG\n/HDkz5+fUqVKUb58ecqWLZtlB92SJEmSJCl3+eYbOOkkuOmm2AbdRx8NH3wAY8f+w6AboNyZ0HY2\n1HkixmjzhTChJXxxCWz9Ofr1kiRJkhRH2XbYLUmSJEmSlJX89htcf33kbu5Ygt3y5YP77oMFC+CC\nCyAUOsyFeQpAzXuh/QI4+sLoNwZY9j6MSIb5fWH3jthqSJIkSVImc9gtSZIkSZKUDrt3w0svQbVq\nsd/NfeaZMGcOPP44FCkSYyNFKsHpg6H5OCj+T0fCD2LXFph5D4yuA6s/jbEJSZIkSco8DrslSZIk\nSZJi9PXX0KgR3Hwz/P579OuPPhqGDIExYw4jsvxwlWsFbWZD3SfTEW3eCr64GLYsD6gpSZIkSQqe\nw25JkiRJkqQorVkD110XiSyfMSP69fnzw/33RyLLzz8/isjyw5UnP9S4B9ovhEoXxVZj2eA90eb/\nMtpckiRJUpbksFuSJEmSJOkw7d4NL74YOYX92mux1WjdOhJZ/thj6YgsP1xFjobT3oczPokt2nz3\nVph5L4yuDas+Cb4/SZIkSUoHh92SJEmSJEmHYerUSGT5LbfEFlleqRJ8+CGMHh253ztTJbbcE23+\nL8gbw4R9Ywp8diZMvshoc0mSJElZhsNuSZIkSZKkv7FmDVx7LZxySuyR5Q88EIksP++8DIgsP1x5\n8kONHnuizS+OrcbyDyLR5vOeNNpckiRJUtw57JYkSZIkSTqI3bvhhRcip7Bffz22GmedBXPnwqOP\nQuHCwfYXs8IV4bT34IxPoXhy9Ot3b4VZ98GoE2DVuOD7kyRJkqTD5LBbkiRJkiTpL6ZMgYYNoUsX\nWL8++vWVKsFHH8GoUVC1auDtBSOxBbSZBXX7xhZtvmkRfNYaJl8IW5YF358kSZIk/QOH3ZIkSZIk\nSXv8+itccw2ceip891306/Pnh549I5Hl554bx8jyw5UnP9S4e0+0+SWx1Vg+BEZUh3lPwO4/gu1P\nkiRJkv6Gw25JkiRJkpTr7d4NgwZBUhK88UZsNdq0iUSW9+mThSLLD1fhinDau3DGeChePfr1u7fC\nrPsj0eYrxwbfnyRJkiQdhMNuSZIkSZKUq331FTRoALfeGltkeeXKMHQojByZhSPLD1fiGdBmJtR7\nKsZo8+9h4lkw+QKjzSVJkiRlOIfdkiRJkiQpV/r1V7j6amjcGGbOjH59gQLw4IMwfz6cc042iCw/\nXHnyQ/W7oH0KVO4YW43lH8KIZJj3uNHmkiRJkjKMw25JkiRJkpSr7NoFzz8P1arBf/4TW422bSOR\n5Y88kg0jyw9X4QrQ+B1oMSHGaPNtMOuBPdHmY4LvT5IkSVKu57BbkiRJkiTlGl9+GYksv+022LAh\n+vVVqsCwYTBiBBx/fODtZU1lm0PbWVDvachbNPr1m76HiW1g0vmw5afg+5MkSZKUaznsliRJkiRJ\nOd4vv0DnznDaaTBrVvTrCxSAXr0ikeVnn52DIssPV0I+qH7nnmjzS2Or8fNHMKI6zH3MaHNJkiRJ\ngXDYLUmSJEmScqxdu2DgQEhKgjffjK1G27Ywbx707g2FCgXbX7ZTuDw0/j9o8RkcUSP69bu3weye\nMLIWrBwdfH+SJEmSchWH3ZIkSZIkKUf64guoXx+6dk1/ZPlxxwXeXvZWthm0mQn1+sUWbb55MUxs\nC5POg81LA25OkiRJUm7hsFuSJEmSJOUov/wCV10Fp58Os2dHv75AAXjooVwcWX64EvJB9Tv2RJtf\nFluNn4fCyOow91HYvT3Q9iRJkiTlfA67JUmSJElSjrBrFwwYANWqwX//G1uN9u0jkeUPP2xk+WEr\nXB4av70n2rxm9Ot3b4fZDxptLkmSJClqDrslSZIkSVK2N3lyJLL89tth48bo1x9zDAwfDh9/bGR5\nzMo2gzbfwYn9IW+x6NdvXrIn2vxco80lSZIkHRaH3ZIkSZIkKdtavRquvBKaNIktsrxgwcgp7nnz\noEOHwNvLfRLyQXJ36JACVS6PrcbPwyLR5nP6GG0uSZIk6W857JYkSZIkSdnOrl3w3HOQlAT/+19s\nNTp0iAy5H3rIyPLAFSoHp74FLSbCEbWiX797O8zpFYk2XzEy6O4kSZIk5RAOuyVJkiRJUrYyeTKc\neCJ06xZbZPmxx0biyocPj3ysDFS2KbSZASc+E3u0+eft4fNzYPOPwfcnSZIkKVtz2C1JkiRJkrKF\nVaugU6dIZPmcOdGvL1gQeveOnOZu3z74/nQICfkgudueaPMrYquxYjiMrAFzHjHaXJIkSdJeDrsl\nSZIkSVKWtmsXPPtsJLL8rbdiq3H22TB/PvTqFRl6Kw4KlYNT/wctP4cSJ0S/fvd2mPMQjKwJK0YE\n358kSZKkbCdvvBvo168fK1asyNQ98+TJQ/78+SlSpAhHHnkk5cuXJykpieOPP55QKJSpvUiSJEmS\npEObNAm6dIG5c2Nbf+yxMGAAtGsXbF9Kh6OawFkzYNGgyL3cO6PMot/8A3zeASp0gPrPQlGz6CVJ\nkqTcKu7D7rFjx7JgwYJ4twFA0aJFOemkk2jfvj3t2rWjUKFC8W5JkiRJkqRcadUquPtuePvt2NYX\nLAj33x+p4UnuLCghLyTfDpUvge96wNL/RV9jxcewahzUvA+q94C8/hxHkiRJym2yRIx5OBzOEq9N\nmzYxfvx4unfvTqNGjRg4cCA7d+6M938eSZIkSZJyjZ074ZlnIpHlsQ66zzknEln+4IMOurO8Qolw\n6n+h5aTYos1T/4A5DxttLkmSJOVSWWLYHQqFsswrbfD9+++/07dvX1q1asWiRYvi/Z9IkiRJkqQc\n7/PPoV49uOMO2LQp+vXHHQcjR8LQoXDMMYG3p4x01OmRaPP6z0G+4tGv3/JjJNp8YodIzLkkSZKk\nXCFLDLv3dbAT15lZ76+D78WLF3P22Wczffr0dPUhSZIkSZIObuVKuPxyaNYM5s2Lfn2hQtCnT+Re\n77ZtA29PmSUhLyR1hfYpcMyVsdVYOQJG1IDZD8OubUF2J0mSJCkLivuwu2zZslSoUGHvq2LFiuTL\nl2+/oTMcOLROSEigePHiJCYmUrx4cRISEg461N63Rv78+alYsSIVKlQgMTGRwoUL/+0gPG3t5s2b\nufLKK1mxYkXm/seRJEmSJCkH27kT+vePRJb/3//FVuPccyOR5T17GlmeYxRKhFPehJaToUTt6Nen\n/gFze0eizX/+OPj+JEmSJGUZoXB6j04HaMuWLTz88MO88847+w25Q6EQJ510EmeeeSY1a9akRo0a\nlCxZ8oD169evZ/78+cybN4+xY8fy9ddf712f9uell17Kww8/TOHChQHYvXs3S5YsYfr06YwfP55x\n48aRmpq635q0Pk466SSGDBkS9ddVv359Vq9eTWJioifEJUmSJEkCJk6EW2+N7SQ3wPHHw4AB0KZN\noG0pq0ndBd+/CLN7ws6NsdUo3y4Sj17suGB7kyRJkhR3WWbYvWrVKjp16kRKSsp+zy+++GLuuOMO\nKlSoEHXNFStW0K9fPwYPHgz8OTivXr06//3vf0lMTDxgzU8//cTDDz/MJ598st/AO+3Pl19+mTZR\nfiftsFuSJEmSpIiVK+Guu+Cdd2JbX6gQPPAA3HmnJ7lzlW2/wMx74Mc3Y1ufUABq3AM17oW8hYLt\nTZIkSVLcZIlh9/r16znnnHNYsmTJ3melSpXitddeo2HDhumu/+2333Lttdfy+++/740qr1atGh99\n9BFHHHHEQdc888wz9OvXb7+T3QANGzbko48+imp/h92SJEmSpNxu587ISeyHH4bNm2Orcd558Mwz\nULlyoK0pO1nzJXzbBdbPim19kSqRU94VOsCen/lIkiRJyr7ifmc3wN13382SJUv2DpaPPPJIhgwZ\nEsigGyID6g8++IDSpUvv3eP777+nR48eh1zTvXt3Lrnkkv3u/gaYNm2ad3dLkiRJkhSFzz6DunUj\nJ7pjGXQffzyMHg0ffuigO9cr0xjOmgb1B0K+gx9g+FtblsKkc+Dz9rBpceDtSZIkScpccR92T5o0\nidGjR+8XFd6nTx+qVq0a6D7VqlWjT58++8WSjxo1ismTJx9yzaOPPnrQu8EnTJgQaG+SJEmSJOVE\nK1bApZfCGWfA/PnRry9UCB57DObOhbPOCr4/ZVMJeSHpVmifAsd2jq3GylEwsibM7gW7tgbaniRJ\nkqTME/dh97///e+9H4dCIRo0aECHDh0yZK8OHTrQoEGDvQNvgJdeeumQ7y9UqBBXXXUVf016nzlz\nZob0J0mSJElSTrBzJzz9NCQnw7vvxlbj/PNhwQK4/34oUCDY/pRDFCoLJ78Brb6EknWjX5+6A+b2\ngZE14OdhEP+b/iRJkiRFKa7D7vXr1/PFF1/sPWkNcM4552Tonueee+7ej8PhMF9++SXr168/5PsP\nNnj//vvvM6AzSZIkSZKyvwkToE4duPvu2CLLq1aFMWNgyBAjy3WYypwKradBg+djjDb/CSadCxPb\nGW0uSZIkZTNxHXZ//fXX7N69e79np5xySobu+df6u3fv5ptvvjnk+5OSkjjiiMg3SmlD+VWrVmVo\nj5IkSZIkZTcrVkDHjtCiReREdrQKFYLHH4c5c6B16+D7Uw6XkAeqdYEOi+DYq2OrsWp0JNp81oNG\nm0uSJEnZRFyH3YsWLTrgWdmyZTN0z4PVT0lJ+ds11apV2y/KfMOGDYH3JUmSJElSdrRjBzz1FCQl\nwXvvxVbjggtg4UK47z4jy5VOBY+Ck1+HVl/FHm0+79FItPnyoUabS5IkSVlcXIfda9asOeBZkSJF\nMnTPwoULH1Yf+0o72Z3mjz/+CLQnSZIkSZKyo/HjI5HlPXrAli3Rr69WDcaOhQ8+gEqVgu9PuViZ\nU/ZEmw+CfCWiX7/lJ5h8HkxsCxu9zk6SJEnKquI67N62bdsBz3799dcM3fNgg+3t27f/7ZpixYrt\n93nevHkD7UmSJEmSpOzk55/hkkugZcvIiexoFS4MTzwBs2fDmWcG358E7Ik2vwU6pMCx18RWY9UY\nGFULZvU02lySJEnKguI67C5wkGyyH374IUP3PFj9/Pnz/+2avw7DCxYsGGhPkiRJkiRlBzt2QN++\nkJwM778fW40LL4zc6X3vvUaWK5MUPApOfm1PtHm96Nen7oB5j8GI6rD8I6PNJUmSpCwkrsPuMmXK\nHPBszJgxGbrnweofrI99bdq0ab/PMzpqXZIkSZKkrObTTyOR5ffcE1tkeVISjBsHgwcbWa44KXMK\ntP4WGr4QW7T51mUw+XyY2AY2Lgq8PUmSJEnRi+uwOykpae/HoVCIcDjMsGHDWLduXYbst27dOoYO\nHUooFDpkHwezcuXKvWtCoRCJiYkZ0p8kSZIkSVnNzz/DxRdDq1axR5Y/+WQksrxVq+D7k6KSkAeq\n3gwdFsFx18ZWY9VYGHUCzHoAdsXwmx+SJEmSAhPXYffJJ59MQsL+LWzYsIEHH3wwQ/br2bMnGzZs\n2O9ZQkICJ5988iHXbNu2jaVLlwIQ3hNTVbFixQzpT5IkSZKkrGLHDvjXvyKR5YMHx1bjoosiA/J7\n7oF/uEFMylwFy8BJr8KZU6DkidGvT90B8x7fE23+odHmkiRJUpzEddhdokQJmjZtuneInHa6e/jw\n4fTq1SvQvXr16sXw4cP3ntAOh8OEQiGaNm1KiRIlDrlu9uzZpKam7vfsuOOOC7Q3SZIkSZKykk8+\ngdq1I/dqxxpZ/sknkXu9jz46+P6kwBx5MrT+Bhq+CPlLRr9+63KYfAF8dpbR5pIkSVIcxHXYDXDT\nTTft/ThtAB0Oh3njjTfo1KkTP/30U7rqL1u2jE6dOvHGG28c9O9vvvnmv10/bty4A56deGIMv/Er\nSZIkSVIWt3x55DT2mWdCSkr064sUiZwGnz0bWrYMvj8pQyTkgao3QftFcNx1sdVYPQ5G1YKZ9xtt\nLkmSJGWiuA+7GzduTNu2bfcbdKf9OXHiRM444wx69OjB1KlTo6o7depUevToQfPmzZk4ceLeuvDn\nUL1Nmzaccsopf1tn1KhR+93xHQqFHHZLkiRJknKUHTsi92onJ8MHH8RW4+KLI5HlPXoYWa5squCR\ncNIrcOZUKFU/+vWpO2H+E5Fo82VDjDaXJEmSMkEoHI7/v7zXr19P27ZtWb58ObD/CW9g77C5ePHi\n1KhRgxo1anDkkUdStGhRChcuzLZt29i0aRO//fYb8+fPZ/78+WzcuHFvrX1rpD2rXLkyI0eO/NsI\n80mTJnHZZZftt/bEE09k2LBhUX199evXZ/Xq1SQmJjJ9+vSo1kqSJEmSlJHGjYPbboNFMSYwJyfD\n889DixbB9iXFVepuWPIqzLoPdvweW43EVtBgIBRPCrY3SZIkSXvljXcDELm7++233+aiiy5i9erV\ne4fL+57EBtiwYQNTp079x1Pe+87v9x1Up/1duXLlePvtt/920A3w73//+4B67dq1O7wvSpIkSZKk\nLGzZMrjjDhgyJLb1RYrAQw/B7bd7kls5UEIeqHojHH0BzLo/MvgmyvMiqz+BUSdA8p1QqyfkLZIh\nrUqSJEm5WZY42Z1m1apV3HjjjcyYMeOAIXWaw2n379bWr1+fl156iXLlyv1jnalTpx6wX61atShW\nrNg/rt2XJ7slSZIkSVnFH39A//7w6KOwdWtsNS65BJ5+GipWDLY3Kcv67RuY1gXWTYttfeGKcOIz\nkeH5IX5uJUmSJCl6WWrYDZGB9GuvvUbfvn3ZunXrIQfX0dYsXLgw99xzD9dcc00gNaPhsFuSJEmS\nlBWMHRuJLP/++9jWV68OAwcaWa5cKnU3/PAazLwPdqyLrUZiS6g/EI5IDrY3SZIkKZfKcsPuNKtX\nr+att97i3XffZfXq1XufH86get8vKTExkUsvvZTLL7+cxMTEDOn1nzjsliRJkiTF07Jl0L07fPhh\nbOuLFIGHH4auXY0sl/hjbSTafPErRB1tDpCQD5LvgJo9IV/RwNuTJEmScpMsO+xOk5qayueff87X\nX3/NzJkzmTVrFps2bTrk+4sVK0bt2rWpV68eJ510Ek2bNiUhISETOz6Qw25JkiRJUjz88Qf06xeJ\nLN+2LbYaHTtGIssrVAi2NynbW/stfHtLOqPN+8PRFxptLkmSJMUoyw+7D2bTpk1s2LCBDRs2sHXr\nVgoXLswRRxxB8eLFKV68eLzbO4DDbkmSJElSZhszJnISOz2R5YMGQfPmwfYl5ShBRJuXbQENnjfa\nXJIkSYpBthx2ZzcOuyVJkiRJmeWnnyKR5R99FNv6okX/jCzPly/Q1qSc64+1MOsBWPwyMUebJ3WH\nWg8abS5JkiRFIb753pIkSZIkKRB//AGPPRY5kR3roPvSS2HhQrjzTgfdUlQKlIZGL0Hrb6BUw+jX\np+6EBX1hRDL89D54NkWSJEk6LA67JUmSJEnK5saMgVq1oGfP2O7mrlEDPvsM/u//vJtbSpfSDaD1\nVGj0SmQAHq1tK+DLS2BCS9iwIPj+JEmSpBzGYbckSZIkSdnU0qVw3nnQpg0sXhz9+qJFoV8/mDkT\nmjULuDkptwolwPHXQfsUOP4mIBR9jV8mwKja8F0P2Lkp8BYlSZKknMJhtyRJkiRJ2cz27fDoo5ET\n2UOHxlbjsssgJQXuuMPIcilDFCgNjV6MRJuXbhT9+vAuWPDUnmjz94w2lyRJkg4iWw+7w+Ewf/zx\nB2H/sS9JkiRJyiVGj45Elj/4YGyR5TVrRiLL334bypcPvj9Jf1G6AZw5BU56NcZo85XwZcc90ebz\ng+9PkiRJysbyxruBw7F69WomT57MzJkzSUlJYcWKFfz666/s2LFj73vy58/PUUcdRYUKFUhOTqZu\n3bqcfvrplC1bNo6dS5IkSZIUjKVLoVs3GDYstvXFisHDD8Ntt3mSW8p0oQQ47lqoeB7M7gnfvwRE\neXjjlwkwqg4kd4NavSBfsYzoVJIkScpWQuEseiw6NTWVDz/8kLfffptp06bt93d/13IotP89SI0a\nNeLyyy/n3HPPJSEhPgfZ69evz+rVq0lMTGT69Olx6UGSJEmSlD1t3w5PPQWPPx75OBaXXx6pUa5c\nsL1JitG66fBtF1j7dWzrC5WHev2g8iUQiuFOcEmSJCmHyJLD7k8++YSHHnqI5cuXAwcOt/860N7X\nod5buXJlevfuTYsWLQLu9p857JYkSZIkxWLkSLj9dliyJLb1tWrB889D06bB9iUpAOFU+OENmHkv\n/PFbbDXKNof6A6FEzWB7kyRJkrKJLHVn944dO7jjjju45pprWLZsGeFwmHA4TCgU2u/1d/763rQa\nS5cupXPnzvTo0WO/+HNJkiRJkrKaH3+Ec86B9u1jG3QXKwbPPAMzZjjolrKstGjz9ilQ9RYghhPa\nv3wGo+vCjLtg56agO5QkSZKyvCwz7N6yZQsdO3Zk8ODBBwy4DyVtkP1Pseb7Dr7feecdLr/8crZt\n25YRX4YkSZIkSTHbvh0eeQRq1IDhw2OrccUVkJISud/bu7mlbKBAKWg4CM6aBqVPjn59eBcs7Acj\nkmDpO5D1QhwlSZKkDJMlYsxTU1O57LLL+OKLL4CDx5Tv22aRIkUoXbo0xYoVo3DhwmzdupVNmzax\ndu1atmzZsvd9h6oTCoVo0qQJb7311j+eFA+CMeaSJEmSpH8yciR07Qo//BDb+hNOiESWN2kSbF+S\nMlE4FX54E2b2iD3a/Kim0GCQ0eaSJEnKFbLEsLtv374MGDBg7+A5bSCd9nHBggVp06YNZ555Jiec\ncAJVqlQ5ZK2lS5cyd+5cxo4dy5gxY9i2bdsBddP+7NatG3feeWeGf30OuyVJkiRJh/Ljj5F7uT/+\nOLb1xYtHToN36QJ58wbbm6Q42fE7zHoQFr8YGYBHK5QHkm6HEx6CfMWD70+SJEnKIuI+7F68eDGt\nWrVi165d+z1PG3LfeuutXH/99RQpUiTq2lu3buXVV19l4MCBbN++/YD6+fPnZ9y4cRx//PHp+hr+\nicNuSZIkSdJfbdsGffvCk09G4stj0alTpEZiYrC9Scoi1n0H07rAb1NiW1+oHNR7GipfCpmQbihJ\nkiRltrjf2f3cc8+xc+fOvZ+n3cFdvXp1Jk6cSLdu3WIadAMULlyYrl27MnHiRGrUqHHA3d47d+5k\nwIAB6epfkiRJkqRojRgBNWvCww/HNug+4QSYNAn++18H3VKOVqoetPoCTn4DCpSJfv22VfDV5TC+\nOayfG3x/kiRJUpzFddi9YcMGRowYcUDMeP369RkyZAgVK1YMZJ8KFSowZMgQ6tevv3fgnRZnPmLE\nCDZs2BDIPpIkSZIk/Z0ffoAOHSKvH3+Mfn3x4vDsszBjBpx+euDtScqKQglwbGfokALVbo18Hq1f\nP4fRdWH6HbBzY9AdSpIkSXET12H3J598st+pboBixYrx4osvUrx4sPcJFS1a9KB1d+7cySeffBLo\nXpIkSZIk7Wvbtsgp7ho1Iqe6Y3HllZCSErnf27u5pVwof0loMBDOmg5Hnhr9+vBuSHkGPk6CH9+G\n+N5sKEmSJAUirsPur7/+eu/Haae6u3btSvny5TNkv/Lly9O1a9cD4sz37UOSJEmSpCB9/HEksrx3\nb/jjj+jX164NkyfDm28aWS4JKFkXWk2OPdp8+2qYcgWMbwbr5wTdnSRJkpSp4jrsXrBgwX6fJyQk\ncMEFF2TonhdccAEJCX9+2eFw+IA+JEmSJElKryVLoH17OPvs2CPLBwyA6dPhtNOC709SNrY32nwR\nVLstxmjzSTC6HkzvDju84k+SJEnZU1yH3StWrNh7XzdAUlISZcrE8BupUShTpgzJycl7T5ID/Pzz\nzxm6pyRJkiQp99i2DR56KHKae+TI2GpcdRUsWgS33WZkuaS/kb8ENBgQiTYv0zj69eHdkPIsjEiC\nH98y2lySJEnZTlyH3Zs2bQL+jDAvV65cpuz7133S+pAkSZIkKVbhMAwfHrmX+5FHYossr1MHvvgC\n/vMfKFs28BYl5VQl60LLyXDym1DwqOjXb/8FpnSCT5vC77MDb0+SJEnKKHEddu/cuXO/z4sVK5Yp\n+xYtWnS/z3ft2pUp+0qSJEmScqa0yPJzzoGlS6Nff8QRMHAgTJsGjWM4nClJhEJw7JXQPgWqdY0t\n2nzNZBhzIkzvZrS5JEmSsoW4DrsLFSq03+e//PJLpuz766+/7vd5wYIFM2VfSZIkSVLOsnUr9OoV\niSwfNSq2Gp07Q0oK3HqrkeWSApC/BDR4Ds6aAWVOi359eDekPLcn2vx/RptLkiQpS4vrsLt06dIA\nhEIhwuEwP/74Y6bs++OPP+53V/iRRx6ZKftKkiRJknKGcBiGDYtElvfpE1tked268OWX8MYbRpZL\nygAl60DLSXDKf6FgDP8js/0XmHIlfNrEaHNJkiRlWXEddleuXJnwPr8d+ssvvzBt2rQM3XP69Oms\nXr0a+POu8MqVK2fonpIkSZKknGPxYmjXDs49F376Kfr1aZHl334Lp54aeHuS9KdQCI7pFIk2T7o9\nxmjzLyLR5tNuhx3rA29RkiRJSo+4Drvr1KlzwLPXXnstQ/c8WP3atWtn6J6SJEmSpOxv61Z48MFI\nZPno0bHVuPpqWLTIyHJJmSz/EVD/WTjru9ijzRcNiESb//Bfo80lSZKUZcR12N2kSZO9H6dFmY8Y\nMYKxY8dmyH7jxo1j+PDh+0WY/7UPSZIkSZL2FQ7D0KGRyPJHH4UdO6KvUbcufPUVvP46HHVU0B1K\n0mEqWTud0ea/wtSr4NPT4fdZwfcnSZIkRSmuw+6TTz6ZsvtcTJY28L7tttuYNGlSoHt9+eWX3Hbb\nbQcMuhMTEznV3DhJkiRJ0kF8/z20bQvnnRdbZHmJEjBoEEybBqecEnh7khS9/aLNu0EoT/Q11ny5\nJ9q8q9HmkiRJiqu4DrtDoRDXX3/9fvd2h0Ihtm7dytVXX82LL77Irl270rXH7t27eemll7jyyivZ\nsmXL3udp93Vfe+216aovSZIkScp5tm6Fnj2hVi0YMya2GtdcAykpcMstkCeGWZIkZaj8R0D9Z6DN\nd1Dm9OjXh1Nh0cA90eZvRj6XJEmSMlkoHI7vJTvbtm3jjDPO4Oeffwb+HEKn/Xnsscdyww030KFD\nB4oXL37YdTdt2sTHH3/MK6+8wuLFi/fW29fRRx/NhAkTKFiwYKBf01/Vr1+f1atXk5iYyPTp0zN0\nL0mSJElS7NIiy7t1g2XLYqtRr17kNLcnuSVlG+EwLP0/+O4u2L46thpHngoNB0HJuoG2JkmSJP2d\nuA+7IRIxftlll5Gauv9vgKa1FgqFyJ8/Pw0aNOCEE06gevXqHHnkkRQtWpTChQuzdetWNm/ezNq1\na5k/fz5z587l22+/ZceOHfvV2Ldu3rx5effddzn55JMz/Otz2C1JkiRJWd/338Ntt8HYsbGtL1EC\nHn8cbrjBk9ySsqmdG2H2w7BoAIR3R78+lABVb4HafSB/iYCbkyRJkg6UJYbdAP/5z3/o2bPnAaev\ngYMOrP/JX6PR//r8iSeeoFOnTrG2GxWH3ZIkSZKUdW3ZEhlSP/007NgRW41rr4UnnoAyZYLtTZLi\nYv0cmHYr/DoptvUFykC9vnDMlZEBuCRJkpRBssy/Njt37sxjjz1GnoP8+nsoFNobbX64r7Q1BzvR\n/eSTT2baoFuSJEmSlDWFw/Dhh1C9emTYHcug+8QTYcoUePVVB92ScpASJ0CLiXDq21AwMfr1f6yB\nqVfDJ6fBuu+C7k6SJEnaK8sMuwGuuuoq3nnnHSpUqMDBDpzvO8D+p9dfhcNhKlWqxPvvv88VV1yR\nGV+OJEmSJCmLWrQIzjoLLrgAli+Pfn3JkvDCC/DNN5AJt2NJUuYLhaDKZdAhBZLvgFAM9zP8NgXG\nNoBvb4UdvwffoyRJknK9LDXsBjjllFP47LPPuPPOOzniiCP2ntSORdraEiVK0KNHDyZMmECjRo0C\n7liSJEmSlF1s2QL33w+1asG4cbHVuO66yLD85pu9m1tSLpCvOJzYD9rMhKOaRr8+nArfD4KPk2DJ\nG5HPJUmSpIBkmTu7D2bbtm2MGjWKESNGMGXKFDZv3nzYa4sVK8app55K+/btOeussyhUqFAGdvr3\nvLNbkiRJkuIrLbK8e/fYTnID1K8PgwbBSScF25skZRvhMPz0Dnx3F2xbFVuN0idDw0FQ6sRge5Mk\nSVKulKWH3fvavXs3ixcvZuHChaxcuZI1a9awdetWdu7cSb58+ShcuDBlypShfPnyJCcnc/zxxx/0\n/u94cNgtSZIkSfGTkgK33QaffBLb+pIl4YknIie6s8i3mZIUXzs3wpzekPIchHdHvz6UAMffBHUe\nhfwlg+9PkiRJuUa2GXZnZw67JUmSJCnzbdkCjz4K/frBzp3Rrw+FIgPuxx+HI48Mvj9JyvbWz4Np\nt8KvE2NbX+BIqPsvOLZzZAAuSZIkRcl/RUqSJEmScpRwGD74AJKT4cknYxt0N2gAU6fCyy876Jak\nQypRE1pMgFPfgULlol//x2/w9bUw7lRYNyP4/iRJkpTj5Y13A5lt0KBBTJw4ce/noVCI999/P34N\nSZIkSZICs3BhJLL8009jW1+qVCSy/NprjSyXpMMSCkGVjlChHcx9BBY+C+Fd0dVY+zWMaQBVb4La\nj0KBUhnSqiRJknKeXDfsXrx4MVOmTCEUChEOhwmFQvFuSZIkSZKUTps3RyLL+/ePPbL8+usjkeWl\nSwffnyTlePmKQb2n4NirI9Hmv3wWZYEwfP8iLBsMdZ+M1DHaXJIkSf/AfzFKkiRJkrKtcBgGD4bq\n1eFf/4o9svzrr+Hf/3bQLUnpdkQNOGM8NH4XCpWPfv0fv8HX1+2JNp8efH+SJEnKURx2S5IkSZKy\npYULoVUruPhi+Pnn6NeXKhUZcE+dCg0bBt+fJOVaoRBUvgTaL4Tqd0MohnDJtV/DmIbwzc3wx7rg\ne5QkSVKO4LBbkiRJkpStbN4M99wDtWvD+PHRrw+F4MYbYdEiuOEG7+aWpAyTrxjU6wttZ0HZM2Io\nEIbFL8GIarD4VQinBt6iJEmSsjeH3ZIkSZKkbCEchvffh+Rk6Ns3tsjyhg3hm2/gpZeMLJekTHNE\nDTjj03REm6+Fb66HcafA2mnB9ydJkqRsy2G3JEmSJCnLW7AgEll+ySWwYkX060uXhldeiUSWN2gQ\nfH+SpH8QSLT5NzC2EXxzU2QALkmSpFzPYbckSZIkKcvatAl69EhfZPlNN0FKClx3HST4XbAkxdfe\naPPZULZFDAXCsPjfMCIJFr9itLkkSVIu57f5kiRJkqQsJxyG996LRJY/9RTs2hV9jUaNIpHlL75o\nZLkkZTlHVIczPoHT3odCFaJf/8da+OYGGHsyrP02+P4kSZKULTjsliRJkiRlKfPnQ8uW0LEjrFwZ\n/frSpeHVV2HKFCPLJSlLC4Wg0kWRaPMa98QWbb7uWxh7Enxzo9HmkiRJuZDDbkmSJElSlrBpE9x9\nN9SpAxMmRL8+FIKbb4ZFi+Daa40sl6RsI19RqPsktJ0DiS1jKBCGxS/Dx9Uif6buDrxFSZIkZU1+\n6y9JkiRJiqtwGN59NxJZ/vTTsUWWn3QSfPstvPAClCoVfI+SpExwRDI0HxeJNi9cMfr1O9ZFTniP\nM9pckiQpt3DYLUmSJEmKm3nzoEULuPTS2CLLjzwyEln+1VdQv37w/UmSMllatHm7BVDjXkjIF32N\nddMi0eZf3wDbfwu+R0mSJGUZDrslSZIkSZlu0ya46y6oWxc++yz69aEQ3HILpKQYWS5JOVK+olD3\niT3R5q1iKBCGJa/AiCT4/t9Gm0uSJOVQ/jhAkiRJkpRpwmF4551IZHm/frFFlp98MkybBoMGGVku\nSTle8SRoPhZOGxx7tPm3N8G4k+C3b4LvT5IkSXHlsFuSJEmSlCnmzYMzzoDLLos9svz11+HLL+HE\nE4PvT5KURYVCUOlCaL8wHdHm0yN3eX99vdHmkiRJOYjDbkmSJElShtq4Ee68E+rUgYkTo1+fkABd\nusCiRXD11UaWS1KulbfIPtHmZ8ZQIAxLXoUR1eD7l4w2lyRJygH8EYEkSZIkKUOEw/B//xeJLO/f\nH3bHMFM45ZRIZPnzz0PJksH3KEnKhoonQfMxcPoQKHx09Ot3/A7f3rwn2vzr4PuTJElSpnHYLUmS\nJEkK3Ny50Lw5XH45rFoV/foyZeCNN+CLL6BeveD7kyRlc6EQHH0+tF8ANe9PZ7T5dbB9TfA9SpIk\nKcM57JYkSZIkBWbjRrjjDqhbFz7/PPr1CQlw662QkgKdOxtZLkn6B3mLQJ3HoO3cGKPNgSWvwYgk\n+P5Fo80lSZKyGX9sIEmSJElKt3AY3n4bkpLgmWdiiyw/9VSYPh0GDjSyXJIUpeLV9ok2rxT9+h2/\nw7e3wNhG8NvU4PuTJElShnDYLUmSJElKlzlzoFkzuOIKWL06+vVpkeWTJ0dOhEuSFJP9os0fgIT8\n0df4fQaMOwWmXmu0uSRJUjaQN+iC/fv355lnngm6rCRJkiQpi9mwAR5+OHISO5aT3AkJ0KULPPII\nlCgRdHeSpFwrb2Go8ygccxVMvw1WjY2+xg+vw/IPIxHpx98ICXmC71OSJEnpliEnu8PhcJZ+SZIk\nSZJiFw7DW29BcjI8+2xsg+7GjSOR5QMGOOiWJGWQ4lWh2Wg4/cPYos13rodpXWBsQ1gzJfD2JEmS\nlH4ZFmMeCoWy7EuSJEmSFJs5c6BpU+jUKbbI8qOOgjffNLJckpRJQiE4+rx0Rpt/B5+cClOvge2/\nBt+jJEmSYpahd3bH+wS3J7slSZIkKRgbNkC3blCvXmRQHa2EBOjaFVJS4MorI7MHSZIyTVq0edu5\nUK5NbDV+eAM+ToJFgyA1hlgTSZIkBS5Dh93xPsHt6W5JkiRJSp9wGP73P0hKgueeiy2y/LTTYMaM\nyHojyyVJcVW8KjQbCU2GQpHK0a/fuR6m3QpjG8Car4LuTpIkSVHKsGF3vE9ve8JbkiRJktJn9mxo\n0iRyEvuXX6JfX7Ys/Pe/MGkS1KkTfH+SJMUkFIKK50C7+VDrwRijzWfCJ41h6tVGm0uSJMVRKOzU\nN8PVr1+f1atXk5iYyPTp0+PdjiRJkiT9rQ0boFcvGDQotpPcCQlw223QuzcccUTw/UmSFKhNi2Fa\nV1g1Orb1+Y6A2o9C1ZsgIW+wvUmSJOlvZWiMuSRJkiQp+wiHIyexk5JgwIDYI8u/+w6efdZBtyQp\nmyh2/D7R5lWiX79zA0y/DcY0gDVfBt2dJEmS/obDbkmSJEkSs2bB6afDVVelP7K8du3g+5MkKUPt\nF23eCxIKRF9j/Sz45DSY0hm2xfD/TCVJkhQ1h92SJEmSlIutXw9du8KJJ8KXMRxGy5MHunWDlBTo\n1CkyK5AkKdvKWwhq94Z286B829hq/PgmjEiClIGQuivY/iRJkrQfh92SJEmSlAulpsKbb0YiywcO\njHwerdNPj0SWP/OMkeWSpBym2HHQdAQ0GZaOaPOuMKY+/PpF4O1JkiQpwmG3JEmSJOUys2ZBkybQ\nuTP8+mv06xMT4a234PPP4YQTAm9PkqSsIRSCimenM9p8Nnx6Oky5ymhzSZKkDOCwW5IkSZJyifXr\n4bbb0hdZ3r17JLL88suNLJck5RL7RZu3j63Gj/+FEdUgZYDR5pIkSQFy2C1JkiRJOVxqKvznP1Ct\nGjz/fGyR5U2aRCLL+/eH4sUDb1GSpKyv2HHQ7GNoMhyKHBP9+p0bYfrte6LNJwffnyRJUi7ksFuS\nJEmScrDvvoPTToOrr4Y1a6JfnxZZPnGikeWSJAFQsUPklPcJD6cj2rwJfHUlbFsdeHuSJEm5icNu\nSZIkScqBfv8dbr0VGjSAKVOiX58nD9xxh5HlkiQdVN5CcMJD0H4+VOgQW42l/4MRSbDwOaPNJUmS\nYuSwW5IkSZJykNRUeOMNSEqCQYNiiyxv2hRmzoR+/YwslyTpbxU9FpoOh6YfRz6O1s6NMKMbjDnR\naHNJkqQYOOyWJEmSpBxixoxIZPk118QWWV6uHLz9Nnz2GdSqFXx/kiTlWBXa74k27w15Cka/fv2c\nPdHmnYw2lyRJioLDbkmSJEnK5n7/Hbp0gYYN0xdZvnAhXHaZkeWSJMUkT0E4oRe0mw8Vzo6txtK3\n9kSbP2u0uSRJ0mFw2C1JkiRJ2VRqKrz+OlSrBi+8EFtkebNmMGuWkeWSJAWm6DHQdBg0HZGOaPPu\nMLoe/Dop+P4kSZJyEIfdkiRJkpQNzZgBjRvDtdfCb79Fv75cOXjnHZgwAWrWDL4/SZJyvQrt0hdt\nvmEufNoUvroCtq0Kvj9JkqQcwGG3JEmSJGUj69bBLbdAgwYwdWr06/PmhbvugpQU6NjRyHJJkjLU\nvtHmFc+JrcbSt+HjJFj4DKTuDLY/SZKkbM5htyRJkiRlA6mp8NprkJQEL74I4XD0NZo3j0SWP/UU\nFCsWfI+SJOkQih4DTYZC05FQ9Ljo1+/aBDPugNEnwi+fB96eJElSduWwW5IkSZKyuOnT4dRT4brr\nYossL18+Elk+fjzUqBF8f5Ik6TBVaAvt5kLtPrFHm49vBl9eDltXBt6eJElSduOwW5IkSZKyqHXr\n4OaboWFD+Prr6NfnzQt33w0LFxpZLklSlpGnINTqCe0WQMVzY6vx0//BiCRY0N9oc0mSlKs57JYk\nSZKkLCY1FV59FapVg5deii2y/IwzIpHlffsaWS5JUpZUtAo0+QiajYKix0e/ftdm+O5OGF0PfpkY\ndHeSJEnZgsNuSZIkScpCpk2DU06B66+HtWujX1++PLz7Lnz6qZHlkiRlC+XbQLs5UPtRyFMo+vUb\n5sH45vDlZUabS5KkXMdhtyRJkiRlAWvXwk03QaNG8M030a/fN7L8kkuMLJckKVvJUxBqPQDtF0DF\n82Kr8dM7e6LN+xltLkmScg2H3ZIkSZIUR6mp8MorkJQE//53bJHlLVrA7NlGlkuSlO0VqQxNPoRm\no9MRbX4XjK4Lv3wWeHuSJElZjcNuSZIkSYqTtMjyG26ILbK8QgV4/3345BOoXj34/iRJUpyUPwva\nzU1HtPl8GH8GfHkpbF0RfH+SJElZhMNuSZIkScpka9fCjTemL7L8nnsikeUXXWRkuSRJOVKeAn9G\nmx99fmw1fnoXRiTDgqeNNpckSTmSw25JkiRJyiS7d8PLL0O1apE/Y4ksb9kS5syBJ5+EokWD71GS\nJGUxRSrD6UOg2RgoVjX69bs2w3d3G20uSZJyJIfdkiRJkpQJvv0WTj45cqJ73bro11esGIksHzcO\nkpOD70+SJGVx5VtD2zlQ5/H0RZt/0dFoc0mSlGM47JYkSZKkDPTbb5E7uU86KXJHd7Ty5YN774UF\nC4wslyQp18tTAGreB+0XwtEXxFZj2XswIgnmPwW7dwTbnyRJUiZz2C1JkiRJGWD3bvj3vyEpCV55\nJbbI8latIpHlTzxhZLkkSdpHkUpw+gfQfCwUqxb9+l1bYGYPGF0HVo8Pvj9JkqRM4rBbkiRJkgL2\nzTeRyPKbboo9snzwYBg7NjIslyRJOqhyZ0Lb2XuizQtHv37jQpjQEr64BLb+HHx/kiRJGcxhtyRJ\nkiQF5Lff4PrrI4Pu9ESWL1wIF15oZLkkSToMe6PNF8DRF8ZWY9n7MCIZ5vc12lySJGUrDrslSZIk\nKZ1274aXXoJq1eDVV2OLLD/zzD8jy4sUCb5HSZKUwxWpBKcPhubj0hFtfs+eaPNPg+9PkiQpAzjs\nliRJkqR0+PprOOkkuPlm+P336NcffTQMGQJjxhhZLkmSAlCu1Z5o8yfSEW3eCr642GhzSZKU5Tns\nliRJkqQY7BtZPn169Ovz5YP774cFC+D8840slyRJAcpTAGreC+0XQqWLYquxbPCeaPN/GW0uSZKy\nLIfdkiRJkhSF3bvhxRf/jCyPxZlnwty58NhjRpZLkqQMVORoOO19OOMTKB5DhMyuLTDzXhhd22hz\nSZKUJTnsliRJkqTDNHUqNGoEt9wSW2R5pUp/RpZXi+EqTUmSpJgktoQ2s6HuvyBvDL9ptzElEm0+\n+SLYsjz4/iRJkmLksFuSJEmS/sGaNXDttXDKKTBjRvTr8+eHBx4wslySJMVRnvxQo8eeaPOLY6ux\n/INItPm8J402lyRJWYLDbkmSJEk6hN274YUXIqewX389thqtW0ciyx99FAoXDrY/SZKkqBWuCKe9\ntyfaPDn69bu3wqz7YNQJsGpc8P1JkiRFwWG3JEmSJB3ElCmRyPIuXWD9+ujXV6oEH34Io0dD1aqB\ntydJkpQ+iS2hzazYo803LYLPWsPkC2HLsuD7kyRJOgwOuyVJkiRpH7/+CtdcA6eemv7I8vPOM7Jc\nkiRlYftFm18SW43lQ2BEdZj3BOz+I9j+JEmS/oHDbkmSJEkiElk+aBAkJcEbb8RWo00bI8slSVI2\nVLginPYunPEpFK8e/frdW2HW/ZFo85Vjg+9PkiTpEBx2S5IkScr1pkyBhg3h1ltjiyyvXBmGDoWR\nI40slyRJ2VhiC2gzE+r2jTHa/HuYeBZMvsBoc0mSlCkcdkuSJEnKtfaNLP/uu+jX588PDz4I8+fD\nOecYWS5JknKAPPmhxt3pjDb/EEYkw7zHjTaXJEkZymG3JEmSpFxn1y54/vn0R5bPmwePPGJkuSRJ\nyoH2RpuPjzHafBvMesBoc0mSlKEcdkuSJEnKVb78Eho0gNtuiy2yvEqVPyPLjz8+4OYkSZKymsQz\noO0sqPc05C0a/fq0aPNJ58OWn4LvT5Ik5WoOuyVJkiTlCr/8Ap07w2mnwaxZ0a8vUAB69TKyXJIk\n5UIJ+aD6nZFo88qXxlbj549gRHWY+5jR5pIkKTAOuyVJkiTlaLt2wcCBkcjyN9+MrUbbtpHI8t69\noVChYPuTJEnKNgpXgMb/By0mwBE1ol+/exvM7gkja8HKMcH3J0mSch2H3ZIkSZJyrLTI8q5dYcOG\n6NdXqQLDhsGIEXDccYG3J0mSlD2VbQ5tZsYebb55MUxsA5POg81Lg+5OkiTlIg67JUmSJOU4v/wC\nV10VTGT52WcbWS5JknSAvdHmKVD5sthq/DwURtaAuY/C7u2BtidJknIHh92SJEmScoxdu2DAAKhW\nDf7739hqtG9vZLkkSdJhK1weGr8NLT6DI2pGv373Npj9IIw8AVaODr4/SZKUoznsliRJkpQjfPEF\n1K8Pt98OGzdGv/6YY2D4cPj4YyPLJUmSola2GbT5Dur1g7zFol+/eTFMbAuTzjXaXJIkHTaH3ZIk\nSZKytbTI8tNPh9mzo19foAA8/HDkNHeHDoG3J0mSlHsk5IPqd0D7hemINh8GI6vDnD5Gm0uSpH/k\nsFuSJElStrRrFzz3XPoiyzt0iNzL/dBDRpZLkiQFZm+0+UQ4olb063dvhzm9YGQtWDEq6O4kSVIO\n4rBbkiRJUrYzeTKceCJ06xZ7ZPnHH0diy489NvD2JEmSBFC2KbSZASc+E2O0+RL4vB18fg5s/jH4\n/iRJUrbnsFuSJElStrF6NXTqBE2awJw50a8vWPDPyPL27QNvT5IkSX+VkA+Su0GHFKhyRWw1VgyH\nkTVgziNGm0uSpP047JYkSZKU5e3aBc8+C0lJ8NZbsdU4+2wjyyVJkuKmUDk49X/Q8vN0RJs/BCNr\nwoqRwfcnSZKyJYfdkiRJkrK0SZMikeXdu8cWWX7ssTBiBAwbFokvlyRJUhwd1eTPaPN8xaNfv/kH\n+Lw9fH620eaSJMlhtyRJkqSsadUquOIKaNo09sjy3r0jkeXt2gXfnyRJkmKUFm3ePgWqdIqtxoqP\n90Sb94Zd2wJtT5IkZR8OuyVJkiRlKTt3wjPPRCLL3347thrnnBOJLO/VKzL0liRJUhZUKBFO/S+0\nnAQlToh+/e7tMOdhGFULVowIvD1JkpT1OeyWJEmSlGWkRZbfcQds2hT9+uOOg5EjYehQI8slSZKy\njaNOh7NmwInPpiPavANM7BD5WJIk5RoOuyVJkiTF3b6R5XPnRr++YEHo0yeytm3b4PuTJElSBkvI\nC8m3py/afOUIGFEDZj9stLkkSbmEw25JkiRJcbNzJ/Tvn77I8nPPhQULoGdPI8slSZKyvb3R5pOh\nRO3o16f+AXN7w8ia8PPHwfcnSZKyFIfdkiRJkuJi4kSoVw/uvDP2yPJRo+Cjj6BKlaC7kyRJUlwd\ndRqcNR3qD4gt2nzLjzDpbJjYHjYtCb4/SZKUJTjsliRJkpSpVq6Eyy6D5s1h3rzo1xcq9GdkeZs2\nwfcnSZKkLCIhLyTdBu0XwTFXxVZj5cjIKe/ZDxltLklSDuSwW5IkSVKm2LkT+vWLRJa/805sNc47\nz8hySZKkXKdQWTjlP9DqCyhRJ/r1qX/A3EdgZA34eTiEw4G3KEmS4sNhtyRJkqQMN3Ei1K0Ld90F\nmzdHv/7442H0aPjwQ6hcOejuJEmSlC2UaQxnTdsTbX5E9Ou3LIVJ58DnRptLkpRTOOyWJEmSlGFW\nrIBLL41Els+fH/36QoXg0UcjkeVnnRV8f5IkScpm9kabp6Qj2nzUnmjzXrBra7D9SZKkTOWwW5Ik\nSVLgdu6Ep5+G5GR4993Yapx/fiSy/IEHoECBYPuTJElSNrc32vxLKFk3+vWpf8DcPpGh98/DjDaX\nJCmbctgtSZIkKVCffRaJLL/77tgiy6tWhTFjYMgQI8slSZL0D8qcCq2/hfoD0xFtfi5MbAebFgfd\nnSRJymAOuyVJkiQFIi2y/IwzYo8sf/xxmDMHWrcOvj9JkiTlUAl5IelW6LAIju0cW41VoyOnvGc9\naLS5JEnZiMNuSZIkSekSRGT5BRfAwoVw331GlkuSJClGBY+Ck99IR7T5Dpj3KIysAcuHGm0uSVI2\n4LBbkiRJUswmTIA6dWKPLK9WDcaOhQ8+gEqVgu9PkiRJuVCZU6H1NGgwCPKViH79lp9g8nlGm0uS\nlA047JYkSZIUtZ9/hksugRYtYMGC6NcXLhyJLJ89G848M/j+JEmSlMsl5IFqt0CHFDj2mthq7I02\n72m0uSRJWZTDbkmSJEmHbccO6Ns3Eln+/vux1bjwwsiA3MhySZIkZbiCR8HJr0Grr6BkvejXp+6A\neY/BiOqw/COjzSVJymIcdkuSJEk6LOPHRyLL77kHtmyJfn21ajBuHAwebGS5JEmSMlmZU6D1t7FH\nm29dBpPPh4ltYOP3gbcnSZJi47BbkiRJ0t/6+We4+GJo2RIWLox+feHC8MQTkcjyVq2C70+SJEk6\nLHujzRf9P3v3HSZldbcB+Fk6otgVe4kCKlixYO+igL33ErtJ7CWWGGM0GnuvsWuiidGIYu+KIPYG\nqLH3hqAgdb8/Bo1+LMq8Oyw7u/d9XbmQM3vO/AyLMTxznrce1eb3JHd1S144Nhlf4BOgAEBFCbsB\nAIA6jR2bnHZaqbL8lluKnbH11qWA/OijVZYDANBItJuzVG2+4YBk1uXL3z9xbPLKKUm/JZP3blVt\nDgDTkbAbAACYzP33J0svXQqpi1SWd+nyv8ryBRao/HwAAFBvc6ySbDQoWfGipM2s5e8f9W7y2FbJ\nQ72SEcMqPx8A8IuE3QAAwA/ee69UWb7BBsnQoeXv79ChdBtcZTkAAFWhRctk8f2TPkOTX+1V7IyP\n7y1Vmz//e9XmANDAhN0AAEBFKsu33bZUWX7kkUmbNpWdDwAApql2cyYrX1GPavNxyaunJv2WSN79\nl2pzAGggwm4AAGjm7rvvf5Xlo0aVv79r19IZ//hHMv/8lZ8PAAAazA/V5hcXrDZ/L3l8a9XmANBA\nhN0AANBMvftusvXWyYYb1q+y/IUXkvXXr/x8AAAwXbRomSy+X9JnWPKrvZPUlH/GD9Xmx6g2B4Bp\nSNgNAADNzJgxyamnJksskfzrX8XO2G47leUAADRx7eZIVr4s2fCpZLYe5e+fOC559S9Jv67Ju/9U\nbQ4A04CwGwAAmpF77y1Vlv/+98Uqy5dYIrn//uTvf1dZDgBAMzHHSqXAe8VLkjazlb9/1PvJ49sk\nD22YfD2k8vMBQDMm7AYAgGbg3XeTrbZKNtooGVbg0YEdOiSnn548/3yy3noVHw8AABq3Fi2TxfdN\n+gytR7X5/Un/pZPnj07GfVPxEQGgORJ2AwBAEzZmTHLKKUnXrsmttxY74/vK8iOOUFkOAEAz9321\n+UYD61Ftflpy5xLJu7eoNgeAehJ2AwBAE3XPPUn37smxxyajR5e/f4klkgceUFkOAACTmX3FUrX5\nSpfWo9p82+TBDVSbA0A9CLsBAKCJ+b6yvFev5PXXy98/44zJGWckL7yQrLtu5ecDAIAmoUXLZLF9\nkr7DSj8WqTb/5IFStflzR6k2B4AChN0AANBEVKKyfIcdSpXlhx2WtG5d2fkAAKBJajt76Yb3RgOT\n2VYsf//Ecclrpyf9uibv3KzaHADKIOwGAIAm4O6761dZvuSSyYMPJjfemMw3X+XnAwCAJm/2FZON\nnkpWuqwUgJdr9AfJE9tNqjZ/rfLzAUATJOwGAIAq9vbbyRZbJBtvXL/K8uefT9ZZp9LTAQBAM1PT\nIlls76TP0GSx/VK42vyupZPnjkzGjaz4iADQlAi7AQCgCn33XXLyyaUb2bfdVuyMHXdMhg5VWQ4A\nABXXdvZkpYuTjQYls69U/v7a8clrf51Ubf4P1eYAMAXCbgAAqDL9+5cqy48/vlhl+VJLJQ89lNxw\nQzLvvJWfDwAAmGT2HsmGA5KVLi9Ybf5h8sT2yYPrJ1+/Wvn5AKDKCbsBAKBKfF9ZvskmyRtvlL9/\nppmSM89MnnsuWXvtSk8HAADUqaZFstivkz7D6lFt/mBy1zLJc0eoNgeAHxF2AwBAI/fdd8mf/pQs\nsUT9KsuHDEkOPVRlOQAATBdtZytVm/d6Opl95fL3145PXjujVG3+9t9VmwNAhN0AANCo3XVX0q1b\ncsIJpdC7XN26JQ8/rLIcAAAajdlWSDZ8Mln5iqTtHOXvH/1h8uQOyYPrJcNfqfx8AFBFhN0AANAI\nvf12svnmSe/eyZtvlr9/ppmSs89Onn02WWutSk8HAADUS02L5Fd7JX2GJovvn2LV5g8l/ZdNnj1c\ntTkAzZawGwAAGpEfV5bffnuxM3beORk6NDn4YJXlAADQqLWdLVnxovpVmw85c1K1+U2qzQFodoTd\nAADQSNx5Z/0ryx95JLnuumSeeSo/HwAAMI38UG1+ZT2qzXdMHlhXtTkAzYqwGwAAprO33ko23TTp\n06f+leVrrln5+QAAgAZQ0yL51Z5J32HJ4geWfl6uTx+eVG1+WDJuRKUnBIBGR9gNAADTyejRyR//\nmCy5ZHLHHcXOUFkOAABNTJtZkxUvSDYanMzRs/z9teOTIWdNqja/UbU5AE2asBsAAKaDfv1KteMn\nnlissrx79+TRR1WWAwBAkzXbcskGjycr/y1pO2f5+0d/lDy5U/LAOsnwlys/HwA0AsJuAABoQP/9\nb6myvG/f0l+Xq2PH5JxzSpXla6xR8fEAAIDGpKZF8qs9kr5D61Ft/kip2vyZQ1WbA9DkCLsBAKAB\njB5dusVdn8ryXXYpVZb/7ndJq1YVHQ8AAGjM6l1tPiEZenZyR5fkrRtUmwPQZAi7AQBgGrvjjmSp\npUrP5x4zpvz9Sy+dPPZYcu21SadOlZ8PAACoEt9Xm69yVbFq8+8+TgbsnDywdjL8pYqPBwANTdgN\nAADTyH//W6or33TT5K23yt/fsWNy3nnJM88kq69e+fkAAIAqVNMiWXT3pO+wpPNBBavNH036L5c8\nc0gy9uuKjwgADUXYDQAAFfbjyvJ+/YqdsdtuybBhyW9+o7IcAACoQ5tZkh7nJ72eSeZYtfz9tROS\noeck/bomb12v2hyAqiTsBgCACqpvZfkyyySPP55cfXUy99wVHw8AAGhqZl022eCxZJWrk3Zzlb//\nu4+TAbsk96+l2hyAqiPsBgCACnjzzaRPn+KV5TPPXKosHzw4WW21ys8HAAA0YTUtkkV3S/oMTTr/\ntli1+WePTao2P1i1OQBVQ9gNAAD1MGpUcsIJpdvcd95Z7IzddkuGDlVZDgAA1FObWZIe5ya9nk3m\nLPAp2toJydBzk35dkreuU20OQKMn7AYAgAJqa5Pbby+F3H/6U7HK8mWXTZ54QmU5AABQYbMuk6z/\nWLLKNQWrzT9JBuya3L9m8tWLlZ8PACpE2A0AAGV6441SZfnmmydvv13+/plnTs4/P3n66WTVVSs9\nHQAAQJKammTRXetZbf54cvfyyeDfqTYHoFESdgMAwFQaNSo5/vjSbe677ip2xu67J8OGJQcdpLIc\nAABoAD+pNl+9/P21E5Jh55Wqzf97rWpzABoVYTcAAPyC2trkttuSJZdMTj45GTu2/DO+ryy/6qpk\nrgItggAAAPUy6zLJ+o8mPa9N2hV4jtJ3nyRP7Zbcv0by1QuVnw8AChB2AwDAz3jjjaR372SLLZJ3\n3il//yyzJBdemAwerLIcAACYzmpqkkV2KVWbd/ldUtOy/DM+e2JStflvk7HDKz4iAJRD2A0AAHX4\ncWV5//7Fzthzz2To0OSAA5KWBf4MCQAAYJpoM3Oywjn1qDafmAw7f1K1+TWlnwPAdCDsBgCAH6lE\nZflyyyVPPplceaXKcgAAoBGbdelJ1ebXFaw2/zR5avfk/jVVmwMwXQi7AQBgktdfTzbZpP6V5U8/\nnfTsWfHxAAAAKq+mJllk50nV5gerNgegqgi7AQBo9r79Njn22KRbt+Tuu4udseeeybBhKssBAIAq\n1WbmZIWzk42fS+Zas/z9P6k2v1q1OQANQtgNAECzVVub3HprqbL8lFOKVZYvv3wyYECpsnzOOSs/\nIwAAQIOapXuy3sNJz+uTdp3K3//dp8lTeyT3rZ58+VylpwOAnxB2AwDQLA0blmy8cbLVVsm775a/\nf9ZZk4suSgYNSlZZpfLzAQAATDc1NckiOyV9hyZdDilWbf75gOSeHsnTByVjv6r8jAAQYTcAAM3M\nt98mv/990r17cs89xc7Ya69k6NBk//1VlgMAAE1Y647JCmclGz9fvNr89QuTO7okb16l2hyAihN2\nAwDQLNTWJv/6V7LEEsmpp9avsvyKK1SWAwAAzcgs3UrV5qvekLSfp/z9Yz5LBu45qdr82UpPB0Az\nJuwGAKDJGzYs6dUr2Xrr5L33yt8/66zJxRerLAcAAJqxmppk4R2TPkOSrofWo9p8xeTpA1WbA1AR\nwm4AAJqs7yvLu3VL7r23/P01Ncnee5fC8v32U1kOAACQ1h2T5c+cVG2+Vvn7aycmr1+U3NE5efNv\nqs0BqBdhNwAATc7/rywfN678M3r0SJ56KrnssmSOOSo/IwAAQFWbpVuy3kPJqjcWrDb/PBm4V3Lv\naqrNAShM2A0AQJMydGiy0UbFK8tnmy255JJS0L3SSpWfDwAAoMmoqUkW3mFStflhSU2r8s/44qnk\n7h6qzQEoRNgNAECT8M03ydFHJ927J/fdV/7+7yvLhw5N9t1XZTkAAMBUa90xWf6MZJMXkrnXKXBA\n7Y+qza9UbQ7AVBN2AwBQ1Wprk1tuKVWWn3Za8crygQNVlgMAANTLzEsm6z6QrHpT0n7e8veP+TwZ\n+Ovk3lWTL5+p/HwANDnCbgAAqtaQIcmGGybbbpu8/375+2ebLbn00lJl+YorVn4+AACAZqemJll4\n+1K1+RKHF6w2H5jcvWIyaP9kzJeVnxGAJkPYDQBA1fm+snzppZP77y9/f01Nss8+ybBhpR9VlgMA\nAFRY65mS5f5av2rzNy5J+nVO3rhCtTkAdRJ2AwBQNWprk5tvrl9l+YorlirLL700mX32ys8IAADA\nj3xfbb7a3wtWm3+RDNo7ubdn8sXgys8HQFUTdgMAUBVeey3ZYINku+2KVZbPPnvpmdwqywEAABpY\nTU2y0HaTqs2PKFhtPii5Z6Vk0H6lABwAIuwGAKCR++ab5KijSpXlDzxQ/v6ammS//ZKhQ5O9905a\n+DdgAACA6aP1TMlypyebvJjMvW6BA2qTNy5N+nVJ3rhctTkAwm4AABqn7yvLu3ZNTj89GT++/DNW\nWikZNCi5+GKV5QAAAI3GzEsk696frPaPpP185e8f80UyaB/V5gAIuwEAaHxeey1Zf/1SZfkHH5S/\nf/bZk8svTwYMSHr0qPx8AAAA1FNNTbLQtpOqzY9UbQ5AIcJuAAAajZEjkyOOKFWWP/hg+fu/rywf\nNiz59a9VlgMAADR6rWdMljst2eSlpNP6BQ6YVG1+R+fkjcuSiRMqPiIAjZc//gMAYLqrrU3+/vdS\nZfkZZxSrLF955eTpp0uV5bPNVvkZAQAAmIZm7pqsc2+y+s3JDPOXv3/sl8mgfZN7V0m+eLry8wHQ\nKAm7AQCYrl59NVlvvWSHHZIPPyx//xxzJFdckTz5ZLLCCpWfDwAAgAZSU5MsuE3S+7VkyaOSFq3L\nP+PLwck9KycD90m++7zyMwLQqAi7AQCYLr6vLF9mmeShh8rfX1OT7L9/MnRostdeKssBAACajNYz\nJsv+Jdn4xeLV5m9envTrkrx+qWpzgCbMHwkCANCgamuTm26qTGX5RRepLAcAAGiyfqg2v6V4tfnT\n+5WqzT8fVPn5AJjuhN0AADSYV15J1l032XHH4pXlV16pshwAAKDZqKlJFtw66TMkWfLo4tXm966S\nDNxbtTlAEyPsBgBgmhs5Mjn88GTZZZOHHy5/f4sWyYEHJsOGJXvuqbIcAACg2WnVIVn21GSTl5JO\nGxQ4oDZ584qkX+fk9UtUmwM0Ef6YEACAaeb7yvIuXZIzzyxWWd6zZzJ4cHLBBcmss1Z+RgAAAKpI\nxy7JOvckq/8zmWGB8veP/Sp5ev/k3pWTzwdWfj4AGpSwGwCAaeKVV5J11ilVln/0Ufn755wz+dvf\nkscfT5ZbrvLzAQAAUKVqapIFt0r6vJYseUzBavNnVJsDNAHCbgAAKmrEiOSww5JllkkeeaT8/d9X\nlg8dmuyxh8pyAAAApqBVh2TZU5JNXk46bVjsjB+qzS9WbQ5QhfzRIQAAFVFbm9xwQ6my/KyzkgkF\n/oxAZTkAAABl69g5WefuZI1/JTMsWP7+sV8lTx+Q3LNS8vlTlZ8PgGlG2A0AQL29/HKy9trJzjsn\nH39c/v4550yuukplOQAAAAXV1CQLbJn0eTVZ6vdJizbln/HVs8m9PZOn9kq++6zyMwJQccJuAAAK\nGzEiOfTQZNllk0cfLX9/ixbJQQclw4Ylu++ushwAAIB6atUhWebPySYvJfNsVOyM//4tuaNzMuwi\n1eYAjZw/TgQAoGy1tcn115cqy88+u1hl+aqrJs88k5x/fjLLLBUfEQAAgOasY+dk7f7JGrcWqzYf\nNzwZfKBqc4BGTtgNAEBZXnopWWutZJddilWWzzVXcvXVyWOPlW6EAwAAwDRRU5MssEXS57VkqWPr\nWW2+Z/Ldp5WfEYB6EXYDADBVvv46OeSQ0jO1H3us/P0tWiS//W0ydGiy224qywEAAGggrWZIljk5\n2eTlZJ5exc7471XJHV2SYReqNgdoRPwRIwAAP+vHleXnnFOssny11ZJnn03OPVdlOQAAANNJx8WT\nte9K1vh3ParND0ruWTH5bEDFxwOgfMJuAACm6MUX/1dZ/skn5e+fa67kmmtKN8GXWaby8wEAAEBZ\namqSBTafVG1+XMFq8+eS+1ZVbQ7QCAi7AQCYzNdfJwcfnCy/fP0ry3fdtfRnCQAAANBotJohWeZP\nSe9Xknk2LnbG99XmQy9IJo6v7HwATBVhNwAAP6itTa69tlRZfu65xSrLV19dZTkAAABVYqbFkrXv\nTNa8LemwUPn7xw1PnvlNcneP5LMnKj0dAL9A2A0AQJLkhReSNddMdtutWGX53HOXgvJHH1VZDgAA\nQBWpqUnm3yzp/WrS7fikRdvyzxj+QnLf6smA3ZPRBf5PNQCFCLsBAJq54cOT3/2uVFn++OPl72/Z\nsrR/6NDSs71VlgMAAFCVWs2QLH1S0vvlZN5Nip3x1jVJvy7J0PNVmwM0AGE3AEAzNXFics01pcry\n884r/bxc31eWn3NOMvPMFR8RAAAAGt5MiyVr9UvWvD3psHD5+8d9nTzzW9XmAA1A2A0A0Ax9X1m+\n++7Jp5+Wv79Tp+S660qV5UsvXfHxAAAAYPqqqUnm33RStfkJ9aw23021OcA0IuwGAGhGhg9Pfvvb\nUmX5EwU+XN6yZXLIIaXK8p13VlkOAABAE9eqfbL0H5PeryTz9i52xlvXJv06J0PPU20OUGHCbgCA\nZuDHleXnn1+ssnzNNZPnnkvOOivp2LHyMwIAAECjNdOvkrX7JWv+p2C1+Yjkmd8ld6+QfPp4xccD\naK6E3QAATdzzzydrrFG/yvLrr08efjjp3r3CwwEAAEA1mb/vpGrzPxSsNn8xuX8N1eYAFSLsBgBo\nooYPT37zm2SFFZInnyx//48ry3faSWU5AAAAJJlUbX7ipGrzPsXOUG0OUBHCbgCAJmbixOSqq5LO\nnZMLLiheWf788yrLAQAAYIpm+lWy9h3JWnckHRYpf/9Pqs0fq/x8AM2AsBsAoAl57rlk9dWTPfdM\nPvus/P3zzJPccEOpsrxbt4qPBwAAAE3PfH1Kt7y7n5i0bFf+/uEvJvevmTy5SzL644qPB9CUCbsB\nAJqAr75KDjoo6dEjGTCg/P0tWyaHHpoMGZLsuKPKcgAAAChLq/ZJ9z+UQu/5+hY74+3rk35dkiHn\nqDYHmErCbgCAKvZ9ZXmXLsmFFxarLF9rrVJl+ZlnqiwHAACAeplx0WSt/yRr9Sv9dbnGjUiePSS5\ne/nk00crPx9AEyPsBgCoUs8+m6y2Wv0qy2+8MXnoIZXlAAAAUFHz9Z5Ubf7HgtXmLyX3r5U8uXMy\n+qPKzwfQRAi7AQCqzFdfJQceWKosf+qp8ve3apUcdlipsnyHHVSWAwAAwDTRsl3S/YSk96vJfJsW\nO+PtG5I7uiRDzk4mjqvsfABNgLAbAKBKTJyY/O1vSefOyUUXJbW15Z+xzjrJCy8kZ5yhshwAAAAa\nxIyLJGvdXrzafPzI5NlDk/6qzQH+P2E3AEAVePbZZNVVk732Sj7/vPz9886b3HRT8sADyZJLVn4+\nAAAA4Bf8UG1+UrFq869fVm0O8P8IuwEAGrEvv0wOOKBUWT5wYPn7W7VKDj+8VFm+/fYqywEAAGC6\natku6X58qdp8/s2KnaHaHOAHwm4AgEZo4sTkiitKleUXX1y/yvK//jWZaabKzwgAAAAUNOMiyZq3\nJWvflcz4q/L3/1BtvlzyySMVHw+gWgi7AQAamWeeKVWW77138sUX5e+fd97k739XWQ4AAACN3rwb\nJ71fTpb+U9Kyffn7v34leWDt5Ikdk1EfVnw8gMZO2A0A0Eh8+WWy//7JiisWryw/4ohSZfl226ks\nBwAAgKrQsl3S7bhJ1eabFzvjnZuSfl2S185UbQ40K8JuAIDp7MeV5ZdcUqyyfN11kxdfTE4/XWU5\nAAAAVKUZF07W/PekavPFyt8//pvkucOT/ssmnzxc4eEAGidhNwDAdDR4cNKzZ/HK8vnmS/7xj+T+\n+5Mllqj8fAAAAEADm3fjpPdLydInF6w2fzV5YJ3kiR2SUR9Ufj6ARkTYDQAwHXzxRbLffslKKyWD\nBpW/v1Wr5MgjS5Xl226rshwAAACalJbtkm7HJn1eS+bfotgZ7/w96dc1ee0M1eZAkyXsBgBoQBMn\nJpdfXqosv/TSYpXl66+fvPRSctppyYwzVn5GAAAAoJHosFCy5q3J2v3rUW1+xKRq84cqPh7A9Cbs\nBgBoIE8/nayySrLPPsmXX5a/f/75k5tvTu69N+natfLzAQAAAI3UvL2S3i8ny/y5HtXm66o2B5oc\nYTcAwDT2xRfJvvsmK69cCrzL1bp1ctRRyWuvJdtso7IcAAAAmqWWbZOlfl+qNl9gy2JnqDYHmhhh\nNwDANDJhQqmqvHPn5LLLileWv/hi8pe/qCwHAAAAUqo2X+NfyTr3JDN1Ln//99Xmdy2TfPxg5ecD\naEDCbgCAaWDQoFJl+X77Fa8sv+UWleUAAADAFMyzYbLJi8kypyQtZyh//4jXkgfXSx7fLhn1fuXn\nA2gAwm4AgAr6/PPSM7lXWSUZPLj8/a1bJ0cfnQwZkmy9tcpyAAAA4Ge0bJssdcykavOtip3x7s2l\navNXT08mjK3sfADTmLAbAKACvq8s79IlufzyYpXlG2yQvPRScuqpSYcOlZ8RAAAAaKI6LJis8c96\nVJt/mzx/VNJ/meTjByo/H8A0IuwGAKingQOTlVcuXlm+wALJP/+Z3HNPKSwHAAAAKOSHavNTC1ab\nD0keXF+1OVA1hN0AAAV9/nmy996lyvJnnil/f+vWyTHHJK+9lmy1lcpyAAAAoAJatk2WOjrpMyRZ\nYOtiZ/xQbX6aanOgURN2AwCUacKE5JJLks6dkyuuKHbGhhsmL7+cnHKKynIAAABgGuiwQLLGLck6\n9yYdC1TJjf82ef7opP/Sycf3V34+gAoQdgMAlGHgwGSllZL990+++qr8/QsumPzrX8ndd5fCcgAA\nAIBpap4Nko1fTJb9S8Fq86HJgxskj2+bfPte5ecDqAdhNwDAVPjss+TXvy5Vlj/7bPn727RJfv/7\n5NVXky23VFkOAAAANKCWbZIljypVmy+4TbEz3r1FtTnQ6Ai7AQB+xoQJyUUXJV26JFdeWeyMjTZK\nXnop+fOfVZYDAAAA01GHBZLVb07WvS/p2LX8/RNG/a/a/KP7Kj8fQJmE3QAAU/DUU6XK8gMPLF5Z\nfuutSf/+KssBAACARqTT+snGLyTLnpa0KvDJ/BFDk4c2TB7bOvn23crPBzCVhN0AAP/PZ58le+2V\n9OxZvLL82GOT115LtthCZTkAAADQCLVskyx55KRq822LnfHev5J+SySvnJpMGFPZ+QCmgrAbAGCS\n7yvLO3dO/va3Ymf06pW8/HJy8snJDDNUdj4AAACAipth/mT1fyTr3l+82vyF3yd3LZ18dG/l5wP4\nGcJuAIAkAwYkK65YqiwfPrz8/QsumPz738lddyWLL17x8QAAAACmrU7rTao2P71YtfnIYclDG6k2\nBxqUsBsAaNY+/TTZc89k1VWT554rf3+bNslxx5UqyzffXGU5AAAAUMVatkmWPGJStfl2xc74odr8\nFNXmwDQn7AYAmqUJE5ILL0y6dEmuuqrYGRtvnLzySvKnP6ksBwAAAJqQGeZPVv97su4DScclyt8/\nYVTywrHJXd2TD++p/HwAkwi7AYBm58knkx49koMOKlZZvtBCyW23JXfemSy2WKWnAwAAAGgkOq2b\nbPx8stxfC1abv5483Ct5bCvV5sA0IewGAJqNTz9N9tgjWW215Pnny9/ftm1y/PHJq68mm22mshwA\nAABoBlq2SZY4POkzNFlo+2JnvHdr0q+ranOg4oTdAECTN358cv75SefOydVXFztjk02Sl19OTjpJ\nZTkAAADQDM0wX7LaTcl6DyYzL1n+/gmjf1Rtfnfl5wOaJWE3ANCkPfFEqbL8t79Nvv66/P0LL5zc\nfnvSr5/KcgAAAIDMvc6kavMzklYzlr9/5OvJwxsnj26RfPN2pacDmhlhNwDQJH3ySbL77snqqycv\nvFD+/rZtkxNOKFWWb7qpynIAAACAH7RonSxx2KRq8x2KnfH+bcmdSyYvn5xM+K6i4wHNh7AbAGhS\nvq8s79IlueaaYmf07p288kryxz8m7dtXdj4AAACAJmOGeZPVbkzWe6h4tfmLxyd3dk8+7F/5+YAm\nT9gNADQZjz+erLBC/SrL//OfUmX5r35V8fEAAAAAmqa5155UbX5m0mqm8vd/80by8CaqzYGyCbsB\ngKr3ySfJbrsla6yRvPhi+fvbtk3+8IdSZXnfvpWfDwAAAKDJa9E6WeLQpM+QZKEdi53x/m3JnUsk\nL/1JtTkwVYTdAEDVGj8+Oe+8pHPn5Npri53Rt28p5D7xRJXlAAAAAPU2w7zJajck6z2czLxU+fsn\nfJe8dEJyZ7fkg7sqPR3QxAi7AYCq9Nhjpcry3/0uGTGi/P2LLJLccUeptnzRRSs/HwAAAECzNvda\nycbPJcufVbDa/M3kkd7Jo5urNgemSNgNAFSVjz9Odt01WXPNYpXl7dqVbnG/8krSp0/FxwMAAADg\ney1aJ10PSfoOTRbeqdgZ79+u2hyYImE3AFAVxo9Pzjkn6dIlue66Ymf07VsKuf/wB5XlAAAAAA2m\n/TzJqtdPqjbvVv7+n1Sb31np6YAqJuwGABq9Rx9Nll8+OeSQYpXliy6a9OunshwAAABgupp7rWTj\nZ5Plz65HtXmf5JHNkm/eqvx8QNURdgMAjdZHHyW77JKstVby0kvl72/XLvnjH0u3uXv3rvx8AAAA\nAJSpReuk68GTqs13LnbGB/9J7lwyeemPyfjRFR0PqC7CbgCg0flxZfn11xc7Y9NNk1dfTU44oRR6\nAwAAANCItJ8nWfW6ZP1Hklm6l79/wnfJSycmd3VLPuhX8fGA6iDsBgAalUcfTZZbrlRZPnJk+fu/\nryy//fZkkUUqPx8AAAAAFTTXmkmvZ5Plz0ladyx//zf/TR7pmzyyaemvgWZF2A0ANAoffZTsvHOp\nsvzll8vf365dctJJKssBAAAAqk6LVknX3yV9hiYL71LsjA/uSPotmbx4ompzaEaE3QDAdDVuXHL2\n2aXK8htuKHbGZpuVKsuPP15lOQAAAEDVat8pWfXaZP1Hi1WbTxyTvPzH5M6lkvfvqPx8QKMj7AYA\npptHHilVlh96aLHK8l/9KrnrruS221SWAwAAADQZc61RqjZf4dxi1ebfvpU8umnycF/V5tDECbsB\ngAb34YfJTjsla69dqh0vV/v2yZ/+VKo733jjio8HAAAAwPTWolXS5belavNFdi12xof9VJtDEyfs\nBgAazLhxyZlnlirLb7yx2Bmbb16qLD/uOJXlAAAAAE1e+05Jz2uS9R9LZlm6/P2qzaFJE3YDAA3i\n4YeTZZdNDj88+eab8vcvtljSv3/y738nCy9c4eEAAAAAaNzmWj3p9UyywnlJ65nL3/9DtXmfZOSb\nlZ8PmC6E3QDANPXhh8mOOybrrFO6kV2u9u2Tk08uVZb36lX5+QAAAACoEi1aJV1+M6nafLdiZ3x4\nZ+mW94snJONHVXY+oMEJuwGAaeLHleU33VTsjC22SF57LTn22KRt28rOBwAAAECVaj930vPqZIPH\nk1mWKX//xDHJy3+aVG1+e1JbW/ERgYYh7AYAKu6hhypTWX7rrclCC1V8PAAAAACagjlXS3oNTlY4\nv2C1+dvJo5snj/RJRr5R6emABiDsBgAq5oMPkh12SNZdt3hl+Z//rLIcAAAAgKnUolXS5aBStfmi\nuxc748O7Sre8XzhetTlUGWE3AFBv48YlZ5yRdO2a/P3vxc7YcstSZfnvf6+yHAAAAIAytZ87WeWq\nZIMnklmXLX//xLHJKycndy6ZvHebanOoEsJuAKBeHnwwWWaZ5IgjilWWd+6c3HNP8q9/qSwHAAAA\noJ7mXDXZaHDS44KC1ebvJI9tkTzcW7U5VAFhNwBQyAcfJNtvn6y3XulGdrlmmCE55ZTkxReTDTes\n/HwAAAAANFMtWiadD0z6DksW3aPYGR/1V20OVUDYDQCUZezY5K9/Tbp0Sf7xj2JnbLVVKSA/5hiV\n5QAAAABMI+3mSlb5W7LBk8msy5W/X7U5NHrCbgBgqj3wQKmy/Mgjk2+/LX//95Xl//xnsuCClZ8P\nAAAAACYzZ89ko6eTHhcmrWcpf/8P1eabJCNer/h4QHHCbgDgF73/frLddsn66ydDhpS/f4YZklNP\nVVkOAAAAwHTSomXS+YBJ1eZ7Fjvjo7uTu7olLxybjC9wEwSoOGE3ADBFY8cmp5+edO2a3HxzsTO2\n3roUkB99tMpyAAAAAKazdnMmq1xZz2rzU5J+Sybv3araHKYzYTcAUKf77y9Vlh91VLHK8i5dknvv\nTW65JVlggcrPBwAAAACFfV9tvuJFxarNR72bPLZV8vDGyYhhFR8PmDrCbgDgJ957L9l222SDDYpX\nlv/lL6XK8g02qPx8AAAAAFARLVomi+9fqjb/1V7FzvjonuSu7qrNYToRdgMASUqV5aedVqosv+WW\nYmdss00pID/qqKRNm8rOBwAAAADTRLs5k5WvSDYckMy6fPn7f6g2XyJ591+qzaEBCbsBgNx3X7L0\n0qXnao8aVf7+rl1LZ9x8s8pyAAAAAKrUHKskGw1KVrw4aTNr+ftHvZc8vnXyUC/V5tBAhN0A0Iy9\n917pNvaGGyZDh5a/v0OH0m3wF15I1l+/8vMBAAAAQINq0TJZfL+kz7DkV78udsbH9yZ3dUue/71q\nc5jGhN0A0AyNHVt6rnbXrsk//1nsjG23LVWWH3mkynIAAAAAmph2cyQrX55s+FQy2wrl7584Lnn1\nVNXmMI0JuwGgmbn33qR79+SYY4pXlt9/f/KPfyTzz1/5+QAAAACg0Zhj5WTDgcmKl9Sz2nyjZESB\nakXgZwm7AaCZePfdZOutk402SoYVeGRQhw7J6aeXKsvXW6/y8wEAAABAo9SiZbL4vpOqzfdOUlP+\nGR/fl9zVPXn+6GTcNxUfEZorYTcANHFjxiSnnpossUTyr38VO2O77UqV5UccobIcAAAAgGaq3RzJ\nypdNqjbvUf7+ieOSV09L7lwiefcW1eZQAcJuAGjC7rmnVFn++98XqyxfYonkgQeSv/9dZTkAAAAA\nJEnmWKkUeK90adJmtvL3j3o/eXzb5KENk6+HVH4+aEaE3QDQBL37brLVVkmvXsnrr5e/v0OH5K9/\nTZ5/Pll33YqPBwAAAADVrUXLZLF9kr7DSj8Wqja/P+m/tGpzqAdhNwA0IWPGJKecknTtmtx6a7Ez\ntt8+GTo0OfxwleUAAAAA8LPazl664b3RwGS2Fcvf/+Nq83duVm0OZRJ2A0ATcffdpcryY49NRo8u\nf/+SSyYPPpjcdFMy33yVnw8AAAAAmqzZV0w2eipZ6bLi1eZPbJc8uEHy9WuVnw+aKGE3AFS5d95J\nttwy2XjjYpXlM86YnHFGqbJ8nXUqPh4AAAAANA81LZLF9p5Ubb5vClWbf/JActfSyXNHqTaHqSDs\nBoAqNWZM8uc/J0sskfz738XO2GGHUmX5YYclrVtXdj4AAAAAaJbazp6sdEmy0aBi1ea145PXTk/6\ndVVtDr9A2A0AVah//6Rbt+S444pXlj/0UHLjjcm881Z+PgAAAABo9mbvMana/PJSAF6u0R9MqjZf\nX7U5TIGwGwCqyNtvJ1tskWyySfLGG+Xvn2mm5MwzS5Xla69d4eEAAAAAgJ+qaZEs9uukz7Bksf1S\nrNr8wUnV5kck40ZWfESoZsJuAKgC332XnHxyqbL8ttuKnbHjjsmQIcmhh6osBwAAAIAG1Xa2ZKWL\nS9Xms69U/v7a8clrZ5Sqzd/+u2pzmETYDQCN3PeV5ccfXwq9y7XUUsnDDyc33KCyHAAAAACmq9l7\nJBsOSFa+omC1+YfJkzskD66XfP1q5eeDKiPsBoBG6u23k803L1WWv/lm+ftnmik566zkueeStdaq\n9HQAAAAAQCE1LZJf7VWqNl98/xSrNn8ouWsZ1eY0e8JuAGhkvvsu+dOfSpXlt99e7IyddkqGDk0O\nOURlOQAAAAA0Sm1nS1a8KOn1dDL7yuXv/0m1+U2qzWmWhN0A0IjceWepsvyEE4pVlnfrljzySHL9\n9ck881R+PgAAAACgwmZbIdnwyWTlK5O2c5S/f/SHyZM7Jg+smwx/pfLzQSMm7AaARuCtt5LNNkv6\n9CleWX722cmzzyZrrln5+QAAAACAaaimRfKrPZM+Q5PFD0ihavNPH076L5s8e7hqc5oNYTcATEff\nfZecdFKy5JLJf/5T7Iyddy5Vlh98sMpyAAAAAKhqbWdLVrww6TU4mX2V8vfXjk+GnJn066LanGZB\n2A0A00m/fslSSyV/+EOxyvLu3UuV5dddp7IcAAAAAJqU2ZZPNnwiWflvBavNP5pUbb6OanOaNGE3\nADSw//432XTTpG/f0l+Xq2PH5JxzVJYDAAAAQJNW0yL51R5J32HJ4geWfl6uTx9J+i+TPHtYMm5E\n5WeE6UzYDQANZPTo5I9/LFWW33FHsTN22aVUWf673yWtWlV2PgAAAACgEWoza7LiBclGg5M5epa/\nv3ZCMuSs5I4uyVs3qDanSRF2A0AD+L6y/MQTkzFjyt/fvXvy6KPJtdcmnTpVfDwAAAAAoLGbbblk\ng8eTVa5K2s5Z/v7vPk4G7Jw8sHYy/OWKjwfTg7AbAKah//63VFfet2/y1lvl7+/YMTn33FJl+Rpr\nVH4+AAAAAKCK1LRIFt096Ts06XxQwWrzR5P+yybPHKranKon7AaAaWD06NIt7iWXLN3qLmLXXUuV\n5b/9rcpyAAAAAOBH2sya9Dg/6fVMMseq5e+vnZAMPXtStfn1qs2pWsJuAKiwO+4oVZb/8Y/FKsuX\nXjp57LHkmmtUlgMAAAAAP2PWZZMNHktWuboe1ea7JPevlQx/qdLTwTQn7AaACnnzzaRPn2TTTYtV\nls88c3LeeckzzySrr175+QAAAACAJqimRbLobknfYUnn3xSrNv/ssaT/cskzhyRjv678jDCNCLsB\noJ5Gj07+8IfSbe477yx2xm67lSrLf/MbleUAAAAAQAFtZkl6nFeqNp9ztfL3105Ihp6T9FNtTvUQ\ndgNAQbW1yX/+U3ou90knFassX2aZ5PHHk6uvTuaeu+IjAgAAAADNzazLJus/lqxyTdJurvL3f/fJ\n/6rNv3qx4uNBJQm7AaCAN94oVZZvtlny9tvl75955uT885PBg5PVCnzIEgAAAABgimpqkkV3TfoM\nTTr/tni1+d3LJ88crNqcRkvYDQBlGDUqOeGEUmX5XXcVO2P33ZNhw5KDDlJZDgAAAABMQ21mSXqc\nm/R6Nplz9fL3105Ihp5bqjb/77WqzWl0hN0AMBVqa5Pbby9Vlv/pT8nYseWfseyyyRNPJFddlcxV\noD0IAAAAAKCQWZdJ1n806Xlt0q7A8xS/+yR5arfk/jWTr16o/HxQkLAbAH7BG28kvXsnm2+evPNO\n+ftnnjm54IJSZfmqq1Z8PAAAAACAX1ZTkyyyS6navMvvClabP16qNh/8u2Ts8IqPCOUSdgPAFIwa\nlRx/fKmyvH//YmfssUepsvzAA5OWLSs7HwAAAABA2drMnKxwTtLruYLV5hOTYedNqja/pvRzmE6E\n3QDw/9TWJrfdVqosP/nkYpXlyy2XPPlk8re/qSwHAAAAABqhWZeeVG1+XcFq80+Tp3ZXbc50JewG\ngB95/fVkk02SLbYoVlk+yyzJhRcmTz+d9OxZ8fEAAAAAACqnpiZZZOdJ1eYHJzUF6ik/e2JStflv\nVZvT4ITdAJBSZflxxyXduiV3313sjD33LFWWH3CAynIAAAAAoIq0mTlZ4exk4+eSOdcof3/txGTY\n+arNaXDCbgCatdra5N//TpZYIvnzn+tXWX7llcmcc1Z+RgAAAACABjFL92T9R5Ke1yftOpW///tq\n8/vWSL56vtLTwWSE3QA0W8OGJRtvnGy5ZfLuu+Xvn3XW5KKLVJYDAAAAAE1ITU2yyE5J36FJl0OK\nVZt//mRy9wrJ4N+oNmeaEnYD0Ox8+21y7LFJ9+7JPfcUO2OvvZKhQ5P991dZDgAAAAA0Qa07Jiuc\nlWz8fDLXmuXvr52YDLsguaNz8uZVqs2ZJoTdADQbtbXJrbeWKstPOaVYZfnyyycDBiRXXKGyHAAA\nAABoBmbplqz3cLLqDcWqzcd8lgzcM7lv9eTL5yo9Hc2csBuAZmHYsKRXr2SrrZL33it//6yzJhdf\nnAwalKyySuXnAwAAAABotGpqkoV3LFWbdz20YLX5gOSeHsnTByVjv6r8jDRLwm4AmrRvv01+//uk\nW7fk3nuLnfHrX5fC8v32U1kOAAAAADRjrTsmy585qdp8rfL3105MXr8wuaOLanMqQtgNQJNUW5v8\n61+lyvJTT03GjSv/jBVWSJ56Krn88mSOOSo/IwAAAABAVZqlW7LeQ8mqNybt5yl///fV5veulnz5\nbOXno9kQdgPQ5Awdmmy0UbL11sUqy2ebLbnkkmTgwGTllSs/HwAAAABA1aupSRbeIekzJOl6WLFq\n8y+eSu7ukTx9oGpzChF2A9BkfPttcswxSffuyX33lb+/pibZe+9SWL7vvirLAQAAAAB+UeuOyfJn\nJBu/kMy1doEDapPXL0ru6Jy8+TfV5pRF2A1A1autTf75z6Rr1+QvfylWWd6jR6my/LLLVJYDAAAA\nAJRtlqWS9R5MVr2pYLX558nAvZJ7V1VtzlQTdgNQ1YYMSTbcMNlmm+T998vfP9tsyaWXloLulVaq\n/HwAAAAAAM1GTU2y8PZJn6HJEocnNa3KP+OLgZOqzQ9IxnxZ+RlpUoTdAFSlb75Jjj46WXrp5P77\ny99fU5Pss08ybFjpR5XlAAAAAAAV0nqmZLm/Jpu8kMy9ToEDapPXL076dU7euEK1OVMk7AagqtTW\nJrfckiyxRHLaacUqy1dcMRk4sHSje/bZKz8jAAAAAABJZl4yWfeBZLW/J+3nLX//mC+SQXtPqjZ/\npvLzUfWE3QBUjSFDkg02SLbdtnhl+WWXlSrLV1yx8vMBAAAAAPD/1NQkC22X9BmSLHFEParNV0wG\n7a/anJ8QdgPQ6H3zTXLUUaXK8gceKH9/TU2y776lyvK9905a+F8/AAAAAICG1XqmZLnTJ1Wbr1vg\ngNrkjUtUm/MT/rgfgEartja5+eaka9fk9NOLVZavtFIyaFByySUqywEAAAAApruZl0zWvT9Z7R9J\n+/nK3/9DtXnP5IvBlZ+PqiLsBqBReu21ZP31k+22Sz74oPz9s8+eXH55MmBA0qNH5ecDAAAAAKCg\nmppkoW0nVZsfWbDafFByz0rJoP1KATjNkrAbgEZl5MjkyCNLleUPPlj+/pqaZL/9SpXlv/61ynIA\nAAAAgEar9YzJcqclm7yYzL1egQNqkzcuTe7onLxxuWrzZkgEAECjUFub/OMfpcryv/41GT++/DO+\nryy/+OJkttkqPyMAAAAAANPAzEsk696XrH5zsWrzsV8mg/ZJ7lkl+eLpys9HoyXsBmC6e/XVUmX5\n9tsnH35Y/v7ZZ0+uuEJlOQAAAABA1aqpSRbcplRtvuRRSYvW5Z/x5dPJPSsng/ZVbd5MCLsBmG5G\njkyOOCJZZpnileX771+qLN9rL5XlAAAAAABVr/WMybJ/STZ+Mem0foEDapM3LitVm79+aTJxQsVH\npPEQCwDQ4Gprk7//vVRZfsYZxSrLV145efrp5KKLVJYDAAAAADQ5M3dN1rk3Wf2WZIb5y98/9svk\n6f2Se1dJPh9U+floFITdADSoV15J1lsv2WGHYpXlc8yRXHll8uSTyQorVH4+AAAAAAAaiZqaZMGt\nk96vJUseXbDafHAp8B64T/Ld55WfkelK2A1Agxg5Mjn88GTZZZOHHip/f01NcsABydChyZ57qiwH\nAAAAAGg2Ws+YLHtqsslLSacNChxQm7x5edKvi2rzJkZUAMA0VVub3HRT0qVLcuaZxSrLV1klGTw4\nufBCleUAAAAAAM1Wxy7JOvdMqjZfoPz9P1Sbr5x8PrDy89HghN0ATDOvvJKss06y447JRx+Vv3/O\nOZO//S154olk+eUrPx8AAAAAAFXm+2rzPq8lSx5TsNr8mUnV5nurNq9ywm4AKm7EiOSww5Jllkke\neaT8/S1aJAceWKos32MPleUAAAAAAPw/rToky54yqdp8w2JnvHlF0q9z8volqs2rlPgAgIqprU1u\nvDHp2jU566xkQoF/N+jZs1RZfsEFyayzVn5GAAAAAACakI5dknXuTtb4V8Fq86+Sp/dP7llJtXkV\nEnYDUBEvv1yqLN9pp+KV5VddlTz+eLLccpWfDwAAAACAJqqmJllgy1K1+VK/T1q0Kf+Mr56dVG3+\n6+S7zyo/I9OEsBuAehkxIjn00GTZZYtXlh90UKmyfPfdVZYDAAAAAFBQqw7JMn8uVZvPs1GxM968\nMunXJRl2kWrzKiBSAKCQ2trkhhuSLl2Ss88uVlm+6qrJM88k55+vshwAAAAAgArp2DlZu3+yxq3J\nDAuWv3/sV8ngAydVmz9V+fmoGGE3AGV76aVk7bWTnXdOPv64/P1zzplcfXXy2GOlG+EAAAAAAFBR\nNTXJAltMqjY/th7V5j2Tp/ZSbd5ICbsBmGpff50cckjpmdqPPlr+/hYtkt/8Jhk2LNltN5XlAAAA\nAABMY61mSJY5Odnk5eLV5v/9W3JHZ9XmjZCYAYBfVFubXH99qbL8nHOKVZavtlqpsvy885JZZqn0\nhAAAAAAA8DM6Ll6/avNxwydVm6+YfD6w4uNRjLAbgJ/14ovJWmslu+ySfPJJ+fvnmiu55hqV5QAA\nAAAATGc/qTY/rmC1+XPJiCGVn41ChN0A1Onrr5ODD06WX74UVJerRYvkt79Nhg5Ndt219O8QAAAA\nAAAw3bWaIVnmT5OqzTcub+8cqyaL7DJt5qJswm4AfqK2NrnuulJl+bnnFqssX3315NlnS/tVlgMA\nAAAA0Ch1XDxZ+85kzduSDgv98tfXtEhWvLD0I42CXwkAfvDii8maa5ZuYhepLJ977uTaa5NHH02W\nWaby8wEAAAAAQEXV1CTzb5b0fjXpdvzPV5svfkAy67INNhq/TNgNQIYPT373u1Jl+eOPl7+/ZcvS\n/qFDS8/2VlkOAAAAAEBVaTVDsvRJSe9Xknk3mfz1tnMmS/+p4efiZwm7AZqx2trSTewuXZLzzqtf\nZfk55yQzz1zxEQEAAAAAoOHMtFiyVr9kzduTDgv/b32505M2s0yvqZiCVtN7AACmjxdeSA48MHni\niWL75547OeOMZKed3OQGAAAAAKAJqalJ5t806bRB8upfks8eSxbZdXpPRR2E3QDNzPDhyQknJBde\nmEycWP7+li2T3/wmOfFEN7kBAAAAAGjCWrVPlv5jUjsxqVGY3RgJuwGaiYkTk+uuS448Mvn002Jn\nrLFGKSTv3r2yswEAAAAAQKMl6G60hN0AzcDzz5cqy598stj+Tp1KleU77qiyHAAAAAAAaBx8DAGg\nCRs+vFQ5vsIKxYLuli2TQw5Jhg71bG4AAAAAAKBxcbMboAmaODG59tpSZflnnxU7Y801S5Xl3bpV\ndjYAAAAAAIBKEHYDNDHPPVeqLB8woNj+Tp2SM89MdtjBTW4AAAAAAKDxUmMO0ER89VVy0EFJjx7F\ngu6WLZNDDy1Vlns2NwAAAAAA0Ni52Q1Q5SZOTK65JjnqqOKV5WutlVxwgcpyAAAAAACgegi7AarY\ns8+WKsufeqrY/nnmKVWWb7+9m9wAAAAAAEB1UWMOUIW++qoUcq+4YrGgu2XL5LDDkiFDPJsbAAAA\nAACoTm52A1SRiROTq68uVZZ//nmxM9Zeu1RZvtRSlZwMAAAAAACgYQm7AapEfSvL5523VFm+3XZu\ncgMAAAAAANVPjTlAI/fll8kBByQ9ehQLulu1Sg4/vFRZ7tncAAAAAABAU+FmN0AjNXFictVVydFH\nF68sX2edUmX5kktWdjYAAAAAAIDpTdgN0Ag980ypsnzgwGL75503OeusZNtt3eQGAAAAAACaJjXm\nAI3Il18m+++frLhisaC7VavkiCNKleWezQ0AAAAAADRlbnYDNAITJyZ/+1upsvyLL4qdse66yfnn\nqywHAAAAAACaB2E3wHQ2eHCpsnzQoGL755uvVFm+zTZucgMAAAAAAM2HGnOA6eSLL5L99ktWWqlY\n0N2qVXLkkaXKcs/mBgAAAAAAmhs3uwEa2MSJyZVXJsccU7yyfL31SpXlSyxR2dkAAAAAAACqhbAb\noAE9/XSpsvzpp4vtn2++5Oyzk623dpMbAAAAAABo3tSYAzSAL75I9t03WXnlYkF369bJUUeVKss9\nmxsAAAAAAMDNboBpasKE/1WWf/llsTPWX79UWd61a2VnAwAAAAAAqGbCboBp5OmnkwMOSAYPLrZ/\n/vlLleVbbeUmNwAAAAAAwP+nxhygwj7/PNlnn1JleZGgu3Xr5Oijk9de82xuAAAAAACAKXGzG6BC\nJkxIrrgi+f3vi1eWb7BBqbK8S5fKzgYAAAAAANDUCLsBKmDQoFJl+TPPFNu/wAKlyvItt3STGwAA\nAAAAYGqoMQeoh88/T/beO1lllWJBd+vWyTHHlCrLPZsbAAAAAABg6rnZDVDAhAnJ5ZeXKsu/+qrY\nGRtumJx3nspyAAAAAACAIoTdAGUaODA58MD6VZafc06yxRZucgMAAAAAABSlxhxgKn32WfLrXxev\nLG/TpnQT/LXXPJsbAAAAAACgvtzsBvgFEyYkl12WHHts8cryjTYqVZZ37lzZ2QAAAAAAAJorYTfA\nz3jqqVJl+bPPFtu/4IKlyvLNN3eTGwAAAAAAoJLUmAPU4bPPkr32Snr2LBZ0t2lTugn+2muezQ0A\nAAAAADAtuNkN8CMTJiSXXloKqocPL3ZGr16lyvLFF6/oaAAAAAAAAPyIsBtgkgEDSpXlzz1XbP+C\nCybnnptstpmb3AAAAAAAANOaGnOg2fv002TPPZNVVy0WdLdpkxx3XKmy3LO5AQAAAAAAGoab3UCz\nNWFCcsklpaC6aGX5xhuXbnOrLAcAAAAAAGhYwm6gWXryyVJl+fPPF9u/0EKlkHvTTd3kBgAAAAAA\nmB7UmAPNyqefJnvskay2WrGgu23b5Pjjk1df9WxuAAAAAACA6cnNbqBZGD/+f5XlX39d7IxNNind\n5l5sscrOBgAAAAAAQPmE3UCT98QTpcryF14otn/hhUshd9++bnIDAAAAAAA0FmrMgSbrk0+S3XdP\nVl+9WNDdtm1ywgmlynLP5gYAAAAAAGhc3OwGmpzx45OLLy49W7toZXnv3qXb3L/6VWVnAwAAAAAA\noDKE3UCT8vjjpcryF18stn/hhZPzzitVlgMAAAAAANB4qTEHmoRPPkl22y1ZY41iQXfbtskf/lCq\nLBd0AwAAAAAANH5udgNVbfz45KKLSpXlI0YUO6NPn+Scc1SWAwAAAAAAVBNhN1C16ltZvsgipedy\nu8kNAAAAAABQfdSYA1Xn44+TXXctXlnerl1y4onJK68IugEAAAAAAKqVm91A1Rg/PrnwwuSEE4pX\nlvftW6osX3TRio4GAAAAAABAAxN2A1XhscdKleUvvVRs/6KLlirL+/Sp7FwAAAAAAABMH2rMgUbt\n44+TXXZJ1lyzWNDdrl3yxz+WKssF3QAAAAAAAE2Hm91AozR+fHLBBckf/lC8snzTTUuV5YssUtHR\nAAAAAAAAaASE3UCj8+ijpcryl18utn/RRZPzzkt6967sXAAAAAAAADQeasyBRuOjj5Kdd07WWqtY\n0N2uXXLSSaXKckE3AAAAAABA0+ZmNzDdjRv3v8rykSOLnbHZZsnZZ6ssBwAAAAAAaC6E3cB0Vd/K\n8l/9qlRZvskmlZ0LAAAAAACAxk2NOTBdfPhhstNOxSvL27dP/vSn0l5BNwAAAAAAQPPjZjfQoMaN\nS84/v1RZ/s03xc7YfPNSZfnCC1dyMgAAAAAAAKqJsBtoMA8/nBx0UPLKK8X2L7ZYqbJ8440rOhYA\nAAAAAABVSI05MM19+GGy447JOusUC7rbt09OPjl56SVBNwAAAAAAACVudgPTzLhxpZvYJ55YvLJ8\niy1KleULLVTR0QAAAAAAAKhywm5gmnj44eTAA5NXXy22f7HFSs/27tWromMBAAAAAADQRKgxByrq\ngw+SHXYoVZYXCbrbt0/+/Ofk5ZcF3QAAAAAAAEyZm91ARYwbl5x7bvLHPxavLN9yy+Sss1SWAwAA\nAAAA8MuE3UC9PfRQctBBxSvLF1+8VFm+0UaVnQsAAAAAAICmS405UNgHHyTbb5+su26xoHuGGZJT\nTkleeknQDQAAAAAAQHnc7AbKNnbs/yrLv/222BlbbVWqLF9wwcrOBgAAAAAAQPMg7AbK8sADpcry\nIUOK7e/cuVRZvuGGlZ0LAAAAAACA5kWNOTBV3n8/2W67ZP31iwXdM8yQnHpq8uKLgm4AAAAAAADq\nz81u4GeNHZucc05y0knFK8u33jo580yV5QAAAAAAAFSOsBuYovpWlnfpUqos32CDys4FAAAAAAAA\nasyBybz/frLttvWrLP/LX0qV5YJuAAAAAAAApgU3u4EfjB2bnH128qc/Fa8s32abUmX5AgtUdjYA\nAAAAAAD4MWE3kCS5//5SZfnQocX2d+mSXHBB6TY4AAAAAAAATGtqzKGZe++90m3sDTYoFnR36JCc\ndlqpslzQDQAAAAAAQENxsxuaqbFjk7POKlWWjxpV7Ixtty1Vls8/f2VnAwAAAAAAgF8i7IZm6N57\nk9/8Jhk2rNj+rl1LleXrrVfZuQAAAAAAAGBqqTGHZuTdd5Ott0422qhY0N2hQ3L66ckLLwi6AQAA\nAAAAmL7c7IZmYMyYUmX5yScXryzfbrvkjDNUlgMAAAAAANA4CLuhiatvZfkSSyTnn+8mNwAAAAAA\nAI2LGnNoot59N9lqq/pVlv/1r8nzzwu6AQAAAAAAaHzc7IYmZsyY5MwzS5Xlo0cXO2P77UuV5fPN\nV9nZAAAAAAAAoFKE3dCE3HNPqbL89deL7V9iieTCC5N11qnsXAAAAAAAAFBpasyhCfi+srxXr2JB\n94wzlm5yv/CCoBsAAAAAAIDq4GY3VLExY0oh9Z//XLyyfIcdSs/mVlkOAAAAAABANRF2Q5W6++5S\nZfkbbxTbv+SSpcrytdeu6FgAAAAAAADQINSYQ5V5++1kiy2SjTcuFnTPOGNy5pnJ888LugEAAAAA\nAKhebnZDlfjuu1Jl+SmnFK8s33HHUmX5vPNWdjYAAAAAAABoaMJuqAL9+ye//W3xyvKllkouuMBN\nbgAAAAAAAJoONebQiL39drL55skmmxQLumeaKTnrrOS55wTdAAAAAAAANC1udkMj9N13pbrxU04p\n/XURO+1UOmOeeSo7GwAAAAAAADQGwm5oZO66q1RZ/uabxfZ361aqLF9rrcrOBQAAAAAAAI2JGnNo\nJL6vLO/du1jQPdNMydlnJ88+K+gGAAAAAACg6XOzG6az775LTj89OfXU4pXlO+9cOkNlOQAAAAAA\nAM2FsBumozvvLFWW//e/xfZ3716qLF9zzcrOBQAAAAAAAI2dGnOYDt56K9l006RPn2JBd8eOyTnn\nlCrLBd0AAAAAAAA0R252QwMaPbpUN/6XvxSvLN9ll9IZnTpVdjYAAAAAAACoJsJuaCD9+iW/+139\nKssvvDBZY43KzgUAAAAAAADVSI05TGP//W/St2/pP0Ury889t1RZLugGAAAAAACAEje7YRoZPTo5\n7bRSZfmYMcXO2HXX0hkqywEAAAAAAOCnhN0wDdxxR6my/K23iu1feulSZfnqq1d2LgAAAAAAAGgq\n1JhDBX1fWb7ppsWC7o4dk/POS555RtANAAAAAAAAP8fNbqiA0aNLdeWnnVa8sny33Ur75567srMB\nAAAAAABAUyTshnqorf1fZfnbbxc7Y5llSpXlq61W0dEAAAAAAACgSVNjDgW9+WbSp0+y2WbFgu6Z\nZ07OPz8ZPFjQDQAAAAAAAOVysxvKNGpUqbL89NOLV5bvvnvpDJXlAAAAAAAAUIywG6ZSbW3yn/8k\nBx9cvLJ82WVLleWrrlrBwQAAAAAAAKAZUmMOU+GNN5LevZPNN69fZfnTTwu6AQAAAAAAoBLc7Iaf\nMWpUcuqppcrysWOLnbHHHqXK8rnmquxsAAAAAAAA0JwJu6EOtbXJ7beXKsvfeafYGcsum1x0UdKz\nZyUnAwAAAAAAABI15jCZ7yvLt9iiWNA9yyyl53IPHizoBgAAAAAAgGlF2A2TjBqVHHdcstRSSf/+\nxc7Yc89k6NDkgAOSli0rOx8AAAAAAADwP2rMafZqa5PbbitVlr/7brEzlluudJvbTW4AAAAAAABo\nGG5206y9/nqy8cbJllsWC7pnmaX0XO6nnxZ0AwAAAAAAQEMSdtMsffttcuyxSbduyT33FDtjr72S\nYcOS/fdXWQ4AAAAAAAANTY05zUptbfLvfyeHHFK8snz55UuV5ausUtnZAAAAAAAAgKnnZjfNxrBh\nSa9eyVZbFQu6Z521VFk+aJCgGwAAAAAAAKY3YTdN3rffJr//famy/N57i53x61+rLAcAAAAAAIDG\nRI05TVZtbXLrraXK8vfeK3bGCiuUKstXXrmyswEAAAAAAAD142Y3TdL3leVbb10s6J511uSSS5KB\nAwXdAAAAAAAA0BgJu2lS6ltZXlOT7L13KSzfd1+V5QAAAAAAANBYqTGnSaitTf71r+TQQ4tXlvfo\nUaosX2mlys4GAAAAAAAAVJ6b3VS9IUOSDTdMttmmWNA922zJpZcmTz0l6AYAAAAAAIBqIeyman3z\nTXL00cnSSyf331/+/pqaZJ99SpXl++yjshwAAAAAAACqiRpzqk5tbfLPf5Yqy99/v9gZPXokF12U\nrLhiZWcDAAAAAAAAGoab3VSV7yvLt922WND948pyQTcAAAAAAABUL2E3VeGbb5KjjqpfZfm++6os\nBwAAAAAAgKZCjTmN3kMPJbvsknzwQbH9K65Yqizv0aOycwEAAAAAAADTj5vdNHpzzpl8/HH5+2af\nPbn88lJluaAbAAAAAAAAmhZhN41et27Jb3879V9fU5Pst18ydGjy618nLXyXAwAAAAAAQJMjBqQq\nnHhi0qnTL3/dSislgwYlF19cutkNAAAAAAAANE3CbqpCx47JGWdM+fXZZ0+uuCIZMEBlOQAAAAAA\nADQHwm6qxo47Jmuu+dO1mppk//2TYcOSvfZSWQ4AAAAAAADNhWiQqlFTk1xwQdKyZennK6+cPP10\nctFFyWyzTd/ZAAAAAAAAgIbVanoPAOXo3j054YRkvvmSPfZwkxsAAAAAAACaK2E3VeeEE6b3BAAA\nAAAAAMD05l4sAAAAAAAAAFVH2A0AAAAAAABA1RF2AwAAAAAAAFB1hN0AAAAAAAAAVB1hNwAAAAAA\nAABVR9gNAAAAAAAAQNURdgMAAAAAAABQdYTdAAAAAAAAAFQdYTcAAAAAAAAAVUfYDQAAAAAAAEDV\nEXYDAAAAAAAAUHWE3QAAAAAAAABUHWE3AAAAAAAAAFVH2A0AAAAAAABA1RF2AwAAAAAAAFB1hN0A\nAAAAAAAAVB1hNwAAAAAAAABVR9gNAAAAAAAAQNURdgMAAAAAAABQdYTdAAAAAAAAAFQdYTcAAAAA\nAAAAVUfYDQAAAAAAAEDVEXYDAAAAAAAAUHWE3QAAAAAAAABUHWE3AAAAAAAAAFVH2A0AAAAAAABA\n1RF2AwAAAAAAAFB1hN0AAAAAAAAAVB1hNwAAAAAAAABVR9gNAAAAAAAAQNURdgMAAAAAAABQdYTd\nAAAAAAAAAFQdYTcAAAAAAAAAVUfYDQAAAAAAAEDVEXYDAAAAAAAAUHWE3QAAAAAAAABUHWE3AAAA\nAAAAAFVH2A0AAAAAAABA1RF2AwAAAAAAAFB1hN0AAAAAAAAAVB1hNwAAAAAAAABVR9gNAAAAAAAA\nQNURdgMAAAAAAABQdYTdAAAAAAAAAFQdYTcAAAAAAAAAVUfYDQAAAAAAAEDVEXYDAAAAAAAAUHWE\n3QAAAAAAAABUHWE3AAAAAAAAAFVH2A0AAAAAAABA1ampra2tnd5DNHULLbRQxo8fnxYtWmSuueaa\n3uMAAAAAAAAATDdzzTVX+vfvX+9zWlVgFn7BxIkTf/jx448/ns7TAAAAAAAAAFQ/YXcDaNu2bcaM\nGZOWLVtm9tlnn97jAAAAAAAAAEw3lWrDVmMOAAAAAAAAQNVpMb0HAAAAAAAAAIByCbsBAAAAAAAA\nqDrCbgAAAAAAAACqjrAbAAAAAAAAgKoj7AYAAAAAAACg6gi7AQAAAAAAAKg6wm4AAAAAAAAAqo6w\nGwAAAAAAAICqI+wGAAAAqGJnnnlm5ptvvsn+AwAA0NS1mt4DAAAANJQzzzyzzvXDDjusgScBAAAA\noL6E3QAAQLNx1lln1bku7AYAAACoPsJuAAAAmMa+/vrrXHHFFZOtb7TRRunWrdt0mAgAAACqn7Ab\nAAAAprERI0bU2Sww//zzC7sBAACgoBbTewAAAAAAAAAAKJewGwAAAAAAAICqo8YcAAAAoIoddthh\nOeyww6b3GAAAAA3OzW4AAAAAAAAAqo6wGwAAAAAAAICqI+wGAAAAAAAAoOoIuwEAAAAAAACoOq2m\n9wAAAAAkEydOzFNPPZVHH300L7zwQt5555188cUXGT16dFq3bp2ZZpop888/f7p27ZqVV145G2yw\nQWaZZZZpPtdXX32Vp556KkOHDs1nn32WMWPGZIYZZsgcc8yRzp07Z+WVV86ss846zeeYFoYPH577\n7rsvL774Yl555ZV8+OGHGTlyZL799tvU1NSkffv2ad++feaee+7MP//8WWihhbL00ktn+eWXz3zz\nzfezZ3/55Zc56aSTfvj5t99+W+fX3XTTTRkwYMBUzbvYYovloIMOmvq/wf/nueeey2OPPZbnnnsu\nb7/9dj799NOMGjUqtbW16dChQ+aZZ5506dIlK620UjbaaKN06tSp8HsV9eWXX2bgwIF5/fXX8/nn\nn2fUqFFp165d5p577nTt2jU9e/bMjDPO2OBzFfHMM8/kiSeeyCuvvJLXX389w4cPz8iRIzNmzJi0\nbds27du3T8eOHTP//PNngQUWSOfOnbPccsulW7duadeuXYPNedJJJ+XLL7+c5u9z0EEHZbHFFiu8\nf9SoUXnooYcycODAvPrqq3n33XczfPjwjB49Om3atMkss8ySBRdcMN27d8/qq6+etddeO23atKng\n3wEAANAY1dTW1tZO7yEAAAAawpQCyg8++KCBJ/mf0aNH55prrsnll1+ejz/+eKr3tW7dOn369Mnv\nfve7LL744hWf64knnsgll1yShx9+OBMnTpzi17Vs2TKrr7569ttvv6y55po/eW2XXXaZ7O9pww03\nzBFHHFHxecsxdOjQnHHGGbn//vszduzYQmcsvPDC6dOnT3baaacsuOCCk73+3nvvZZVVVqnvqD/R\ns2fP/POf/yxrz+jRo3P99dfnb3/7W959992p3teiRYtssMEGOfTQQ9OtW7dyR/3BwQcfnFtuueUn\na/PPP38GDhz4k7WHH344l1xySZ588slMmDBhiue1bt06G220UQ466KB079698FzTyvjx43PVVVfl\n6quvzttvv13ojLZt22bttddO3759s8UWW0zVnjPPPDNnnXXWZOtT88+2lVdeOe+//37Zc5brlltu\nyaqrrlr2vjfeeCMXX3xxbr/99owePXqq980yyyzZY489st9++1XNByQAAIDyudkNAAAwnTzxxBM5\n/PDDywohvzdu3Lj8+9//Tr9+/bL//vvn8MMPT8uWLes901dffZWjjjoqd95551R9/YQJE/LII4/k\nkUceySabbJLTTz/9h5vew4YNmyxEW2qppeo9Y1G1tbU57bTTcvHFF2f8+PH1Ouvtt9/OBRdckJlm\nmqlet62npXvvvTfHHntsPvzww7L3Tpw4Mffcc0/uv//+7LvvvjnqqKPSqlXl/wjhyy+/zOGHH557\n7rlnqr5+3Lhx6devX+68887stttuOf744xv0FvTPefXVV/Ob3/wmQ4YMqdc5Y8aMyT333JOHH354\nqsPupui7777LX//611xxxRWFfr8OHz48Z599dm666aacffbZk30YBwAAaBo8sxsAAGA6uPrqq7PD\nDjsUCrp/bNy4cTnvvPOy44475ptvvqnXWW+99VZ69+491UH3/3fXXXdls802m6435adk4sSJOeSQ\nQ3L++efXO+hu7Gpra/PnP/85e+yxR6Gg+8cmTJiQiy66KDvttFNGjRpVoQlLPvjgg2y66aZTHXT/\nWG1tba6++upsueWWDVLB/Uuef/75bLPNNvUOuin54IMPsvnmm+eSSy6p9+/Xjz/+ODvvvHOuvvrq\nygwHAAA0Km52AwAANLBrrrkmxx577M9+TadOnbLIIotkrrnmysiRI/PRRx9l6NChU6wUf/zxx7Pz\nzjvn73//e6Gbrh9++GG22WabfPTRR2Xv/bE333wzu+66a26//fZ6nVNpl1566WR12j/WokWLLLjg\ngllooYUy44wzpm3bthk1alRGjhyZTz75JG+99dbP1ms3FrW1tTnssMPyj3/842e/br755stCCy2U\nWWedNS1atMjnn3+eoUOHTjE4fvzxx7PnnnvmxhtvTIsW9f/c/IgRI7Lzzjvnrbfeqtc5L7zwQrbb\nbrvceuutmWmmmeo9VxEjR47MnnvumeHDh0/xa2aeeeYsssgimXvuuTPDDDNk4sSJGTlyZL7++uu8\n+eabP7u3uXnvvfeyzTbb5L333pvi17Rs2TJdu3bNXHPNlZlnnjnffvttPvvss7zyyisZN27cZF8/\nYcKEHHvssZlhhhmy7bbbTsvxAQCABibsBgAAaEADBgzICSecMMXXe/funb333js9evRITU3NT177\n5JNPcuutt+bcc8/NyJEjJ9v79NNP5+ijj84555xT1kwTJ07MfvvtN8Wge5ZZZknfvn2zySabZNFF\nF82cc86Zb7/9Np988kkGDBiQ22+/PYMHD/7h64cMGZITTzyxrBmmpY8//rjO5xknSefOnbP//vtn\ngw02+KF+vS5jxozJ0KFD8/DDD+e+++7Lc889l9ra2il+/QILLPCTG+5Teob3WWedle22266Mv5uf\n95e//GWKQXenTp2y1157pW/fvllggQUme33ixIl57rnncuGFF9Z52/qxxx7Leeedl4MPPrjecx5/\n/PEZNmzYT9aWXXbZbLnllll11VXTqVOntGvXLp988kmGDh2a//znP+nfv3/GjBkz2VmvvvpqDj/8\n8Fx66aX1nquIM844I5988slk623atMl2222XHXfcMd27d5/s9/OPffTRR3n22Wdz33335YEHHmjQ\n2+r///np9XHzzTfnkEMOqfO1jh07/uL+7z8EMaWgu2fPnvn1r3+d1Vdfvc7ncI8cOTJ33313zj77\n7LzzzjuTvX7sscdm+eWXz2KLLfaLswAAANWhpvbn/t85AABAEzLffPPVud5QtdujR4/OOuusU2eQ\n0759+5x33nnZZJNNfvGcDz74IPvtt1+effbZOl+/6qqrsuGGG071XFdccUX+8Ic/1Pla3759c/LJ\nJ2eOOeb42TNuv/32HH/88fniiy9+WGvduvVktyy32WabssP4+rrsssvyxz/+cbL1rbbaKmeccUba\ntGlT9plvvfVWrrzyyiy22GLZfffdf/HrGyLsfvjhh7PTTjvV+dpuu+2WP/zhD2nbtu1UnXXvvffm\nwAMPnKy6vFWrVvn3v/+d5ZdffqrOOfjggye7Ud+qVaufVFN37NgxJ5544i/+9/D666/nkEMOyXPP\nPVfn61deeWV69eo1VXNVyvjx47Psssvmq6+++sl6x44dc/3112eFFVYo+8xx48bljjvuyHXXXZd/\n//vfU7XnzDPPrPMDHQ35SIHHHnssu+yyS503q4844oip+pDEAQccUGcrxCyzzJKzzz57qv+5Nnbs\n2BxzzDH5+9//Ptlr3bp1y5133jlNnkEPAAA0PM/sBgAAaCCXXHJJnUF3mzZtcsUVV0xV0J2UQvvr\nr78+SyyxRJ2vn3DCCVP9nNuPPvoop512Wp2v7b777rnkkkt+MehOks022yz//Oc/M9tss/2wVlfo\nNT3cd999k60tvPDChYPuJFlkkUVy8sknT1XQ3RC+++67HHnkkXW+9uc//zmnnHLKVAfdSbLhhhvm\nxhtvTOvWrX+yPn78+Pz1r3+t16w//t7s0KFDbrzxxqkK/BdffPHccsstWXnllet8/fe//329n1tf\nrsGDB08WdCel34NFgu6k9CGRLbfccqqD7sZgyJAh2Weffer8Pb/99ttPVdD9wAMP1Bl0zznnnLnz\nzjvL+gBPmzZtcuaZZ2a33Xab7LWXX345d9xxx1SfBQAANG7CbgAAgAYwevToXHHFFXW+dthhh2Xt\ntdcu67yZZ545V111VZ3P537vvfdy6623TtU5N9xww2S3d5Nk7bXXzsknn1zWTJ07d86VV175s3XN\n00NddcZ9+/YtHHQ3Rtdcc02dt3j33nvvwoH8iiuumGOOOWay9UcffTRDhgwpdOb/d8EFF2S55Zab\n6q9v3759rr766sw///yTvfbJJ5/87HPZp4W6vrdatWqVzTffvEHnmJ4++eST7LLLLhkxYsRkr621\n1lpT/DDNj9XW1uYvf/nLZOutW7fONddck4UXXrjQbCeeeGKWXnrpydYvv/zyQucBAACNj7AbAACg\nAdx5550ZPnz4ZOuLLrpo9tlnn0JnLrDAAjnooIPqfO2GG274xf0TJkzITTfdNNl627Ztc/LJJxcK\nrVdaaaVsu+22Ze+blj7//PPJ1qZUaV+NJk6cmCuvvHKy9U6dOuWoo46q19l77rln5p133snWr7rq\nqnqdm5Ruj5dzW/d7HTt2nOJz76+//vr6jlWWzz77bLK12WabLe3bt2/QOaaXb7/9Nrvuums+/PDD\nyV5bYoklcumll05VXfhjjz2WV199dbL13XbbLcsss0zh+dq0aVNn48ELL7yQZ555pvC5AABA4yHs\nBgAAaAD9+vWrc33vvfeu1w3jvffeu87b3YMHD64zgPqxRx55JB9//PFk61tuuWUWWWSRwjMdeuih\njep2d11hW10BeLV6/PHH67zVfcABB9Q7dG3dunV23nnnOt+zvqZUuz41evfunW7duk22PmTIkAYN\nMev63hoxYkTGjh3bYDNMLxMmTMh+++2Xl19+ebLXOnXqlGuvvTYzzTTTVJ118803T7bWunXr/O53\nv6v3nOuss06d/zx77LHH6n02AAAw/Qm7AQAAprHx48dnwIABk623adMmm266ab3OnnHGGbPxxhvX\n+dovhTkDBw6sc33LLbes10zzzz//FJ+rPD3MOeeck63deuutTSaQvPfeeydba9GiRfr27VuR81df\nffXJ1t5+++06bzVPrSWXXHKKz5yfWltttVWd608++WS9zi3HXHPNNdnad999V1XP2y7qmGOOyYMP\nPjjZ+owzzphrr722zkaAukyYMKHOc9ZYY43MNtts9Z4zSVZbbbXJ1gYPHlyRswEAgOlL2A0AADCN\nvfHGG/nmm28mW+/Ro0dmmWWWep8/pSro559//mf31fX6zDPPnJ49e06zmaaHFVZYYbK1//73v9ln\nn33y5ZdfToeJKquuD1IsueSSdQaxRXTv3r3O9fqEhb179y6895fOeO655+p99tSq63srSY477rjc\nddddDTZHQ7vgggvqfFRCq1atcumll2appZaa6rNeeeWVfP3115Otr7322vUZ8Sfqem63GnMAAGga\nhN0AAADT2NChQ+tcn1KIWK4pnTOl902S2travPDCC5OtL7nkkhWpIC8n7JrW+vTpU+f6fffdl9VW\nWy0nnnhinVXM1eC7777L66+/Ptl6586dK/Yebdq0qbOO+pdq8n9OXeFjueabb77MPvvsk603ZNi9\n0EIL1fn7b9SoUdl7772z+eab55///GdGjBjRYDNNa7fffnv+8pe/1PnaqaeeWnZI/dJLL9W5vvji\ni5c72hTVdUN8xIgRGTlyZMXeAwAAmD4mf7gUAAAAFVXX85ST1LvG+XsLL7xwOnTokG+//Xaq3jdJ\nRo4cWWfQs+SSS1ZkpkqdUwkbbrhhlltuuTpD0BEjRuTyyy/P5ZdfnnnnnTerr756evbsmRVXXLFe\nzy1vKO+++24mTJgw2fprr72Wgw8+uGLvM378+MnWhg8fXvi8Sn0YYqmllsqjjz76k7VPP/00o0aN\nygwzzFCR9/glRxxxRHbdddc6X3v66afz9NNPp3Xr1unRo0dWXXXVrLzyylluueUabL5KGjhwYA45\n5JDU1tZO9tpvf/vb7LjjjmWf+dZbb9W5fu211+bWW28t+7y6fPrpp3WuDx8+fKqfKw4AADROwm4A\nAIBpbErPNp5jjjkqcn5NTU1mn332ycLun3umcl21wUnqvClbxGyzzZaWLVvWGcRODxdffHF69+6d\nL774Yopf8+GHH+bmm2/OzTffnKT069OzZ8+suuqqWXvttbPgggs21LhT7aOPPqpz/bXXXstrr702\nTd+7aNjdokWLzD333BWZYUrnfP311w0WJq+33nrZf//9c/HFF0/xa8aNG5cBAwb8UDnfqlWrdOvW\nLauuumpWW221rLbaamndunWDzFvUG2+8kT333DNjxoyZ7LUtt9wyRx55ZKFzp/Q93L9//0LnlWP4\n8OFZYIEFpvn7AAAA044acwAAgGls1KhRda7POOOMFXuPum4njhkzZoph85TC7krOVMmz6muBBRbI\nHXfcUdaN888//zx33HFHjjnmmPTs2TObbbZZbrjhhowdO3YaTlqe6VmPXddz6KdGJb8vOnbsWOf6\nlL6/p5Xjjjsuxx13XFq2bDlVXz9+/Pg8//zzueiii7LTTjtl2WWXzdFHH/2zjx6Ynj7//PPsuuuu\ndX7AoWfPnjnzzDMLP/6gGr+HAQCAxkPYDQAAMI2NGzeuzvVK3jyd0llTCmanFMA3xEzTy0ILLZT+\n/fvnlFNOyTzzzFP2/sGDB+fII4/M6quvnttuu63yAxZQ1y3bhlJXlfXU6NChQ8VmmNJZ0+NZzPvv\nv38efPDB9O7de6pD7+8NHz481113XdZff/0ceOCB+fzzz6fRlOUbPXp0dt9997zzzjuTvbb44ovn\nyiuvTJs2bQqfX43fwwAAQOMh7AYAAJjGplRPPKXAuYgpnTWlEGpKQfTo0aMrNlMlz6qUVq1aZbfd\ndsugQYNy4403Zvvtty+7xviDDz7IgQcemCOPPDITJ06cRpNOnXJD1cagkuHmlM5q165dxd6jHIst\ntlguu+yyDBo0KMcdd1xWXXXVsmaZOHFibrvttmy44YZ1PmO+oU2cODEHHXRQnbPMOeecue666zLz\nzDPX6z2q8XsYAABoPDyzGwAAYBqbUrBcyQrdum6ytm3bdopB0pQCqkreiJ0et2unVosWLbLWWmtl\nrbXWSpK8//77eeqppzJo0KA89dRTefPNN3/xjBtuuCEdOnTIH/7wh2k97hRN6XvrgAMOyLHHHtvA\n00ydSn7fT+ms+gaw9dWpU6fsv//+2X///TNmzJg8++yzGThwYAYNGpRnnnnmF/87+OSTT7Lrrrum\nX79+WWihhRpo6smdeOKJufvuuydbb9++fa655pqKPO96St/DDz/8cBZffPF6nw8AADRtwm4AAIBp\nbM4556xz/YsvvqjI+bW1tXWeNaX3Tab8rONKzfTVV19N8XnhjdH888+frbfeOltvvXWS0jOKH374\n4dx77725//77p3iD+LLLLssWW2yRpZdeuiHH/cGUfo3rerZyYzF27NiMGjWqIjX3X331VZ3rU/r+\nnh7atm2bnj17pmfPnkmSCRMm5IUXXsh9992XO++8c4ofrPjyyy9zwgkn5JprrmnIcX9w+eWX58or\nr5xsvWXLlrnooouyzDLLVOR9qvF7GAAAaDzUmAMAAExj8803X53rr776akXOf/vtt/Ptt99O9fsm\npTBwpplmmmYzVeqc6WWOOebI1ltvncsuuyxPP/10DjjggLRqVffnxS+88MIGnu5/pnTr97PPPmvg\nScozZMiQaXZOu3btGlXY/f+1bNkyyy+/fI466qg8+uijuemmm9K1a9c6v/b+++/PsGHDGnjCpH//\n/jnppJPqfO2kk07KhhtuWLH3qtbvYQAAoHEQdgMAAExjXbp0qXP95Zdfrsj5UzpnSgFaktTU1NR5\nG/nVV19NbW1tvWd65ZVX6n1GYzH77LPn2GOPzQUXXFDn64899th0u8U+++yzZ5555plsvTE87/nn\nVOL7Y/To0Xn77bcnW+/WrVtatKieP+5Yc801c8cdd2TZZZet8/WHHnqoQed59tlnc9BBB9X5PPp9\n9903u+++e0Xfr1u3blOcAwAA4JdUz//7AwAAqFKLLbZYnbeoBw8enK+//rre59977711rk8pPPve\ncsstN9na119/nQEDBtR7pnvuuafeZzQ2ffv2zZprrjnZ+tdff50PPvjgZ/e2bt26zvVKhOQrr7zy\nZGuff/55xW5PTwuPPPJIvc949NFH6wxk6/q+buxmmGGGnHjiiXW+1pAtCe+880523333fPfdd5O9\n1rt37xx//PEVf8/ll18+bdq0mWz9iSeeqPh7AQAATY+wGwAAYBpr1apVVl111cnWx4wZkzvuuKNe\nZ3/77bfp379/na+tscYaP7u3rpA0SW699dZ6zfT+++9n4MCB9Tqjsaor7E5++VnnM844Y53ro0eP\nrvdMvXr1qnP9hhtuqPfZ08qDDz5Y7w96/Otf/6pzvUePHvU6d3rp0aNHnc8x//LLLxvk/b/66qvs\nvPPOdX4vr7DCCjnvvPNSU1NT8fft0KFDVl999cnWX3zxxbz00ksVfz8AAKBpEXYDAAA0gD59+tS5\nfvnll2fcuHGFz73yyivrDExXWmmlOuutf2yttdZKp06dJlu/9dZb66yHnlpnnXVWRarQG6MOHTrU\nuT6lm9s/3ldXUPjxxx/Xe6YNNtggs80222TrN954Y0XOnxbGjBmTa665pvD+d955J/fff/9k6zPP\nPHPWW2+9+ow23dTU1NT5/fVL31uVMGbMmOy5557573//O9lrCy+8cK6++uq0a9dumr3/9ttvX+f6\nmWeeOc3eEwAAaBqE3QAAAA1g4403zqyzzjrZ+htvvJErrrii0JkffPBBzjvvvDpf23HHHX9xf8uW\nLbPDDjtMtj5mzJgce+yxhQLrp59+OjfffHPZ+6rFW2+9Ved6XR8a+LGampossMACk61Xomq8Xbt2\n2WOPPSZb/+6773LAAQdk7Nix9X6PaeH888/PRx99VGjviSeemDFjxky2vtVWW6V9+/b1HW26+Prr\nr+u8VT333HNP0/etra3NwQcfnEGDBk322myzzZbrr7++zg9TVFKvXr2y8MILT7Z+33335dprr52m\n7w0AAFQ3YTcAAEADaN++ffbee+86X/vrX/+axx57rKzzRo4cmT333LPOW90LLbRQtthii6k6Z6ed\ndqqzOvnhhx8u+/m8w4YNy5577tmobnW/9tprueqqqypSFz5ixIjcdtttk63PM888mX322X9xf7du\n3SZbe+KJJ/LJJ5/Ue7b99tuvzsB94MCBOfjgg+t8BnMRtbW1eeCBB/LCCy/U+6xRo0Zl3333LfvX\n5rLLLqvzOfUtWrTILrvsUu+5ynHppZdWrGr7+uuvr/MZ5N27d6/I+VNyyimn5D//+c9k6+3atcvf\n/va3LLLIItP0/ZPSB2+m9M+b448/vt6Pe/ixESNG5PLLL6/YeQAAwPQl7AYAAGgg++yzTxZccMHJ\n1seMGZO99tor99xzz1Sd8+GHH2bnnXfOyy+/XOfrJ554Ylq1ajVVZ80zzzw56qij6nztqquuyv77\n7/+Lz6NOkjvuuCPbbLPNT54v3BD1y7/kq6++ynHHHZcePXrktNNOy5tvvlnonBEjRmSfffbJp59+\nOtlrm2+++VQ9y7iuZ6R//2tf3xveM8wwQ84888w657j99tvTt2/fvPbaa4XP//LLL3Pttddm7bXX\nzq677lqvmvsfe+aZZ7LHHntM1fdYbW1tLrvsspx00kl1vr7nnnumc+fOFZlrat13333p1atXttlm\nm9x1112FP1TQv3//nHHGGZOtt2nTJptsskl9x5yif/zjH7nooosmW6+pqcm5556bFVdccZq99//X\nq1evbL755pOtjx8/Pvvtt19OOOGEfPPNN4XPf/XVV3PCCSekR48eOfXUU+sxKQAA0JjU1Damj9wD\nAABMQ/PNN1+d69tss03F32uxxRbLQQcdNNn6wIEDs+2222b8+PF17tt0002z1157pUePHpO99umn\nn+bWW2/NueeemxEjRtS5f/vtty/7ObcTJ07M5ptvnmeeeabO12eZZZZsttlm6dWrV371q19ljjnm\nyKhRo/LJJ59kwIABue222zJ48OCf7Nlhhx3y2GOP5f333//J+jbbbJNzzjmnrPnq48knn5zs13eJ\nJZZInz59stJKK6Vbt27p2LHjFPd//PHHueOOO3LJJZfU+fzrmWaaKQ888MAUv7d+7Msvv8wKK6ww\nxVrxhRZaKL/61a/SsWPHOj8oMKXvqR8799xzc/rpp9f5Wk1NTdZZZ53svPPOWXnllTPLLLNM8ZzR\no0fn1VdfzXPPPZd77rknAwcOzIQJE354/aKLLspmm232s7MkycEHH5xbbrnlJ2tzzTVXZppppp98\n8GC22WbLYYcdlk033XSyyuwJEybkiSeeyHnnnZcBAwbU+T4LLrhgHnzwwQavMN96661/MlOHDh2y\nwQYbZL311ssyyyyTRRdddIofhBg/fnwGDRqUq666Kv3796+zEeHXv/51/vjHP/7iHGeeeWbOOuus\nydY/+OCDn91X169PUqrlX2ONNX7xfctx0EEHZbHFFvvZr/nmm2+y1VZbTfGDPB07dsxOO+2U3r17\np3v37j/7oZ6PP/44L7/8cgYMGJC77777Jx/QaNu2bZ3PJwcAAKqPsBsAAGg2piaQrJSePXvmn//8\nZ52vXXfddTn66KN/dn+nTp2yyCKLZK655so333yTjz766P/au7/Qquv/D+Cvo791pjtuy0b+T9mU\ntSwrbWmCBIsklu3CvJAs6iLBXYRGeFEghRddhEE3ZeuPaLSSAvHC/jLTIcksWLQgHf7dLDUUV9Pp\nmrLzvfihaJvLbUfnscfj8nPen9d5fcaH3TzP+/WOPXv29Drm+II5c+ZEbW1t5Obm9rvfI0eORFVV\n1YDPUL5UWVlZbN68OR555JEeYfdAwvjB6C3svlQikYjJkyfH7bffHgUFBTFq1Kjo6uqK9vb2OHjw\nYBw+fLjP+m+++WYsXrz4qvtZvXp11NTUXPX6S/X1Tl3q9ddfj7fffrvPNYlEIkpKSmLMmDFRUFAQ\nyWQy2tvb49SpU3H8+PFoaWnp810bTNg9ceLEeOedd2LRokU9gv+cnJwoKyuLsWPHRm5ubvzxxx+x\nd+/eyyYG/FNubm5s3Ljxuu5CvuCfYfc/pVKpKC4ujsLCwigoKIicnJzo6OiIo0ePxv79+6Ojo+OK\n95aUlMQ333xzVQF+psPua+Hzzz+PuXPn/uu6EydOxOLFi/91EsHIkSOjtLQ0CgsLo7CwMM6dOxen\nTp2K9vb2aG1t7XNagLAbAABuHlc31w4AAICMeeaZZ6K7uztWrVp12W7ZSx07dqzXncRXMm/evPjw\nww8HFHRHRIwfPz4+++yzePrpp6OlpWVANSL+f/fxhg0bIpVK9fpst9xyy4BrXwvpdDoOHTrU77Hc\niUQiXn311X4F3RERL7/8cvzyyy+xc+fOft3XH6+88kqMHz8+Vq9eHX///Xeva9LpdOzbty/27dt3\nzfroy6xZs2LNmjWxYsWKy0L1c+fORVNTUzQ1NV1VnWQyGWvXrh2SoPtqnD59+qqf5VKlpaVRW1t7\n3Xeq3wiKiopi06ZN8cILL0RdXd0V1505cyZ++umn69gZAABwI3JmNwAAwBB49tlnY+PGjTFp0qRB\n1cnJyYnly5dHbW1t5OXlDapWcXFxbNmyZcBnBFdWVsbmzZsv7qDvbdT6YHvsr2txbviECRNi3bp1\nsXTp0gH1s3Hjxli5cmWfY8QH67nnnosvvvii13PCB6u8vDwjZ2M/+eSTUVNTEyNHjhzQ/WPHjo1P\nP/005s+fP+heBirT71cikYhFixbFpk2bYty4cRmtnU3y8/Njw4YN8cYbb8Rtt92W0dp5eXmxcOHC\njNYEAACGjp3dAAAAQ2Tu3Lmxbdu2WL9+fXzwwQf92smdk5MTCxYsiOXLl8e0adMy1tPo0aPj/fff\nj++//z7efffd2L59e5/jrIcPHx5z586N6urqePjhhy9eP3/+fK8jmouKijLW69UoLy+PH374Ierq\n6mLr1q2xa9euOH369IBqTZkyJRYvXhzPP//8oHbcDh8+PFasWBHV1dVRV1cXP/74Y/z666/R2toa\np0+fjo6Ojiue690fZWVlsWnTpti2bVusW7cu6uvrrzhJ4N/6vffee6OioiIWLlwYkydPHnRvF1RW\nVsaMGTNi9erV8dVXX/X5rl2Qm5sbS5YsiRdffDFuvfXWjPUyEB999FE0NDREXV1dbN++Pfbv39/r\n2dv/JplMRkVFRVRXV8esWbOuQafZacmSJVFVVRW1tbXx8ccfx8GDBwdUp7CwMB566KF47LHHorKy\ncsA/sAAAAG48zuwGAAC4AXR3d8fOnTtjx44d8fPPP0dLS0ucOHEiOjs7IycnJ1KpVEycODHKyspi\n9uzZ8eijj16XoO/kyZPR0NAQzc3Ncfz48ejq6ooRI0ZEUVFRlJaWxoMPPhijR4/ucV9zc3NUVFT0\nuL527dqoqqq65n1fSXd3d+zZsycaGxujubk5Dh06FIcPH462traLIfOIESMilUrF6NGjo7S0NKZP\nnx5z5syJ+++/f8j6zoS2trbYvn17NDY2xu7du+P333+PkydPRmdnZwwbNizy8vIilUpFUVFRFBcX\nR0lJSdx1110xZ86cGDVq1IC+80pndu/atavH2tbW1vjyyy+joaEh9u7dGydOnIizZ89GMpmMMWPG\nxJ133hnz5s2LJ554otd37kbQ1tYWjY2N0dTUFAcOHIiWlpY4evRodHR0xJkzZyKRSEQqlYr8/PyY\nMGFCTJ8+PWbMmBEVFRVRUFAw1O3f8Hbv3h07duy4+Pc9cuRInDp1Krq6uiKZTEYqlbr4v3Lq1KlR\nUlISM2fOjHvuuSeGDTPcEAAAbkbCbgAAADLuk08+iZUrV/a4/t1330VpaekQdMRQ6E/YDQAAAP3l\nZ60AAABk3NatW3tcS6VSMXXq1CHoBgAAALgZCbsBAADIqJaWlvj22297XJ89e3YMHz58CDoCAAAA\nbkbCbgAAADImnU7Ha6+9Ft3d3T0+W7BgwRB0BAAAANyshN0AAABEOp3OSJ233nqr113dhYWF8fjj\nj2fkOwAAAAAihN0AAABERENDQzz11FNRX18/oPvPnj0bL730UqxZs6bXz5cuXRp5eXmDaREAAADg\nMv831A0AAAAw9NLpdNTX10d9fX1MmjQpKisrY/78+TFjxowYOXLkFe9pbm6OLVu2xPr166Otra3X\ndcXFxVFdXX0t2wcAAAD+g4TdAAAAXObw4cNRU1MTNTU1MWzYsJgyZUqMHz8+8vPzIzc3N9rb2+Ov\nv/6KvXv3xp9//tlnrby8vHjvvfcimUxen+YBAACA/wxhNwAAAFfU3d0dBw4ciAMHDvT73oKCgtiw\nYUOUlZVdg84AAACA/zpndgMAAJBx5eXl8fXXX0d5eflQtwIAAADcpITdAAAAxN133x2rVq2KmTNn\nRiKRGHCdBx54IGpqamLz5s1xxx13ZLBDAAAAgMsZYw4AAEDk5+fHsmXLYtmyZdHW1haNjY3R2NgY\n+/fvj99++y2OHTsWHR0d0dnZGefPn49kMhkFBQUxbty4mDZtWtx3331RUVERkyZNGupHAQAAAP4j\nEul0Oj3UTQAAAAAAAABAfxhjDgAAAAAAAEDWEXYDAAAAAAAAkHWE3QAAAAAAAABkHWE3AAAAAAAA\nAFlH2A0AAAAAAABA1hF2AwAAAAAAAJB1hN0AAAAAAAAAZB1hNwAAAAAAAABZR9gNAAAAAAAAQNYR\ndgMAAAAAAACQdYTdAAAAAAAAAGQdYTcAAAAAAAAAWUfYDQAAAAAAAEDWEXYDAAAAAAAAkHWE3QAA\nAAAAAABkHWE3AAAAAAAAAFlH2A0AAAAAAABA1hF2AwAAAAAAAJB1hN0AAAAAAAAAZJ3/AddsR6mm\nBJ8NAAAAAElFTkSuQmCC\n" + }, + "figures/truncationError.png": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAABHEAAANRCAYAAABk4yD5AAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90\nbGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAW\nJQAAFiUBSVIk8AABAABJREFUeJzs3Xd4VNXWx/HfTCaTnkBI6L2IiIIURRCkS5MiIIiCdBBBOtKk\ng4heu4BSBBEVG4oiiggqKiKKDUFAEUSpCYSE9Exm3j/uay4DZ0LKyaR9P8+T596z1zlrL8gYZlbO\n2dvicrlcAgAAAAAAQIFmze8CAAAAAAAAcHU0cQAAAAAAAAoBmjgAAAAAAACFAE0cAAAAAACAQoAm\nDgAAAAAAQCFAEwcAAAAAAKAQoIkDAAAAAABQCNDEAQAAAAAAKARo4gAAAAAAABQCNHEAAAAAAAAK\nAZo4AAAAAAAAhQBNHAAAAAAAgEKAJg4AAAAAAEAhQBMHAAAAAACgEKCJAwAAcIlBgwbJYrFkfLVq\n1Sq/SwIAAJBEEwcAAAAAAKBQoIkDAMixY8eOud2x4K2vuXPn5vcfHUAu5NXPhmPHjuX3Hw0AgDxF\nEwcAABR6c+fOdfswX7Vq1fwuCQAAwHQ0cQAAAAAAAAoBW34XAAAovIKCgtSrV69sXfPFF18oOjra\nbSy7Oa677rpsnQ9kx9q1a7V27dr8LqNYiYiIUMuWLXOdJygoyIRqAAAouGjiAAByLDIyUm+//Xa2\nrmnVqpW++OILt7Hs5gBQtNStW5efAwAAZAGPUwEAAAAAABQCNHEAAAAAAAAKAZo4AAAAAAAAhQBr\n4gAAioyYmBh9++23OnLkiGJjY2W1WlW6dGndfffdCgwMzO/ysiw9PV3ff/+99u3bp6ioKPn6+ioy\nMlJ169ZVw4YNZbWa/zuYkydP6scff1RUVJSio6OVlpamkJAQlS9fXnXq1FHt2rVzNe/Jkyd18OBB\n/fnnn4qNjVVycrLCwsIUHh6umjVrqmHDhrLZiubbkvPnz+vbb7/V6dOnFRUVJZvNpsjISFWoUEFN\nmzZVQEBAns6fkJCgb775RocOHdKFCxcUHBys0qVL6+abb1aNGjXydO7CKCUlRXv27NGhQ4d07tw5\nORwOhYeHq1OnTtneuj63uZKTk7V7926dOHFCZ8+eVWpqqiIjI1WmTBndfPPNioyMzNkfMoscDod+\n+OEHHThwIGP+EiVKqHXr1qpbt26ezg0A8MAFAIAXtWzZ0iXJ7etqPvvssyuuOXr0aEZ827Ztrnbt\n2rmsVusV511+rsvlcg0cONAt3rJlyxz9WS6fZ82aNVe9pkqVKm7XzJkzJyN28eJF16xZs1yRkZGG\nfw5JroiICNe8efNcCQkJOar5UqdOnXI99NBDrjp16nic79+v8PBwV58+fVybNm1yORyOq+aOi4tz\nrV+/3tW/f39XhQoVrpo/MDDQ1bVrV9cXX3yR5fov/z5m98vT992M14fD4XC9+OKLriZNmnh8XUpy\n+fv7uzp06OD66KOPsj3H0aNHr8j32WefZcSPHDniGjRokMvf39/j/LVr13atX7/e5XQ6sz1/bmT1\ne5HX81763+yhQ4dcAwcOdAUGBhr+XV3+37eZuS736aefujp37uwKCAjw+L2zWCyum266yfX888+7\nUlNTs/13kdnPohMnTrjGjBnjKlGihOHcl54LAPAuHqcCABRaKSkpGjJkiNq3b69PP/1UTqczv0vK\nse+//15169bVggULFBUV5fG86OhozZkzRw0aNNDx48dzNFdqaqqmTJmi6tWr67HHHtNvv/121WvO\nnz+vN998U927d9cDDzyQ6bnLly9X6dKl1b9/f61fv14nTpy4av7ExER98MEHatmypbp27arY2Ngs\n/3kKml27dun666/XyJEj9e2332b6ukxOTtbWrVvVqVMntWvXTn///bcpNaxdu1Y33HCD1q5dq+Tk\nZI/nHTp0SP3799edd96plJQUU+YujJ577jndcMMNevnll5WYmJhvuU6dOqWOHTuqXbt22rJli5KS\nkjye63K59N1332nMmDGqW7fuFbv+5dTbb7+tOnXq6Pnnn9eFCxdMyQkAMA9NHABAoeRwONSzZ0+t\nWbMmv0vJtV27dqlly5bZasocPnxYt912W7abHWfOnFHr1q31n//8J9MPiJm52of9I0eOZNo4uJrN\nmzfrpptuyrSZVVBt3LhRbdu21cGDB7N97fbt29W0aVP9+uuvuarh6aef1uDBg7PVQNi0aZPuvvvu\nXM1bWC1evFhjx45VampqvuY6ePCgmjZtqq1bt2b72t9//12333673njjjWxfe6lXX31Vffr0UVxc\nXK7yAADyTtF8+BwAUOTNmzdPW7ZsyThu2rSpevbsqXr16ikiIkIxMTE6cuSINmzYkCdryJjln3/+\nUbdu3TI+cFesWFF9+/ZVixYtVK5cOTmdTv35559677339Pbbb8vlcmVc+9dff2ny5MlauXJlluaK\njY1VixYt9Pvvv18Ru+aaa3THHXeoWbNmKlOmjIKCghQTE6Pjx4/r+++/1yeffGJ43dX8u35G/fr1\ndd111ykyMlKhoaFyOp26cOGCfvvtN3322WfasmWLW3Po999/V//+/fXxxx/LYrEY5r7pppsUHx8v\nSTpw4IDbHUWBgYHq1KlTprWZvabHF198obvuuuuKO2/CwsLUt29fdejQQRUqVFBaWpqOHTumTZs2\n6b333pPD4cg498SJE2rdurX27dunsmXLZruGLVu26D//+U/GccOGDdWrVy81btxYERERio+P16+/\n/qp169bp22+/dbv2vffe06uvvqp777032/MWVp9++qlee+21jOPq1aurT58+uvXWW1WmTBmlpKTo\n77//1gcffHDVtYtykysqKkqtW7fW6dOn3cZ9fHzUrVs39ejRQ9WqVZOfn59OnDihbdu2acOGDYqJ\nick4NzU1Vf369VN4eLjat2+f7b+LAwcO6NFHH834GVO2bFn16dNHrVq1UtmyZWWxWPTPP/9o27Zt\nCgsLy3Z+AIBJ8vlxLgBAMWPWmjj/fpUoUcL13nvvZauGgrQmjsViyfj/06dPdyUlJXm89pNPPrli\njQ2bzeY6efLkVed1Op2ubt26XVFzqVKlXOvWrXOlp6dfNcdPP/3kGjZsmGvkyJGZnvfwww+7+vfv\n7/r888+ztH6Oy+VyHT9+3HXHHXdcUd/rr7+epevnzJnjdl2VKlWydJ2RnLw+YmJiXJUrV76i/s6d\nO7tOnTrl8boff/zRcE2i22+//arr1BitifPv6ykoKMj12muvebzW6XS6HnnkkSuur1u37lX/rGa4\nfN78WhPn0r+3hQsXZmttGTNzGf23ec0117i+//57j9ecOXPG8Lpy5cq5oqKirjrn5T+LLv0aM2aM\n6+LFi1muHwDgPdyJAwAotAIDA7Vjxw41aNAgv0vJMdf//9b76aef1rhx4zI9t3379nrqqac0cuTI\njDGHw6FXXnlFDz30UKbXbtiwQe+//77bWOXKlbVt2zZdc801Waq1fv36WrlypdudI0bmz5/v8e4Z\nTypVqqRNmzbprrvu0saNGzPGn3rqqULxmM+SJUuueByuc+fOeu+99+Tr6+vxuhtvvFE7duxQ8+bN\ndeTIkYzxTz75RJs2bVKPHj2yVYfL5ZKfn5+2b9+uJk2aeDzPYrFo+vTp2rdvn15//fWM8f3792vP\nnj26+eabszVvbu3fv1+9e/fOVY4xY8aoVatWObp2+fLlbv9d5UZ2c23duvWK/zarVq2qzz77TOXL\nl/d4XenSpfXOO++od+/e2rRpU8b4qVOntHDhQj399NPZrl2Spk2bpsWLF+foWgCAF+R3FwkAULyY\neSfOk08+maMaCtKdOJJcXbp0yfKc6enpV+z2dLXrnU6n64YbbrjiDp7du3dneV5vOX36tMtms7nV\n+ueff171uvy8EycxMdFVqlSpK+5wysrdEP/68ssv3e7Kysq8RnfiSHI9/vjjWZ730KFDubo+p4zq\nzu1XVv77M7quW7dupv0ZcpKrU6dOV+TZvn17lq8/f/78FTvahYSEuGJjYzO9zuhnUcOGDV1paWnZ\n/jMAALyn4C4SAABAJkqWLKlRo0bldxmmmD17dpbPtVqt6t69u9vYDz/8kOk1n332mfbt2+c2NmLE\niEzv1MgvZcqUUdOmTd3Gvvnmm3yqJmvee+89nTt3zm1s6tSpioiIyHKO5s2bX/F9/eKLL/THH39k\nq5ZSpUpp9OjRWT7/mmuu0XXXXec2drXXU1Ezc+bMfMt14sQJffzxx25jnTt3Vps2bbKco2TJklfM\ne/HiRb355pvZqkX67+vWZuNGfQAoyGjiAAAKpd69e8vf3z+/y8i1KlWqZPvRlfr167sdnzp1KtNH\nnLZt23bF2NixY7M1pzdVqlTJ7Xjv3r35VEnW7Ny50+3Yx8dHAwYMyHaeoUOHXjH25ZdfZivHHXfc\ncdUFeC93+evJrG3OC4NatWqZ9uhYTnJ99dVXbouVS9LgwYOzPXf//v1lt9vdxrL72gkKCsr243sA\nAO+j1Q4AKJQK4l0kOXHLLbdk+5oyZcpcMRYXF6fw8HDD8z///HO341q1aql27drZnjenfvzxR334\n4Yf65ZdfdODAAZ07d04XL15UQkJClq4v6FuNX36n0A033JCjnaXatm0rHx8fpaenu+XOzod6M15P\n2d223gwtW7a84nXqDWb+HMlJLqO7zNq1a5ftPKVKlVLjxo21a9euTHNnpkGDBlc0ggAABQ9NHABA\noXTttdfmdwmmKFeuXLavCQkJuWIsPj7eYxPnwIEDbsc5+aCfE2+99ZZmz56tgwcP5irPpdsoF0SX\nb73esGHDHOUJCAhQnTp19Ouvv2aMHT58OFs5zHg9/btte3Fg5s+RnOS6/LVTvXp1lShRIkfzN2zY\n0K2J88cff8jpdMpqzdqN90XlZyoAFHU8TgUAKJRy+kGnoAkNDc32NUYfypxOp+G5DodDcXFxbmOV\nK1fO9pzZkZycrO7du6tPnz65buBIBbupkJqaqsTERLexihUr5jjf5ddmt4FlxuvJ02upKDLz50hO\ncl3+/TXzteNyubJ1V1VR+ZkKAEUdd+IAAAqloKCg/C7BFNndiju7Ll9wV8rbD2sul0s9evTQ1q1b\nDeM2m03ly5dXxYoVFRwcLH9//yu24P7+++/1119/ueUsqIyaLDlppPwrLCzM7fj8+fPZuj6vX09F\njZk/R3KS6/LXj5mvHem/r5+SJUtm6fqi8jMVAIo6mjgAABQzeflBf/Xq1Vc0cPz9/TVw4EDdc889\nuummm6668O7AgQO1bt26PKvRTEYNJjP/fmnKFG2Xv37M/n7z+gGAoocmDgAAOVCQ7w65lNE6OXm5\nxsyiRYvcjkuWLKnt27erQYMGWc6RHwvr5pTR329u6r/82qzeRYHC6fLXj5mvHYnXDwAURayJAwAo\ndi7/7XROGjKFpdHg6+t7xSMax48fz5O59u3bp2PHjrmNPfroo9lq4EhSdHS0iVXlLbvdrsDAQLex\nEydO5Djf5dfyIbxou/z7a+Zrx2KxGD5iBQAo3GjiAACKneDgYLfjnCyce/r0abPKyXN169Z1O969\ne3eezPPjjz+6HVutVt19993ZypGenq6ff/7ZzLLyXK1atdyOf/jhhxzlSU5O1m+//eY2ds011+S4\nLhR8l792/vzzzxw3iPfu3et2XLNmzSzvTAUAKDz4yQ4AKHYu/+30mTNnsp0jrxoheaFVq1Zux7//\n/rsOHTpk+jxnz551O46IiMj2Qq3ffvttjppql39Y9ebjbs2aNXM73rdvX45eUzt27JDD4cg0N4qW\ny7+/LpdL27dvz3aemJiYK5o4vHYAoGiiiQMAKHYu34r3xIkT2X6E56233jKzpDx1++23XzH27LPP\nmj5Penq62/HlDYmsWLp0aY7mvvyRpqSkpBzlyYnbbrvN7djhcGj9+vXZzrN69eorxlq0aJHjulDw\nNW/e/IrHO9esWZPtPOvXr1dKSorb2OWvSwBA0UATBwBQ7DRq1OiKsffeey/L13/33Xf66KOPTKwo\nb7Vq1Ur169d3G1uxYoW+/fZbU+eJjIx0Oz5//rzbVuFXs2vXLm3YsCFHc19+d9W5c+eu+FCbV3r0\n6KGIiAi3sUcffTRb24Pv2rVL7777rttY69atVaNGDVNqRMFUvnx5de7c2W1s8+bN2rlzZ5ZzxMbG\nXrGgeGhoqO666y5TagQAFCw0cQAAxU79+vWv+ND/2GOPZelDf3R0tO65555CszvVv6ZPn+527HA4\n1KdPHx0+fDjbuTzdYdOwYcMrxp544oks5fzrr790zz33yOl0Zrse6cq1Y5xOp7755psc5couf39/\njRgxwm0sOjpagwcPztLdSGfPntWgQYOueE2NHz/ezDJRQI0bN+6KscGDB2dp3a309HQNGTLkisf3\nhg4dqpCQENNqBAAUHDRxAADFjt1u1z333OM29vvvv6t///5KTk72eN3evXvVtGlT/fHHH1c8AlHQ\n9e3bVz169HAbO378uJo1a6b169dnqXmyf/9+3X///RozZoxhvH79+qpcubLb2HPPPaenn34607zb\nt29X8+bNM+7asdlsV63lcg0bNpSvr6/b2JQpU/JsJ67LPfTQQ6pSpYrb2Pvvv69evXpdsVbQpX75\n5Re1adNGv//+u9t4x44d1bVr1zypFQVL+/btr/hv888//1SbNm30008/ebwuOjpad911lzZu3Og2\nXr58ec2cOTMPKgUAFATZf5cEAEARMHHiRK1du9Zt7ZS3335b3333nUaMGKFbbrlFJUuWVGxsrA4e\nPKjNmzdry5YtGXdLPPTQQ1qyZEl+lZ8ja9eu1U033eTWMDh37pwGDBigBQsWqFu3bmrWrJlKly6t\nwMBAxcbG6vjx4/rhhx+0bds2HThwQJI0cOBAw/wWi0UzZ87UyJEj3cYnTJig1157TQMGDNCNN96o\n4OBgnT9/XgcOHNDGjRv1+eefZ5xbp04d1atXT2+88Ua2/mwhISHq1q2b3nnnnYyx77//XtWqVVPd\nunVVqVIlBQQEuF1Tt25dzZs3L1vzeBIWFqZXXnlFrVu3dlsb6P3339fOnTvVr18/tW/fXhUqVFBa\nWpqOHTumTZs26b333lNaWppbrtKlS2vt2rWFrlGYG/v371fv3r1zneeOO+7QoEGDcl+Ql61atUp7\n9uzRyZMnM8Z+++033XTTTerevbu6d++uatWqyc/PTydPntS2bdv0+uuvX/HIntVq1bp161SqVClv\n/xEAAF5CEwcAUCzVrFlTixcvvuKRlb/++uuqv8W+8847tWjRokLXxAkLC9POnTvVo0ePK9bDOXz4\nsP7zn//keo5hw4bp/fff14cffug2/t133+m7777L9NrSpUvr/fff18KFC3M094IFC/Txxx8rISEh\nY8zpdGrfvn3at2/fFedndzHrq2nRooXefvtt9evXz+2OrgsXLmj58uVavnz5VXNUrFhRH3/8scqU\nKWNqbQVddHS0WwMupy5ftLywKFWqlHbs2KGOHTvq2LFjGeMOh0PvvPNOlv5u/Pz89Morr6ht27Z5\nWCkAIL/xOBUAoNgaN27cFQuCXs2oUaP05ptvysfHJ4+qyltly5bV559/rrFjx8put+coR3BwsMeY\n1WrVhg0brng85Gquv/567dq1SzVr1sxRTdJ/7+L58MMPValSpRznyK0ePXpo+/btqlOnTravbdeu\nnb755hvVrVs3DypDQVe7dm3t2rVLHTt2zPa1tWrV0ieffMJixgBQDNDEAQAUazNmzNDu3bvVtm1b\nWa3G/yxaLBa1bNlS27dv17Jly3K0ZktB4u/vr2eeeUa///67HnzwQVWtWvWq15QtW1b33Xeftm3b\npueeey7Tc4ODg7Vx40a98sorV21IXHPNNXrmmWf0ww8/mLITU8uWLfX777/rzTff1ODBg9WoUSOV\nLl36ikep8lKzZs20b98+rVixQk2aNPH4upL++73o0KGDPvroI23btq3Q3kkCc5QrV04fffSRPv30\nU3Xu3DnT163FYlHjxo21dOlSHThwgC3FAaCYsLgK2/YaAADkkXPnzunLL7/UyZMnFRMTI39/f1Wt\nWlVNmzZV+fLl87u8PPX777/r119/VVRUlM6dOyer1aqQkBBVqlRJderUUY0aNXK8RsuRI0e0e/du\nnT17VgkJCQoKClKlSpV044035urOm8Li3Llz2r17t86cOaOoqCjZbDZFRkaqQoUKatq0qQIDA/O7\nRBRQycnJ+uabb/TPP/8oKipKqampioyMVJkyZXTzzTerdOnS+V0iAMDLaOIAAAAAAAAUAjxOBQAA\nAAAAUAjQxAEAAAAAACgEaOIAAAAAAAAUAjRxAAAAAAAACgGaOAAAAAAAAIUATRwAAAAAAIBCgCYO\nAAAAAABAIUATBwAAAAAAoBCw5XcB+aFq1aqKi4tTtWrV8rsUAAAAAABQjBw9elShoaE6duxYtq8t\nlk2cuLg4JScn53cZAAAAAACgmMlNP6JYNnH+vQNn7969+VwJAAAAAAAoTho1apTja1kTBwAAAAAA\noBCgiQMAAAAAAFAI0MQBAAAAAAAoBGjiAAAAAAAAFAI0cQAAAAAAAAoBmjgAAAAAAACFAE0cAAAA\nAACAQoAmDgAAAAAAQCFAEwcAAAAAAKAQoIkDAAAAAABQCNDEAQAAAAAAKARo4gAAAAAAABQCNHEA\nAAAAAAAKAZo4AAAAAAAAhQBNHAAAAAAAgEKAJg4AAAAAAEAhQBMHAAAAAACgEKCJAwAAAAAAUAjQ\nxAEAAAAAACgEaOIAAAAAAAAUAjRxAAAAAAAACgGaOAAAAAAAAIUATRwAAAAAAIBCgCYOAAAAAABA\nIUATBwAAAAAAoBCgiQMAAAAAAFAI0MQBAAAAAAAoBGz5XQAAAEBB4nK5lJCQoJiYGMXHxys1NVUp\nKSlu/5ueni6bzSabzSZfX9+M/7Xb7QoLC1NYWJhCQ0Nls/FWCwAAmId3FgAAoFhISkrSP//8Y/h1\n9uxZxcTEZHylpaWZMmdQUJDCwsJUokQJlStXTuXLl8/4KleunCpUqKDq1aurTJkyslgspswJAACK\nLpo4AACgyHC5XDpx4oR+++03HTp0SIcOHdLhw4d16NAhHT9+XC6Xy6v1JCQkKCEhQSdPntSBAwc8\nnhccHKyaNWuqVq1aGV/XX3+96tatq4CAAC9WDAAACjKaOAAAoFByOp36448/9OOPP+qHH37I+N9z\n587ld2nZFh8fr59++kk//fST27jValXt2rV14403qn79+rrxxhvVuHFjlSpVKn8KBQAA+YomDgAA\nKBQSExO1Z88effXVV/ryyy/1zTff6OLFi/ldVp5yOp367bff9Ntvv+n111/PGK9du7aaNWuW8XXt\ntdfKamW/CgAAijqaOAAAoEBKSkrSzp079emnn+rLL7/U3r175XA48rusAuHfR8XWrFkjSSpRooRa\ntGih9u3bq3379qpduzZr7AAAUATRxAEAAAWCy+XS/v37tXXrVm3dulU7d+5USkpKvtTi6+ur4OBg\nBQUFyW63Z+xA9e//t1gscjqdcjgcSk9Pz/hKSUnJWAcnMTHRa2vwXLhwQR988IE++OADSVLFihUz\nGjrt27dXRESEV+oAAAB5y+Ly9gp/BUCjRo0kSXv37s3nSgAAKN7S0tL02Wef6d1339UHH3ygEydO\n5Ol8pUqVUunSpRUZGen2FR4ertDQUIWEhCgkJER+fn65vpPF6XQqMTFRCQkJunDhgs6fP6/o6OiM\n/42Ojtbp06d18uRJpaammvQnvJLVatWtt96q7t27q3v37qpZs2aezQUAAK4uNz0JmjgAAMCrEhMT\n9cknn2jjxo364IMPdOHCBVPz22w2ValSRVWqVFGlSpXcvgriTk9Op1PR0dH6559/dOLECZ04cUJH\njx7VkSNH8mSR5rp166p79+7q2bOnGjZsyGNXAAB4GU2cbKKJAwCAd6WlpWnr1q1av369PvjgAyUm\nJpqS18/PL2Nr7po1a+qaa65R1apV5evra0r+/BYTE6MjR47oyJEj+uOPP3Tw4EH9888/puWvVauW\n7rnnHt1zzz265pprTMsLAAA8o4mTTTRxAADIey6XS3v27NH69eu1YcMGRUdH5zpniRIldMMNN2R8\n1axZUzZb8VriLyYmRvv378/4OnjwoNLS0nKdt3HjxrrnnnvUt29flS9f3oRKAQCAEZo42UQTBwCA\nvHPq1CmtWbNGa9eu1e+//56rXEFBQWrUqJEaN26sG2+8URUrVuTxn8ukpqbqwIED+v7777V3714d\nOnQoVwsqW61Wde7cWcOHD1fnzp2LXZMMAIC8RhMnm2jiAABgLqfTqU8//VQvvvii3n///RxvBW6x\nWHTttdfqpptu0k033aQ6derIx8fH5GqLtri4OP3444/67rvvtHv37lytq1O+fHkNHjxYQ4cOVbVq\n1UysEgCA4osmTjbRxAEAwBxnzpzRSy+9pJUrV+ro0aM5yuHr66uGDRuqRYsWuvXWW1WiRAlziyzG\nnE6nDh48qK+//lpff/21/vrrrxzlsVgsat++vcaMGaMuXbrIarWaXCkAAMUHTZxsookDAEDu7Nu3\nT0899ZReffXVHG2P7e/vryZNmui2225TkyZNFBQUlAdV4nJ///23vvrqK+3YsUN//PFHjnLUrFlT\nDz74oAYPHqyQkBCTKwQAoOijiZNNNHEAAMg+p9OprVu36sknn9Snn36a7eutVqsaNmyo22+/Xc2b\nNy+Q230XJ8eOHdOOHTu0fft2nTx5MtvXh4SEaOjQoXrwwQdVvXr1PKgQAICiiSZONtHEAQAg61JS\nUvTKK6/oiSee0MGDB7N9fa1atdS+fXu1adNGpUqVyoMKkRsul0u//fabPv30U23btk3x8fHZut5i\nseiuu+7S9OnTdeONN+ZNkQAAFCE0cbKJJg4AAFeXlJSkVatW6bHHHtM///yTrWsDAwPVrl07de3a\nVTVr1syjCmG2lJQU7dy5U5s3b9Yvv/yS7es7d+6sGTNm6NZbb82D6gAAKBpo4mQTTRwAADy7ePGi\nXnjhBT3xxBM6c+ZMtq6tXbu2unbtqjZt2vC4VCF3/PhxbdmyRR9//LFiY2Ozde1tt92mGTNm6Pbb\nb2dLeAAALkMTJ5to4gAAcKWLFy/qmWee0VNPPaXz589n+TpfX1+1bdtWPXr0UO3atfOwQuSH1NRU\n7dixQ++88062F0O+5ZZbtHDhQrVp04ZmDgAA/48mTjbRxAEA4H+Sk5O1fPlyPfLII4qOjs7ydWFh\nYerevbu6d++u8PDwPKwQBYHL5dLPP/+sjRs36quvvlJ23kK2atVKCxcu5DErAABEEyfbaOIAACA5\nHA6tXbtW8+bNy9aaN1WqVNFdd92ldu3ayc/PLw8rREF16tQpvfPOO/rwww+VnJyc5es6deqkBQsW\nZLwXAwCgOKKJk000cQAAxZnL5dJbb72lhx9+WL///nuWr7v22mvVv39/NW3aVFarNQ8rRGFx4cIF\nbdy4URs3blRCQkKWr+vTp48WL17M1uQAgGKJJk420cQBABRXu3fv1oQJE7R79+4sX1OvXj31799f\njRs3Zl0TGEpISND777+vt956SzExMVm6xm6368EHH9TDDz+sEiVK5G2BAAAUIDRxsokmDgCguDl+\n/LimTZum119/PcvXNGrUSAMGDFD9+vXzsDIUJSkpKdq8ebNeffXVLDdzwsPDNWfOHI0aNUq+vr55\nXCEAAPmPJk420cQBABQX8fHxevTRR/XEE09kee2S66+/XsOHD1e9evXyuDoUVcnJyXr33Xe1YcMG\nxcXFZemaWrVq6cknn9Qdd9yRx9UBAJC/aOJkE00cAEBR53K59Nprr2nKlCk6depUlq6pUaOGhg0b\npiZNmvDYFEyRkJCgt99+W2+99VaW18y544479Mwzz7BeDgCgyKKJk000cQAARdmBAwc0evRoff75\n51k6v2LFiho8eLBatWrFgsXIE7GxsXr99de1ceNGpaWlXfV8Pz8/TZs2TVOnTlVAQIAXKgQAwHto\n4mQTTRwAQFEUHx+vBQsW6Mknn5TD4bjq+aGhoRo0aJC6du0qm83mhQpR3J06dUorV67UZ599lqXz\nq1WrpmeeeUZdu3bN48oAAPAemjjZRBMHAFCUuFwuvfvuuxo/frz+/vvvq55vs9l05513asCAAQoJ\nCfFChYC7AwcOaNmyZdq/f3+Wzu/atauWLl2qSpUq5XFlAADkvdz0JLhnGgCAQuzEiRPq0aOHevXq\nlaUGTvPmzbVmzRo98MADNHCQb6677jo999xzmjt3rsqWLXvV8z/44ANdd911Wrp0qZxOpxcqBACg\nYKKJAwBAIeRyubRy5Updd911ev/99696ftWqVfXkk09qwYIFqlixohcqBDJnsVjUsmVLrV27VgMH\nDrzq9uLx8fEaM2aMmjdvnuU7eAAAKGpo4gAAUMj88ccfatu2rUaMGHHV7Zv9/f11//33a+XKlWrQ\noIGXKgSyzs/PT4MGDdLatWvVrFmzq57/zTffqEGDBpo7d65SUlK8UCEAAAUHTRwAAAqJ9PR0PfHE\nE6pXr16WFoZt2bKl1q1bp759+7JwMQq88uXLa9GiRXrkkUdUvnz5TM9NS0vTvHnz1LBhQ9Y4BAAU\nKzRxAAAoBH7//Xe1aNFCkydPVlJSUqbnVqhQQUuWLNHcuXMVGRnppQoBczRt2lRr1qzRgAEDrtp8\nPHDggJo0aaK5c+dmaetyAAAKO5o4AAAUYC6XS8uWLdONN96ob775JtNzrVar7r33Xr300ku6+eab\nvVQhYD673a4hQ4ZoxYoVqlOnTqbnpqena968eWrSpIl+/fVXL1UIAED+oIkDAEAB9c8//6hjx44a\nPXq0EhMTMz23Vq1aevHFFzVs2DDZ7XYvVQjkrWrVqum5557Tgw8+KH9//0zP/fHHH9WoUSMtWbJE\n6enpXqoQAADvookDAEAB43K59Oqrr+qGG27QJ598kum5drtdI0eO1PLly1WzZk0vVQh4j4+Pj3r2\n7Km1a9eqSZMmmZ6bmpqqadOm6bbbbtOxY8e8UyAAAF5EEwcAgAIkNjZW99xzj/r3768LFy5kem69\nevW0evVq3X333fLx8fFOgUA+KVOmjBYvXqzp06crKCgo03N37dql+vXra8OGDV6qDgAA76CJAwBA\nAbF7927deOONV/3gabfbNXr0aD311FOqWLGil6oD8p/FYtHtt9+uNWvW6Kabbsr03Li4OPXr10+D\nBg3SxYsXvVQhAAB5iyYOAAD5zOl0avHixWrevPlVHwGpXbu2Vq5cqd69e8tq5Z9xFE+RkZFasmSJ\nJk2apICAgEzPffnll9WgQQPt2bPHS9UBAJB3ePcHAEA+OnnypG6//XbNmDEj08VYfXx8NGjQID3/\n/POqXLmyFysECiaLxaI77rhDq1evVv369TM998iRI7r11lu1ZMkSOZ1OL1UIAID5aOIAAJBPPvro\nI9WvX1/bt2/P9LwqVapo6dKlGjhwoGw2m5eqAwqHcuXK6cknn9T999+f6X8fDodD06ZNU9euXXXu\n3DkvVggAgHlo4gAA4GXp6emaNWuWOnfurOjo6EzP7datm1588UXVrl3bS9UBhY/ValXfvn21dOlS\nVapUKdNzt2zZogYNGmj37t1eqg4AAPPQxAEAwIvOnj2rDh06aOHChZmeFxISovnz52vChAny8/Pz\nUnVA4XbNNdfoxRdfVOfOnTM97++//1aLFi309NNPy+Vyeak6AAByjyYOAABe8vXXX6tBgwZXfXyq\nXr16WrlypVq0aOGlyoCiIyAgQFOmTNGcOXMUHBzs8TyHw6EJEyaod+/eio2N9WKFAADkHE0cAADy\nmMvl0pNPPqmWLVvq5MmTHs+zWq0aNGiQnnzySZUpU8aLFQJFT6tWrbRq1SrVrVs30/M2btyoRo0a\nad++fV6qDACAnKOJAwBAHoqPj1ffvn01adKkTHefKlWqlJ588kkNHDhQPj4+XqwQKLrKlCmjp59+\nWn369Mn0vCNHjqhp06Z66623vFQZAAA5QxMHAIA8cvToUTVr1uyqHwwbNGigFStWXHWbZADZZ7PZ\nNGrUKC1YsCDTx6sSEhLUp08fTZs2LdOGKwAA+YkmDgAAeWD79u1q3LjxVR/R6N+/vx5//HGFh4d7\nqTKgeGrevLlWrFiha665JtPzlixZos6dO+v8+fNeqgwAgKyjiQMAgIlcLpeeeeYZdejQIdMPgSEh\nIXrkkUc0dOhQHp8CvKRcuXJ67rnn1KNHj0zP++STT9S4cWP9/PPP3ikMAIAsookDAIBJkpOTNXjw\nYI0fPz7TxzFq166tFStWqGnTpl6sDoAk2e12jRs3TjNmzJDdbvd43tGjR9W0aVNt3LjRi9UBAJA5\nmjgAAJjg5MmTatmypV5++eVMz+vQoYOeffZZlS1b1kuVATDSvn17Pffcc5nuBJeUlKRevXpp8eLF\ncrlcXqwOAABjNHEAAMilvXv3qnHjxtqzZ4/Hc6xWq0aPHq2pU6dm+tt/AN5zzTXX6MUXX1SDBg0y\nPW/GjBkaNGiQUlJSvFQZAADGaOIAAJALmzZt0m233aZTp055PCc0NFSPPfaYevfuLYvF4sXqAFxN\nWFiYHn/88atuQ75u3Tq1a9dOUVFRXqoMAIAr0cQBACAHXC6XnnrqKd15551KTEz0eF716tW1fPly\nNWrUyIvVAcgOHx8fjRo1Sg8//HCmd8p99dVXatKkifbv3+/F6gAA+B+aOAAAZJPD4dDo0aM1ceLE\nTNfJaNmypZ5//nmVL1/ei9UByKm2bdvqmWeeUalSpTyec/ToUTVr1kwff/yxFysDAOC/aOIAAJAN\ncXFx6tq1q5YvX57peUOGDNGcOXMUEBDgpcoAmOHaa6/V8uXLVbNmTY/nxMXFqUuXLnrhhRe8WBkA\nADRxAADIsuPHj6t58+aZ/gbebrdrzpw5GjBgAOvfAIVUZGSknn32WTVv3tzjOU6nU6NGjdLMmTPZ\nuQoA4DU0cQAAyIIff/xRTZo00b59+zyeU7JkST311FNq1aqV9woDkCcCAgI0b9483XPPPZme98gj\nj2jQoEFKTU31UmUAgOKMJg4AAFexY8cOtWzZUqdPn/Z4TpUqVbR06VJdd911XqwMQF6yWq0aPny4\npk6dKpvN5vG8devW6Y477lBcXJwXqwMAFEc0cQAAyMQbb7yhjh076uLFix7PadSokZ5//nmVK1fO\ni5UB8JaOHTvqiSeeUGhoqMdztm3bppYtW+rkyZNerAwAUNzQxAEAwINnn31W/fr1U1pamsdzunTp\nokcffVTBwcFerAyAt9WrV++qzdqffvpJTZs21W+//ebFygAAxQlNHAAALuNyuTR9+nSNGzcu0wVL\nR44cqUmTJmX6mAWAoqNSpUp6/vnnVbt2bY/nHD9+XLfeequ++uorL1YGACguaOIAAHCJtLQ0DRky\nRI8++qjHc2w2m2bNmqW7776bHaiAYiY8PFxPPfWUmjRp4vGcmJgY3X777froo4+8WBkAoDigiQMA\nwP9LSEhQjx49tHbtWo/nBAQE6NFHH1WbNm28VxiAAiUgIEALFy5Up06dPJ6TlJSkbt266Y033vBi\nZQCAoo4mDgAAkmJjY9WhQwdt2bLF4zklS5bU008/rUaNGnmxMgAFkc1m05QpUzRo0CCP5zgcDvXr\n108rVqzwXmEAgCKNJg4AoNiLjo5WmzZt9PXXX3s8p3z58nruued0zTXXeLEyAAWZxWLRwIEDNXny\nZFmtxm+rXS6XRo4cqSVLlni5OgBAUUQTBwBQrJ08eVItW7bUDz/84PGcWrVq6bnnnlOFChW8WBmA\nwqJLly5auHCh7Ha7x3OmTZumqVOnZrpYOgAAV0MTBwBQbB07dkwtWrTQgQMHPJ7TqFEjPf300woP\nD/diZQAKm6ZNm2rJkiUKDAz0eM5jjz2m+++/X+np6V6sDABQlNDEAQAUSwcPHlTz5s31559/ejyn\nZcuWWrx4caYfygDgXzfeeKOefPJJhYaGejxnxYoVuvfee5WWlubFygAARQVNHABAsfPTTz/ptttu\n04kTJzye06lTJ82aNUu+vr5erAxAYVe7dm09++yzioiI8HjOG2+8ob59+yo1NdWLlQEAigKaOACA\nYmX37t1q3bq1oqKiPJ7Ts2dPTZ48WT4+Pl6sDEBRUaVKlauuo/Xuu++qd+/eSklJ8WJlAIDCjiYO\nAKDY+Prrr9W+fXtduHDB4zn9+/fXmDFjPO40AwBZUbZsWT377LOqUaOGx3M++OAD9ejRQ0lJSV6s\nDABQmPEOFQBQLHz55Zfq0KGD4uPjPZ4zYsQIDR06VBaLxYuVASiqwsPD9fTTT6tu3boez/n444/V\nrVs3JSYmerEyAEBhRRMHAFDk7dy5U506dVJCQoLHc8aNG6d+/fp5sSoAxUFwcLAef/xx1a9f3+M5\nn376qbp06ZJpkxkAAIkmDgCgiPviiy8ybeBYrVZNmzZNPXr08G5hAIqNgIAAPfroo2rUqJHHcz7/\n/HN16tRJFy9e9GJlAIDChiYOAKDI+vzzz9W5c2ePjylYrVbNmjVLHTp08HJlAIobf39/LVq0SDff\nfLPHc7766ivdfvvtio2N9WJlAIDChCYOAKBI2rFjR6YNHB8fH82ePVutWrXybmEAii0/Pz8tWLBA\nTZs29XjO7t271blzZ+7IAQAYookDAChytm/frjvuuMPjji//NnBatmzp5coAFHd2u13z5s1TixYt\nPJ6za9cudenSJdN1vAAAxRNNHABAkfL5559ftYEzZ84c3XbbbV6uDAD+y9fX96qN5C+//FJdu3Zl\n1yoAgBuaOACAImPXrl264447lJycbBi32WyaO3dupr8BBwBvsNlsmjVrltq2bevxnM8++0w9evTw\n+DMNAFD80MQBABQJe/fuzXQXqn8bOM2bN/dyZQBgzMfHR9OnT1ebNm08nrNt2zb16tVLKSkpXqwM\nAFBQ0cQBABR6v/zyi26//XbFxcUZxn19fTV//nzdeuutXq4MADL3byMns0c8t2zZoj59+ig1NdWL\nlQEACiKaOACAQu3gwYNq3769zp8/bxj38fHRvHnzMt0NBgDyk81m08MPP6xmzZp5POf9999Xv379\nlJaW5sXKAAAFDU0cAEChdeTIEbVt21Znz541jFutVs2aNYsGDoACz9fXV3PmzFGTJk08nrNx40YN\nGjRITqfTi5UBAAoSmjgAgELp+PHjatOmjU6ePGkYt1gsmj59OtuIAyg07Ha75s+fr8aNG3s857XX\nXtOYMWPkcrm8WBkAoKCgiQMAKHROnTqlNm3a6Pjx4x7PmTx5stq1a+fFqgAg9+x2uxYsWKAGDRp4\nPGf58uWaOXOmF6sCABQUNHEAAIVKTEyMOnTooCNHjng8Z+zYsercubMXqwIA8/j7+2vRokWqV6+e\nx3MWL16sJUuWeLEqAEBBYMvvAgAAyKqEhATdcccd2rdvn9t4zUv+f7+771aXm26S/vnnqvmcNptS\nypY1jPmdOSNrDhcQTapQQbJYrhj3jYmRzcMW6FeTUrq0nHb7FeM+8fGyX7iQo5xpJUrIERx8xbgl\nNVX+HtYZuhpHYKDSwsMNYwFZ+J4Y4fvE96k4fp8CJD3x0EN6cOFCHTx48Ip4JUnTpk1TiRIlNHLk\nyBxUDAAojGjiAAAKhdTUVPXu3Vu7du26InZQks+/Bxs2/PcrC+Jr1ND3q1YZxurOnatQgw9OWfH5\np59KPj5XjFddu1YV3n8/Rzn3Llumi3XqXDEe+cUXuvY//8lRzsPjx+tk9+5XjAcdP67Gw4fnKOep\nTp106KGHDGM3DxwoSw4WZOX7xPepOH+flixZovHjx+vo0aNusaOSfpLU8f77FRoaqn79+uVoDgBA\n4UITBwBQ4KWnp2vgwIH6+OOPTc3rcElRKcYfVh3OnC8aGpXilHyuvHOgUnrOc8akuRRjUGuQI+c5\nLzpchn/+1NSc73yTnG6cMzf4PvF9Ks7fpxS/YE1buESzJ4/TmVOn3OKNJD0u6b777lNoaKi6dOmS\n47kAAIUDTRwAQIHmcrk0duxYbcj07hqLpBx8+PKxyVaqjHHM5pv9fP9eWqqM4Z0DFv+AnOcMCzes\n1Sc4NMc5fYJCDHPaomNynNPiH+D57zSn+D7xfSrm36fIUmU0d/kazRx+n2Kjzir9knMGSXrO4VDv\n3r318ccfsyMfABRxNHEAAAXanDlztGzZMvlIbh9c/tW2SzelHPhVlhz8pt9ZubJKe1gXxFmpspJy\nuN5G6fBwww+dvuXKK6lKtRzlDIuIkK9BrYFlyuY4Z0DZsoZ//oCIiBzntJWv4PHvNLlKVYnvU7bx\nfeL7JP337+GZV97UuLt7aO6FC7r0b+QJSa2Tk9WtWzft3LlT9evXz9F8AICCz+JyuXJ+32gh1ahR\nI0nS3r1787kSAEBmnnnmGY0fP16S9KGks5JmSjr5//FbW7fV8+vfkN1ggVIAKIp+/ekHvdq1kzYl\nJ7mN3ynpPUlly5bVN998o6pVq+ZDdQCArMhNT4ItxgEABdL69eszGjgdJXXWfx8bOCxptqQGDRvr\n6TXraeAAKFauv7Ghem54R1ut7m/jH5fkK+n06dPq0KGDoqOj86U+AEDeookDAChwtm3bpsGDB0v6\n765TT1wSC5LUKSBQz7/+lgKDgvKjPADIVzfd2lwXHv2PHJeM1ZQ05v///+HDh9WlSxcl5PARNgBA\nwUUTBwBQoPz444/q2bOnHI7/fjwZLum6S+JOST5rXlGJ8FL5UR4AFAg3DB6mX1q4L2I8W9K/Pxn3\n7NmjPn36KC0tzeu1AQDyDk0cAECBcezYMXXu3Fnx8fGSpDBJ8y87569OXRTUtr3XawOAgiZoxRol\n+fllHJeQNOeS+JYtWzR8+HAVwyUwAaDIookDACgQzp07p44dO+r06dMZYzMkRV5yTpqfn9Iee9Lr\ntQFAQZQeEaG4aQ+7jY2SVPuS45dfflkzZ870al0AgLxDEwcAkO+SkpLUtWtXHTp0KGOsmqRxl50X\nNWa8HGXLebU2ACjIzg+/X6mVq2Qc2/TfRY4vtXjxYj333HNerQsAkDdo4gAA8lV6erruueceffPN\nN27jSyT5XXKcXKasYsdO8GptAFDQufz8dGbOArexrpLaXnbeuHHj9O6773qtLgBA3qCJAwDINy6X\nS2PHjtV7773nNn6rpLsuO/fszDlyBQZ6qzQAKDQudu2uxCZN3caelPsbfZfLpXvvvVfffvutV2sD\nAJiLJg4AIN88+uijWrZsmduYRdJTl5138Yb6iu/bz2t1AUChYrHo9IJH3IZi9L+dqv7176Orf/75\np9dKAwCYiyYOACBfvPHGG5oxY8YV4/dIuumysaiFiyUr/2QBgCfJDRrpwl19lVylqj6eNlvdwkoo\nyuC8qKgode7cWefPn/d6jQCA3OMdMQDA63bt2qWBAwdeMR4gafFlY+c6dlFys+ZeqQsACrPTjzym\no19/Jw0YpBlPPCe7n5/heYcOHVLPnj2VkpLi5QoBALlFEwcA4FVHjhxR9+7dDT88DJNU6ZJjp69d\n5+Yt9FptAFCYOUuUlMvPT6VDQ1SncRONnjFHFovF8NwvvvhCQ4cOlcvl8nKVAIDcoIkDAPCamJgY\ndenSRdHR0Ybxt0qV0p5Bg5USGiZJOjtkuBzVa3izRAAo9Pz9/RTo76fmnbrqvpEPeDzv1Vdf1Zw5\nc7xYGQAgt2z5XQAAoHhITU1Vr169dOjQIcO4v7+/Fjz6qP6qXENn7h2qum+/rtQpU71cJQAUDaXD\nQpSUkqpOffvr/OmT2vLeu0o3OG/BggWqVq2aBg8e7PUaAQDZx504AIA853K5dP/99+uzzz4zjFut\nVs2ePVvlq1aT0+4vlS6ji3PmyxlWwruFAkARYbPZFBYYoJA0h55ITdPekBCP544YMULbt2/3YnUA\ngJyiiQMAyHOLFy/WmjVrPMYfeOABNbnlFl10+sgeHKaQAD/5+vp6sUIAKGJcLl2zbrXa9+ykWls2\nq/7Fi5pQrpzhqQ6HQ3fddZcOHz7s5SIBANlFEwcAkKfeeOMNzZw502P8zjvvVK9evRSfli6Lf6B8\n/fwUEer5N8YAgCywWBT4/R75xsdnDC1IS1OV0qUNT4+JiVHXrl0VExPjrQoBADlAEwcAkGf27Nlj\nuJX4v5rffLMeLVtWrsREJVh8ZQ8JU8mgQFl9fLxYJQAUTWfnzJfL9r8lMIOio/XObbcpKCjI8PzD\nhw/rrrvuUlpamrdKBABkE00cAECe+OeffzxuJS5JNWrU0Iv16+ua5ct1y8CBqvHlTvnZbCoRHOjl\nSgGgaEqtUUvnh45wG6u/ZYv+M2WKfDw0y7dv367x48d7oToAQE7QxAEAmC4xMVE9evTQ6dOnDeMR\nERH6z8yZqrVhgyQpIDpaNy+YrRvWrZLFyj9NAGCWqEkPKb1EiYxjW2Kiun3/vcaOHevxmmXLlmnp\n0qVeqA4AkF28UwYAmMrlcmnIkCHau3evYdzf31+LFi1S482b5XvxYsa4IyhYCYOHeatMACgWnCXD\nFTV5mttYuS1b1O/669WrVy+P140bN06ffPJJXpcHAMgmmjgAAFMtWrRIb7zxhsf4zJkzVd/fX+U3\nbXIbPzNuotI9LLgJAMi580OGK6VGzYxji9OpGsuWadT99+vmm282vCY9PV19+vTRwYMHvVUmACAL\naOIAAEyzceNGzZo1y2N86NChat68uWq8+KKs6ekZ40kVKilu1BhvlAgAxY+vr87MXeg2FL53ryK/\n/16zZs1SlSpVDC+LjY3VHXfcoXPnznmjSgBAFtDEAQCY4qefftKAAQM8xtu0aaN7771XJX74QRG7\ndrnFzs6eJ5e/f16XCADFVnyHTkpo0dJtrMby5Qr5/0dcQ0NDDa87cuSI+vTpI4fD4Y0yAQBXQRMH\nAJBrZ8+eVffu3ZWYmGgYv/baa/XQQw/J4nSq5rJlbrG4Bo2UcKfndRkAACawWHR63iK5LJaMoaDj\nx1Xugw9UoUIFzZ8/X7ZLtiO/1I4dOzRlyhRvVQoAyARNHABArqSkpKhnz546fvy4YTwiIkILFiyQ\nn5+fyn78sYKPHHGLRy9aIl3yoQIAkDdSbqinC/36u41VXbtWtvh41a9fP9OtxZ9++mmtW7cujysE\nAFwNTRwAQK48+OCD+vrrrw1jdrtdCxYsUEREhHwSE1XtpZfc4tHdeyr5JuNFNQEA5ouaPkvOwKCM\nY3tcnCps3ChJ6tKli/r06ePx2hEjRuj777/P8xoBAJ7RxAEA5NiKFSu0cuVKj/GpU6fq2muvlSRV\nfv11+Z0/nxFL9/PT+bkL8rxGAMD/OMqWVfTYCZKktOBg/TjyAR3ufVdGfMSIEWrcuLHhtSkpKbrz\nzjt15swZr9QKALgSTRwAQI588803GjPG845SAwYMUJs2bSRJfmfOqOKbb7rFz454QI6KlfK0RgDA\nlc6NGqPosRP1zSc7dWzoKMXa/OV0uSRJPj4+mj17tsqXL2947T///KPevXsrNTXVmyUDAP4fTRwA\nQLadPHlSvXr1UlpammG8efPmGjRoUMZx9ZUr5XPJG/6UyEjFTpyc12UCAAy4AgN1dtZclahWVTb/\nALn8ApTocGbEQ0JCtHDhQvl72DXwq6++0rhx47xVLgDgEjRxAADZkpqaqt69e+vUqVOG8SpVqmj6\n9OmyWv//nxinU6nh4XL6+GScc3baw3IGh3ijXACABzabTWEB/vILCVO8bBl340hStWrVNH36dI/X\nvvDCC1qxYoU3ygQAXIImDgAgW8aNG6dvvvnGMBYUFKSFCxcqMDDwf4NWq34fNUpbVq7VyVZtFX/t\ndbp4731eqhYAkJnw0GD52v3kExCki2lOt9htt92mAQMGeLx2zJgx2rVrV16XCAC4BE0cAECWrVq1\nSi+88IJhzGKxaObMmapYseIVsYtpTiXVrK0fnn1Rxz/cKl1yVw4AIP9YrVaFBwfKNyhEKQ6Xyr39\ntqxJSRnxQYMGqVmzZobXpqWlqVevXjpx4oS3ygWAYo8mDgAgS7799luNHj3aY3zQoEFq2rTpFePp\nTpeSLL7yDQ5VeHCgFBqWl2UCALIpNMBfVT7fri7DB6n20qWqdMlC9FarVTNmzFDlypUNrz19+rR6\n9uyplJQUb5ULAMUaTRwAwFWdPn1avXr18rgbya233qr+/fsbxmIdTvkGhcjPbldYUKDhOQCA/BO+\ndrUaTBytoJP/vaOm0oYNskdFZcSDgoK0YMECBQUFGV6/Z88ejR8/3hulAkCxRxMHAJCp1NRU3XXX\nXR5vl69UqZL7QsaSrMnJ/13Q2JGuFB8/2YKCFREaLIuVf3YAoKCJvauvHBERGce25GRVX73a7ZzK\nlStr5syZslgshjleeOEFrVu3Lk/rBADQxAEAXMWkSZP01VdfGcYCAwO1cOHCK347W2P5cjUcPVq2\nffvlFxyqQD+7ggKMt6oFAOQvZ2iYoqbOdBsru3Wrgg8dchtr2rSphgwZ4jHPyJEj9fPPP+dJjQCA\n/6KJAwDw6LXXXtPzzz/vMT59+vQr1kkIOnpU5TdvVujBg2ozcZyazJ6uMulpeV0qACAXYvoPVPK1\nddzGaixfLl2y7bgk3XvvvWrRooVhjuTkZPXq1UsXLlzIqzIBoNijiQMAMHTgwAENHz7cY/y+++5T\n8+bNrxivsXy5LM7/bVNb8tAB2UqWzJMaAQAmsdl0Zt4it6GSP/+siMvuxLRYLJo6daoqVapkmObI\nkSMaOHCgnE6nYRwAkDs0cQAAV7h48aJ69eqlxMREw3jTpk01cODAK8bD9+xR+HffuY1FzV0o2e15\nUicAwDwJbdopvk07t7HqL7wgS5r73ZRBQUGaN2+e/P2NH5N9//33tWTJkjyrEwCKM5o4AAA3LpdL\nw4cP18GDBw3j5cuX14wZM9wWMpYkS3q6aixb5jZ2oUkzJXTpmme1AgDMdWbeIrl8fDKOA0+eVIV3\n373ivGrVqmnSpEke8zz88MPavn17ntQIAMUZTRwAgJulS5fqjTfeMIzZ7XbNmzdPwcHBV8TKbd6s\noL/+yjh2WSw6t2ix5GEnEwBAwZNybR3F3DfIbazKunXyjY294tx27drpzjvvNMzjdDrVr18//fPP\nP3lRJgAUWzRxAAAZdu/erYkTJ3qMjx8/XjVr1rxi3BYfr6pr1riNRfXuq5T6DUyvEQCQt6Iemqn0\nkNCMY9+EBFV5+WXDc0eNGqW6desa54mK0l133aXU1NQ8qRMAiiOaOAAASVJ0dLT69OmjtDTjnaQ6\ndeqkTp06GcYqr18v+yW/pXUEBOjC7Hl5UicAIG+lR0QoeuIUt7HymzYp8PjxK8719fXVnDlzVKJE\nCcNcu3fvzvSxKwBA9tDEAQAoPT1d9957r/7++2/DeM2aNTVu3DjDmP/Jk6q4caPb2NkHxspRtpzp\ndQIAvOP88PuVWqVqxrHV6VT15csNz42MjNSsWbOuWCvtX88//7xee+21vCgTAIodmjgAAC1cuFCf\nfPKJYSwoKEhz586Vn5+fYbz6ihWyXnL3TnKZsoodOyFP6gQAeIfLz09nZs/POHZarYqPiJDF4TA8\nv2HDhho6dKjHfCNHjtShQ4dMrxMAihuaOABQzG3dulXz5nl+9GnatGmqUKGCYSxs3z6V/uILt7Gz\nM+fIFRhoao0AAO+72LW7Eps01fkWrfTZhve0e+xkpV+yc9Xl+vXrp1tvvdUwFh8frz59+igpKSmv\nygWAYoEmDgAUY3///bfuvfdeuVwuw3jfvn3VvHlz44udziu2FL94Q33F9+1ndpkAgPxgsej4hrd1\n6u33lFKnrmyBwYpLc2ZyuiXTxv8vv/yi8ePH51GxAFA80MQBgGLK4XCoX79+OnfunGG8Xr16Gj58\nuMfrS/z0k0IPHnQbi1q4WPKwJgIAoPBxBofIYrUqPCRIvkEhSrL6yuH03MgJDg7W3Llz5evraxhf\nsWIF6+MAQC7wThsAiqk5c+bo66+/NoyVLFlSs2fPlk8mt81faNhQex//j2Kq/3fL8XMduyi5mYe7\ndgAAhVpoUKD87L7yCw5VrPGyOBlq1qypBx980GOc9XEAIOdo4gBAMfTJJ59o8eLFhjGr1arZs2er\nVKlSV83zV70G2vHyBu2b/6jOzVtodpkAgAKkdGiIbAFBSrX5KTnNIWtyssdz77jjDrVp08Ywxvo4\nAJBzNHEAoJg5deqUBgwY4HEdnCFDhujGG2+8ap7UdKdSfOzyDQ5VyuChclSvYXKlAICCxN/fT0H+\nfirzzz9qOGmSaj/+uMdzLRaLJk2apIoVKxrGf/nlF02YwE6GAJBdNHEAoBhJT09X//79dfbsWcN4\n48aN1a9f1hYmjk23yC8kTIEBfgr0N95+HABQdFjjL6rBrKlqM/Buld73i8rs2KHQAwc8nh8YGKg5\nc+Z4XB/nxRdf1Ouvv55X5QJAkUQTBwCKkcWLF2vHjh2GsfDwcM2YMUPWLCxMnJCWLqfdX77+AYoM\nDTa7TABAAeQMCFTAb+5NmxpLl0oe7uyU/rs+zpgxYzzGR4wYocOHD5tWIwAUdTRxAKCY2Llzp+bM\nmWMYs1gsmjlzpkqWLOk5gculKq+8IvupU4p3+cgeHKaQAH+Pv2EFABQxPj46s+ARt6GwAwcU+dln\nmV7WtWtX1scBAJPQxAGAYiAqKkr9+vWT08O2sAMGDFDDhg0zzVHq669V7aWX1GTgQNVbt0YBaamK\n4C4cAChWEpvfprhOXdzGqq9YIWtqqsdrLBaLJk6cqAoVKhjGf/75Z40fP97MMgGgyKKJAwBFnNPp\n1MCBA3Xy5EnDeP369XXfffdlmsOSlqYaL74oSfJJS1OdV9ep0aI5smayBTkAoGg6O2e+XDZbxnHA\nmTOq+PbbmV4TFBSU6fo4K1as0NtXyQEAoIkDAEXek08+qY8++sgwFhYWppkzZ8rnKs2YCps2KfCf\nfzKOXVarYqdMM7VOAEDhkFqjls4PHeE2VvnVV+V7/nym19WqVSvT9XGGDx+u48ePm1IjABRVNHEA\noAjbvXu3pk+f7jE+ffp0RUZGZprDFhenKuvWuY1F9euv1LrXm1IjAKDwiZr0kNJLlMg4tiUmqtqa\nNVe9rmvXrmrdurVh7MKFC7r33nvlcDjMKhMAihyaOABQRMXGxqpfv34e3wz37dtXTZo0uWqeqi+/\nLN+LFzOOHUHBipkx27Q6AQCFj7NkuKImu9+RWW7LFgX9+Wem11ksFk2aNEnly5c3jH/11VdauHCh\naXUCQFFDEwcAiiCXy6VRo0bp2LFjhvHrrrtOw4YNu2qegOPHVX7TJrexM+MmKr10aTPKBAAUYueH\nDFdKjZoZxxanUzWWLct0y3Hpv+vjPPzwwx4f5V2wYIG+/PJLU2sFgKKCJg4AFEHr16/X66+/bhgL\nDg7WrFmzZLtkUUpParz4oqzp6RnHSRUqKW6U5/UMAADFiK+vzsx1v2smfO9ehX/77VUvrVOnjoYO\nHWoYczqduvfeexUTE2NKmQBQlNDEAYAi5siRIxo9erTH+JQpU1S2bNmr5inxww+K2LXLbezs7Hly\n+fvnukYAQNEQ36GTEprf5jZWY/lyWbKwrk3fvn3VqFEjw9jff/+t4cOHy3WVu3oAoLihiQMARUha\nWpruvfdeXbxkDZtLdevWTbfddpthzE16umouW+Y2FNuwsRLu7GVGmQCAosJi0en5j8hlsWQMBR0/\nrlLffHPVS61Wq6ZPn66wsDDD+DvvvKNVq1aZVioAFAU0cQCgCJk3b56+9XAbe5UqVTRq1Kgs5Sn7\n8ccKPnLEbezcwkelS96kAwAgSSk31NOFfv0lSRerVdfnC5foVNNmWbq2VKlSmjp1qsf4uHHjdODA\nAVPqBICigCYOABQRX3zxhR555BHDmK+vrx5++GH5Z+FRKJ/ERFV76SW3sejuPZV8082m1AkAKHqi\nps/SqSVP6Jv3Ptb5th0Um571pn/Tpk3Vs2dPw1hSUpL69eun5ORks0oFgEKNJg4AFAExMTHq37+/\nx7UDRowYoZo1axrGLlf59dfld/58xnG6n5/Oz11gSp0AgKLJUbasYoYMV2SpcNkCAuXw9VOSI/3q\nF/6/kSNHqkaNGoaxX375RQ899JBZpQJAoUYTBwAKOZfLpREjRuiff/4xjN98880ef8NpJLFCBaWU\nLJlxfHbEA3JUrJTrOgEARZ+fn11B/n7yCwnTRadVziwuTGy32zVr1iz5+fkZxp977jlt3rzZzFIB\noFCiiQMAhdxLL72kt99+2zBWokQJTZ06VVZr1n/cn+nYUR++9IoODhqmpAoVFTtxslmlAgCKgciw\nENn8A+TyC1Ciw5nl66pUqaIxY8Z4jA8dOlRnz541o0QAKLRo4gBAIXbo0CGNHTvWY3zq1KkKDw/P\nVs6EtHSllQjX7xOm6vdd38sZHJLbMgEAxYjNZlNYgL/8QsLkOHdBVdaskZxZa+Z06dLF4y6KZ8+e\n1bBhw9h2HECxRhMHAAqp1NRU3XPPPUpMTDSM9+zZU7fccku2cjpdLl10+cgvpIRCA/1lCww0o1QA\nQDFTyseiOqtX6I7B/VVt3TqV2bYtS9dZLBZNnjxZpUuXNox/8MEHWrlypZmlAkChQhMHAAqpuXPn\n6ocffjCMVa9eXSNHjsx2zotpTvkEBMlmt6tUKHfgAABypty8Waq97GnZ/n9XqWqrVsmalJSla0NC\nQjRjxgxZLMY7XE2YMEGHDx82rVYAKExo4gBAIfTVV19pyZIlhjG73a6HH35Ydrs9S7ksqanySUxU\nutOlJIuvfINDFR4cmK11dAAAuNS5MePkvOTfIf/oaFV6880sX1+/fn3dfffdhrHExEQNGDBAaWlp\nua4TAAob3qEDQCFz8eJF3XfffXJ6WF9g1KhRqlatWpbzVXznHTXp318lP9gsX/9A+dntCgviMSoA\nQM6lVa2m8yMfcBurtGGD7FFRWc4xePBg1axZ0zC2Z88eLVy4MFc1AkBhRBMHAAqZCRMm6OjRo4ax\npk2bqnv37lnO5RsToyrr18seE6OGTz+pdsP6q+LpE7JwFw4AIJeix0+SIyIi49iWnKzqq1dn+Xpf\nX1/NnDnT452lixYt0jfffJPrOgGgMOFdOgAUIps2bdJqD2+Aw8LCNHnyZI9rCBipunatbJcsjBx4\n5rTslSrmuk4AAJyhYYqaOtNtrOzWrQo+dCjLOapWrepxjbf09HQNGDBA8fHxuaoTAAoTmjgAUEic\nOXNGw4cP9xifPHlytrYTDzp6VOU3b3afY+JDSg8vleMaAQC4VEz/gUq+to7bWI3ly6VsbBPeo0cP\nNW7c2DB25MgRTZgwIVc1AkBhQhMHAAoBl8ulYcOGKcrDWgKdOnVS8+bNs5WzxvLlslyyrk5ilaqK\nG5b9Ha0AAPDIZtOZeYvchkr+/LMivvoqyymsVqumTp2q0NBQw/iqVav03nvv5aZKACg0aOIAQCGw\natUqbb7srpl/lStXTmPGjMlWvvA9exT+3XduY1FzF0pZ3NEKAICsSmjTTvFt2rmNVX/hBVmysbtU\nRESEJk2a5DE+fPhwnT59Osc1AkBhQRMHAAq4P/74w+Ot4larVdOnT1dgYNZ3k7Kkp6vGsmVuYxea\nNFNCl665qhMAAE9Oz39ELh+fjOPAkydV4d13s5XjtttuU8eOHQ1j0dHRGjJkiFzZeEwLAAojmjgA\nUIA5HA7dd999SkhIMIzffffduuGGG7KVs9zmzQr666+MY5fFonMLH5GysSAyAADZkVr7WsXcN8ht\nrMq6dfKNjc1WnjFjxqhcuXKGsY8++kirVq3KaYkAUCjQxAGAAmzJkiUet0+tWbOmBg0alK18PvHx\nqrpmjdtYdK8+SrmxYU5LBAAgS6Iemqn0kP+ta+ObkKAqL7+crRxBQUGaPn26rFbjjzETJ07U0aNH\nc1UnABRkNHEAoIDau3ev5s6daxjz9fXVjBkz5Ovrm62cVdavl/2S33o6AgIUM2d+bsoEACBL0iMi\nFD1xSsZxSmioYitWzHaeG264Qffcc49hLD4+XoMHD5bzkoX7AaAooYkDAAVQcnKy7rvvPjkcDsP4\niBEjVK1atWzl9D95UhU3bnQbO/vAWDnKGt+WDgCA2c4Pv18pNWvp+KBh2rbxI/16x51y5mAdm4ED\nB6pWrVqGsS+++ELPPvtsbksFgAKJJg4AFECzZ8/WgQMHDGMNGjRQz549s52z+ooVsl6yE0hymbKK\nHWu8YDIAAHnB5eenI198owuPPi5X6TKy+AUqwZH9u2ZsNpumT5/u8Y7U6dOn6+DBg7ktFwAKHJo4\nAFDA7Nq1S//5z38MY0FBQZo2bZrHtQA88Tt7VhG7drmNnZ05R65s7GoFAIAp7HbZfHxUIjBA9pAw\nJciWo7txqlWrpsGDBxvGkpOTNXDgQI93tAJAYUUTBwAKkMTERA0aNMjjFqnjxo1T6dKls503pXRp\n7X75Zf3VsrUk6eIN9RXft1+uagUAIDfCQ4Jkt9tlCwxWXFrO1rDp06eP6tataxjbs2ePlixZkpsS\nAaDAoYkDAAXI9OnT9fvvvxvGWrRooXbt2uU4d1Sp0tqz8DF9/cpbOvOfp6Vs3s0DAICZLFarwkOC\n5BsUoiSrr5yJibImJWUrh4+Pj6ZNmyY/Pz/D+Lx58/TTTz+ZUC0AFAy8gweAAiKzhRjDwsI0YcIE\nWSyWHOV2pDuVaPGVb1CIrM2bK7Vho9yUCgCAKUKDAuVn81HNr7/SLQMHqcr69dnOUbFiRY0cOdIw\nlpaWpoEDByolJSW3pQJAgUATBwAKgH+3RPVkwoQJKlmyZI7zx6VL9uBQ+dvtCg0MyHEeAADM5Hvs\nqFr0v0s3zZ2pwOgoVXzrLfmdPp3tPN27d1fDhg0NY7/88ovmz5+f21IBoECgiQMABcCUKVN09OhR\nw1ibNm3UsmXLHOdOTXcqxcdPvgFBiggLkYXHqAAABYQjIlL206cyjn3S0lR95cps57FarXrooYcU\n6GHB/kcffVS7d+/OcZ0AUFDwTh4A8tm2bdv0wgsvGMbCw8M1duzYHOWtvH69Svzwg2LTLfILCVWA\nv12B/sZrBgAAkB9cwcE6O2O221iZHTsUeuBAtnOVKVNGY8aMMYw5nU4NHDhQiYmJOaoTAAoKmjgA\nkI9iY2M1ZMgQj/FJkyYpLCws23mDf/9d1V56STdOmqRm82arxOnTKh0WkptSAQDIE7F9+ynp+npu\nYzWWLpVysO14x44d1bRpU8PY4cOHNXPmzBzVCAAFBU0cAMhHEyZM0D///GMY69Chg5o1a5b9pC6X\naixfLsv/v/mtsOsr3fzQOPnabLkpFQCAvOHjozMLHnEbCjtwQJGffZbtVBaLRZMnT1ZoaKhh/Jln\nntHXX3+dozIBoCCgiQMA+WTz5s1as2aNYSwiIsLjLeFXU+rrr1Xyxx/dxqJnz5NyuLMVAAB5LbH5\nbYrr1MVtrPqKFbKmpmY7V3h4uMaPH28Yc7lcGjJkiJKyuZU5ABQUNHEAIB+cP39eI0aM8BifMmWK\ngoODs53XkpamGi++6DYW06KlEtt3yHYuAAC86eyc+XJdctdowJkzqvj22znK1bp1a7Vq1cowdvjw\nYc2ZMydHeQEgv9HEAYB8MHHiRJ06dcow1qVLF9188805ylth0yYFXvJ4lstq1bkFi7kLBwBQ4KXW\nqKXzQ4a7jVV+9VX5nj+fo3zjxo3zuK7cE088oW+//TZHeQEgP9HEAQAv++ijj/Tyyy8bxsqUKaMH\nHnggR3ltcXGqsm6d21hUv/5KrXt9jvIBAOBtUZOnKr1EiYxjW2Kiqnl49PhqSpQooXHjxhnGnE6n\nBg8erOTk5BzlBoD8QhMHALwoLi5OI0eO9Bh/6KGHFBgYmKPcVV9+Wb4XL2YcO4KCFXPZtq0AABRk\nzpLhipo8zW2s3JYtCvrzzxzla9WqlW677TbD2G+//ab58+fnKC8A5BeaOADgRVOnTtXff/9tGOvW\nrZsaNmyYo7wBx4+r/KZNbmNnxk1UeunSOcoHAEB+OT9kuFJq1Mw4tjidqrFsWY62HLdYLBo3bpzH\n3aoee+wxff/99zmuFQC8jSYOAHjJ559/rhdeeMEwVqZMmUzv0LmaGi++KGt6esZxUoVKihuVs92t\nAADIV76+OjN3odtQiZ9+UuDx4zlKFx4errFjxxrG0tPTNXjwYKWkpOQoNwB4G00cAPCChIQEDR06\n1GN84sSJOX6MqsQPPyhi1y63sbOz58nl75+jfAAA5Lf4Dp2U0Py/j0GdatlWW1au1cVKlXKcr02b\nNrr11lsNY7/++qsWLlxoGAOAgoYmDgB4waxZs/Snh+f5O3bsmOPdqJSerprLlrkNxTZsrIQ7e+Us\nHwAABYHFotOPPKZjb2/Sj8+vUPI1dRTnyP7jVP9LZ9GECRMUEhJiGF+8eLF+/PHHHOcHAG+hiQMA\neeybb77R008/bRgLDw/P8W5UklT2448VfOSI29i5hY+ypTgAoNBLqXOdElu2VqnQYPkGhSjZalda\nujPH+UqVKqUxY4wfNf73sarU1NQc5wcAb6CJAwB5KDk5WUOGDJHLw2KMmf1WMCsSq1VTbO3aGcfR\n3Xsq+aYc3tUDAEABFBIYIH8/u/yCQxXryF2u9u3bq2nTpoaxn3/+WYsXL87dBACQx2jiAEAeWrBg\ngQ4ePGgYa9OmjZo3b56r/HHXXadPn3pee+YsUkLVajo/d0Gu8gEAUBBFhobIFhAoh6+fkhzpV7/A\ng38fqwoKCjKML1q0SPv3789xfgDIazRxACCP/PDDD1qyZIlhLCwsTA8++GCu50hxpCvVHqDTd96l\ng1/slqNizhd9BACgoPL3syvI309+IWGy7zugKi+9lONckZGRHh+rSktL09ChQ5WenvNGEQDkJZo4\nAJAH0tLSNGTIEI9vAseOHasSJUrkep5Yp1V+IaEK9PdTQGBArvMBAFBQlY+L0c2zpqrtxLGq9sor\nCvv55xzn6tChg5o0aWIY+/bbb7V06dIc5waAvEQTBwDywJIlS/SzhzeXt956q1q3bp3rORLS0uWy\n+8vXP0CRYTlfVwcAgMKg8tgHVGHrlozjGsuWSc6cLXRssVg0ceJEBQQY/wJkxowZ+uuvv3KUGwDy\nEk0cADDZ/v37NX/+fMNYcHCwxo8fL0tOd49yueR3+rScLpcuunzkFxKm0EB/+dpsuagYAICC7+zD\nc92OQw8fVplt23Kcr3Tp0ho+fLhhLCEhQSNHjvS4MQEA5BeaOABgovT0dA0ZMkRpaWmG8dGjRysi\nIiLH+SM//1xNBgxQ5eeXyt+RLpvdT6VCuQsHAFD0JTW5RbHd7nQbq7ZqlaxJSTnO2b17d9WtW9cw\ntnXrVr366qs5zg0AeYEmDgCY6Pnnn9eePXsMYzfddJM6dOiQ49zW1FRVX7FCVodDNTe+o8739FKN\nb7+W1cqPcgBA8XB21lw57faMY//oaFV6880c57NarZoyZYp8fX0N4+PHj1dUVFSO8wOA2XjnDwAm\nOX78uGbOnGkYCwgI0MSJE3P+GJWkCu+8o4DTpzOObQkJsl13XY7zAQBQ2KRVrabzIx9wG6u0YYPs\nuWi0VKlSRf379zeMnTt3TuPHj89xbgAwG00cADCBy+XSAw88oISEBMP4iBEjVLZs2Rzn942JUZX1\n693GogYMVto1tXOcEwCAwih6/CQ5Lnk02ZacrOqrV+cqZ79+/VStWjXD2GuvvaYtW7YYxgDA22ji\nAIAJ3nzzTX344YeGseuvv17dunXLVf6qa9fKlpiYcZwWGqoL02bkKicAAIWRMzRMUVPd73wtu3Wr\ngg8dynFOX19fTZ482eMds/fff78uXryY4/wAYBaaOACQS+fPn9fYsWMNYzabTZMmTcrVujVBR4+q\n/ObNbmNnJj6k9PBSOc4JAEBhFtN/oJKvreM2VmP5cikXu0ldd9116tWrl2Hs77//1owZ/PIEQP6j\niQMAuTRlyhSdPXvWMHbvvfeqatWqucpfY/lyWZzOjOPEKlUVN/z+XOUEAKBQs9l0Zt4it6GSP/+s\niK++ylXaIUOGqEyZMoaxpUuXateuXbnKDwC5RRMHAHLhs88+00svvWQYq1y5su65555c5Q/fs0fh\n333nNhY1d6F0yc4cAAAURwlt2im+TTu3seovvCBLWlqOc/67EYERl8ulYcOGKSUlJcf5ASC3aOIA\nQA4lJSVpxIgRHuOTJ0+WPRfNFkt6umosW+Y2dqFJMyV06ZrjnAAAFCWn5z8il49PxnHgyZOq8O67\nucp58803q3379oax3377TYsXL85VfgDIDZo4AJBDCxcu1B9//GEY69q1q2644YZc5S+3ebOC/vor\n49hlsejcwkekXGxTDgBAUZJa+1rF3Dco4zimeg1dqFEj13lHjx6tEiVKGMYeeeQR/frrr7meAwBy\ngiYOAOTAL7/8oscee8wwVqpUqUzv0MkKn/h4VV2zxm0sulcfpdzYMFd5AQAoaqIemqmUmrW0f8Gj\n+uyVN3X0+ga5zhkWFqYxY8YYxtLS0jRy5Eg5L1mvDgC8hSYOAGRTenq6hg8fLofDYRgfO3asgoOD\nczVHlfXrZY+NzTh2BAQoZs78XOUEAKAoSo+I0JGvv1Pq0OGyBYUq3e6vJEfuGyxt2rTRLbfcYhjb\ntWuXVq1ales5ACC7aOIAQDYtXbpUe/bsMYzdeuutatGiRa7yW9LSFPnll25jZx8YK0fZcrnKCwBA\nkWW1ys/XV8EBfvILDlOc0yJnLrYblySLxaIJEyYoICDAMD516lSdPn06V3MAQHbRxAGAbDh+/Lhm\nzJhhGAsMDNS4ceNkyeWaNS5fX327apV+vW+wHP4BSi5TVrEPjs9VTgAAioOIsBDZ/P1l8QtUggl3\n45QuXVrDhw83jF24cMHjTlYAkFdo4gBAFrlcLo0ePVoJCQmG8eHDhysyMtKUueJtdu0fMkI7Nn+q\nf1a8JFdQkCl5AQAoymw+PioRGCB7SJgSZJPvmTNSenqucnbr1k21a9c2jL3++uvaunVrrvIDQHbQ\nxAGALHrrrbe0efNmw1jdunXVrVs3U+ZxulyKl01+IWHyr1JFqc2am5IXAIDiIDwkSAFpqbrxlZd1\ny4ABKvfRR7nK5+Pjo0mTJslqNf7oNGrUKCUmJuZqDgDIKpo4AJAFsbGxGjdunGHMZrNl+uYuuy6m\nOeUTECRfu5/CQ3O3QDIAAMVN0K6v1PqOtrr2lTXySUtT1dWr5ZPLJkutWrXUq1cvw9jRo0e1cOHC\nXOUHgKyiiQMAWfDwww97XLywX79+qlatminzONKdSrT4yh4UovDgQNMaQwAAFBep1arLdsmjz34X\nLqjya6/lOu/gwYNVunRpw9jjjz+uX3/9NddzAMDV8OkAAK7i+++/19KlSw1jlSpVUv/+/XM9R4V3\n3lGFd9/VxRSH7MEh8rPbFRpovBsGAADwzFGhos498KDbWMU335RfLneSCggI8HhXrsPh0MiRI+V0\n5n4xZQDIDE0cAMhEenq6Ro4cKZeHbUonTpwou92eqzns0dGqvmqVaj37rNqMGqEK33+niNBgWbgL\nBwCAHIkeM15ppctkHPukpan6ypW5ztusWTO1aNHCMLZr1y6tWrUq13MAQGb4hAAAmVi6dKl++OEH\nw9jtt9+uG2+8MddzVFu9Wj7JyZKksON/qeGc6QpOT8t1XgAAiitXcLCiZsx2GyuzY4dCDxzIde4H\nH3xQgYGBhrGpU6d6fPwaAMxAEwcAPDhx4oQefvhhw1hISIjuv//+XM8R/PvvKnvZ1qRnp0yTMzgk\n17kBACjOLtx9j5Kur+c2VmPpUsnD3bVZFRkZqaFDhxrPeeGCJk6cmKv8AJAZmjgA4MGECRN08eJF\nw9jIkSNVsmTJ3E3gcqnGsmWyXPJmMqFGLcUNHpa7vAAAQPLx0ZkFj7gNhR04oMjPPst16u7du6t2\n7dqGsddff12ffPJJrucAACM0cQDAwEcffaS33nrLMFa3bl116tQp13OU+vprlfzpJ7exqPmLJJst\n17kBAICU2Pw2xXXq4jZWfcUKWVNTc5XXx8dHkyZN8riL5KhRo5SUlJSrOQDACE0cALhMYmKiRo8e\nbRjz8fHRxIkTc731tyUtTTVeeMFtLKZFSyW275CrvAAAwN3ZOfPluuQXJAFnzqji22/nOm+tWrXU\nq1cvw9iff/6phQsX5noOALgcTRwAuMyiRYt09OhRw9hdd92l6tWr53qOCps2KfDEiYxjl9WqcwsW\nSxZLrnMDAID/Sa1RS+eHDHcbq/zqq/I9fz7XuQcPHqzSpUsbxh577DHt378/13MAwKVo4gDAJQ4c\nOKDHH3/cMFamTBndd999uZ7DFhurKi+/7DYW1a+/Uuten+vcAADgSlGTpyq9RImMY1tioqqtWZPr\nvAEBARo3bpxhzOFw6IEHHpArlwspA8ClaOIAwP9zuVwaNWqU0tKMt/ceO3asAgICcj1P1XXr5Bsf\nn3HsCApWzGXboAIAAPM4S4YravI0t7HwXd/Ix4R1a5o1a6YWLVoYxnbu3KlXX30113MAwL9o4gDA\n/1u3bp127txpGGvevLmaNWuW6zkCjh9X+U2b3MbOjJuodA+3YgMAAHOcHzxMKdVrKN3up0ODhunD\nVWuV5u9vSu4HH3zQ4y96Jk2apAsXLpgyDwDQxAEASefOndPkyZMNY/7+/nrwwQdNmafGiy/Kmp6e\ncZxUoZLiRo0xJTcAAMiE3a4Ty1fqj6/36PeJ05ReqrTi05ympI6MjNSgQYMMY2fPntXDDz9syjwA\nQBMHACRNnTpV0dHRhrHMFi3MjhJ79ypi1y63sbOz58ll0m8BAQBA5pIbNlZ61WoqERQoe3CoEiw2\npTvNaeT07NnT4+YHy5cv1969e02ZB0DxRhMHQLH39ddfa/Xq1YaxGjVqeNw+NLsSK1fWqQ7/20I8\ntmFjJdxpTm4AAJB1JYMDZbfb5RsYrDiHOQsP22w2jR8/3jDmdDr1wAMPyGlSwwhA8UUTB0Cx5nA4\nNHr0aMOYxWLRxIkT5ePjY8pcqZGR+nbiFG1btU7nGjfRuYWPsqU4AAD5wGK1qlRosHyDQpRstSst\n3Zzmyg033KCOHTsaxvbs2aNVq1aZMg+A4osmDoBibdmyZfr5558NY127dtV1111n2lwOp1NJVl8l\nNmqi39/epOSbbjYtNwAAyJ6QwAD5+9nlFxCkkpu3qLJJu0iNGDFCwcHBhrFp06YpKirKlHkAFE80\ncQAUW6dPn9asWbMMYyVKlNCwYcNMnS82TbIHhcrP7qvQoEBTcwMAgOyr/suPajvkHjV++glVXbtW\n/idO5DpnyZIlNXz4cMNYTEyMpk6dmus5ABRfNHEAFFsPPfSQ4uLiDGMjR45USEiIaXMlO9KVavOT\nb2CQSoealxcAAORQaqqqThqrsMOHJElWh0PVX3zRlNRdunTRtddeaxhbs2aNvv76a1PmAVD80MQB\nUCzt3LlTr7zyimHs+uuv1+23327KPMF//CG5XIpzWuUXEqpAfz/5+/uZkhsAAOSC3a4zD89xGyr9\n5ZcK8/CYdXb4+Pho/PjxsnhY+27UqFFyOBy5ngdA8UMTB0Cxk5aW5nExY6vVqnHjxslqzf2Px5AD\nB9R4+HDVnTJFoSdOyNc/QJFh3IUDAEBBEdfzLiU1aOg2VmPZMsmEXaRq166tbt26Gcb27dun5557\nLtdzACh+aOIAKHaWLl2qX3/91TDWo0cP1axZM/eTuFyquWyZJCly7151GDZQddevka/NlvvcAADA\nHFarTi941G0o9PBhldm2zZT0Q4cOVYkSJQxjs2fP1gkT1uABULzQxAFQrJw6dUqzZ882jJUsWVKD\nBw82ZZ7Izz9X2P79GccWp1OWm5uYkhsAAJgnqcktiu12p9tYtVWrZE1KynXukJAQ3X///Yax+Ph4\nTZo0KddzACheaOIAKFamTJmiixcvGsZGjRrlcUvQ7LCmpqr6ihVuY+fbtldSq9a5zg0AAMx3dtZc\nOe32jGP/6GhVevNNU3LffvvtqlevnmHsjTfe0KeffmrKPACKB5o4AIqNzz//XK+++qphrF69emrX\nrp0p81R45x0FnD6dcey02XRu/iOm5AYAAOZLq1pN50c+4DZWacMG2aOicp3bYrFo/PjxHtfbGz16\ntFJTU3M9D4DigSYOgGIhK4sZe9pBIjt8Y2JUZf16t7GoAYOVdk3tXOcGAAB5J3r8JDkiIjKObcnJ\nqr56tSm5q1WrprvuusswdvjwYT399NOmzAOg6KOJA6BYePbZZ3XgwAHDWM+ePVW9enVT5qm2Zo1s\niYkZx2mhobowbYYpuQEAQN5xhoYpaupMt7GyW7cq+NAhU/IPHDhQEZc0iS41f/58FjkGkCU0cQAU\neSdOnNDcuXMNY+Hh4Ro0aJAp8wQdPapyH37oNnZm4kNKDy9lSn4AAJC3YvoPVPK1ddzGaixbJrlc\nuc4dEBDg8a7ghIQETZkyJddzACj6aOIAKPImT56s+Ph4w9ioUaMUFBRkyjw1li+XxenMOE6sUlVx\nw413pAAAAAWQzaYz8xa5DZX85RdFfPWVKelbtmypBg0aGMZef/117dy505R5ABRdNHEAFGk7duzQ\nhg0bDGM33nij2rZta8o84d9+q/DvvnMbi5q7ULpkpwsAAFDwJbRpp/g2/9vs4K+WrRVbvYYpuS0W\ni8aOHSsfHx/D+JgxY+RwOEyZC0DRRBMHQJGVlpamMWPGGMZ8fHw0duxYUxYztqSnq8by5W5jsTc3\nVUKXrrnODQAAvO/0/EeUeFMTffPKW/rukf/oTEQZ03JXrVpVPXv2NIzt27dPyy97TwEAl6KJA6DI\nev755/Xbb78Zxnr37q1q1aqZMk+5zZsV9NdfGccui0XRixZLJjSIAACA96XWvlbHtmyT7bbb5BsY\nohSbn9LSnVe/MIsGDhyokiVLGsZmz56ts2fPmjYXgKKFJg6AIunMmTMeFzOOiIjQfffdZ9pcJffu\ndTuO7tVHKTc2NC0/AADIH0GBAQrw85VfcKgumPiUU1BQkEaOHGkYu3DhgmbMYGdLAMZo4gAokqZP\nn664uDjD2KhRoxQYGGjaXPvnzdOuh+cqvkJFOQICFDNnvmm5AQBA/oosESqbf6DS7f5Kcph3N077\n9u1Vt25dw9jq1au1Z88e0+YCUHTQxAFQ5OzZs0dr1qwxjNWrV0+tW7c2db7kdJeOt26nz9/9WEc2\nbJSjbDlT8wMAgPzj5+ur4AA/+QWHKc5pUeAff5iS12q1Zro+35gxY+R0mtc0AlA00MQBUKQ4nU6P\nixlbrVY9+OCDpixmnDGfy6U4p0X2kDAFhIYovdmtpuUGAAAFQ0RYiMJOn1Lz+XN18/DhVzxKnVPX\nXHONunY13gjhu+++8/hLKQDFF00cAEXKyy+/rO8u2+r7X926dVPNmjVNnS/R4ZTLL0C+/gGKDAsx\nNTcAACgYItetUauenVTh652SpBrLlknp6abkHjJkiEJDQw1j06ZNU0xMjCnzACgaaOIAKDJiY2M1\nbdo0w1hoaKgGDx5s6nxOl0vxsskvOExhAf6y2Wym5gcAAAVD0o0NZHX8b2Xj4D//VLmPPjIld1hY\nmIYOHWoYi46O1uzZs02ZB0DRQBMHQJExb948j1tyDh061ONvubKr9KefqtZTTykl6rx8AoLk6+en\n8NBgU3IDAICCJ7lBI124q6/bWNXVq+WTmGhK/i5duqhWrVqGsWXLlumXX34xZR4AhR9NHABFwoED\nB/Tcc88ZxmrWrKkuXbqYMo81OVnVV6xQhfffV9vBA3Xd22+qlK+PrFZ+nAIAUJSdnTlHzoCAjGO/\nCxdU+bXXTMnt4+OjsWPHGsb+Xe/P5XKZMheAwo1PHQAKPZfLpXHjxslxyW3Olxo7dqx8fHxMmavS\nm2/KPypKkmRPTFCdZc8oPJZn1QEAKOocFSrq3AMPuo1VfPNN+Z0+bUr+66+/Xh06dDCMffnll3r9\n9ddNmQdA4UYTB0Ch99577+nTTz81jLVt21Y33HCDKfPYo6NV+bI3UGeHDJejeg1T8gMAgIItesx4\npZUuk3Hsk5am6itXmpZ/xIgRCgwMNIw99NBDSkhIMG0uAIUTTRwAhVpSUpImTpxoGPP399fIkSNN\nm6va6tXySU7OOE4tGa4LU6aalh8AABRsruBgRc1wX2i4zI4dCj1wwJT84eHhGjRokGHsxIkTWrJk\niSnzACi8aOIAKNQef/xxHTt2zDA2YMAARUZGmjJP8OHDKrt1q9vY2SnT5AwrYUp+AABQOFy4+x4l\nXV/PbazG0qWSSWvW3HnnnapSpYphLLP3PQCKB5o4AAqtv/76S4sXLzaMlS9fXr179zZnIpdLNZYv\nl+WSN2cJNWopbvAwc/IDAIDCw8dHZ+YvchsKO3BAkZ99Zkp6m82mMWPGGMaSk5P10EMPmTIPgMKJ\nJg6AQmvKlClKvuTxpkuNGTNGdrvdlHlKff21Sv70k9tY1PxFks1mSn4AAFC4JLZoqYsdO7uNVV+x\nQtbUVFPyN27cWM2aNTOMvfXWW/riiy9MmQdA4UMTB0Ch9Nlnn+mtt94yjDVp0kRNmzY1ZR5LWppq\nvPCC21hMi5ZKbG+8ewQAACgezsxdINclv9AJOHNGFd9+27T8DzzwgGwefmE0btw4paenmzYXgMKD\nJg6AQsfhcGjcuHGGMZvNptGjR5s2V4VNmxR44kTGsctq1bkFiyWLxbQ5AABA4ZNao5bODxnuNhb2\n3femrY1ToUIFj4+G//zzz1q9erUp8wAoXGjiACh0Vq9erX379hnGevfurUqVKpkyjy02VlVeftlt\nLKpff6XWvd6U/AAAoHCLmjxV6SVKKLlsOX03Z5F2PPKYqb/o6d+/v0qWLGkYmzlzpi5cuGDaXAAK\nB5o4AAqVCxcu6OGHHzaMlSpVSgMGDDBtrqrr1sk3Pj7j2BEUrJjLthUFAADFl7NkuP56Y6MOfbVH\np3r2Ubp/oBLTzHvMKSgoSMOHDzeMRUdHa8GCBabNBaBwoIkDoFBZsGCBoqOjDWPDhg1TYGCgKfME\n/P23ym/a5DZ2ZtxEpZcubUp+AABQNCQ3bCzfsDCF+PvLLyRMF11WOU16pEqSOnTooGuuucYw9uyz\nz+rQoUOmzQWg4KOJA6DQOHz4sJ599lnD2LXXXqvbb7/dtLlSypTRn0OHKjUwSJKUVKGS4kYZb/cJ\nAAAQGRYsXz9/WfyDFJ/mNC2v1WrVgw8+aBhzOByaOHGiaXMBKPho4gAoNCZPniyHw2EYGz16tKxW\n836kOe12/darjz569S0d63OPzs5dIJe/v2n5AQBA0WL18VGJoEDZg0OVYLEp3WleI+f6669X27Zt\nDWNbtmzRli1bTJsLQMFGEwdAobBt2zZ98MEHhrE2bdro+uvNXWzY6XIpwWKTq3JV/f3I40ro0dPU\n/AAAoOgpGRwou92uQIdTlZcuVzkP711yYuTIkfL38AuliRMnKjU11bS5ABRcNHEAFHgOh0MTJkww\njPn5+WnEiBGmzxmX5pRPQJDsdj+FhwSZnh8AABQ9lvR0XffOBnXq11O1Nr6taqtWyXbJJgm5ERkZ\nqX79+hnGDh06pKVLl5oyD4CCjSYOgAJvxYoV2r9/v2Gsb9++KlOmjKnzOZxOJVl8ZQ8OVXhIkCwm\nPqYFAACKLtu5c6r82COyx16QJNnj4lTllVdMy5/Z+5558+bp7Nmzps0FoGDikwmAAi0mJkazZxtv\n6x0REaG7777btLnC9u2TJTVVsWmSPThUfnZfhQaZs9sVAAAo+hxlyyp6rPvdwxU2bpT/iROm5Pfz\n89PIkSMNY7GxsZo1a5Yp8wAouGjiACjQ5s+fr3PnzhnGRowYoYCAAFPm8TtzRvUmT9ZNgwap9K5v\n5BsQqMjQEFNyAwCA4uPcqDFKK18h49jqcKj6iy+alr9Vq1aqV6+eYWzlypX66aefTJsLQMFDEwdA\ngXXw4EE9//zzhrE6dep43KUhJ6qvXCmf1FQFnjqlFvMf1s0zJinA38+0/AAAoHhwBQbqzKy5bmOl\nv/xSYT//bEp+i8WiMWPGyGKxXDm3y6Vx48bJ5XKZMheAgocmDoACa9KkSR63FB8zZoxpW4qHHDig\nMtu3u42ltWtvSm4AAFD8xPW8S0kNGrqN1Vi2TDJp2/FatWqpc+fOhrGdO3fq7bffNmUeAAUPTRwA\nBdLHH3+sLVu2GMbatWun6667zpyJXC7VXLbMbSj+2ut08d77zMkPAACKH6tVpxc86jYUeviwymzb\nZtoUQ4cOVVCQ8Q6aU6dOVXJysmlzASg4aOIAKHDS0tI0ceJEw5jZW4pHfv65wi7b+SpqwWLJx8e0\nOQAAQPGT1OQWxXa7022s2qpVsiYlmZK/ZMmSuu8+4186HT16VM8995wp8wAoWGjiAChwXnjhBf32\n22+GsX79+ikyMtKUeaypqaq+YoXb2Pm27ZXUqrUp+QEAQPF2dvY8Oe32jGP/6GhVevNN0/Lfeeed\nqlSpkmFs4cKFioqKMm0uAAUDTRwABcr58+c1Z84cw1jp0qXVt29f0+aq8M47Cjh9OuPYabPp3PxH\nTMsPAACKt7QqVXV+5ANuY5U2bJDdpOaKr6+vxy3H4+LiPL6nAlB40cQBUKDMnTtXMTExhrERI0bI\n39/flHl8Y2JUZf16t7GoAYOVdk1tU/IDAABIUvT4SXJERGQc25KTVX31atPyN2vWTA0aNDCMvfji\ni9p/2WPjAAo3mjgACozffvtNyy5bZPhfdevWVZs2bUybq+ratbIlJmYcp4WF6cK0GablBwAAkCRn\naJiips50Gyu7dauCDx82Jb/FYtEDDzxguOW40+nUlClTTJkHQMFAEwdAgTF58mSlp6cbxsaMGWP4\n5iQngo4eVfnNm93Gzkx8SOnhpUzJDwAAcKmY/gOVfG0dSZLDP0C/Dhik+IoVTctfs2ZNdezY0TD2\n0UcfaevWrabNBSB/0cQBUCB8+umnHrcUv/3223XttdeaNleN5ctlcTozjhOrVFXcMOPnyQEAAHLN\nZtOZeYsU0/ceff7BpzowfJTibH6mTjFkyBCPj51PmjRJDofD1PkA5A+aOADyXXp6uiZNmmQY8/f3\n17Bhw0ybK/zbbxX+3XduY1FzF0qX7BwBAABgtoQ27XTq+RcUUL2a7MFhSrDYlO50mZY/IiJC/fr1\nM4zt379fq01chwdA/qGJAyDfvfzyy/rll18MY3fffbdpW4pLUvCRI3JZ//ej70KTZkro0tW0/AAA\nAJkpERwoP7tdvkEhik1zXv2CbOjTp4/H902zZs1SXFycqfMB8D6aOADyVXx8vGbOnGkYi4iIUJ8+\nfUyd7/g992j7shd1+uZb5LJYdG7RYsmktXYAAACuxmK1KiIkSL6BIUqx+Skt3bxGjr+/v4YPH24Y\ni4qK0iOPPGLaXADyB00cAPnq8ccf1+nTpw1jQ4cOVUBAgKnzpaU7FVWjtr598WXt+2iHUuobb8kJ\nAACQV4ICAxTg5yu/4BDFpqQrzMMdyTnRtm1b1a5d2zD21FNP6ejRo6bNBcD7aOIAyDcnTpzQ448/\nbhirWbOmbr/9dtPnjHVIfsGh8vezy9aoken5AQAAsiIyLETlv/tO7R8YofoTJijw+HFT8lqtVo0e\nPdowlpqaqunTp5syD4D8QRMHQL55+OGHlZSUZBgbNWqUrFZzf0QlO5xy+PrJFhCoyNAQU3MDAABk\nR9Vpk3XLg8MV9tcxWZ1OVV++3LTcN9xwg1q2bGkYe+ONN7Rr1y7T5gLgXTRxAOSLn376SS+//LJh\nrGnTpmrYsKF5k7lccrpcinNaZA8JU5C/n/z92I0KAADkn/hWbdyOI3bvVsm9e03LP3z4cPn6+hrG\nJkyYIKfT3EWVAXgHTRwAXudyuTRp0iS5XFduq2m1WnX//febNlfYL7/oxgkT5HvgoFx+AfL1D1Bk\nGHfhAACA/HWxa3cl3nyL21iNZcuk9HRT8leoUEE9e/Y0jO3Zs0dvvPGGKfMA8C6aOAC87sMPP9SO\nHTsMY926dVPlypXNmcjpVI1ly1Ti55/V/MHRavqfJYqMjZHNZjMnPwAAQE5ZLDq9cLHbUPCff6rc\nxx+bNkX//v0VFhZmGJs6darHx9oBFFw0cQB4VVpamqZMmWIYCwoK0sCBA02bq8z27Qo9dEiSZHG5\nVHnzeyp9Psq0/AAAALmR3KCRLtzV122s6urV8klMNCV/cHCwBg0aZBj7+++/9dRTT5kyDwDvoYkD\nwKtWrlypgwcPGsbuvfdelShRwpR5rMnJqrZypdvYuU53KLlZc1PyAwAAmOHszDlyBgRkHPvFxKjy\na6+Zlr9r166qUqWKYWzx4sU6ffq0aXMByHs0cQB4TWxsrObMmWMYK1OmjHr16mXaXJXefFP+Uf+7\n68bpa9e5uQtMyw8AAGAGR4WKOvfAg25jFd98U34mNVd8fHw0atQow1h8fLzmzp1ryjwAvIMmDgCv\neeSRRxQdHW0YGzFihOx2c3aMskdHq/Lrr7uNnR0yXI7qNUzJDwAAYKboMeOVVrpMxrFPWpqqX3ZH\ncW7cfPPNaty4sWFs1apV+u2330ybC0DeookDwCuOHTump59+2jBWp04dtW7d2rS5qq1eLZ/k5Izj\n1JLhujBlqmn5AQAAzOQKDlbUjNluY2V27FDogQOm5LdYLHrggQdktV758S89PV1Tp/I+CSgsaOIA\n8Irp06crNTXVMPbAAw/IYrGYMk/w4cMqu3Wr29jZKdPkDCthSn4AAIC8cOHue5R0fT23sRpLl0ou\nlyn5q1Wrpo4dOxrGPvjgA33xxRemzAMgb9HEAZDnvv32W23YsMEw1rJlS11//fXmTORyqcby5bJc\n8mYnoUYtxQ0eZk5+AACAvOLjozPzF7kNhR04oMjPPjNtisGDB8vf398wNnnyZDmdTtPmApA3aOIA\nyFMul0sTJ040jPn6+mrEiBGmzRXx9dcq+dNPbmNR8xdJNptpcwAAAOSVxBYtdbFjZ7exoD/+MC1/\nRESE7rrrLsPY999/rzfeeMO0uQDkDZo4APLUxo0btWvXLsPYnXfeqfLly5syjyUtTdVfeMFtLKZF\nKyXebnzbMAAAQEF0Zu4CuWw2nW90k7avWq8fBg41Nf/dd9+tkiVLGsZmzJihlJQUU+cDYC6aOADy\nTFpamqZNm2YYCw0NVf/+/U2bq8KmTQo8cSLj2GW16tyCR0zLDwAA4A2pNWrpz0936s+NmxXf+Gal\n2PyU6kg3LX9gYKAGDRpkGDt27Jief/550+YCYD6aOADyzIoVK/SHh1uA77vvPoWEhJgyj098vKq8\n/LLbWNQ9A5Ra16S1dgAAALwope71CgwMUKCfXX7BoYpNN2cDiH916dJFlStXNowtXLhQ58+fN3U+\nAOahiQMgT8TFxWnevHmGsQoVKqhbt26mzZUeFKTfZsxQXKX/vhlxBAUr5rJtOgEAAAqbyLAQ2QIC\nlW73V2KaeXfj+Pj4eFyX8MKFC1q0aJFhDED+o4kDIE88/vjjioqKMowNHz5cvr6+5k1msejETTfr\no9Wv6Jdpc3RqxmylR0aalx8AACAf2H19FRLgL7+QMF10WeU0abtxSWrWrJnq1atnGHv++ed19OhR\n0+YCYB6aOABMd/LkST3xxBOGseuuu0633XabqfM5XS7FOa2ylyil6EFDdXHE/abmBwAAyC+RocHy\n9fNX2KkzqvvQVIXv3m1KXovFolGjRhnGUlNTNWPGDFPmAWAumjgATDdnzhwlJSUZxu6//35ZLOY+\n153gcMriFyibv78iSpizzg4AAEBB4BsTo0aPzleHIfeqzPffqcby5bI4HKbkvvbaa9WmTRvD2IYN\nG/Tdd9+ZMg8A89DEAWCq/fv366WXXjKMNW/eXDfccIOp8zldLiXIJntIqEoEBsjm42NqfgAAgPxk\nO3VSZV9/RRanU5IUdPy4yn3wgWn5hw0b5vEx98mTJ8tl4iNcAHKPJg4AU02bNk3O/3+TcSmr1arh\nw4ebNk/Yzz/LHh2tuDSnfAKCZLf7KTwkyLT8AAAABUHKDfV0oV9/t7Gqa9fKFh9vSv5y5cqpR48e\nhrGdO3fqAxMbRgByjyYOANN8/vnn2rx5s2Hsjjvu8LiVZXb5JCaq7rx5unnAAFV/7TUF+PgqPCRI\nFis/0gAAQNETNX2WnIH/+2WVPS5OVV55xbT8/fv3V3BwsGFs6tSpcpj0+BaA3OMTDwBTOJ1OTZky\nxTDm7++vgQMHmjZX5ddflz0mRrbkZNV7+SW17tdDoXYTd7sCAAAoQBxlyyp67AS3sQobN8r/xAlT\n8oeGhmrAgAGGsYMHD2rVqlWmzAMg92jiADDFW2+9pe+//94wdvfddys8PNyUefzOnFHFN990G4vr\ndqdk5pblAAAABcy5UWOUVr5CxrHV4VD1F180LX+PHj1UtmxZw9icOXN08eJF0+YCkHM0cQDkWkpK\niqZPn24YK1mypPr06WPaXNVXrpRPaur/5o6M1IWJxncAAQAAFBWuwECdmTXXbaz0l18q7OefTclv\nt9s1bNgww9jZs2f1+OOPmzIPgNyhiQMg11544QUdPXrUMDZo0CAFBASYMk/IgQMqs32729jZaQ/L\n5eEZbgAAgKIkruddSmrQ0G2sxrJlksGmEjnRunVr1a5d2zD2xBNP6OTJk6bMAyDnaOIAyJULFy5o\nwYIFhrFKlSqpS5cu5kzkcqnmsmVuQ/HXXqeL995nTn4AAICCzmrV6QWPug2FHj6sMtu2mZTeqvvv\nv98wlpiYqPnz55syD4Cco4kDIFeWLFmic+fOGcZGjBghHx8fU+aJ/Pxzhe3f7zYWtWCxZFJ+AACA\nwiCpyS2K7Xan21i1VatkTUoyJf+NN96oZs2aGcZWrVqlQ4cOmTIPgJyhiQMgx/7++289/fTThrEb\nbrhBt956qynzWFNTVX3FCrex823bK6lVa1PyAwAAFCZnZ8+T027POPaPjlalyzZ+yI0RI0bIar3y\no2J6erpmzpxp2jwAsi/Pmzhff/11Xk8BIJ/Mnj1bycnJhrH7779fFovFlHkqvPOOAk6fzjh22mw6\nN/8RU3IDAAAUNmlVqur8yAfcxipt2CD7+fOm5K9SpYo6depkGHvnnXf07bffmjIPgOzL8yZOixYt\nVLduXT355JOKjo7O6+kAeMkvv/yil19+2TDWsmVLXXfddabM4xsToyrr17uNRQ0YrLRrjBfdAwAA\nKA6ix0+SIyJCkpRQvoL2TJ6q1JIlTcs/cOBA2S+52+dSU6dOlcvlMm0uAFnnlcepDh48qClTpqhi\nxYrq27evPvnkE29MCyAPefrH28fHx+P2lDlRde1a2RITM47TwsJ0YdoM0/IDAAAURs7QMJ2Zs0An\nZ83V5+99or/bdlCCw5xdqiQpMjJSvXv3Nox98cUX+vjjj02bC0DWeXVNnNTUVL399tvq1KmTqlWr\npoULF+rEiRPeLAGACbZv3+7xH+5u3bqpYsWKpswTdPSoym/e7DZ2ZuJDSg8vZUp+AACAwiz27v9j\n767DpCrbMIDf07OznWzBLkt3l6RIIyVIN4gYfCqKYtCdEtLdgoqggiAoIaCUgJSEdGx3T5zvj4Vx\nhj2zMTPb9++6vJzzPmee884us7vnmTcGIPZ/Y+Hk5gKlsysSBRkMdhwh069fPzg7O4vGPvnkE+j1\nertdi4hyJs+LOO+//z48PT3NPrEXBAH379/HpEmTEBwcjM6dO2Pv3r38IUBUBAiCgPHjx4vGNBoN\nBg0aZLdrqZ8+hc7JyXicHBSM+JFv2i0/ERERUXHg6eIEhVINiYMGiVr7jcZxcnLCwIEDRWOXL1/G\n9u3b7XYtIsqZPC/iLFy4EI8fP8bXX3+Ntm3bGhc6ff5/vV6PAwcO4LXXXkNgYCA+/fRT3L59O6+7\nRURW+vbbb3Hu3DnRWL9+/eBux7nYUS+9hMPrN+HG631hkCsQMXk6YGFuNhEREVFJJZXJ4O7oAKWT\nK5IkcugN9huN0717d/j4+IjGvvjiC4ubXBBR3siX6VQKhQK9e/fGwYMHcefOHXzxxRcIDAzMNDon\nLCwMc+fORaVKlfDyyy9j+/btSEtLy48uElEOaLVai9tKenh4oGfPnna9nt5gQJyLO66Pn4Tzv51E\nUucuds1PREREVFy4OWmgUiqhcHRGSmQM3P76yy55lUolhg0bJhp78OABVqxYYZfrEFHO5OuaOABQ\npkwZTJ06Fffu3cP+/fvRo0cPyOVyAP+NzhEEAcePH8egQYPg7++P9957D3///Xd+d5WIXrB+/Xrc\nunVLNDZkyBA4ODjY9XrxWgFyjROUSiU0lSoCdtqynIiIiKi4kUil8FbKUfnbXWg3fAiqTZwIRVyc\nXXK3bdsWwcHBorEZM2Ygzk7XIaLs5XsR5zmJRIIOHTrgu+++w6NHjzBnzhxUrFgx0+icmJgYfPXV\nV6hTpw4aNmyINWvWIDExsaC6TVRiJScnY8qUKaKxwMBAdOrUya7X0xkMSJUpoHB0hqezIyTSAvtx\nRURERFT4GQyo1qsrqn85B8qkRCiSkhC0aZNdUstkMowaNUo0FhUVhXnz5tnlOkSUvUJxV+Tt7Y1x\n48bh+vXrOH78OAYPHmz2ib4gCBAEAefOncPo0aPh5+eHkSNH4o8//ijAXhOVLEuWLMHTp09FY8OH\nDzeOqLOZIWMxvlgtoHJyhVqlhLOjxj65iYiIiIorqRTxPcyntvvv3QvNgwd2Sd+4cWPUrFlTNLZw\n4UKLfycSkX0ViiKOqWbNmmHjxo14+vQpli9fjnr16gEwn2qVlJSEDRs2oFmzZqhevTqWL1+OhISE\nguw2UbEWHR2N2bNni8YqVKiAli1b2uU66idP0HDwYLgf/AU6mQJyBw28XcS3tSQiIiIic9FvjEZ6\nULDxWGowIMROa9ZIJBKLo3FSUlIsjtgmIvsqdEWc55ydnTF48GC89dZbKF26NARBgEQiMf4HZBR0\nrl27hjFjxiAoKAjTpk3j6uhEeWD27NkW5zqPGjUKUjtNdQpZvRqax49Ra/YstHv/HfjduAa1irtR\nEREREeWEoFIhbOJUszavP/+E+/nzdslfrVo1NG/eXDS2du1a3Lhxwy7XISLLCmUR58yZMxg1ahT8\n/Pzwxhtv4NGjR2aFm+f/ARkVYUEQEBsbi8mTJ6NmzZq4cuVKQXafqFh59OgRli5dKhqrW7cu6tev\nb5fruP79N3yOHTMee1y9jFJhHJZLRERElBsJXbohuWFjs7Zyy5cDer1d8o8cOVL0Azy9Xm9xF1Mi\nsp9CU8SJjo7G4sWLUbNmTTRp0gTr1q1DQkKCWdFGrVZj8ODBOHnyJK5cuYKxY8fCy8sLwH/FnNu3\nb+OVV15BWFhYAb8iouJh8uTJFke4WRpSm2sGQ8YfFyYSatRCYp9+9slPREREVFJIJAidPsusyenO\nHfgdOGCX9GXKlEHHjh1FY9999x1Onz5tl+sQkbgCL+IcPnwYffv2RUBAAMaOHYsrV66Y7VAFZAzb\nW7x4MZ48eYKNGzeiSZMmqFq1KubPn49Hjx5h7dq1CAgIMJ4fGRmJ+fPn5/dLISp2rl+/jg0bNojG\nWrZsiUqVKtnlOqV+/RUuLwy/jZg+C+COVERERES5llqnHmJf72PWFrxuHWTJyXbJP2TIECiV4lPe\nP/nkk0z3c0RkPwVyh/T48WNMmzYNISEhaN++Pb755hukpaUB+G8BY5VKhUGDBuHEiRO4fPkyxowZ\nA1dX10y5FAoFhg8fjr///hvVqlUDkDHlat++ffn3goiKqc8//xyGZ7tFmZJKpRgxYoRdriFNTUXZ\nNWvM2qI6vorUl5rZJT8RERFRSRT++SQY1GrjsSomBmW2b7dLbm9vb/Tq1Us0duzYMRyw06gfIsos\n34o4er0eu3fvRqdOnRAcHIzJkyfj3r17ZlVaQRBQpUoVLFq0CE+ePMGmTZvw0ksv5Si/m5sbJkyY\nYDy+d++evV8CUYny559/4vvvvxeNde7cGaVLl7bLdUrv2gV1RITx2KBQImrydLvkJiIiIiqpdAGB\niHp7jFlb4K5dUIWG2iV/v3794OwsvovoJ598Ar2d1uAhInN5XsS5ceMGxo0bh4CAALz++us4ePCg\n8Q1tOupm4MCB+P3333HlyhX873//g5ubW66vVbNmTePj5yN7iCj3BEHA+PHjRWMqlQqDBw+2y3WU\nkZEos2OHWVv4iFHQhYTYJT8RERFRSRY55gNofUoZj2VaLUJeGAFtLScnJwwcOFA0dvnyZWy306gf\nIjKX50WcKlWqYOHChQgPD8806qZy5cr48ssv8eTJE2zevBlNmza16VoODg62dpeIABw4cADHTHaK\nMtWzZ0/jguK2KrtuHWQmiyanu3sg9qOP7ZKbiIiIqKQTnJwQ8dlEs7ZSv/0Gl2vX7JK/e/fu8PHx\nEY198cUXFjfHICLr5dt0KtNRNwMGDMDx48dx9epVvPfee1aNuhEjl8tRpkwZBAUFoUyZMnbJSVTS\nGAwGfPrpp6IxZ2dn9Otnnx2jnG7ehO/Bg2Zt4ePGw+DqZpf8RERERATE9u2PlOr/zVjQajRQPXli\nl9xKpRLDhg0TjT148ACrVq2yy3WI6D/5UsQRBAGVKlXCwoUL8fjxY2zZsgXNmtl/0dKAgADcu3cP\nd+/exd27d+2en6gk2LFjBy5duiQaGzBgAJycnGy/iCCg3IoVkJiMzksqVwHxw0banpuIiIiI/iOT\nIWzqDAhSKe693h8/79iN2y1etlv6tm3bomzZsqKxGTNmICEhwW7XIqJ8KOL0798fx44dw7Vr1/D+\n++/D3d09ry9JRFZKT083WyDclLe3N7p3726X63idPAn3ixfN2iKmzgDkcrvkJyIiIqL/JDdvidvn\n/sbTOfMhlA5GskQOvcE+24DLZDK88cYborGIiAgsWrTILtchogx5XsTZunUrmjdvnteXISI7WL16\ntcVRbEOGDIFKpbL9IoKAsmvXmjXFNG+F5HYdbM9NRERERKK0pcvAxVEDpVIJpaML4rQGu+Vu3Lgx\nqlevLhqbP38+oqKi7HYtopIu39bEIaLCLTExEdOmTRONlSlTBh062KnIIpHgyrRpeNK4CQBAkEoR\nNW2mfXITERERkUUSqRTeLk6QOzohTa5Cut4+hRyJRGJxNE58fDxmz55tl+sQEYs4RPTM813kxIwc\nORIymcxu14r3D8CxaXNwctUmPPrkC6RXE//khoiIiIjsS+OghkalhMrJBXE6AAb7FHJq1qyJRo0a\nica++uorPH782C7XISrpWMQhIkRERGD+/PmisapVq9p9IfJYHaBydkFS8xZIGPuRXXMTERERUda8\nXZ0hVzvA9/Rp1B86FI537tgl74gRI0TbU1NTMXXqVLtcg6ikYxGHiDBr1iyLOwe88cYbkEgkdrtW\nik4PvVINudoR3q7OdstLRERERDnjfOMftHhjEJpP+gxODx+i3PLlgGD7QscVKlRAq1atRGPr1q3D\nrVu3bL4GUUnHIg5RCffw4UMsX75cNNaoUSPUrl3bbtcyCALiDVKonFzhpFZBpVTaLTcRERER5Yzi\n0UO4nT1tPPY4fx4ep09n8YycGz58OKTSzLeZer0eEydOtMs1iEoyFnGISrhp06YhLS1NNDZy5Ei7\nXMP52jW4XL2KJK0BEpUGcrUaXm4chUNERERUEBLbd0RSsxZmbeVWrIBEp7M5d+nSpdGxY0fR2Ndf\nf42LFy/afA2ikoxFHKIS7NatW1i/fr1orHXr1ihfvrztF9HrUWnBAtR9913UnDkDbgkJcNM4QG7H\nhZKJiIiIKBckEoROnQnBZMq844MH8PvxR7ukHzJkCBQKhWjs888/t8s1iEoqFnGISrBJkyZBr9dn\napdKpRg2bJhdruF74ACcni2WF3TsCF7p9Sp8ksXX3yEiIiKi/JFWoyZi+w00awveuBHyxESbc3t7\ne6N79+6isf379+PEiRM2X4OopGIRh6iEunTpEnbs2CEa69ixIwIDA22+hiw5GSHr1pm1RXd8FXo/\nf5tzExEREZFtIj6dAIPG0XisjI9H0JYtdsk9YMAAaDQa0dhnn30GwQ4LKROVRCziEJVQEyZMEG1X\nKBQYPHiwXa5RZscOKGNijMd6lQoxk7i9JBEREVFhoPP1ReT/PjBrC9i9G+rHj23O7erqit69e4vG\nfv/9dxw4cMDmaxCVRCziEJVAf/zxB360MOe5W7du8PHxsfkaqrAwBO7aZdYWPupt6AJL25ybiIiI\niOwj6q13ofUPMB5LdTqErFpll9yvv/46XF1dRWOfffYZDAaDXa5DVJKwiENUwgiCgM8++0w05uDg\ngAEDBtjlOiFr1kCWnm48TvP2RuzYcXbJTURERET2IWg0CJsw2azN5/ff4Xrpks25NRqNxb8tL168\niG+++cbmaxCVNCziEJUwv/76K44ePSoa69WrF9zc3Gy+hvO1ayj1669mbeHjv4Dg5GRzbiIiIiKy\nr/jXXkdKnbpmbeWWLwfsMFImq1HeEyZMgFartfkaRCUJizhEJUhWo3CcnZ0tzlvO5UVQfvlys6bE\nylWRMMA+6+wQERERkZ1JpQidNtusyeXmTZQ6dMjm1Eql0uJ6i7du3cLGjRttvgZRScIiDlEJsmfP\nHpw9e1Y01q9fPzjZYaSM99GjcL161awtYvosQCazOTcRERER5Y2URo0R17WHWVvZ9esh0ettzt2h\nQweULi2+LuKUKVOQkpJi8zWISgoWcYhKCL1ejy+++EI05uHhgR49eojGckOano6Q1avN2qLbtENK\ny5dtzk1EREREeSt84hQYlEoAQFiDRvh98nQIdvggTiaTYfjw4aKxx48fY/kLo7iJyDIWcYhKiO3b\nt+PatWuisUGDBkGtVtt8jYDvvoNDaKjx2CCXI2rqTJvzEhEREVHe0wYFI3zSNNzauA2nV21GZMWq\nSNPbZwepFi1aoEKFCqKxWbNmIT4+3i7XISruWMQhKgHS09MxadIk0Zifnx86d+5s8zUUMTEI2rrV\nrC188HBoK1S0OTcRERER5Y/oUW9B27kLNBo1VM4uiNdL7JJXKpVi5MiRorGoqCgsWLDALtchKu5Y\nxCEqAdatW4e7d++KxoYOHQqFQmHzNZSxsUj19TUea11dETtefBFlIiIiIircvF2doVBrYFCqkaS1\nfV0cAGjQoAFq1qwpGlu4cCEiIiLsch2i4oxFHKJiLjk5GdOmTRONBQUF4ZVXXrHLdZLKlsXxZStw\n5sNPkOrphbAPP4HB3cMuuYmIiIgofynkcrg4qKB0dkWiIINBEGzOKZFI8MYbb4jGEhMTMWfOHJuv\nQVTcsYhDVMwtW7YMT58+FY2NGDECMjvtGmUQBCRIlXjcdxDO/PI74keMskteIiIiIioYni5OUCjV\nkDhoIL1+A66XLtmcs3r16mjSpIlobNmyZXjy5InN1yAqzljEISrG4uLiMHv2bNFYpUqV0KxZM7td\nK1Grh0TtAIVKDY8AX+DZzgZEREREVDRJZTKUSoxDo/lz0PLdt1Fp7lxItFqb844YMQISSea1dlJT\nUzFjxgyb8xMVZyziEBVjCxcuRHR0tGhs5MiRor88raE3GJAEBZROrnDTaCC10+geIiIiIio40rhY\n1O3QCkE/7IZEEKB58gQB339vc95y5crh5ZdfFo2tWbMG9+7ds/kaRMUVizhExVRERAQWLlwoGqtd\nuzbq1atn8zUk6ekAgHitAIWjE5RKJdydNTbnJSIiIqKCZ3B1Q1zP183agjZvhiIuzubcQ4YMgVSa\n+XZUq9Vi6tSpNucnKq5YxCEqpmbPno3ExETRmKUhrLkhT0xEo0GDUGbNGujSdFA4OsPT2RESkV/G\nRERERFQ0RXz8OfTOLsZjRVISgjZtsjlvmTJl0K5dO9HYpk2bcPPmTZuvQVQc8W6LqBh69OgRli1b\nJhpr0qQJqlevbvM1ymzdCnV4OEK2b0eXYQNQ9uBPcHbkKBwiIiKi4kTv5YXIsePM2vz37oXmwQOb\ncw8ZMgRyuTxTu8FgwOTJk23OT1QcsYhDVAxNnz4daWlporHhw4fbnF/95AkCd+/+7zg6Cl6RETbn\nJSIiIqLCJ/qN0UgPCjYeSw0GhKxYYXNeX19fdOrUSTT29ddf4/LlyzZfg6i4YRGHqJi5c+cO1q1b\nJxpr3bo1ypcvb/M1QlavhtRkZ4JUXz/EjXnf5rxEREREVPgIKhXCJpqvU+P1559wP3/e5twDBw6E\nUmRXU0EQMHHiRJvzExU3LOIQFTPTpk2DTqfL1C6VSjF06FCb87v+/Td8jh0zawv/fBIEDadSERER\nERVXCV26IblRE7O2kOXLAb3eprze3t7o1q2baGzPnj04d+6cTfmJihsWcYiKkZs3b2Lz5s2isfbt\n26N06dK2XcBgQLnly82a4mvWQmLvvrblJSIiIqLCTSJB6LSZZk3Od+7A78ABm1P369cParVaNDZh\nwgSb8xMVJyziEBUjkydPhsFgyNQul8sxePBgm/OX+vVXuNy4YdYWOX02wB2piIiIiIq91Dr1EPt6\nH7O24HXrIEtOtimvu7s7evbsKRo7cOAATpw4YVN+ouKEd15ExcSVK1fw9ddfi8Y6deoEX19fm/JL\nU1NRds0as7aojq8itUlTm/ISERERUdER/vkkGBwcjMeqmBiU2b7d5rx9+vSBo6OjaOzzzz+HIAg2\nX4OoOGARh6iYmDRpkugvN4VCgYEDB9qcv/SuXVBH/LcDlUGhRNTk6TbnJSIiIqKiQxcQiKi3x5i1\nBe7aBVVoqE15nZ2d0adPH9HY8ePH8euvv9qUn6i4YBGHqBi4cOECdpts+W2qW7du8Pb2tim/MjIS\nZXbsMGsLHzEKupAQm/ISERERUdET+e770Jb6b5R3UqlSUMTG2py3Z8+ecHFxEY1xNA5RBhZxiIoB\nS9svqtVq9OvXz+b8Zdetgyw11Xic7u6B2HGf2JyXiIiIiIoewckJ4Z9NhM7dHZc/mYADG3YgtFwF\nm/NqNBr0799fNHbmzBn89NNPNl+DqKhjEYeoiPvzzz8t/kLr0aMHPDw8bMrvdPMmfA8eNGsL//hT\nGFxcbcpLREREREVXXJ9+uH3mImJGvgmluycSBRkMdhgp061bN4t/v06YMEF0Ew+ikoRFHKIiztIo\nHI1GY3FecW4EbdsGickv5KRyFRA/dITNeYmIiIioCJPJYHBzh4eLE+RKJWQOjkjQ2l5gUavVFtdz\nvHTpEr777jubr0FUlLGIQ1SEHT9+HIcOHRKN9ezZE66uto+W+efjj3GzT1/olUoAQMTUGYBcbnNe\nIiIiIir6pFIpPJ00UDq5IFkih95g+2iczp07o1SpUqKxiRMnQq/X23wNoqKKRRyiIkoQBHzxxRei\nMScnJ/Tu3dsu10l3cMD5EaPx6+79uDfuUyS362CXvERERERUPLg4aqBUKqF0dEGc1gCJVmtTPqVS\niUGDBonG/vnnH2zbts2m/ERFGYs4REXU4cOH8fvvv4vG+vTpAycnJ7tcJ04rQOHoDH1wCJI+4mLG\nRERERGROIpXC28UJSpkc5b/+Go369YMiOtqmnB06dEBAQIBobPLkydDaWCgiKqpYxCEqggRBwIQJ\nE0Rjrq6ueO211+xyHa3egDSZEgqNM7ycHSGR8kcGEREREWVW6vBBtOnRATU3roU6KgplN2ywKZ9M\nJsPQoUNFY3fv3sX69ettyk9UVPGOjKgI2r9/P06fPi0a69evHzQajV2uE6sDVM4ucFAp4KhxsEtO\nIiIiIip+FE8ew+HpE+Ox3/79cLxzx6acL7/8MoKDg0Vj06ZNQ2pqqk35iYoiFnGIipisRuF4eHig\nW7duNuV3ePAAvvv2ISUtHXqlGnK1I7xdnW3KSURERETFW/SwkUgLKWc8lhgMKLd8OWDDtuMymQzD\nhg0TjT1+/BirVq2yOjdRUcUiDlER8/333+PChQuisQEDBkCtVtuUv9yqVag8fz4av/02Aq7/Aye1\nCqpnO1MREREREYlSKhE2ZYZZk8f58/CwMHo8p5o3b44KFSqIxmbPno3k5GSb8hMVNSziEBUher0e\nEydOFI35+Pjg1VdftSm/2/nz8Dp1CgDgfudfNH9nBIKu/21TTiIiIiIqGRLbd0RSsxZmbeVWrIBE\np7M6p0QiwYgRI0RjoaGhWLlypdW5iYoiFnGIipBdu3bh6tWrorGBAwdCacuIGb0e5ZcvN2uKq1sf\naU2bW5+TiIiIiEoOiQShU2dCkEiMTY4PHsDvxx9tStuwYUNUq1ZNNDZ79mwkJSXZlJ+oKGERh6iI\n0Ol0mDx5smjMz88PHTt2tCm/74EDcHph8bmoGXMAk1/CRERERERZSatRE7H9Bpq1BW/cCHliotU5\nJRKJxbVxIiIisGzZMqtzExU1LOIQFRFbt27FzZs3RWODBw+GXC63OrcsORllX9imMaJ7T6TWb2B1\nTiIiIiIqmSI+nQCDxtF4rIyPR9CWLTblrFu3LmrWrCkamzt3LhISEmzKT1RUsIhDVASkp6dj6tSp\norHSpUujbdu2NuUvs2MHVNHRxmO9SoWYSeLXIyIiIiLKis7XF5H/+8CsLWD3bqgfP7Y6p0QiwdCh\nQ0VjUVFRWLp0qdW5iYoSFnGIioANGzbg7t27orGhQ4dCJpNZnVsVFobAXbvM2sLffAe6wNJW5yQi\nIiKiki3qrXeh9Q8wHkt1OoTYuCV4nTp1ULt2bdHY/PnzER8fb1N+oqKARRyiQi41NRXTp08XjZUt\nWxatWrWyKX/ImjWQpacbj9O8vRH7wUc25SQiIiKikk3QaBA2YbJZm8/vv8P10iWb8loajRMTE4PF\nixfblJuoKGARh6iQW716NR49eiQaGzZsGKRS69/GzteuodSvv5q1hY//AoKTk9U5iYiIiIgAIP61\n15FSp65Zm61r49SqVQv16tUTjS1YsACxsbE25Scq7FjEISrEUlJSMGvWLNFYhQoV0KxZM+uTC0Km\nLcUTK1dFwoDB1uckIiIiInpOKkXotNkAAINcjpuv98Wf4z+3Oa2l0ThxcXH48ssvbc5PVJixiENU\niK1atQqhoaGiseHDh0Niw/bf3kePwvXqVbO2iOmzABvW1yEiIiIiMpXSqDFCp8zA3weO4NqnkxHv\n5gmdwWBTzurVq6Nhw4aisS+//BLRJht2EBU3LOIQFVLJycmYPXu2aKxKlSpo1KiR1bml6ekIWb3a\nrC26TTuktHzZ6pxERERERGKi3x4DRY0aUKtUUDi6IE4r2JzT0michIQELFiwwOb8RIUVizhEhdTK\nlSsRFhYmGhs6dKhNo3BkKSlIqFzZeGyQyxE1dabV+YiIiIiIsiKRSuHl4gSFgyPS5Wqk6W0bjVOl\nShU0btxYNLZkyRJERkbalJ+osGIRh6gQSkpKwpw5c0Rj1apVQ4MGDWzKr3V1xcXPv8ChRcsQU60G\nwgcPh7ZCRZtyEhERERFlRaNWQeOggsrZBfF66z+QfM7SaJzExETMnz/f5vxEhRGLOESF0IoVKxAe\nHi4as3UUznNxBgkSGjfDuV17ETNFfAtzIiIiIiJ78nZ1hkKtgUGhgusvh+B0+7bVuSpVqoSmTZuK\nxpYuXWrx72miooxFHKJCJikpCXPnzhWNVa9e3eKWirmRrNVDr1BD7qCBl7srBLXa5pxERERERNlR\nyOUI/OcK2r73NurMmolyX30FCNavkWNpNE5ycrLFv6mJijIWcYgKmeXLlyMiIkI0Zo9ROAZBQIIg\ng8rZFc5qNVQKhU35iIiIiIhySnXlMur06Q6Py5cAAO6XLsHrxAmr85UvXx4tWrQQjS1btgxPnz61\nOjdRYcQiDlEhkpiYaPETg5o1a6Ju3bpW55YlJWVcQ2uARO0AhUoNb1cnq/MREREREeVWWvUaSGzd\nxqwtZOVKSLRaq3MOGTJEtD01NdXiOpNERRWLOESFyLJlyyyupG/LKByJXo+677yDql98AemTUCid\nXOGm0UAqk9nSXSIiIiKiXAudOhOCyd+hmidPEPD991bnCwkJQatWrURjK1euxJMnT6zOTVTYsIhD\nVEgkJCRg3rx5orFatWqhTp06Vuf2++knON6/D5+TJ9HpjaGouWQ+3J0crM5HRERERGSt9EqVETN4\nqFlb0ObNUMTFWZ1zyJAhoh94pqWlYdasWVbnJSpsWMQhKiS++uorREVFicYsLdiWE/LERARv2GA8\nlup0cEpJhoSjcIiIiIiogER8/Dn0zi7GY0VSEoI2bbI6X3BwMFq3bi0aW716NR4+fGh1bqLChEUc\nokIgPj4e8+fPF43Vrl0btWvXtjp3ma1boTT5VEPnoEHshMlW5yMiIiIispXeywuRY8eZtfnv3QvN\ngwdW5xw8eDCk0sy3uOnp6Zg5c6bVeYkKExZxiAqBpUuXIjo6WjRmyygc9ZMnCNy926wt/J3/Qefr\nZ3VOIiIiIiJ7iH5jNNKDgo3HUoMBIStWWJ2vTJkyaNOmjWhs3bp1uHfvntW5iQoLFnGIClhcXBwW\nLFggGqtTpw5q1aplde6Q1ashNVnpP9XXD3Fj3rc6HxERERGRvQgqFcImTjVr8/rzT7ifP291Tkuj\ncbRaLWbMmGF1XqLCgkUcogK2ZMkSxMTEiMaGDRtmdV7Xv/+Gz7FjZm3hn0+CoNFYnZOIiIiIyJ4S\nunRDcqMmZm0hy5cDer1V+QICAtCuXTvR2MaNG3Hnzh2r8hIVFiziEBWg2NhYLFy4UDRWr1491KhR\nw7rEBgPKLV9u1pRQoxYSe/e1Lh8RERERUV6QSBA6zXy9Guc7d+B34IDVKQcNGgSZyCYeOp0O06ZN\nszovUWHAIg5RAVq8eDFiY2NFY7ashVPq8GG43Lhh1hYxYzYgMrSUiIiIiKggpdaph9jX+5i1Ba9b\nB1lyslX5/P390aFDB9HYli1b8O+//1qVl6gw4B0dUQGJjY3Fl19+KRqrX78+qlevblVeaWoqQtas\nMWuL6vgqUps0tSofEREREVFeC/98EgwODsbjqEqVrS7iAMDAgQMhl8sztev1eu5URUUaizhEBWTR\nokWIM9n625Qto3BK79oFVWSk8digUCJq8nSr8xERERER5TVdQCCi3h6D5CrVcGrlBhybMQ/xbu5W\n5/P19UWnTp1EY5s2beLaOFRksYhDVABiYmIsjsJp0KABqlWrZlVeZWQkyuzYYdYWPmIUdCEhVuUj\nIiIiIsovkR+Mw70jJ5DSqjVUzq6IN9h2u9q/f3+OxqFih0UcogLw5ZdfIj4+XjRmyygcv337IEtN\nNR6nu3sgdtwnVucjIiIiIsovgkoFyGTwdnWGQqWGoHRAkta6XaoAoFSpUujYsaNobNOmTbh7967V\nuYkKCos4RPksOjoaixYtEo01atQIVatWtTr3/UGDcPHj8Uj29gEAhH/yGQwurlbnIyIiIiLKb3K5\nHK4aB6icXZEgyGAQBKtzWRqNo9PpOBqHiiQWcYjy2cKFC5GQkCAaGzJkiE25DRIJbrzSHod378et\nL6Yifshwm/IRERERERUEDxcnyJVKyBwckaA1QJaUZFUeX19fiztVbdy4Effu3bOhl0T5j0UconwU\nFRWFxYsXi8YaN26MKlWq2JQ/UauHRK2B1NUdae+OAUQ+dSAiIiIiKuykUik8nTRwjU9ArdmzUH/k\nSEjT063KNWDAAMhkskztHI1DRRGLOET5aMGCBUhMTBSN2bIWDgDoDQYkSRRQOrvC3dEBUpFfVERE\nRERERUW5FUvwSs9OCD7yKxxCQxH47bdW5clqNM6GDRs4GoeKFBZxiPJJZGQkli5dKhpr0qQJKlWq\nZFP+OK0AhaMzVEol3Jw0NuUiIiIiIiposvh4yNLSjMdltm2DIjraqlwDBw60OBpn1qxZVveRKL+x\niEOUT+bPn29xFI61a+HI4+JQds0aCHHxSJOroNA4w8vZERIp39pEREREVLRFfPgx9G5uxmN5cjLK\nbthgVa6sRuOsX78e9+/ftyovUX7jnR5RPoiMjMRXX30lGnvppZesHoUTvHkzgrZvx0uDB6HKz/ug\nkQKOGgdbukpEREREVCgY3D0QMe5Tsza//fvheOeOVfmyWhuHo3GoqGARhygfLFiwAEkWVtS3di0c\nhwcP4L93LwBAFR+P2gtmo/K+PVb2kIiIiIio8IkeNhJp5cobjyUGA8otXw5Yse24n58f2rdvLxpb\nv349Hjx4YHU/ifILizhEeSwqKsriKJxmzZqhQoUKVuUtt2oVpHq98TgloDQSBw21KhcRERERUaGk\nUCBsygyzJo/z5+Fx+rRV6QYMGACpyNIDWq2Wo3GoSGARhyiPffnll3ZfC8ft/Hl4nTpl1hY+cQoE\ntdqqfEREREREhVViuw5Iat7SrK3cihWQ6HS5zuXv729xNM66des4GocKPRZxiPJQdHQ0lixZIhpr\n2rQpypcvLxrLkl6P8suXmzXF1a2PpB49rekiEREREVHhJpEgdMoMCBKJscnxwQP4/fijVekGDhxo\ncTTO7Nmzre4mUX5gEYcoDy1evBgJCQmiscGDB1uV0/fAATi9sJhb1Iw5gMkvNSIiIiKi4iStRk3E\n9h9k1ha8cSPkFv7Wzoq/vz/atWsnGlu7di0ePnxoVR+J8gOLOER5JDY2FosXLxaNNWnSBBUrVsx1\nTllyMsquX2/WFtG9J1LrN7Cqj0RERERERUXE+C9g0Dgaj5Xx8QjautWqXByNQ0UVizhEeWTx4sWI\ni4sTjVk7CqfMjh1QRUcbj/UqFWImTbUqFxERERFRUaLz9UXk/z4wawvYvRsOjx/nOldAQECWo3Ee\nPXpkVR+J8hqLOER5IC4uDosWLRKNNWrUCJUrV851TlVYGAJ37TJrC3/zHegCS1vTRSIiIiKiIifq\n7THQBgQaj6U6Hfy+/96qXJZG46Snp3M0DhVaLOIQ5YGlS5ciNjZWNGbtKJyQtWshS083Hqd5eyP2\ng4+sykVEREREVBQJDg4I+2ISACDNwxNnP/wEf48cZVWugIAAtG3bVjS2Zs0ajsahQolFHCI7S0hI\nwMKFC0VjDRo0QNWqVXOd0/n6dZQ6fNisLXz8FxCcnKzqIxERERFRURX/2usInTEH5w6fwOP+Q5Ao\nVcIgCFblymo0zpw5c2ztKpHdsYhDZGdfffUVYmJiRGNWjcIRBJRftsysKbFyVSQMsG5EDxERERFR\nkSaVInrUW3AN8INCqYJM44QErcGqVIGBgWjTpo1obPXq1XhsxXo7RHmJRRwiO0pMTMSCBQtEY/Xq\n1UP16tVznVOi1yO6QQPoVGpjW8T0WYBMZnU/iYiIiIiKOqlUCk8nDRSOzkiRKqAzWFfIGTRoEEfj\nUJHBIg6RHS1fvhxRUVGisSFDhliVU5DLcWfQYOzbsBUPunRHdNv2SGn5si3dJCIiIiIqFpw1DlCr\nVFA4uiBOa92UqsDAQLzyyiuisdWrV+PJkye2dJHIrljEIbKTpKQkzJ8/XzRWp04d1KhRw+rccVoD\ndEEhuDprIZ5u3GZ1HiIiIiKi4kQilcLLxQkKB0cYtAaUXrcOyoiIXOexNBonLS2No3GoUGERh8hO\nVq5ciQgLvzCs3ZEKANJ1eqTJVZA7OsHLxQkSpdLqXERERERExY1GIUf5fd+jy9D+KLd1K0LWrct1\njtKlS1scjbNq1SqOxqFCg0UcIjtITk7G3LlzRWM1a9ZE7dq1rc4dZ5BA5eQCjUoJRwd19k8gIiIi\nIipBXPZ8h6pffAJ1VCQAwPfgQTjduJHrPJZ2qkpLS7P4tz5RfmMRh8gOVq1ahfDwcNGYNWvhKGJj\nIdHrkazVQ69QQ+6ggZers63dJCIiIiIqduK7vYbUylXM2sotXw7kctvxMmXKoHXr1qKxVatW4enT\np1b3kcheWMQhslFKSorFynyNGjVQp06dXOesMnMm6o8YAccz56BydoWzWg2VQmFrV4mIiIiIih+5\nHGFTZpg1uf/9N7xOnMh1qkGDBkEikWRqT01Ntbj+JVF+YhGHyEZr1qxBaGioaGzw4MGivwSy4nH6\nNDzOnoXj/fto+cV4NH3vLZSSWbfSPhERERFRSZDUug0SW7cxawtZuRKS9PRc5clqNM6KFSssjr4n\nyi8s4hDZIDU11eJq9dWqVUO9evVylU+i16PcihVmbUqDAXBxtbqPREREREQlQejUmRBkMuOx5skT\nBOzZk+s8lkbjpKSkYOHChbZ0kchmLOIQ2WDdunUWV6q3ZhSO308/wfH+feOxIJEgavpMIJd5iIiI\niIhKmvRKlREzeKhZW9DmzVDExeUqT1BQEFq2bCkaW7ZsGaKioqztIpHNWMQhslJaWhpmz54tGqtc\nuTIaNGiQq3zyxEQEb9hg1hbRqw/SauV+TR0iIiIiopIo4uPPoXd2MR4rkpIQtGlTrvMMGjRItD0x\nMRGLFi2ytntENmMRh8hKGzZswKNHj0RjQ4YMyfUonDJbt0Jp8imBzkGD2IlTbOojEREREVFJovfy\nQuTYcWZt/nv3QvPgQa7yhISEoFmzZqKxJUuWIDY21touEtmERRwiK6Snp2PWrFmisUqVKqFRo0a5\nyqd+8gSBu3ebtYW/8z/ofP2s7iMRERERUUkU/cZopAcFG4+lBgNCXlh3MicsjcaJj4/H0qVLre0e\nkU1YxCGywqZNm/DAQjXfmrVwQlavhlSrNR6n+vohbsz7tnSRiIiIiKhEElQqhE2catbm9eefcD9/\nPld5KlasiMaNG4vGvvzyS8THx1vdRyJrsYhDlEtarRYzZ84UjVWoUAFNmjTJVT7Xv/+Gz7FjZm3h\nn0+CoNFY3UciIiIiopIsoUs3JDcy/7u83PLlgF6fqzyWRuPExMRg+fLlVvePyFos4hDl0ubNm3Hv\n3j3RWK5H4RgMGb9MTCTUqIXE3n1t6CERERERUQknkSB02n8fvOoVCjyp3wDSXBZxqlativr164vG\nFixYgKSkJJu6SZRbLOIQ5YJWq8WMGTNEY+XKlUPTpk1zla/U4cNwuXHDrC1ixmxAyrcmEREREZEt\nUuvUQ2zvvojq3BW/ff8zzr/xNtLl8lznGTx4sGh7ZGQkVq5caWs3iXKFd4pEubBt2zbcvXtXNJbb\nUTjS1FSErFlj1hbV8VWkNsldIYiIiIiIiMQ9WbwcYRu3Ql82BConF8Tpcp+jRo0aqFOnjmhs3rx5\nSElJsbGXRDnHIg5RDun1eotr4ZQtW9biFoSWeJw7B1VkpPHYoFAiavJ0m/pIREREREQmno288XFx\nhtzBEelyFVJ1uZtSBVheGycsLAxrXvhgligvsYhDlEO7du3CrVu3RGODBw+GNJdToCKbNcOfy5Yj\nvEYtAED4iFHQhYTY3E8iIiIiIjKnVqvgqFZB5eyKeIMUgiDk6vm1a9dGjRo1RGNz585FWlqaPbpJ\nlC0WcYhywGAwWFwLJygoCC1atLAq78PylXFizWZcWrISsR99bEsXiYiIiIgoC96uzlCo1BCUDkhK\n00IRHZ3j50okEoujcR4/fowNGzbYq5tEWWIRhygHvv/+e1y9elU0NnDgwFyPwgGAJK0eBqUaCgcN\n8HpvGFzdbOwlERERERFZIpfL4apxQMCNG2j67juoPmECkIsROfXr10flypVFY7NmzUJ6erq9ukpk\nEYs4RNkQBAHTp4uvVRMYGIiXX3451zkNgoBEQQalkyucHdRQWLFKPhERERER5ZwkLQ21//cmmo0e\nCvd/b8P12jX4HDmS8+dLJBZ3qnrw4AG2bNlir64SWcQiDlE29u3bh4sXL4rG+vfvD5lMluuciVo9\nJGoNFCo1vFycbOwhERERERFlR1CpMrWVXbUK0lysZ9O4cWNUqFBBNDZz5kzodFZsf0WUCyziEGUh\nq1E4pUqVQtu2bXOcS6LVouL8+VDfuYMkiQJKZ1e4OzpAakURiIiIiIiIci980jQIJqPgHcLDEfjd\ndzl+flZr49y5cwfbt2+3uY9EWWERhygLhw8fxunTp0Vj/fv3hzwX06AC9u6F/759aPjGG2i44is4\nJybAzUljr64SEREREVE20suVR/SIUWZtZbZty9Uix02bNkWIhV1lZ8yYAb0+91uYE+UUizhEWZg2\nbZpou5eXFzp06JDjPPK4OARt2gQAkBoMKPf9t6i+fiUkViyITERERERE1ov48GPo3dyMx/LkZJTN\nxe5SUqkUAwcOFI3dvHkTu3btsrWLRBbxDpLIguPHj+P3338XjfXt2xdKpTLHuYI3b4YiMdF4rHVy\nRuzHn9ncRyIiIiIiyh2Duwcixn1q1ua3fz8c79zJcY4WLVogKChINDZjxgwYDAab+khkCYs4RBZY\nGoXj7u6Ozp075ziPw4MH8N+716wt/L0PoPf2tql/RERERERknehhI5FWrrzxWGIwoNzy5Tneclwm\nk2HAgAGisatXr+L777+3Sz+JXsQiDpGIP//8E4cPHxaN9e7dG2q1Ose5yq1aBanJvNiUgNKIH/2u\nzX0kIiIiIiIrKRQIm2y+gYnH+fPw+PPPHKdo3bo1AgICRGPTpk2DkMOCEFFusIhDJMLSjlQuLi7o\n2rVrjvO4nT8Pr1OnzNrCJ06BkIsiEBERERER2V9i+45Iat7SrK3cypWQ5HCbcJlMZnFtnEuXLuHH\nH3+0uY9EL2IRh+gFf/31F/bt2yca69WrFzSaHO4opdej/PLlZk1xdesjqUdPW7tIRERERES2kkgQ\nOmUGBInE2OT44AH8c1F8adOmDXx9fUVjHI1DeYFFHKIXzJgxQ7Td0dERPXr0yHEevwMH4PTC4mhR\nM+YAJr8kiIiIiIio4KTVqInYfuajaYI2boQ8ISFHz5fL5ejfv79o7Ny5czhw4IDNfSQyxSIOkYkr\nV65g9+7dorHXXnsNTk5OOcojS05G2XXrzNoiuvdEav0GNveRiIiIiIjsJ+LTCTBoHI3Hyvh4eJ48\nmePnt2/fHj4+PqIxjsYhe2MRh8jEzJkzRdvVajV69sz5NKgyO3ZAGRNjPNarVIiZNNXm/hERERER\nkX3pfH0R+b8PAAAxVavj8KJluNembY6fr1Qq0bdvX9HYH3/8gd9++80u/SQCWMQhMrp58yZ27twp\nGuvWrRtcXV1zlEcVFobAXbvM2sLffAe6wNI295GIiIiIiOwv6u0xeLR6Pf769kckvNQCCQYpDLkY\nQdO5c2d4enqKxqZO5Ye5ZD8s4hA9M3PmTBgMhkztSqUSvXv3znGekDVrIEtPNx6neXsj9oOP7NJH\nIiIiIiKyP8HBAfE9esHb3RVytQMElQOSdZnvDSzJajTO8ePHcezYMXt1lUo4eUF3gKgwuHv3LrZu\n3Soae/XVV+Hh4ZHjXJHNmsH5ylVowkIBAOGfToCQw7V0iIioZBJ0OujTUmBIS4GgTYdgMADgGgpE\nRAWhlN4AvZMKBp0UcgmQ021JBg4ciKZNm0InskV5bGwsrl+/bt+OUr6QSCSQyWRwcnKCi4sLNBoN\nJAW4WQ2LOEQAZs+eDb1en6ldoVBYrKhbEtayJa7WfwlVf/kFgX+eQEL/QfbqJhERFUO6pATo46Mh\nlUggk2T8sSiRSZDz2wYiIrInlUwKQZBBEJQAhFz9NK5atSq0Wq1oTK/XQyaT2aWPlH8EQYBOp0Ns\nbCxiY2Ph5OSEgIAASKUFM7GJRRwq8R49eoQNGzaIxjp27Ahvb+9c5UvQGiBxdce9N94CPv8CUv6g\nJiIiC3TxMdAnxUMhlcLJyQkaRyeoNRrIZTJICuiPQyIiAvQGA7R6PSTJSdDERCPNxwfIwc9lg8GA\nO3fuiH5ArFKpUKFChbzoLuUhg8GA9PR0JCQkICYmBomJiXj8+DECAwMLZEQOizhU4s2dO1e0Wi6T\nydCvX79c5dIbBKRIFFA7ucDTScMCDhERWWTQaaFPiodSJoN3qVJwdsnZAvpERJT3ZIIBirBQKKOj\nIBEECHI50r28sn2eVCqFu7s7IiMjM8Xi4uKQnJwMjUaTF12mPCKVSqFWq6FWq+Hs7IwHDx4gMTER\nycnJcHR0zD6BvfuT71ckKkRCQ0OxZs0a0Vjbtm3h6+ubq3xxOgEKR2eolEq4OPKHMxERWWZIToRU\nIoGziwsLOEREhYw8IgKqqEhInu1QpYyOhsTCNKkXubm5WZxq8/TpU7v1kfKfWq2Gm5sbACA+Pr5A\n+sAiDpVoCxYsQGpqaqZ2qVSKAQMG5CiHPC4Oirg4pOv0SJMpIXd0gpeLE4fBExFRlvSpyZBJJCzg\nEBEVQjofHwjy/yauSAQBKpHRNWJkMpnxRv9FMTExSElJsUcXqYC4uLgAABITEwvk+rzLpBIrMjIS\nK1asEI29/PLLCAwMzFGesuvXo9GAASi18xs4KNXQqJRwdFDbs6tERFQcGfSQSAClSlXQPSEiohdJ\nZdD6+pk1KeLjIRX5AFiMh4eHxfVSQkNDbe4eFRylUgkAouse5QcWcajEWrRoEZKSkkRjAwcOzFEO\nx7t34f/TT5AnJaHW2lVo2/81BESF27ObRERUTAnPhugX1O4WRESUNb2nJwxq8w9nVeHhwLOf31nJ\najROVFQU0tLS7NFFKgDPi3NCDv4d5AX+1UAlUmxsLJYuXSoaa9GiBYKDg3OUp9yKFZAYDMZjiVwO\nlA2xRxeJiIiIiKhASaD1DzBrkaekQJ7DaTTu7u4cjVMMFcSOVKZYxKESaenSpRYXoho0aFCOcnic\nPg2Ps2fN2iImTweeDa8jIiIiIqKizeDsAr2zi1mbMiICMPkg1xKFQgFXV/F1zyIjI5Genm6XPlLJ\nwiIOlTgJCQlYtGiRaKxJkyYoX758tjkkej3KvbCeTmzjpkjq9Ko9ukhERERERIWENiAAphNnZFot\nFLGxOXquh4eHaLsgCAgLC7O9c1TisIhDJc7y5csRHR0tGsvpWjh+P/4Ix/v3jceCRIKo6TOBAh5a\nR0RERERE9iWo1NB7eZm1KaOiIMnBwrYKhcK4m9GLIiIioM3htuVEz7GIQyVKcnIyFixYIBqrX78+\nqlatmm0OeWIigjduNGuL6NUHabXq2KOLRERERERUyOhK+UGQyozHUoMByhxuOW5pNI7BYEB4ODdF\nodxhEYdKlDVr1iAiIkI0ltO1cMps3QplXJzxWOegQezEKXbpHxERERERFT6CXA6dbymzNkVsLKQ5\n2GVKpVLB2dlZNBYeHg6dTmeXPlLJwCIOlRhpaWmYN2+eaKxWrVqoWbNmtjnUT54gcPdus7bwd/4H\nna+fXfpIRERERESFk87LGwaTTUwkeLbIcQ5YGo2j1+s5GodyhUUcKjE2b96Mx48fi8ZyOgonZPVq\nSE3mrab6+iFuzPv26B4RERERERVmEil0JluO6+VyaJ2dAUHI4kkZ1Go1nJycRGPh4eHQ52B9HSKA\nRRwqIXQ6HebMmSMaq1y5MurWrZttDte//4bPsWNmbeGfT4Kg0dilj0REREQlxZ9/nMKwwYNQrXJF\neLo6Q6OUQ6OUo3KFcgXdtSKBX6+Co3d1g97ZBWk+pZBQvgJSXVyRfQkng6XRODqdzuKSD3lFIpFA\nIpEgODg4X6/7XGpqKsqXLw+JRIIhQ4bk+fVOnjxpfM0//fRTnl8vL8kLugNE+WHXrl34999/RWMD\nBw6EJLtdpQwGlFu+3KwpoUYtJPbua68uEhERUSFy/949VKlY3m75Bg4ajNXr1tstX1G2ZvUqvD/m\nXQg5GL1QUkyfmrG+opubG97933sF3BvKTnpIOQACJDo9AB30ej3kOdik1sHBARqNBsnJyZliYWFh\n8PHxgVRaMsZZzJs3D//++y9UKhWmTZuW59dr2rQpunXrhr179+K9995D27ZtoVKp8vy6eYFFHCr2\nDAYDZs6cKRoLCQlBkyZNss2hefAAmocPzdoiZswGSsgPWSIiIiJ7iIiIwPhxHxkLOG3atkXdevXh\n5uYGAHBxdS3A3hWcmdMzbmLLBAWxiFNkSCCTSiEIMugNBgiCkP0HwwA8PT1FizharRaRkZHw8fHJ\ni84WKuHh4Zg7dy4AYPjw4ShTpky+XHfixInYu3cv7ty5g+XLl+ODDz7Il+vaG4s4VOz98MMPuHr1\nqmhswIABOap2JwcH49SmTfDbuAXlf/4J0e07IbVJU3t3lYiIiAoJdw8PzJwtPhX7uXlzZiMmJgYA\nMHLUmwgJCbF4btVq1ezav6Lqt8OHkZKSAgDo3acvNm7ZWsA9IrKeTCqF3mCAVCqDXq/L8WgcBwcH\n4/vAVGhoKLy8vIr9aJxZs2YhMTERUqkUH330Ub5dt27dumjbti0OHTqEWbNmYdSoUXB0dMy369sL\nizhUrAmCgBkzZojGAgIC0LJlyxzninTxQMTnUxA28i34lA7I/glERERUZLm4uOD9sR9mec7KFcuN\nRZxer7+OFi1b5UPPiraHDx8YH7/UrFkB9qRoS07nltSFhVwmhVYQoDdIIeh0kEKAILd8my2RSODp\n6YlHjx5liqWnpyM6OhpeXl552WUAKLDpjDExMVizZg0AoEOHDlkWv/PC6NGjcejQIURERGD9+vUY\nM2ZMvl7fHop3iY9KvEOHDuHcuXOisX79+kEmk+UoT7regDSZCgoHR6jr14cuKNiOvSQiIiIqGVJT\nU42PHRwcCrAnRPYhlUghlUjgEB8Hp3t3ocrBduEajQZqtVo09vTp02K9XtS6deuQlJQEIGMqVX7r\n2rWrsUi2ZMmSfL++PbCIQ8WapbVwfHx80K5duxznidNLoHJ2gcZBBY26aC6ARURERAXv/r17xp2F\n2rdpDSBjLYzNmzai66udULFcWbg6OkCjlOP+vXsAgOPHjhqfM2pE9jc906dOMZ6/ZfOmHPXrr7/O\nY9yHY9GoXl2U9isFNycNypYJROcO7bBs6RLRNTxyyrT/z9d+AYA3R44wtj//7/lrfvF59njdYl97\nQRCwc8cOdO3cEeWCyxhfd59ePXH40C+5ep1//XUe4z/+CC81aoigAD+4aNTw8XBD/dq1MGrEcHz3\nzTdIS0sT7c9zD+7fz/Q1Me3vc7nZnSotLQ3r1q5Bj25dUL5sENydHeHv44X6tWvhww/ex8ULF7LN\nkddfO3sY887bxj4uWfRljp4TFRWFgFLe0CjlCCjljaioqFxfV6JNh9PtW9CEPoVUr4ciIQFSkalS\nZs+RSCzuVJWWlmYc4ZeVCxcu4N1330WdOnXg5uYGhUIBLy8vVK1aFa+88gqmTJmCU6dOWdy6PLvd\nqe7du2c8p1WrVgAyvufbt29H+/btERAQAJVKBT8/P/To0QO//JKz7/nGjRsBAI6OjujUqVO2548f\nP97Yj+xmUeh0OnTq1Ml4frt27aDVas3Okcvl6N69OwDg9u3bOHHiRI76XZiwiEPF1smTJ3HshS3B\nn+vTpw8UCkWO8iRp9TAo1VCoHeDt4mTPLhIREVEJ9/DBA7zcojlGvzESh3/5BY8ePsx005GXkpKS\nMGzwIDRr3AjLli7B5ct/IyoqCunp6QgLDcWR337DuA/HonqVSvjzj1P51q/8EB0dja6dO2LYkEE4\nfOgQnj55YnzdP/6wF107d8L4j7NfryM2NhYD+vZBs8aNsGTRIly88BciIiKg0+mQmJiIa9euYuuW\nzRg0oB/eG/NuPryy/5w9ewa1a1TDmLffwsGff8aTx4+RlpaG2NhYXLt2FSuWfYWmjRvif+++A50u\n51O07PG1My3SmRayrNWoUWPj4/MWRuK/aOrkScaCyecTJsLT0zPX1xUUCkBqvhiOKjwcyGY0jZOT\nE5RKpWgsq9E4giBg3LhxqFevHpYtW4aLFy8iLi4OOp0OUVFRuH79On777TdMnjwZTZs2xfXr13P9\nmsRER0ejffv2GDBgAH755Rc8efY9Dw0NxZ49e9C+fXt8+GHWU1CvXLliXKu0devWORqNN378eGPB\n6/jx4zh06JDFc0eOHImff/4ZANCgQQPs3r1b9J6vS5cuxsc7d+7Mtg+FDdfEoWLL0lo47u7u6Ny5\nc9ZPFgRUmjsXEU2aIKxRcyidXeHsoM5x4YeIiIgoO6mpqejdqycuXbwAHx8fdOjUGcHBwUhKTMQf\nf5zK0U43tkhMTES7V1rj4oW/AABKpRKt27RBjRo14eTkhLCwMBw6eBC3bt1E6NOn6NiuLX757Qga\nNGiYq+uEhJQzLhL96+FD+PXwYQBAr9d7o269embnulsYnWBvOp0OA/r2xrGjR1HK1xedOr+KMmXK\nIDEhAQcPHMCVK5cBAEsWLUKdOvXQp18/0TwRERFo+3Ir3Lx5w9hWq3YdNGveHN7e3khNTcWdf//F\nqVMn8ejhQxhMRkWYLp792fhPMtrc3THuk/GZrhMYWDrXr/HMmdPo3L6dceqKs7MzXu3SFRUqVkRy\nUhKOHj2Cc2fPQhAErF29CmGhofj6m2+z/Xdnr6+dvTVq/F8R59y5s9mef+XyZaxfm7E2S6VKlTFq\n9FtWXlkCrX8AVP/eNrbIU1MhT0iAzsXF8rOerY3z9OnTTLGUlBTExcUZd20ztXTpUsyfP9943LRp\nUzRq1AheXl7Q6XSIiIjA5cuX8ccff5iN/LKFTqdDr169cOTIEfj6+qJLly4ICgpCQkIC9u/fj8uX\nM77nCxcuRL169dC/f3/RPPv37zc+fj66Jztubm749NNPMW7cOADAhAkT0LZt20znjR8/Hps2ZYzA\nq1SpEvbv3w8nJ/EP4Fu0aAGpVAqDwYD9+/dj6dKlOepLYcEiDhVLf/31l7EK+6JevXpBpcp6SpTX\nyZPwO3AAfgcOwLd2XfwzfiI8WuV8EWQiIiKi7Jw9cwYAMHDQYHy5ZGm+75Iy5u23jAWctu3bY+Xq\ntfDz8zM7RxAEfLVkMcZ/PA5paWkYOmggLl6+mqsPtgJLlzYuEp2YmGgs4rRt3x6DBg+x06vJnT9O\nZYwqGjnqTcyZN99sRMDUGTPx8UcfYtnSjPUyZs2YLlqIEAQBQwb2NxZwfP38sH7jJrR6ubXouX+c\nOol///3X2Ga6ePbzIo5zDhbUzomUlBQMGzzIWMBp2qwZtu7YiVKlSpmd9/X27XjzjRHQarX48Ye9\nWLVyBUa/9XaWue3xtcsLFSpWhIeHB6Kjo3H3zh1ERUVlObLm44/GGqcazZ43D/IsFiM2NWrEcGzd\nstkufQaAKVOmiE4revr0KVxdXTMV1Z4XcBQKBfbv3482bdqI5k1KSsI333wDd3d3m/t48uRJABmL\nAi9cuNDsez5r1ix88MEHWLx4MQBg6tSpFos4prMkGjRokOPrv/vuu1iyZAkePnyI06dP48cffzQb\nTbN06VLMmZNREPX398fBgwezXBzazc0NFSpUwI0bN3Dnzh08fvwYAQFFZ+MaTqeiYsnSWjhOTk7o\n1q1bls+VaLUIWbnSeOxz8S/UWL4Y0hwugkxERGRvYmtk8L/i8Vlk02bNsGrtunwv4Jw/fw47v94B\nAGjQsCG+3b0nUwEHyBgtMOa99zHmvfcAAHfv3ME3RXD6gZgOnTphyVfLMk3pkEgkmDl7DgJLZ4x+\nuXnzBq49mwJiav++n3D0yBEAGX9jHjz0q2gB53nOl5o2y7ei1batW3D3zh0AgH9AAL7b80OmAg4A\n9O3fH7PmzDUez509C+np6dnmt/Vrl1caNGpkfHw+i9E4e/fsMX7v2nfsiPYdOuZ53yyxNFokKSkJ\n8fHxZm1RUVF4+PAhAKB9+/YWCzhAxpozQ4cOtVtxonPnzlixYoXo93zevHko/ex7fuPGDeOUqReZ\nbjhTo0aNHF9brVZjypQpxuOJEycap5vt2rUL77//PoCM4szBgwcRFBSUbc6aNWsaH589m/3IrcKk\nePz2IzJx/fp17N69WzTWo0ePbP9ICti7F5rHj43HglSKqKniU7OIiIiIbPHp51/k+bQpMatWrDA+\nnjh5SrYja/73/lgsWbQIALDvpx/Rf+DAvOxevpg0earFmEKhQOdXu2DViuUAgEsXL6JqtWpm56xe\n9d+HfmM/GocKFSvmTUetsM1kpMgnn34Glyym9Yx++x0sXvQlHj54gNCnT3H40C/o1PnVLPPb+rUD\ngBYtW9l9q/RGjRrj4LPR+OfPnUO79h0ynZOWlobPxn9s7OvsOfNydY1evXuLvh4AkMXHQZqYaDwW\nJBKke3gAWXwY3LRpU8jlctE1iZ6PxnnOdJHilGwWT7a36dOnW4wpFAp07doVy5YtA5Cx6HK1F75G\n8fHxCH+2c5eLi4voVLGsDBkyBAsWLMDVq1dx8eJFfPvtt/Dy8sKgQYNgMBjg4OCAH3/8EdWrV89R\nPtNCz61bt3LVl4LGIg4VO7NnzxZdCEytVqNnz55ZPlceF4egTea7GUT0H4T0ajn7YUBERESUUw4O\nDmjZ6uUCufbRI78ByFgHp0XLVtme7+/vD29vb0REROCvv87nce/yXilfX9SqXTvLcypUqGB8HBFh\nvm20VqvFKZNdbQYOGmzX/tkiLS0NF/76y3jc47Ws//6VSqXo3qMHlj6bDvPHyZNZFnFs/drlpYYm\nI3HOWRhdsXTxIuMopTffeguVKlfO1TXate8gWhwCAOh1UF+/BolJsSXd1RVpvr5Z5oyJiTEWOEwl\nJiYiISEBzs7OADJ22PXz88PTp0/x66+/YvHixXj77bfzfN1OX19f1M7me17RpIgp9lqejyACIDrq\nLztSqRQzZ840zqr45JNPjIuwy2Qy7Ny5E82aNctxPtM+mPatKOB0KipW7t69i23btonGunbtalbJ\nFhO8eTMUJtVzrZMzYj6baNc+EhEREQFA+fIVICuA6doxMTF49OymJT093bileXb/RUREAAAin/2/\nKCtTpky25zg9u3EGMm6mTT24f9+43oyvn59x+lBhcP/ePeOUqIDAwCzXBnmudu26xse3b9/O4kzb\nv3Z5qUHDRpBKM25xz5/PvENVaGgo5s2ZDQDw9PTEZ1/Y+e98mRw6X/MChSIuDtJsFhh2dXW1+LPg\nxYWPP/74Y+Pj999/H35+fhg4cCBWrVqFixcvwmAwWNl5y3IyPck5m++56dQwjUZjVT+6du1qLNTc\nvXvXmHPNmjVma+TkhOnsjISEBKv6U1BYxKFiZe7cuWbDDJ9TKBR4/fXXs3yuw4MH8N+716wt/L0P\noPf2tmsfiYiIiADAxdXyFJe8FB0VZdPznxcvijK1Wp3tOabT3F68MY6K/u9r6O3tY7+O2UFsbIzx\nsadn9gUcAPD0+m8B4JiY6CzPtfVrl5ecnZ1RtWrGNJ7wsDBjsfK5iZ9/ZrxhnzB5Sq6n9OSEztML\nBpNNVCTIfstxqVRq3Eb7RfHx8Wbvuffffx/Tpk0zfh+ioqKwbds2jB49GnXq1IGnpycGDx6MU88W\noLYHe3zPTaeL5XQRaTGDB5uPeps6dSqGDRuW6zymfdBqtVb3pyBwOhUVG0+ePMH69etFYx07dsz2\nU4hyq1ZBajrPNKA04ke/a9c+EhERET33fMRAfjO9mfL29sYHH35UIP0oLgpiTaOcsqZvhfn15ESD\nRo2M25yfO3vWOErq/Plz2LZ1CwCgWrXqGDHyDavy/3LwQLaLNUtSUyGPNi+Wpru6QhDZIbdt27ao\nUqUK3NzcEBUVJVoAefr0KcqXL288/uKLLzBy5Ehs374dhw4dwqlTp4yjUmJjY7FlyxZs2bIFQ4cO\nxZo1a2wqmtiL6eib1NRUq3JcvnzZbCQSACQnJ1uVy3RNofxeWN5WBf/dJLKThQsXiq6mL5VK0bdv\n3yyf63b+PLxeqFaHT5wCIQdVZyIiorxm78U/qWgxvakWW/fvRSnZ3NR4mGy7nJaWZpctrfOCvV+3\nPXl6/Pc1DA8Py7fr5oS7+38jOqKiInP0nKjI/woObm62b0ldkBo1bowN69YCyNihqvtrrwEAxo39\nwPjvaM78+VZPZfx21y67bjHu6emJKlWqQCqVwt3dHVEiI+ViY2ORnJxsVgjx9fXF2LFjMXbsWBgM\nBly6dAm//fYbdu3ahTNnzgAANm7cCH9/f8yYUfCbtHibzG6Ijs56tJeY+/fvo0OHDoiNjQUAyGQy\n6PV6LF68GGPGjIG/v3+u8pn2wbuIzbzgdCoqFqKiorDSZFtwU23atMl68Sy9HuWXLzdriqtbH0k9\nsl4EjoiIiCg/OJpsQZyT9UWyW6TTy8vLOEI5Pj4eVy5ftq2DecTer9uegoKDjZ/ehz59mmnaTkEq\nExQEpVIJAHj08CEiI7Mv5Fy6dMH42HRR4qKoUaPGxsfnnm0z/vX27fjzjz8AAK926YrWr1jemrsg\nubu7WxyhFxoaavF5UqkUderUwYcffojTp09j3rz/dtxauXJlvk5psyQgIMC4AHNoaKjoEhiWREZG\nol27dnjy5AmAjJFIb731FoCMETWTJ0/OdX8em+xGHBwcnOvnFyQWcahYWLx4sej8bIlEgv79+2f5\nXL8DB+D0bIX656JmzAGK+FBSIiIiKh58fEoZH9/OZivc9PR0HD92NMtzJBIJWr3c2ni8edMGm/qX\nV+z9uu1JLpejafPmxmNbR2Y8n+6SmxtbS1QqFerU/W+h4j3f787yfIPBgD3ff288bvzSSzb3oSBV\nrFQJ7u4Zo4ku/PUXEhMTMeGLzwBk7MY2a85cm/KvXrceyem6HP2n/fcOhLNnkXrzFqKjohEXF4f4\n+Hiz/wYMGGDMLZPJLK7TEx0dneNpSGPHjjUWGaOjo42LkhckmUxm3HZcr9dnu4D2c0lJSejcuTNu\n3rwJABgxYgSmTZuGzz//3Dgyaf369bhx40au+vPPP/8YH9eqVStXzy1oLOJQkRcfH4+lS5eKxpo3\nb57lauqy5GSUXbfOrC2ie0+k1m9g1z4SERERWSswMNA43P/q1Su49exmRszK5ctEt/d90VvvvGN8\nvGbVKpw9eybH/cnJ1CZ7yIvXbU+j3hxtfLxw/rxsC01Zeb6DamxMTDZn5swAky3P582ZneXuO6tX\nrcSD+/cBZOy01bZde7v0oaBIJBLUb9gQQMZ9wug3RuLxo0cAgHfeHYNyJmvL5DWdnx/SKlZCamBp\nQKmCLgdvHXd3d4vrEmU1GseUwWAwG9Hj4OCQo+fltUYmW8BfunQp2/O1Wi169uxpnB7WpUsXrFq1\nCkDGdLJ3nv0c0+v1+Oyzz3LcD0EQ8PfffwPIWLS5Zs2aOX5uYcAiDhV5y5cvN86NfNHAgQOzfG6Z\nHTugNPllqVepEDNpqj27R0RERGSzrt17GB+/PXqU6PSiTRs3YMLnObuRafJSU/R6vTeAjHVxunXu\nhO+++cZigUan0+HXw4fQu+dr2LtnT+5fgJXs/brtqWOnzmj18ssAMqZ7tWvTGseOHhE9VxAEnDzx\nO7Zs3iQar1CxIoCMUQe5KahZMmDgIISUKwcAePjgAV5/rbtokeubnTsxftx/C1t/PP5T45SXvHb8\n2FGzLeztyXRK1e7vvgUA+Pj44JPPPrfrdbIjyBUwOGggl8kgkUoBiRSGbIqgcrncWNR70aFDh9Ch\nQwfs27dPdC1QIOO9+umnnxoLd7Vq1YKLS8HshPeidu3aGR+fOHEiy3MFQcDQoUNx8OBBAECTJk2w\nc+dOs7WMPvnkE+Nr2717N06fPp2jfvz999/G+8eWLVtCJbLgdGHGhY2pSEtOTsbChQtFY40aNcp2\nTm94q1ZwvHoVXhcy5gGHv/kOdIGl7d5PIiIiIluM/fAj7Ni2FcnJyTh54gRqVa+KHq/1RKlSpRAV\nFYlfDx3G1atXUMrXFx07dcbG9euyzblyzVo8eHAfZ06fRmxsLAYN6IdJE79Ay1YvIzAwEFKpFLGx\nMbh+/TrOnTljXAi0X/8B2WS2n7x43fYikUiwccs2vNKqBf69fRuhT5+iY7u2qF2nLpo1bwZvbx+k\npqbizr//4sSJ3/H40SMMHDQYgwYPyZSrQ8dOxjVbXu/RHX369UOZMkGQPrth9fcPQLfu3XPcNwcH\nB6zftBmd2rVFcnIyjh87hppVK+PVLl1RoWJFJCUl4djRIzh75r+CUZeu3fDm6Lds+6IUEg1NRnw8\nN2nqtAIrZkglEkilEggyGfQ6AyQQstwFzMPDA3FxcZmKqgaDAQcPHsTBgwfh6uqKRo0aoVq1avDy\n8kJaWhoeP36Mffv2GUfsSCQSzJw5M09fW260a9cODg4OSElJweHDh7M898MPP8T27dsBAFWqVMFP\nP/2UaUSRp6cnPvjgA0yZMgUAMH78eBw5Il5INfXrr78aH3ft2jW3L6PAsYhDRdq6desszvE0nV9q\nSVK5cvht1nwEXr2Oyju3IvYDbrFJREREhU/ZkBCs37QFQwb2R1paGp4+eYLlX5lPJw8uWxY7dn6D\nH3/Ym6OcGo0GBw//hk8/+RhrV6+CTqfDnX//xZ1//7X4HE9PT/j6+dr0WnIjL163Pfn4+ODYiVN4\nY/gw/Lx/HwDg4oW/cPHCX6Lnyy2McnnrnXexY9s23LjxD8LDw7F08WKzePMWLXJVxAGAhg0b4edD\nhzGofz88uH8f8fHx2L5ta6bzJBIJho98A18uXlLktxd/rkHDRpBKpcYFfWvWqo0hQ4cVaJ/kMhkM\nBgGCVAqDYEBWe2MpFAq4uLggLi7OPIfJVuFxcXH45Zdf8Msvv4jmcHNzw4oVK9CpUyd7dN8unJyc\n0KNHD2zfvh3Xr1/HP//8g8qVK2c6b/bs2fjyyy8BZCyIfPDgQXh4eGQ6D8hY/2fp0qWIjo7G0aNH\n8fPPP6Njx45Z9mP37ox1ohQKBfr06WPjq8p/nE5FRVZ6ejrmzhVfmKxmzZqoUaNGtjmStHoIKgdE\ntWmPh3v3QzDZBYGIiIioMOnarRvO/nURw0e+gbIhIVCr1XBzc0PtOnUxdfoM/HHmHGrVrp2rnCqV\nCgsXLcaV6zfw+YSJaN6iBXz9/KBSqaBSqVDK1xcvNW2Kd8b8D7v3/oB/7z9Ek5ea5s0LtCAvXrc9\neXh44Ls9e3Hk+O8YNfotVK1aDW5ubpDJZHBxcUH16jUweOgw7Nj1LRYv/Uo0h7OzM46dPIVJU6ai\nUePG8PDwMLtht1aDBg1x6co1LFm2HO06dICfvz+USiVcXV1RpUpVvPnW2zj55xksXbbcLtcrLFxc\nXIw7sAHAvAULLO76lF8kkEAmlUIilUGWlAz1kydAFlOrxIoWtWrVwo8//ojZs2dj8ODBqF27tvHf\nikqlgr+/P9q0aYP58+fj9u3b6Nu3b16+JKu8+eabxsfPR9qY2rhxIz799FMAGYWoAwcOoHRpyzMl\nXFxc8MknnxiPP/300yx347p//z5OnToFAOjZsyc8PT1z/RoKmkTIr5XJCpF69eoBAM6fP1/APSFb\nrFu3DiNHjhSNzZ07Fw0aZL04sUEQEK6VQO1ZCu6uLvB2KxxzRYmIqGRIfXofKpkUIRUqFXRXiIiK\nlW927sSQQRmj8nu81hPbvt5ZwD3KIElNgezxIyiere2U4usLnYX1bwDgyZMnootSy2Qy1KhRo8gW\n3ho0aIBz587B398f9+/fz9fXMWHCBEyfPh0AcPbsWdSvX9+qPNevXweQMdXLGrbUJDgSh4oknU6H\n2bNni8YqVaqUozdjgtYAmYMj5EolPF04AoeIiIiIqKjT6XSYPjVjjRS1Wo0Zs8TvGQqCPCzUWMAB\nAFVkJJDFqBFLU4j0en2h2DbcWhMnTgSQUaTauTP/CmwpKSnG3a06duxodQGnoLGIQ0XSN998g9u3\nb4vGBg4caHE+rzQ9HY63b0NvEJAiUUDh5AJPJ02BD68kIiIiIiLbLV28CLduZWxHP/ajcQguW7aA\ne/QfnZ8/BJP7FKlOB+WzBcPFqNVqODo6isbCwsKynDZUmHXp0gUvvfQSAGDOnDkWd8Wzt7Vr1yIi\nIgJSqRQzZszIl2vmBd65UpFjMBgsrrIeHBxs/IEgJuC771B/1CiUmzMXzimpUCmVcHHU5FVXiYiI\niIgonxw/dhRTJmWM8qhYsRI++viTbJ6RvwSlCjpvH7M2ZXQ0JFqtxedYWrNFp9MhMjLSrv3LT0uW\nLIFUKsXly5dF18axt8TERGPhZuTIkahTp06eXzOvFM1JdFSi/fTTT7hy5YporH///hZH1SiioxG0\ndSskgoDgXw4g8Pfj+Hf1eug7FJ4V24mIiIiIKGdu3byJw4cPIS01FRf++gu7v/sWer0eSqUSazZs\ngFqtLuguZqIrVQry6ChIdDoAgEQQoIqMRKqfn+j5Dg4Oxm25XxQaGgovL68iOaugXr16WL9+Pe7e\nvYu0tLQ8v96dO3cwevRoAMCYMWPy/Hp5iUUcKlIEQbA49M3f3x+tW7e2+NyyGzdCnpz8Xy6lAkKj\nxnbvIxERERER5b1dO7/GjGlTzdpkMhmWr1yNBg0aFlCvsiGVQevrB+Wjh8YmRXw80t3dYbBQdPL0\n9MSjR48ytaenpyM6OtpsJ66iZMiQIfl2rZo1a6JmzZr5dr28VPRKdlSi/frrrzhz5oxorF+/fpDJ\nZKIxx7t34bdvn1lb2NiPYXAXXyyMiIiIiIgKtwt//QUAkMvlKBMUhJ69XseR30+g/8CBBdyzrOk9\nPTMVbFTh4Ra3HNdoNBZHFYWGhubbmjJUOHAkDhUplkbheHl5oV27duJPEgSUW74cEpOFv5KDyyJ+\n5Jt50UUiIiIiIsoH336/p6C7YCUJtP4BUN3519giT0mBPDEROmfnzGdLJPDw8MCTJ08yxVJTUxEb\nGwt3d/c87TEVHhyJQ0XGqVOncPToUdFYnz59oFQqRWMeZ87A49w5s7aIydMBC+cTERERERHlJYOz\nC/TOLmZtyogIi1uOOzk5Wbzfefr0KUfjlCAs4lCRYWlHKldXV3Tu3Fk0JtHpUG7FCrO22MZNkdTp\nVbv3j4iIiIiIKKe0AQEwLb3ItFooYmNFz30+GkdMcnIy4uPj7d9BKpRYxKEi4eLFi9j3wpo2z/Xq\n1QsODg6iMb+ffoLj/fvGY0EiQdT0mYBEkif9JCIiIiIiyglBpYb+hUWJlVFRkOj1oue7uLhAoVCI\nxkJDQ+3ePyqcWMShImHWrFmi7Y6OjujevbtoTJ6YiOCNG83aInr1QVqtOnbuHRERERERUe7pSvlB\nMNmcRWowQBkZKXquRCKxuPZNQkICEhMT86SPVLiwiEOF3q1bt/Dtt9+Kxnr06AEnJyfRWJmtW6GM\nizMe6xw0iJ04JU/6SERERERElFuCXA5dKV/jsdbBAekuLhbPd3V1tbgj79OnT+3ePyp8WMShQm/u\n3LkwiCzwpVKp0LNnT9HnqB8/RuDu3WZt4e/8DzpfvzzpIxERERERkTV0Xl7QOzsjuXQZJAaHIF2l\ntrhQsVQqtbg2TlxcHJKTk/Oyq1QIsIhDhdrjx4+xadMm0dirr74KNzc30VjImjWQarXG41RfP8SN\neT8PekhERERERGQDiRTpIeUBDw9IJBJAKoX4HlUZXF1dIZWK38pzbZzij0UcKtQWLlwIrUkx5jm5\nXI7evXuLPkeWlASnO3fM2sI/nwRBo8mTPhIREREREdlKAglkUikkUhkMkFgcjSOTySx+mB0dHY3U\n1NQ87CUVNBZxqNCKiorCqlWrRGNt2rSBj4+PaEzv6IjTa9fi/FtjkO7igoQatZDYu29edpWIiIiI\niMhmcpk0Y5SNVAq9eA0HAODu7p4xakcER+MUb/KC7gCRJUuXLkVSUlKmdolEgn79+mX53HjIENl/\nMKIGDEWwVAAsDDckIiIiIiIqPDJG4wiCDHqDAZK0NAhyOfDCYsZyuRxubm6IiYnJlCEqKgr+/v5Q\nKpX51WnKR7yzpUIpMTERS5YsEY01b94cZcqUsfhcnd6AFKkCCkdnOAf4Q1ehYl51k4iIiIiIyK5k\nUimkej0cw8PheO8elNHRoudZGo0jCALCwsLyuptUQFjEoUJp9erVolVlAOjfv3+Wz43XAwpHF6iV\nSrhoHPKie0RERERERHlCmpQE59s3oY6NgQSAMiYGEpF1QhUKBVwsbEceEREhurYoFX0s4lChk5aW\nhgULFojG6tevj0qVKll8brregDSZCgoHR3i5OkPCaVRERERERFSEGBzUEEzuYySCAFVEhOi5lrYb\nNxgMCA8Pz5P+UcHiHS4VOlu2bMGTJ09EYwMGDBBtL79kCcps3YqE5HSonF2gcVBBo1blZTeJiIiI\niIjsTyqDztfPrEmRkABpSkqmU5VKJZydnUXThIeHQ6/X50kXqeCwiEOFil6vx5w5c0RjVatWRa1a\ntTK1O928iYA9exCybh06jByK4N8OwdvZMa+7SkRERERElCf0Hh4wOJgvDaEKDwdEth23NBpHr9cj\nwsIIHiq6WMShQuXbb7/F7du3RWP9+/fPvHCXIKDcihWQPPth5hgehkprV0LBaVRERERERFRkSaAN\nCDRrkaemQp6QkOlMtVoNR0fxD7HDwsJgMBjypIdUMHinS4WGIAiYNWuWaCw4OBhNmjTJ1O518iTc\nL140a4uYOgOQy/Oii0RERERERPnC4OgEvaurWZsqIgIQKcpYGo2j1WoRGRmZJ/2jgsEiDhUaBw4c\nwKVLl0Rj/fv3h/SF0TUSrRYhK1eatcU0b4Xkdh3yrI9ERERE1jh+7Cg0Sjk0SjlGjRhe0N0hKpSm\nT51ifJ9s2bypoLtTKGj9AiA8m42w8ccfIatTBy5ubpg5c6bZeRqNBg4O4jvzhoaGcjROMcIiDhUa\nlkbh+Pr6onXr1pnaA/bsgebxY+OxIJUiatrMTOcRERER2aJyhXLGG8vjx44WdHeIqJj4asliTJ86\nBdOnTrF4jqBSQe/llaldIlKU8fT0FM2Rnp6OmJgY6ztKhQrnnFChcOLECfz++++isb59+0Imk5m1\nyePiELR5s1lbRP9BSK9WPc/6SEREREREZC9fLV2CB/fvAwC+mDjJ4nnaUr6QRUebtcmSkzOdp9Fo\noFKpkJaWlin29OlTeHh4ZF5jlIocjsShQsHSKBx3d3d07NgxU3vw5s1QJCYaj7VOzoj5bGKe9Y+I\niIiIiKhAyOSZthyXpqVBmppq1iaRSCyOxklNTUVsbGxe9ZDyEUfiUIG7dOkS9u/fLxp7/fXXoVQq\nzdocHjyA/969Zm3h730Avbd3nvWRiIiIyBYtWrZCcrquoLtBVKh9MXFSliNSSjKdpxcG9+qFoV26\n/NcWEYGUwEDAZHSNk5MTlEol0tPTM+UIDQ2Fm5sbR+MUcRyJQwVu9uzZou2Ojo7o2rVrpvZyq1ZB\nqtcbj1MCSiN+9Lt51j8iIiIiIqICJZFA6x9g3qTVQmJyX5RxmsTiTlVJSUlIENminIoWFnGoQN2+\nfRu7du0SjfXo0QOOjo5mbW7nz8Pr1CmztvBJUyGo1XnWRyIiIiJb5WR3KrGdecLCwjBj2lQ0ql8P\nft6e8HJzQe3q1TDuw7F48uRJrvpw7OgRjHnnbdStWQP+Pl5wc9KgXHAZ9OzeDZs2boBOl/1IocTE\nRHz3zTd49+230KxJYwT6+sBFo4avlwdqVauKN4YPw+FDv+SoP89fa+UK5QAAgiDg++++Q59ePVGl\nYnm4OzvatJh0VFQUtm7ejDeGD0Oj+vXg7+MFF40a/j5eqF+7Ft59+y2cOXM62zz3790z9rV9m4zN\nNtLS0rBm9Sq0bd0KwaUD4O7siMoVymHUiOE4e/ZMtjlNF8t+bv++n9C752uoVD4E7s6OCC4dgO5d\nX8V333yTbb5RI4ZnWnz7+rVr+GTch6hfuxYCSnlb/LeXlpaGdWvXoEe3LihfNgjuzo7Gr9GHH7yP\nixcuWLzuiKFDjNft1L5ttjsg9e75mvH8nt27ZYrnZHeq9m1aG8+5f+8eAODM6T8xauQIVK9SCZ6u\nzggJKo2unTvi0C8HMz0/NjYWSxZ9iRZNm6CMvy88XZ1Rt2YNTJ44IUcFDnu8B573//l6OKZtpv89\nf288t2nPHkgaNICkQQN8vm0b4oKCYXhh7VAAcHFxgVwux61bt7BgwQL07dsXrVu3RtOmTVGxYkV0\n7NgRK1asQOoL07FedO/ePUgkEkgkErRq1QpAxvt0+/btaN++PQICAqBSqeDn54cePXrgl19y9t4n\n23A6FRWoefPmif6wV6lU6Nmzp3mjXo/yy5ebNcXVrY+k7q/lZReJiIiICsTRI79h6KCBCA8PN2u/\nefMGbt68gS2bNuL7H35Ek5eaZpknPDwcI4YOxq+HD2eKPX3yBE+fPMHP+/fhy/nzsfPb71CpcmXR\nPFevXEGLpk2QkpKSKRYfH4/4+HjcunUT27ZuQdv27bFpyza4ubnl6LXGxsZi8MD+OGynm8BfDh5A\nrx7dRQtTsbGxiI2NxbVrV7F+7RoMHDQYS5evgEqlylHux48fo3fP13Dhr/Nm7Q/u38fWLZuxfdtW\nfDjuY0yZNj1H+bRaLUa/MRI7tm8zaw8PC8MvBw7glwMHsHnzRmz/elemDzgtWbZ0CT7/dLzolBpT\nZ8+eweAB/Y3FkOfS0tKMX6OVy5dhxBujsHDRYsjl5rePi5Z+hdOn/8Sdf//F0SNHsGDeXIz7ZLzo\ntVatXIGffvwBAODr54dVa9fl6LVkZ8a0qZg1Y7rZPUVKSgpCnz7F4UOH8OFH4zBtZsb6m6f//AN9\nXu+F8LAwsxz//HMd/8y+ju++/QYHD/8Gf39/0Wvl5Xsgt/QaR0Auh16vh/yF2VF6vR6LFi3Cli1b\nMt1rhYWF4cCBAzhw4ABmz56NnTt3onHjxjm6ZnR0NPr27YtDhw6ZtYeGhmLPnj3Ys2cPxo4diwUL\nFtj02ihrLOJQgXny5Ak2btwoGuvUqVOmH3i+Bw/C6c4ds7aoGXPM5oASERERFQdXLv+Nse/9D0lJ\nSWjQsCGaN28BF1dX3L9/H99/9y1iY2MRHx+Pfn1648LfV+Du7i6a5/Hjx2jzckvjTbqTkxPatmuP\nylWqQK1W4+HDhzjw8348evgQN2/ewCutWuDkn2cQFBycKVdSUiJSUlIgkUhQu05d1KxVC/7+/tBo\nNIiLjcXFSxdx9LffoNPpcOjgQfTv8zp++vkgpNKsB/8LgoBhQwbh8C+/wNXVFR06dkKFihWRnp6O\nv/46n2mX0pyIi42DTqeDXC5H/QYNUL1GTfj4+ECtViM6Ogrnzp7FyRMnIAgCtm7J2PF09br12ebV\n6XQY0Lc3Lvx1Hl5eXni1azcEBQUhJiYaB/b/jJs3b8BgMGDenNlQKBQ5Wt9lwuefYsf2bVCpVOjU\n+VVUq14d6enp+OPUSfx+/DgA4NDBg3j9te45+np+9+23WLNqJQCgeYsWaNSoMTSOjrh//z7c3FyN\n5505cxqd27dDUlISAMDZ2RmvdumKChUrIjkpCUePHsG5s2chCALWrl6FsNBQfP3Nt2brqTg7O2Pj\nlq14pWULaLVaTJsyGS1ffhkNGzYy69PVK1fw6cfjAGRM91m3YSO8RLbNzq01q1Zi4YL5UKvV6NCx\nE6pVrw6DwYDjx47i5IkTAIAF8+ehWvUaqFO3Lrp27oSEhATUqVsPrVq1gqubG27fvo3vvtmFlJQU\n/Hv7Nt4cORw/7j8gej17vQdmzp4DAJg3Z7Zx6+/nbaZcXF0ztT0nlUgglcqgNxggCILZ92X48OHY\ns2eP8bhKlSpo0KABNBoNHj58iOPHjyMhIQEPHjzAK6+8gkOHDuGll17K8mut0+nQq1cvHDlyBL6+\nvujSpQuCgoKQkJCA/fv34/LlywCAhQsXol69eujfv3+W+ch6LOJQgVm4cKHopwMymQx9+vTJ1B7Z\ntCke3L6NwB9+gFSvR0T3nkit3yA/ukpERESUr5YuXgwnJyd8s/t7dH61i1nsi4mT0KHNK7h16ybC\nw8KwdvUq0dEPBoMBQwcNMBZwBgwchPlfLoLrCzeGWq0WE7/4DIu//BLR0dEYMWwIDh85limfi4sr\npk6fgcFDh8HHx0e033fv3MGAfn1x8cJfOHrkCL7evh39Bw7M8rU+fPAADx88QJt27bB+42a73Nz7\n+fth0dKv0LtPX4sjIS5dvIi+vXvh/r172LplM4YMG4amzZpnmffPP/6AIAjo2Kkz1m/abPa1nDl7\nLmbNmI4Z06YCAObMmomOnTujXr36WeZcungxypUvj917fkCFihXNYj/v34eB/foiJSUFR48cwbKl\nSzDmvfezzLdm1Up4eHhgx65v0LxFS9FzUlJSMGzwIGMBp2mzZti6YydKlSpldt7X27fjzTdGQKvV\n4scf9mLVyhUY/dbbZufUr98AEydPwYTPP4NOp8PQQQPx59nzcHFxAZCxK9KQgQOMU3fGfvgRXm79\nSpavIacWLpiPatWq45vd3yO4bFmz2Lw5szFpwhcAgFkzpsPF1QXp6enYuHkrevfta3bu+x+MxSut\nWiAuLg6/Hj6MM6f/RMNGmUen2Os98P7YDwEAK1csNxZxnrfl1PNpTlKpDDq9DopnNZz169cbCzhy\nuRyff/45Xn31VbPnRkdHY/r06fj999+RnJyMAQMG4MqVK1mO9Dp58iQAYPTo0Vi4cCEcHByMsVmz\nZuGDDz7A4sWLAQBTp05lEScPcU0cKhDR0dFYuXKlaKxNmzaZfoEAgM7VFWfffBeHt32L0LYdEDNp\nal53k4iIiKjArFqzLlMBBwD8/Pwwb+FC4/Fek0/cTe3Zvds4GqFb9x5Ys35DpgIOACgUCsyaMw/d\nuvcAAJw6eRInT/ye6bzKVargo48/sXjzCgBlQ0Lw7fd7jDd469etsfwCTZQrXx47v/nOLgUcAGjW\nvAVGvTk6y6kstWrXxo6d/603s37t2mzzCoKAihUrYfvOXZm+llKpFJ9PmIiBgwYDyJjSMs/CBh6m\nFAoFvvt+b6YCDgB07NQZi5Z+ZTxeMH8etFpttjk3bd1msYADANu2bsHdZyPc/QMC8N2eH0T//u7b\nvz9mzZlrPJ47e5boh7BjPxqH1q9kFGbu3b2L9959xxj7+KMPce3aVQBAvfr1MXGK/f6Gd3Fxwfc/\n/JipgAMAH477GBUqZHxNb926ifPnzmHW3HmZCjgAULVaNfzv/Q+Mx3u//170enn5HrCGQiaDRCoF\nJFIYBAE6nQ7z5883xidPniy6UYyHhwe++uorlClTBkDG2jfr12c/Eq1z585YsWKFWQEHyCgozZs3\nD6VLlwYA3LhxA1evXrXlpVEWWMShAvHVV18ZK/+mJBIJ+vXrJ/qcVJ0e6XIVUitXw5P1W6ALLJ3X\n3SQiIip0HJRyq/5TNWpoMaeqUUOr81qieGu01TklL6w18pxsbd7dDBU2NWrWQo8X1wc00aZtOzg7\nOwMArl65DP0LO9QAwOpVK4yPp82Yme013/vgv5vYfT/9mJvumvH390fT5hkjWs6dPYu0tLRsnzP2\no3GZbgzzQ+06dVCxYiUAwAmRwpWYTz//Isv1cyZOnmKcPrPvpx+NIy0sGTBoMCpWqmQxPnDQYJQv\nXwHAs3VyDopP9XmuyUsv4ZU2bbM8Z9uzKWQA8MmnnxlHzYgZ/fY7KP3sZj9jnZnM6xZJJBKsWb8R\n3t7eAICdX+/A1s2b8cPevVi7ehWAjKl8GzdvhUKhyLJvuTF0+HAElha/J5BKpWjfsYPxuJSvL0a+\nMcpirk6d/xutcunSRZv6Zc17wBoZI3Ey/lPExODUnj149OgRgIxi7zvvvGOxkJmeno7x4/8bwbdp\nk/hC0qamT7e8zpNCoTArGF3IYkFssg2nU1G+S0pKwpIlS0RjzZo1Q1BQkGgs3iCFys0FGrUKanXO\nFp4jIiIiKorat2+fZVwqlSKkXHlcungBaWlpiIuLM9tWOCUlBX/+8QcAILhsWZSvUCHba9asVdv4\n+K/z4oW05/R6Pa5fu4Z/rl9HTGwMkpOSIAiCMR4VGQUg40bx3t27FhdLfq5Dx07Z9s9aaWlpuHr1\nCm7duIm4+DikJCeb9VWryxjZ8vDBA6SmpkKdxa6nUqkUnbtkHh1lKrB0adStVw/nzp6FXq/HubNn\n0Lad5e9n126Zd2kyJZFI0LVbNyxckDHC4vQff4iO0Houu69lWloaLvz1l/G4x2uWi4VAxmvu3qMH\nlj6bKvPHyZNmBY/n/Pz8sHLNWuOuU2Pf/x+USqUx/uXipShXvnyW18qtNm3bZRkvWzbE+Lhly1aZ\nFmY2FVLuv52gwkLDLJ73nL3fA9ZSJSRA/vQJZOnpOGOyi++rr74KmUwGd3d3xMTEmPXtuWbNmkEi\nkUAQBFy8eBFJSUkWp1T5+vqidu3aWfalosloshcXZCf7YRGH8t2aNWsQFRUlGhswYIBoe5JWD0Gp\ngULtAG9X57zsHhEREVGBK23hQy1Tzs5OxsdJiYlmRZwb//xjnPZy7+5ds62scyIyIlK0PS4uDnNn\nzcS2rVtyfJMWFxebZdzFxQV+fn656l9OPH36FDOmTcW3u3YiPj4+R8+JjY2Fr6+vxXi5cuXh5ORk\nMf5c9Ro1ce7sWQDArZs3syzimBbPssr33M2bN7M8t2KlrIsF9+/dM/7bCAgMzNEUttq16xof3759\n2+J5HTt1xjtj/odlS5cgMTHR2N6nbz8MGDQo2+vkVunSZbKMO5p8r0pbGLHznOn3NSk584yB5/Li\nPWA9AYqIcEiffT9vPnhgjNSqVQtAxro4rq6uiI3N3If09HSEhITg33//hV6vx507d1CjRg3RK1n6\noN3U89GBAMy+/2RfLOJQvkpPTzebp2mqXr16qGQ6lFQQ4HHmDCIbNECCIIPa2Q0uGjUUWVTQiYiI\niIqDrEaDPGe6G82L2whHR4t/YJZTYjex9+/dQ8f2bXHv7t1c5Xq+oK0lWe3AY62LFy6gS6cOFj84\ntCQtm756eHpkGX/Oy9PT+Di76VSeJudaPMfrv3NiY7PO5+pqeWrUi8/39MzZGkSm14+Jic7y3Gkz\nZmLbls3GooFPqVJY/NWyHF0nt7J7n5i+R1S5OPfF99NzefUesJ4EWv9AqG5nFPZiTIqVpv+uPDw8\nRIs4giCYTaWLjrb8vbX1ZxLZD++GKV9t2bIFjx8/Fo29uIK599GjqDZ1KqKrVMGF/32EFL/S8HTh\nKBwiIirZUtJ1ds+ZdvqM3XNqV6yEdoX4JgbW0o98w675ijOd7r9/JxUrVsLQ4cNz9XyxwsqIYUOM\nN69lgoLw5ui30LRZM5QJCoarqyvUarXxJu6N4cOwbeuWHF0ruy2zcystLQ0D+/c1FnCqVq2GEaNG\noVHjxihdugycnZ3NbkjbvfIyTvyes/Vwckps6kp+5cvN19P0pttez1m9coVZwSAiPBznzp5B61fa\n5PpahU1evQdsYXB0hM7NDfIXijQSk38zCoUCLi4uoiPSTBfKtubfA+U/FnEo3+j1esyZM0c0Vrly\nZdSpU8d4LE1PR8jq1QAAj+vX8cpbI3Dv88lIfn9svvSViIiIqCjzMPkUXqlU5nr74hdduPAXTj3b\nYjgoOBh/nDmX5c5PcXFxNl3PFj/v3487//4LAGjQsCF++fVIlgsRx8XlbKoVAERHZT0K5bkokxEN\n7u7uWZ8bFZXtdDLT67q5ZZ0vO+7u/40miooSnzb3oufru2R3/YsXLmDiF58DgHGtFUEQMHL4MJw5\nf8Fuu48VhML8HtD5+UMWFwcPk+JrrMnUKiBjNI5YEce04Jbdv1UqHLg7FeWb3bt349atW6KxAQMG\nmFV+A777Dg6hocZjg1wOrcgCakRERESUWfnyFSCTyQAA169fy3ZKT3bOnD5tfDx4yNAsb14BGLeU\nLghnT/9pfPzm6LezLOBotVrcvpX1GjOm7tz5V3SH1Rddufy38bHY1uGmLv99KVf5KmaTLztlgoKM\nCw4/evgQkZHZF3IuXfpvp6EKFhbJTkpKwtBBA43r7XwxcZJx2/rQp0/x5sgRNvW7oBXm94CgVEHn\n7YMKJuv+XP7rL0hMRtmoVKpM6zklJiYaZ0nIZDKEhISACj8WcShfCIKAWbNmicaCgoLw0ksvGY8V\n0dEI2rrV7JzwwcOhrWDbLywiIiKiksLNzQ1169UDkDEaeruN0zpiTYpA7h5Zrwtz6eJF40iYghBj\nOrLAI+uRBT/v34+UlJQc59br9dj3Y9bbrz969Mi4u5dMJkP9Bg2zPP+HvXuzve6PP/xgfNyoSZMc\n9NQylUqFOnX/W6h4z/e7szzfYDBgz/ffG48bm/zdbuqjsR/g5s0bAICmzZrh4/GfYtnKVQgIDAQA\n/Lx/H1Ysz5u1cfJDXrwHTLdb1+v11ncOgK5UKbxk8n3de/Qo5GHmu2x5vNDv3377zThVr3r16hZ3\npqLChUUcyhe//PILLly4IBrr37+/2dzdshs3Qp6cbDzWuroidvxned5HIiIiouLkrbffNT6eNWM6\n7t65k+PnvrgGi+n0LNPtqV9kMBjw6SfjctFL+/M0uVHNqq8pKSmYPOGLXOefPXOGcbSJmGlTJhsX\nde3U+dVsp6hs27IZty2MVs+Ib8GtZ6OFfHx8stzpKqcGDBpsfDxvzmwkJCRYPHf1qpV4cP8+AMDX\nz0/0+ru//RabNqwHkDElZ/3GzZDJZPDw8MC6DRuNf+t/Pv4TXLl82eb+F4S8eA+4uPw3/SmrRYVz\nRCpD8y5dUbpUKQDAo/BwrFq7FlKTRZUdHBzg4OAAIOPf/7p164yxTp062X0tJ8obLOJQvpg5c6Zo\ne6lSpdC6dWvjsePdu/Dbt8/snPCxH8PgnrOdAIiIiIgoQ+++fdH42aiN6OhotGvTGr/9etji+amp\nqfhh7150aPsKLlwwv0lt2rSZ8fH2rVuwf99PmZ4fGxuLIQMH4OiRIwW6QGrT5s2Nj79cMB/nzp3N\ndM6TJ0/QvUtn/PPP9Vz1VSKR4J9/rmNgv76Z1hcxGAyYPXMGtmzaCCBjgeGPPvkk25zp6el4rVtX\n0ULOwQM/470x7xiPx340zjgVyhYDBg5CSLlyAICHDx7g9de6i26X/c3OnRg/7iPj8cfjPzUbPfL8\n+e++Pdp4/NXylShd5r+tv1u0bIUPx30MIOPf2NBBA3M1+qmwyIv3gOnUuONHj9rcR0mpUvjszTeN\nx+OWLMF369cDJsUZT09PxMbGYuzYsXjy5AkAwN/fHx07drS9kET5ggsbU547deoUjh8/Lhrr06cP\n5M+3DBcElFu+HBKT7eiSg8sibuSbos8lIiIiym/Tp06Bl9fyHJ3bolUrjH7r7TzukWVSqRQ7dn2L\nti+3wu3bt/D40SO82rEDqlevgabNm8PX1xcGgwHR0dG4dvUKzp45g8TERACZR+JUrVYNnTq/iv37\nfoJer0evHt3R6uWXUbduPTg5O+Pf27exf99PiImJQZUqVVGpcuVsp+nklXbtO6Bmrdr4+9JFJCUl\noVWzpujQsROqVa8OpVKJ69eu4cDP+5GcnIxWL7+M9PR044K12WnUuDH0ej1++vEH1KhSCV26dUeZ\nMmUQExONA/t/xo0b/xjPHffJeDTIZioVAIx57z0sWbQIDevVQafOr6Ja9epIT0/HH6dO4vixY8bz\nmrdogXfG/C/3XxARDg4OWL9pMzq1a4vk5GQcP3YMNatWxqtduqJCxYpISkrCsaNHcPbMfzvXdena\nDW+Ofsssj16vx7Ahg4yL4w4ZNhw9evbMdL0Jkybj6JHfcPbMGVy7dhXjPx6HxUu/sstryS958R7o\n0LETdn69AwDw9uhR+P334yhXrhzkzwplLs4uGDBoUC56KcGw997HrydP4ttff4VWp8OQ8eOxeMcO\ntGzdGk5OTrhz5w5++OEH4+grlUqFqVOnwsHBAaGhofDw8OAuVYUciziU5yythePu7o5OnToZjz3O\nnIHHubsm3JsAAFQ2SURBVHNm50RMng7Y4dMGIiIiInvIzVbULy4iWhBKlSqF3//4E/975218+80u\nCIKAK1cu48oVy1Na/AMC4C6yA9HqdevRtXMn/HU+4++1o0eO4OiRI2bn1KpdBzt27sLM6dPs+0Jy\nQSqV4utd3+DVTh1w599/YTAYsH/fT5lGTrR+5RVs2rod/fu8nuPcCoUCm7ftwOuv9cClixewfu2a\nTOdIJBKM/fAjTJoyNUc5p82YhbDQMOz8egd2f/ctdn/3baZzXmnTBtt3fmNcrNoeGjZshJ8PHcag\n/v3w4P59xMfHY/u2rZnOk0gkGD7yDXy5eEmmm/vZM2cYC2AVKlTE/IVfil5LLpdj4+ataNygHhIS\nErBm1Uq0adsOXbp2tdvryQ/2fg/0fP11rFu7Gid+/x0JCQlYvXKFWbxMUFAuiziAwdkFWxcvQakp\nk7Hiu+9gMBjw16VL+OtS5gW0S5UqhZkzZ6JmzZoAMqZYxcXFZbtoMxUsFnEoT12+fBk//ZR5qCEA\n9OrVy7hbgESvR7kV5j+0Yhu9hKRO3JGKiIiIyBaurq7YtHUbPvn0M+zYthW//34c9+7dQ0x0NORy\nOdw9PFChQgXUr98Abdq1Q/MWLc3WK3zOw8MDvx07jvXr1uKbnV/j2tWrSElJgZe3NypXrozXer2O\ngYMG22W6j62Cy5bFH2fOYeXyZdi7Zw9u3byB9PR0+JQqhRo1aqJP337o1bu3VSMOAgMDceT479iw\nfh2+3bUT/96+jdjYWPiUKoUWLVpi1FtvoWHDRjnOp1AosGHzFvTo2QubN27ApUsXEREeDjc3N9Sq\nUweDBg1Br969c93PnGjQoCEuXbmGLZs34acff8Dlv/9GVGQkHBwc4O8fgBatWmHI0GGoXadOpuf+\nceokZs+cASBjG/uNW7dmuTBu2ZAQLFryFUYMGwIAePvNN1Cvfn34+/vnyWvLC/Z+D8jlcvz080Gs\nXb0KP+zdg+vXriE2NhZak12lrCEEBWHpxx9jVI8eWLt3L347exaPIiKQkpYGDw8PVKtWDQ0bNkTn\nzp0z7d4WGhrKIk4hJxFK4OpF9Z6t1H/+2arxlHcGDBiA7du3Z2p3dHTE119/bfyEyn/PHlRcvNgY\nFyQS3Dl0FGm1Mv/CICIiKg5Sn96HSiZFSIVKBd0VIsrC/Xv3UKVieQAZU5oOHv7N5pyVK5QzLhac\nnK6zOR/RixSPH0IeGQkBQJqrK7SenoDJekaxsbEIe2H3qucqVaoEZ2fnfOpp0XT9+nUAQJUqVax6\nvi01CY7EoTxz584dfP3116Kxbt26GQs48sREBG/caBaP6NWHBRwiIiIiIiIr6Er5QaLVIsXLB1qF\nAoJeB9MlqV1cXBAVFQWdLnMRMTQ0lEWcQoy7U1GemTt3rnF7RVNKpRK9evUyHpfZuhXKuDjjsc5B\ng9iJU/Klj0RERERERMWNIJcjPTgEUkdHSKRSQCKFwWQSjlQqhbt75rWvACAuLg7Jycn51VXKJRZx\nKE88ffoUGzZsEI116tTpvx8YggCHZ1vbPRf+zv+g8/XL6y4SEREREREVaxKJBFKpFBKZDHrBfOc5\nV1dX0fWvgIzROFQ4sYhDeeLLL79Eenp6pnapVIo+ffr81yCR4PKUKTg2cy7iyldAqq8f4sa8n38d\nJSIiIiIiKsbkMmnGIt5SKUznSchkMouLGEdHRyMtLS1f+ke5wyIO2V1MTAxWvLDT1HNt2rSBr6+v\nWVuyzoDQl5rj+Dc/4d7uHyFoNPnRTSIiIiIiomJPAglkUikkUhkMggSypCTg2Ygcd3d3i7u0cTRO\n4cQiDtndsmXLkJiYKBrr16+f2bFBEJAIOVTOrnB1coShQsX86CIREREREVGJIZdJIU9Lg/Pjh9A8\negTFszVJ5XI5XF1dRZ8TGRlp83bnZH/cnYrsKjk5GYtNtgo31axZMwQHB5u1JWgNkGmcoVCq4OHi\nlA89JCIiIiLKuaDgYLtvA/7PrX/tmo8oO7LoaKgfPsDzMTfKyEhonZ0BmQweHh6IjY3N9BxBEBAW\nFobAwMB87StljSNxyK7WrVuHyMhI0Vj//v0zHjwbuqfTG5AsUUDp6AwPJ43FRbWIiIiIiIjIegZn\nZ8Dkfkuq10MZHQ0AUCgUcHFxEX1eRESE6DbkVHB410x2o9VqMX/+fNFYnTp1UKVKFQBA0NatqDJ9\nOrRPw6B0coZKqYSLxiE/u0pERERERFRiCAoldN4+Zm3KmBhInk2X8vDwEH2eXq9HREREnvePco5F\nHLKbr7/+Gg8ePBCNDRgwAEDGsL0y27ej1K+/ou2IoaixbjV85BJIOAqHiIiIiIgoz+h8fGBQKIzH\nEkGA6lmBRqVSwclJfHmL8PBwGAwG0RjlP945k10YDAbMmTNHNFaxYkXUrVsXAFB23TrIUlMBAPL0\ndATv3gWNgkszERERERER5SmpDDpfP7MmRUICpCkpACyPxtFqtRaXzKD8xyIO2cX+/ftx9epV0Vj/\n/v0hkUjgdPMmfA8eNIuFf/wpDC7iq6ETERERERGR/eg9PGBwMF/KQhUeDggCHBwc4OAgvsxFWFgY\nhGdrm1LBYhGH7GL27Nmi7YGBgWjWrBkgCCi3YgUkJm/8pHIVED90RH51kYiIiIiIqISTQOsfYNYi\nT02FPCEBAODp6Sn6rLS0NEQ/WwiZChaLOGSzEydO4OTJk6Kxvn37QiaTwevkSbhfvGgWi5g6A5Bz\nKhUREREREVF+MTg5Q+9qPhtCFREBGAzQaDRQqVSizwsNDeVonEKARRyymaVROJ6enmjbti0kWi1C\nVq40i8U0b4Xkdh3yo3tERERERERkQusXAEEiMR5LdbqM3aokEotr46SkpCA+Pj6/ukgWsIhDNrl8\n+TL27dsnGuvVqxeUSiUC9uyB5vFjY7sglSJq2sz86iIRERERERGZEFQq6L28zNqU0dGQ6HRwdnaG\nwmQXK1NPnz7Nj+5RFljEIZvMnTtXtN3R0RFdunSBPC4OQZs3m8Ui+g9CerXq+dE9IiIiIiIiEqEt\n5QtBJjMeSwwGKCMjsxyNk5iYiIRn6+dQwWARh6x279497NixQzTWvXt3ODo6InjzZigSE43tWidn\nxHw2Mb+6SERERERERGJk8kxbjku0WkAQ4OLiArmF9UtDQ0Pzo3dkAYs4ZLUFCxZAr9dnalcqlXjt\ntdfg8OAB/PfuNYuFv/cB9N7e+dVFIiIiIiIiskDn6QWDSgW9SoXE0mWQEBAIAYBUKoW7u7voc+Li\n4pCcnJy/HSUjFnHIKhEREVi3bp1orEOHDvDw8EC5VasgNSnypASURvzod/Ori0RERERERJQViQTp\nIeWQXqkydM4ugFQGw7MNqFxdXSGVipcMOBqn4LCIQ1ZZunQpUlJSMrVLpVL06dMHrn//Da9Tp8xi\n4ZOmQlCr86uLRERERERElA1BqQIkUshkUkikUuglEgiCAJlMBjc3N9HnREdHIy0tLX87SgBYxCEr\nJCQk4KuvvhKNtWrVCv7+/oivVg3/fPABUl3dAABxdesjqftr+dhLIiIiIiIiyim5VAqp9Fkh59lo\nHHd3d0hMtiI3xdE4BUN8pSKiLKxZswYxMTGisX79+gEABJkM/3TojOvtu6LmNzsh6fU6YOHNT0RE\nRDlz4vixgu5CodCsRcuC7gIVcZUrlMOD+/cBAMnpugLuDVFhIYFMKoUgyKA3GCAIAuQyGVxdXREb\nG5vp7MjISPj7+1vcjpzyBos4lCtpaWlYsGCBaKxRo0YoX748AEBnMCBFqoDGyxcREybDxVGTn90k\nIiIqtp7feJZUZYKC8vwa9+/dQ5WK5e2Wb+CgwVi9br3d8pG5Sxcv4scfMjbTaNGyJVq0bFWwHSIq\nwmRSKfQGA+QGAarwUEAmg4eHh2gRRxAEhIWFITAwMP87WoKxiEO5sm3bNjx58kQ01rdvX+PjOC2g\ncnWBSqlgAYeIiMjO8qOQURiV9AIWifv770uYOX2a8ZhFHCIbCAY4REVAER4OicEAQSKB1s0NLi4u\niI+Pz3R6REQEfH19LW5HTvbHrzTlmMFgwNy5c0VjVatWRa1atQAAaTo90uVqODo4wsfFOT+7SERE\nRGQzdw8PzJw9J8tz5s2ZbZxePnLUmwgJCbF4btVq1ezaPyKivCSPiobEYAAASAQBqogIeHh5iRZx\n9Ho9IiIi4Ofnl9/dLLFYxKEc27t3L27cuCEa69evH3yOHUN0o0aIk6mhcnOBRq2CWq3K514SERER\n2cbFxQXvj/0wy3NWrlhuLOL0ev11jv4oYv659W9Bd4GocJJIofP3g9Jk5KMiMREad3c4OTkhMTEx\n01PCw8NRqlQpi9uRk33xq0w5IggCZs+eLRoLCgpCB3d3VJsyBQ0GDkTw4cNQKJTwduUoHCIiIiIi\noqJE7+YOg8Z8SQxVeDg83N1Fz9dqtYiMjMyPrhFYxKEcOnr0KM6cOSMa69unDyqsWAEAUEdHo+G8\nmWg45TMoOC+SiIiISqgtmzdBo5RDo5Rj+tQpADLWjpg/dw5aNnsJwaUD4KRWonKFcsbnHD921Pic\nUSOGZ3uN6VOnGM/fsnmT6DmVK5QznvPcqZMnMHzIYFStVAHuzo4I9PVBu1dexto1q6HT5XynppSU\nFKxdsxp9X++FKhXLw9vdFW5OGoQElUan9m0xc/o03LQwihsA/r50CfPmzEaPbl1QpWJ5eLm5wM1J\ng+DSAWjfpjXmzJqZ5Y3h89f/5sgRxraZ06cZX6/pfy9+fcS+LpakpaVh3do16NGtC8qXDYK7syP8\nfbxQv3YtfPjB+7h44UK2OUaNGG683vFjRwEAd+/cwaefjEPdmjXg7e6KUp7uaFSvLqZMmmhxJ1hb\nHTt6BGPeeRt1a9aAv48X3Jw0KBdcBj27d8OmjRuy/f6L/Zt7cP8+pkyaiMYN6qOMvy8cVQq0b9Pa\n+Jz2bVobn3P/3j0AwJkzp/Hu/9u76/CmzjYM4HdSdxfaQrEWHTIGg8FwitsYUly34Rsb9sFgwHDX\n4Q7DdcNdhruO4mW0qaQuqSTfH21PkzZNUloa0t6/69q1I+855zkR4Dx53+cdMhhVK1WEm5ODyvdE\nWUxMDBYvXIBWzZuhtHdx2FtbwsvdFXVq1cTE8ePw8oX2HlV5uX7RJUKyh2qxYiOZDDbJybCwsFB7\nhEQigUKhKIjgijw+ZZNOcuqF4+Ligu4mJrB79Ehle3yvPgURFhEREZFBOH/uLPr06okQiURvMSgU\nCkwYPxaLFy5UediSyWS4dPEiLl28iN07d2DvgUOwtrbWeK4D+/bhx5HD1d5PcFAQgoOCcO7sWfw+\ndQqevXgFr+LFVdoM6NsHf27fpvbcIRIJQiQSXLxwAfPnzsGqNevQsVOnD7jjvLtx4zp69+guPPxn\nkMlkiIyMxOPHj7ByxXIMGPQdFixarHNx1907d2Lo4O+zDU158OA+Hjy4jy2bN+Hvo8dRrnz5fLmP\nkJAQDOjbG6dPncq2L+j9ewS9f4+jR/7GwnnzsHPPXp2vu2fXLgwd/D1iYmJ0jmXCuLFYtHCB1gf+\no0f+xg+DBiI0NFRlu1QqhVQqxb27d7B0yWKMGTceE36dlO/XL+rkVlZIsbeHsdKsVGZhYXBydcW7\nhIRs7WUyGaRSKZycnAowyqKJSRzS6s6dOzhx4oTafd2/+QY+69apbJM29UNCg0YFERoRERHRJ+/F\n8+dYtmQxoqOjUa5ceTT184OLiwtCQ0Px9MnjAotj6m+TsWjBAlhaWqJFy1aoULEiAODatas4lf5v\nvYsXLmDs6F+w/I+VOZ5n+dIlGPPLz8JDsJ2dHZo0bQYfX19YWFggLCwUd+/cwdUrV5CSkoLU1NRs\n5wgNS3swd3Z2Rq0va8O3nC/s7R2QmpqKwMBAnDl9Cm/fvEFsbCx69fDHYYejaNS4ico5mjZrBmtr\na9y+dQt7du8CADRp2hRNmjbLdr0aNb7I9et1/fo1tG7uh7i4OACAjY0N2rRtBx9fX8THxeHcubO4\neeMGFAoF1q5eBUlwMHbs3gORSKTxvKdOnsTC+fMgl8vRsFEj1Kz1JSwtLRHw7Bn27d2DxMREvP/v\nP/To1hVXbtyEiYlJrmNX9t9//6FpowZCIsra2hrN/JqjfIUKMDc3R2BgII4dPYJ3gYF49uxfNGlY\nH5evXod3yZIaz3vln3+wdfMmpKSkoPrnNdCgYQPY2zvgv//+Q4yaArgAMH/eXKxdvQpGRkZo0qwZ\nqlf/HCYmJgh49kwlcXjo4EH06NZF+Oy4uLigddt28Pb2RmRkBE4cO44nTx4jOTkZ06dNRVRUJObM\nW6D1tdD1+pQmpZgHjKKiIEr/rotTUuAgkyHUzAwymSxb++DgYDg6Omr9DlDeMIlDWs2erX52Bltb\nWwxOSoJFcLCwTW5sjPAp0wsqNCIiIqJP3s4df0IsFmP+wkX4YchQvT3gzJ45A1/Wro1tO3bBw8ND\nZd/+vXvRs3s3KBQKbNqwHv+b+Cs8PT2zneP8ubMYN2a0kMDpP3AQps+cBTs7u2xtIyIisGHdWpir\nGX7RpElTjPr5F9Rv0FBtMVS5XI4Vy5Zi3JjRkMvlGDFsKO4/eqLy2tWu8xVq1/kKWzZvEpI4X9au\no7UotS4SEhLQr3cvIYFTt149bP1zJ9zc3FTa7di+Hd8PGoDk5GQcPnQQq1b+gR8GD9F47nlzZsPV\nzQ07d+/Bl7XrqOwbPXYc/Jo0QmhoKB4/foT9e/eiS7duH3wfcrkcfXv1EBI4PXr2wryFi7K9X8nJ\nyZg08X9YvHAhpFIpBvTrg1Nnz2s898b162Bubo5NW7bp3FNq7epV8C5ZEnv2HUClypXVtgkODsbg\n7wYKCZwOHb/ByjVrYWtrK7SZMWsOFi2YjwnjxwEAli1ZgoaNGqNV6zZ5vj5lUpiaIcXFFSYhmT3u\nTKVSuLi44F1ISLb2CQkJiI6OVvvnAeUf1sQhjZ4/f47du3er3de7RQuU2blTZVtor35I9i1XEKER\nERERGYxfxozF4KHD9PoLtaeXF/Yf+itbAgcAOnbqhE7fdgaQ9uB/+NBBtef437hxwsN1/4GDsGzF\nHzk+sDk4OGDUL6OzJT4AYORPo9CwUeMcZ7MRi8UYNmIkfhgyFEBab6ZzZ89ov8l8sm3rFrx6+RIA\n4OHpib0HDqm9j27du2Pm7DnC+pxZM5GUlKTx3GKxGLv27suWwAGAcuXLY+Lk34T1gwf2f+AdpDmw\nbx8uX7oEAGjfoSPWrN+g9v0yMTHBzNlz0b5DRwDAP5cv4/Kli1rPP3/R4lwNdTM1NcW+A4c0JlBW\nLF0i1ASqWq06Nm/brpLAAQCRSISffv4Fw0eOFLZNnzYtX65PqlLc3KBQGiYoUijgmJiYYw+xoKCg\nggqtyGIShzSaNy+tq2dW5ubmGBUVBeP4eGFbsp0dIsZPKMjwiIiIiD55FhYWGPXLaH2HgZE//gR7\ne/sc93f8JvNh/N7du9n2X79+DXdu3wKQNoRq1py5+R1iNl26dhWWL13UnlTIL9u2bBaWx47/X7Yk\ngrIfhgxF8RIlAKTVAzp1Un0ZggytWrdBrVpf5rhf5X24d1fHiNVbveoPYXna9Bla24/86Sdh+e+/\nDmts61W8OPr07ZereL7p9K0wjC8n27ZtFZanTJumsc7QhF8nwzJ9FqU7t2/h0cOHeb4+ZSE2QrJ7\nMZVNptHRcLNRPxNxbGys2mnIKf9wOBXlKDg4GBs3blS77/u6dVHy5EmVbZJRYyB3cCyAyIiIiIgM\nR9169TQmAQqKX/MWGveX9fERlkPVDJU4dyazJ0yHbzrlWw2RsLAw3L93F+/evUNsTIxKTxapVCos\nBzx7li/X00Ymk+HO7dvCunJSRR2xWIwOHTti6eLFAIArly9rHNbj10Lz++Ds7AwHBwdERESofR90\nlZCQgKtXrgAASpYqpfL+5qRK1WrC8u1btzS29WveIseeVDlp0bKVxv2vX71C0Pv3ANJKN6irb6TM\n1tYWTZv54dDBAwCAf/65rLGXjbbrk3qpTk6Qh4VCnJgobHNOSECQkZHamldBQUHw0eHzRh+GSRzK\n0eLFi9UWrDISizE2NBQipR468SVLIXrg9wUZHhEREZFB8C2XPzMM5VUJb2+N+22UflmPi8v+S/rT\nJ0+E5S9q1sxzPGdOn8KsGdNx+dIlnWYKioyKzPM1dfHm9WshkeTp5QVnZ2etx1Sr9rmw/Pz5c41t\nS6T32tHE2sYGEREReerR8O/Tp8J9vH71Sqfp1JWFheY8vTsAlCuX+xIKvlqOCQjITNRV/uwzGBkZ\naT1nterVhSTOi+cBebo+5USEZA9PmL3MnNLdOCEBnra2eKumiHVUVBTi4+OFXlKUvzicitSKiorC\nihUr1O4bW7Uqit2/r7It9LffAVPTggiNiIiIyKB8Cr1wgLTh8Joo1+tRN5w+XBouLLu4uOYplunT\npqJNyxa4dPGizlM9y5R6AXxMkZERwrKTk/YEDgA4OWdOqxwRIdXQUvv7AGS+F3mZBluq9H59iLj4\nOI37bT+geK22greREZHCsu6vfWY7qTRCQ0vt16ecyW1skWqT9meZ3MgIcS6uMHVxybE3VrDS5DeU\nv9gTh9RauXIlotVkVY0AjM7yhYz88ivEtdJcCZ6IiIioqMrtkBNDkJcCzWdOn8L0aVOF83Tu0hUd\nvumESpUqwc3dHRYWFkLR1NevXqFiOf0Ny/iQ+/xUpldOSUkRln19y6Fv//65Ol5bkuZDPte5OeZj\nvPaF8btYkJI9PaEIM0O8swtSoIAoNRX29vYqwx4zSKVSeHp6wszMTA+RFm5M4lA2iYmJWLhwodp9\ns0qVgv2rV8K6QiRC+PSZwCfylxURERGRoVJ+ANWlB0aC0gQTBcHJMbO3SYjSlMO5tWLZMmF5zrz5\nGDp8RI5to6KiPvg6H8pBqcZjeLjmIUVCu7DMXi/29g75HtOHcHTKfL9MTU3zZer1j83BMfO10/21\nz2zn4GCf3yGREoWZOZI9vWAkl0OemopUuRz29vaIiIhQ+2eWRCLRafgg5Q5TkZTN5s2bIZGo/4u5\nbuXKkCtNJxf6bVfIqlYvqNCIiIiICi0rpULButRCCQwM/JjhZKM8q8/NGzc++Dw3rl8DkDasaND3\nP2hs+/jRow++zocq4e0N0/QyAe8CAxEWpj2ZcO/eHWH5UynoWrasj1BT5smTx8K03Z+ysmUzX7uH\nDx6oHdaXlfJMamV9fD9GWJSFWCyGSCSCWGwEGBnnOEwtLCwMycnJBRxd4cckDqlITU3FnDlz1O6r\nUqUKZKNG4fjq9XjXuBlSLCwROWlKAUdIREREVDi5uroJy88DNBdoTUpKwoXz5z5yRKoaNm4sLB/Y\nt/eDi+5mJBOsra2FZElO9u/bq/V8JsaZPzCqmyknt8zMzFD988xCxQf279PYXi6X48D+/cJ67a++\nynMM+cHe3h6f16gBIO112b51i54j0q5kqVIo5uEBIK0X1ulTJzW2j4mJUZnSvU6dT+O1LwpMjIwg\nEosBkTjH3mdyuRwheZhhjdRjEodU7N27Fy9evFC7z9/fH4kpckSVKIXbC5bjycVrSHEvVsAREhER\nERVOXl5ecHFxAQA8evRQ45TaK1csL/CHo5o1a6H652lJgaioKIwfO+aDzpMxzCcsLAyBb9/m2O7c\n2TP4+6/DWs9na5dZODq/epv06NVbWJ47exZiYmJybLt61Uq8ffMGAOBerBia+TXPlxjyw+Ahw4Tl\nmdN/x6uXL3U+Ni9FlfOiR4+ewvLU3yar1PbJaub0aYiLSyvAXP3zGhqnF6f8ldYTRwyRkRHExsbw\nyKFgd0hISL4kVykTkzgkUCgUmDVrltp9pUuXRs1atRAtF8HUxg5W5mYw0jJNJRERERHlTrsOHYXl\nIT98p7a3y6aNG/DrhP8VZFiCGbNmCcVh161ZjeFDh+RYt0YqlWLBvLnZhunXq/e1sDz4+0FqEyTH\njx2Ff5fOOsXk65s5bfSlCxd0GoKjTY+evVC6TBkAQODbt+j8TQe1SbPdO3di3OhfhPUx48YLRZk/\nBV26dUPtOnUApL0ffk0b48zpUzm2T0xMxKGDB9GiWRPcuXO7oMJUMWT4CDg6ptUlunXzJvr17pXt\ne6BQKLB08SIsVqrjOXHSpAKNkwBjIzFMo6Nh9+Y1PBIToW4evtTUVJ2GJJLuWNiYBCdPnsSdO3fU\n7vP390dCqgIKM0uYmFvAxc6mgKMjIiIiKvxG/fwL/ty2FfHx8bh86RKqVq6Ijt90gpubG8LDw3D6\n5Ck8evQQbu7uaNmqNTauX1eg8TVo2AgzZs3GuDGjAaQlcvbs2ommzfzgW64czM3NERoagnt37+LK\nP/8gJSUFnb5VTcb8+PPPOHhgP1JTU3Hm9GlUKueDNu3aw9vbGzHR0bh48QJuXL8OABg/YSJmTv9d\nY0xlfXzg4+OLgIBnePz4EZo2agC/5i1gZ28vtGncuAnKlS+v831aWFhg/abNaOXXDPHx8bhw/jyq\nVCyPNm3bwcfXF3FxcTh/7qwQJwC0bdce3/8wWOdrFASxWIw/d+1Bs0YN8fx5AP579w5tWrZA5cqf\noe7XX8Pd3R1yuRxSqRSPHz3EjevXhYSJvnriuLu7Y8WqNejRrQtSU1Oxd89uXLxwHq3btoO3tzci\nIyNw4thxPH6cWS9p2IgRaNmqtV7iLcpM/3sHY6UETQmxGA/VJFElEglcNExHTrnDJA4JZs+enW2b\nCIC7mxsaNGyIcIUxzG3sYGdhDmNjfnSIiIiI8lup0qWxftMW9OnZHTKZDEHv32PFsqUqbUqWKoU/\nd+7G4UMH9RLjiB9/grt7Mfz800iEh4cjKioKe/fsVttWJBLBKMu/G7/4oiaW/bESI4YOQXJyMsLC\nwrIlo0xMTDBl2u/o+E0nrUkcAJg9bx66ftsJycnJuHrlCq5euaKyf9XadblK4gBArVpf4ujJU+jV\n3R9v37xBdHQ0tm/bqvYe+w8chIWLl3wy04src3Nzw8UrVzFi6BDs2b0LCoUCDx8+wMOHD3I8xsPT\nEw56nGWrXfv22LV3H74fOABhYWEICQnBhnVrs7UzMTHB6LHjMHHSZD1ESamOTipJHHO5HM4Asva7\nSUpKglQqhbOzc4HGV1jxSZwAANevX8eZM2eybe8BYIZcjjd37sGoTgOYmJrB0dY6+wmIiIiowGTU\n36DCqV379rhx+y4WLVyAs2dOI+j9e5ibm6NkqdL4plMnDPr+B9jZ2ektiQOkDdNp2bo1tmzaiOPH\nj+HhgweQhqdNs+3k7Izy5cujfoOG6NylK7y8vLId36dvP9So8QWWLlmMC+fPIej9e1hYWKBYMQ80\natIEffv1x2dVquDN69c6xdOiZStcuHwFf6xYjmtXruDdu0DEx8fnuTdJzZq1cO/hY2zZvAl/HT6E\nB/fvIzwsDBYWFvDw8ET9hg3Rp28/VKv+ac/Wamdnh01bt2Hs+P/hz21bcfHiBbx+/RoRUimMjY3h\n4OgIHx8ffPFFTTT188PX9RvovddEy1at8fDpM2xYtxZHj/yNp0+fIkIqhbW1NYqX8EaTJk3Qf+Ag\nlClbVq9xFmVyC0ukODjCOEIqbPMEIAWQtT9OcHAwnJycPslEp6ERKfTVT06PaqRXab9165aeI/l0\ndOrUCfv2qVbetwAQIBLBM/0j8r5RUwRNnQGLXP6KQURERNklBr2BmZEYpX3KaW+c7tKF8x8xIsNR\nr34DfYdAREQARMlJMHv6BCKlYVRBAP5T07Zs2bKwVxrmaMiePHkCAKhQocIHHZ+XnAR74hCePn2K\n/UrTImb4BRASOADgfukCYk1NkXN9eCIiIvqYmLwgIqJPicLEFCkurjCRBAvb3ACEAkjK0jYoKAh2\ndnbsjZNHrCxEmDt3braupsUAjM3SLmTAd0gpXbrA4iIiIiIiIqJPW4qrK+RKs7KJkTasKqu4uDi1\nM+5R7jCJU8T9999/2LJlS7btvwOwUlpPcnBE5OisaR0iIiIiIiIq0sRGSHEvprLJCarPkxmCg4PV\nbKXcYBKniFu4cCGSk5NVtlUH0DdLu5Ax4yG3tSuosIiIiIiIiMhApDo6Qm5hobKtuJp2UVFRiI+P\nL5igCikmcYowqVSKVatWZds+H6ofjLgyPojuO6DA4iIiIiIiIiJDIkKyh+ogKmsA6iaqZ2+cvGES\npwhbsWJFtjGJ7QE0ytIudOp0wJg1sImIiIiIiEg9ubUNUu1UR294AchaxlgqlUImkxVYXIUNkzhF\nVHx8PJYsWaKyzQTA3CztIr5uiHi/FgUWFxERERERERmm5GKeUCjNPmWGtNmqspJIJAUWU2HDJE4R\ntWHDBoSGhqpsGwrAR2ldIRYjfNqMAo2LiIiIiIiIDJPCzAypzs6Z6wCM1LQLDQ3NVpuVdMMkThGU\nnJyMuXNV+9w4ApiUpV1o915IqlS5wOIiIiIiIiIiw5bs5g6FkRGSbWwhLe6N/9S0USgUCAkJKfDY\nCgMmcYqgXbt24c2bNyrbJkO16FSytQ0i/pc1rUNERERERESkgZExZOUrILlUaRjZ2MDaxlZts5CQ\nEKSmphZwcIaPSZwiRqFQYPbs2SrbigEYnKVdyMifkOriUmBxERERERERUeGgMDaBSCSCWCyGvbP6\n58rU1NRsJT5IOyZxipijR4/iwYMHKtuCADQB8Na9GAAgwbM4on8YVvDBERERERERUaFhYiSGuYUF\nLK2s1O6XSCSQy+UFHJVh47zRRcysWbPUbg8o5oF/Nu9E+PWrsC9RHApz8wKOjIiIiIiIiAoXEYyM\nxHBwdkV83Ktse5OTkyGVSuGsVAyZNGMSpwi5fPkyLl68qHZfmy7+MHd0QmzX7jCzsyngyIiIiIiI\niKgwMhaLYWFlBQczM7jJZJACUC5pHBwcDCcnJ4iUpiannHE4VRGStRZOBgdHRzRs2xGmpmZwtFHf\nzY2IiIiIiIgot0QpKbB6/w5lZDJYI60mq/K044mJiYiMjNRPcAaISZwi4uHDhzh8+LDafS2+6Qxr\nJxc42lhBJOZHgoiIiIiIiPKPcXS0sGyCtESOsuDgYCgUigKNyVDxib2ImDt3rsp6FwClAVhaWqFl\n1x4wMzWBrZWlXmIjIiIiIiKiwklhbIIUVzeVba4AzJTW4+LiEBsbW6BxGSomcYqAN2/eYPv27cJ6\ncQAbATwBsLV4CTiZWcLVlnVwiIiIiIiIKP+luLpCbmIqrIsBeGVpExQUVKAxGSomcYqABQsWICUl\nRVifCcACgCmAjv8+Qf0BPWBuZprT4UREREREREQfTiRGiofqICoHANZK69HR0YiPjy/QsAwRkziF\nXFhYGNasWSOs1wLQI0ubiB+GAKwETkRERERERB9Jqr0D5JaqJTyKZ2kTHBxccAEZKCZxCrmlS5ci\nISFBWF+YZX9s+YqI6dG7YIMiIiIiIiKiIkaEZA/VQVRWAJyU1qVSKWQyWYFGZWiYxCnEYmNjsWzZ\nMmG9M4CvsrQJ/X0mYGQEIiIiIiIioo9JbmWFFHt7lW2eUE1MsDeOZsb6DoA+nrVr10IqlQJIq/w9\nO8t+aVM/JDRoVOBxERER0YcJkHLmDgDwcbTW3ogo3XcD+mPrls0AgGMnT6F+g4b6DYgA8H0pLC6c\nP4cWzZoCAHr26o3V69ZrPSalmAeMoqIgSp9S3BSAO4D36fvDwsLg4eEBExOTjxO0gWMSp5BKSkrC\n/PnzhfWRAEop7ZcbGyN8yvQCj4uIiIjyJjwhSd8h6JWTxacxGUNERARKl/ASuv27urnh+as3MDbm\nP69Jv36fOgUAYG9vj2EjRuo5mk/LhfPncOH8eQBA23btUbVaNf0GVEQpTM2Q4uIKkxCJsM0NQCiA\nZAAKhQIhISHw9PTUV4ifNP4tU0ht374d7969AwC4AJiQZX9or35I9i1X4HERERFR3n0qiYyC9ikl\nsHZs36ZStyFEIsHRI0fQtl07PUZFBMz4fRoAoIS3N5M4WVw4f154fbxLlmQSR49S3NxgLA2HKH0W\nZSOkDat6nb4/JCQE7u7uMGLpj2xYE6cQksvlmDNnjrA+FYCt0v5kWztEjM+a1iEiIiIiXW3csAEA\nYGZmJmzbtEH7MAIiIgIgNkKyu+qU485IKwMCAKmpqQgNDS3wsAwBkziF0OHDh/HkyRMAQCUAg7Ls\nl/w8BnIHxwKPi4iIiKgwuH37Fh7cvwcA6NDxG9SuUwcAcPzYUQQFBekzNFJj9br1iE9KQXxSCuuu\nfEL4vlCqkxPk5uYAgHgAzwAoz0slkUggl8v1EdonjUmcQkahUGDmzJnC+jykdU3LEO9dCtEDvy/w\nuIiIiIgKi03pvXAAoHvPnujesxeAtF+Ot6UXaiUiIm1ESPb0QqyLKx4DiM6yNzk5GeHh4foI7JPG\nJE4hc+HCBVy7dg0A0CL9P2WhU34HTIvmOHoiIiKivEpISMCuHX8CANyLFUPjJk3xbecuwrCqzRs3\n6nSeC+fPwdLUGJamxvhuQH8AQFRUFBbOn4evv6qN4sXc4GhrjcoVymHk8GH49+lTrefMOF95nzIA\n0obY79i+He1at0SZkiVgb22JsqW80aNbV5w6eULr+Zo3bSyc883r1wCA69evYdiQwahaqSLcnBxg\naWosFNJVFhMTg8ULF6BV82Yo7V0c9taW8HJ3RZ1aNTFx/Di8fPFC7TXlcrnKdTNem5wkJyejXp3a\nQvtRP2avAfPdgP7C/gvnz6k9T3mfMkKbDKdOnkCPbl1R3qcMHG2tUa5saXTr/C2uX7+W7fjg4GD8\nPnUKatf8Ah6uznBxsEPtml9g4fx5SErSXsspPDwcWzdvxqD+/fDlFzXg4eoMW0tzeLg644tqVTFs\nyGC1183w5vXrbPG/ffNG2Kb8X/OmjXM8T0JCAlavWolOHdrDt0wpONpaw83JAdUqV8KwIYNx8+YN\nrfeiqw99X/65fAn9+/RGxXI+cLCxgpe7K/yaNMLaNauRkl5fJadrZdTDAYDvBw5Q+/rkFAuQ1gtv\n9M+j8GWNz1G8mBvsrS1RqoQXWrfww/KlSxAfH6/z/V+/dhUD+/VFeZ8ycLCxQsninvBr0gjr160V\nPjPqvoPKlN/3jPc1OTkZmzdtRLs2reBbphTsrCzUHv88IADLlixG1287oUrFCnBxsIOtpTlKeLij\n4dd1MWniBAS+favz/XwoubUNjDw8YWFpqXa/RCKBIn0WK0rDwsaFzKxZs4RlEwD/Ia1AFABE1KqN\nuFZt9BEWERERUaFwYN8+REVFAQC6+fvDyMgI9vb2aNW6Dfbv24vnzwNw6eIF1Pu6fq7O+/jRI3T5\n9ptsyY2XL17g5YsX2LRhPWbPm4/vfxis0/mioqLQq3s3nDp5UmX7+//+w/59e7F/31707N0HK1au\n0nlGrQnjxmLRwgVaH6iOHvkbPwwamK2ehVQqhVQqxb27d7B0yWKMGTceE36dpNJGLBZj3cbNqP3F\n55BKpdi6ZTOaNvNDl27d1F7rt18n4vatmwCAypU/w4xZs3W6F01SU1MxcvgwrF+7RmV74Nu3CHz7\nFocOHsDCJUuF9+LwoUMY2K8PYmJiVNrfv3cX9+/dxcED+3H4yDHY2Niovd6J48fwbccOahMQkZGR\niIyMxOPHj7B+7Rr07NUbS1f8oVKLKb8cO3oEQwf/gKD371W2JyYmIibmXzx79i/Wr12DPv36Y8my\n5QU+/bNCocCE8WOxeOFClc+gTCbDpYsXceniRezeuQN7DxyCtbV1vl47Li4Owwb/gJ3pCVxlkuBg\nSIKDcfbMGcyfNxfbd+xE7TpfaTzfr/8bjwXz56ncR4hEghCJBJcuXsTG9euwY/feXMcZ+PYt/Lt2\nEb4TOZkyeRJmz5yhdl9YWBjCwsJw/do1LF64ALPmzMXgocNyHUtuubi54+2rl9m2JyYmIjIyEg4O\nDh89BkPBJE4hcu/ePRw7dkxYPwzgNIDRAMaZmEI6YzYgEukrPCIiIiKDt3HDOmG5e49ewnKPXr2w\nf1/aQ9emDRtylcSJjo5G504d8erlS3gVL47WbdqiWLFiCA4Oxl+HD+FdYCCSkpLw04jhsLCwQO8+\nfbWec/B3g3Dq5EnY2Nigbbv2KOvjg7jYWJw+fRp379wGAGzdvAlQKLB6nfaCzPPnzcXa1atgZGSE\nJs2aoXr1z2FiYoKAZ89UHpgPHTyIHt26IDU1FQDg4uKC1m3bwdvbG5GREThx7DiePHmM5ORkTJ82\nFVFRkZgzb4HKtby8vLBi1Rp069wJADBi2BDU+vJLlCxVSqXd6VMnsWhh2rEWFhbYuGUrzNPra+TF\n5IkTsH7tGtja2qJ1m7bw8fVFQkICjh87hvv37gIARo0cgc8++wypqano0a0LUlJS8HX9+qhd5ytY\nWlri4YMHOLB/H1JTU3H92jWMHf0LVqxcpfZ6UZFRSElJgbGxMb6oWROVP6sCV1dXmJubQyoNx80b\nN3D50iUoFApsTR+ul/U9c3B0FBJY/xs3Nm2bgwNGjx2X7XpeXsWzbdu+dSu+HzRAeN/KlC2LRo2b\nwNPTEykpKXhw/z6OHT2CpKQkbNqwHpEREfhz1+4Pe4E/0NTfJmPRggWwtLREi5atUKFiRQDAtWtX\ncepEWs+yixcuYOzoX7D8j5Uqx37bpQsqVqqE06dO4vSpU2nbOnfB5zVqZLtO6dJlVNZjY2Ph16Sx\n8L0xNTVF46ZN8dlnVWBtbQ2JRIKTx48jIOAZgoOC0NKvGU6cOYuaNWupvY8pkydh/ry5wnq5cuXh\n16I5HB2dEBgYiL8OH8LNGzfQ078rRLl4dktMTESXbzvh3t07cHV1RYtWrVGyZEnExcbiypV/VM4V\nFhYGALC1tUWt2rVRoUIFODg4QiwW4/3797hw7hyePn2C5ORk/PzTj7C2sUGv3n10juVD2Njawszc\nHLLExGz7goODYW9vn6vXozATKYpg36Qa6V/WW7du6TmS/NW9e3f8+Wf27LC1rR3+OnEeLmVK6yEq\nIiIiUicx6A3MjMQo7VNO52MCpLEIT0gq0lOMO1mYwscxf39l19WL589RpVIFKBQKVKlaDVdvZP7a\nnZKSgrIlSyAkJASWlpZ4+fYdbG1tczzXhfPn0KJZUwCASCSCQqFAvwEDsWDRYpVeFjKZDKN+HIkN\n69YCAGxsbHDr7n14Fc/+IJ4x5CTjfDVr1cKfu/bAw8NDpd2G9eswfMhgoWDon7v2oH2HDtnO17xp\nY1y8cEFY9y5ZEnv2HUClypXV3lNwcDBqVP0MERERANKKPq9cs1bldVAoFFi0YD4mjM9MLuzZfwCt\nWmfvLT5i2FCsXZ2W+KhZqxZOn7sg9BoKDQ1FrRrVIQkOBgAsXrYcg75TX/fxuwH9heTHsZOn1BbR\nLe9TBm/fvBHW6zdogC3bd8DFxUUl9pHDhwkxfVW3LgIDAxETHY3tO3ehYSPVYUoXzp9Dm5YtkJKS\nArFYjH9fvIKnpyeyunTxAh4/fowuXbvB3t5e7T3cu3sX3bp8KwyJOXnmLOrW+1pt24zPQQlvbzwN\nUD9sTdmD+/fRoN5XSExMhKWlJZb/sQpdunXL9sD8+tUrdO38rVDU+4/Va9Cnbz+t58/Jh7wvX9au\njW07dmX7TO/fuxc9u3eDQqHQ+Fr/PnWKMKRq1dp1OiUm+vXuJfTAada8OVauXotixVRnVVIoFFi2\nZDHGjRkNhUKBUqVL4+6DR9l6K928eQMN69UVvnuTfpuCMePGQyzOrHISGxuL7wcOwP59e4XvMgA8\nefYc3iVLqpzvzevXqOBbVmVbz169sXDJUlhZWeV4Txs3rIezswv8mjeHaQ6lNnbv3InvBw1AYmIi\n7OzsEPDqjdoeTsp/lvXs1VunpHBOIiOk+O9t2vttCsAagDR9n6+vr8Y/UwtaxkRCFSpU+KDj85KT\nYE2cQuLly5fYuXOn2n3tevRmAoeIiIgojzZt3CA8UPXo2VNln7GxMTp3TRvyEx8fj107d+h8XoVC\ngQYNG2KZmmEyZmZmWLbiD9Rv0ABAWq2ZpUsWaT2fs7Mz9h44lO1hFwD69R+Acf+bIKzPmjFda4ym\npqbYd+BQjgkcAFixdImQwKlarTo2b9ue7aFLJBLhp59/wfCRmbVrpk+bBnVmz52HihUrAQBuXL+O\nqb9NFu7vu4H9hQRO23btc0zgfIgS3t7Yve+ASgInI/aZs+cI9/TP5csIfPsW6zZuypbAAYD6DRoK\nRa/lcjn+OnxI7fXqfV0f333/Q44JHACoWq0a/tyZ2fNl/dq1ub2tHE36dQIS03s/bNyyDV39/dX2\neChZqhT2HzosPMjPmzO7QGuVeHp5Yf+hv9R+pjt26oRO33YGkPZaHz50MF+ueevWTSGBU7NWLezZ\ndyBbAgdI+2wMH/mj8Ll+9fIldqt5Nps/Z46QwOnZuw/G/W+CSgIHAKytrbFxy1ZUqlQ5169v3Xr1\nsGrtOo0JHADo268/2rRtm2MCBwA6d+2KKdN+B5A2PHPP7l25iuVD2Nk7wMzEBB4AKgMoBSCjb11w\n+vedmMQpNObNm6d2+jVTc3P0/2GoHiIiIiIiKjxSU1OxbesWAICRkRG6dPPP1qa7UmJn04bc/Ro9\necrUHIcKiEQiTJ4yVVjfvnWr1oe7YSNGwtnZOcf9P48eIyQj7t29g4cPHmg83zedvhWGr+Rk27at\nwvKUadM01tqZ8OtkWKYXMr1z+xYePXyYrY2FhQU2bd0mDJFaMG8uzp87i+VLl+D40aMAAA9PT/yx\nek22Y/Ni5I8/5Vi/xsrKCg0aNhLWq39eAy1btc7xXMo9jO7dvZunuKpVrw5f37See5cuXczTuTK8\nef0aJ9LLMdSuUwdt2rbV2N7Dw0NIVr54/hxPHj/Olzh0MfLHnzQmujp+00lYzutrnWHVH38Iy5N+\nm6K1DtCIH0cJy3//dVhlX0xMjLBNJBJhYpZ6UMpMTExUEq26Gj9hYr4OOcp4rwHg8sX8+cxpIhKJ\n4CsSwQNpiQoRAK/0fdHR0YiLi/voMRgC1sQpBCQSCdavT/uHgjkA5VGErb7thmJqstVEREREpLvj\nx44KBV+b+vnBzc0tW5vq1T9HpUqV8ejRQ9y6eRMPHzxA5c8+03puVzc3rYVQ63xVF65ubgiRSBAe\nHo6AZ8/gWy7noXjt2nfQeD4LCws082uOvXvSendcvXpFY6wtWrbSeL7Xr14Jr4+trS2aNG2msb2t\nrS2aNvPDoYMHAAD//HNZbS+fSpUrY+acufhpxHDI5XL06dUTUZGRANKLIG/YCEdHR43Xyq2mzfw0\n7i9VOrM2T5OmTTW2LV06sze8RIeeBDKZDI8ePUTAv88QFR2FhPh4lYRdckoygLQCtomJiXmuAXTu\n3Fnh/NruO0OVqlWF5du3bqFipUp5ikFXfs2zzrurqqyPj7AcGhKSL9c8d/YMgLSeaOqGe2Xl4eEB\nFxcXhIaG4vZt1WEyt27eEIpXV6laDSW8vTWeq2Xr1jAyMhLqFGljYWGhkmDUVVRUFB7cv4dXr14h\nNiYGMplMbbtnz/7N9bk/hMK9GPA2cwidPQBbpE0/HhwcjDJlyuRwZNHBJE4hsGTJEshkMtQDsA/A\nZACrASiMjPDdiB/1GhsRERFRYbBpwwZhuXv3njm2696zp1DvZdPGDZg7f0GObTNUqVJFpxgqV66M\nMxIJAOCZhiSOubm5xgSPcL7PPhOSOAFaHtC0nS8g4JnKeY2MjLRev1r16kIS58XzgBzbff/DYJw+\neRJ/HT6EkPT7B9J6E33IQ6s2xUuU0LjfyiqzLoi2tso1ROLjc+5FEBQUhOnTpmLPrp2Ijo7WKc7I\nyEi4u7vr1DYnD+7fF5Z/nzpF7XTxmoSFhWpvlE+0JT2Ue0/FxcXm+XoRERF4FxgIAEhKSoKdlUWu\njg/LMjtbQEDmZ7yyhmGJGSwtLVGqVGk81/DdUFa2rI9O37sMt2/fwrQpv+H0yZM5Ts2uLCoySudz\n54XCwRGJwUEwT59mHUjrjfMYae9JfiQvDR2HUxm46OhoLF++HCIACwC4AFgB4D6AEXXqwrsUa+EQ\nERER5YVEIsHRI38DSOtB0qZduxzbduveQ3iQ2rF9G5KUHkRy4ujopFMcTk6Zw6Mi02vPqGPv4JCt\nzoba8ykNt4qIiNTY1s7OTuP+SKXjlePU9fpSac73AwCLli5TeUCtXPkz/Dr5N52uk1vaHhCVh6vk\npq260gcAcPfOHdT6vBrWr12jcwIHgNpZfHJLGh6ep+MLcnhLfrzWuZHfr01GDzIAcHTSrfeYru0A\nwNZO96K/mzdtRP2v6uD40aM6JXAAIFGW98+bruReqslRSwAZf1pIlBK5RRV74hi4VatWISoqCj0B\n1FTaXhFAh85d9RQVERERUeGxfesW4UHHytoaI4dprjdobW2NqKgohIeH4/DBg+jUuXO+xJHfRWRz\ncz5dkkIZPqQmh7Zj5s+dozKs5PnzADz7998CG8rzschkMvTs3g3h6QmDihUrYcB33+HL2rVRvHgJ\n2NjYqCQv/Jo0wqV8rE2i/ADfzb+7ylApXdSuUyffYvnUKL82Li4u+OnnX/J0vg/5/n6M7+jTJ09U\nZqfza9EC/v49ULVaNbgXKwZLS0uh4LFCoYCVmeY6QB+DyMYGMWbmsFFKHHkibaaqsLAweHh4aK1P\nVJgxiWPAEhMTsWDBAlgAmJll31kXV7h176WPsIiIiIgKFeWhVEHv3wvTIut07Mb1WpM4Uqluv/gr\nt7N3cMixXWREBORyudaHOuWeBg4O9jrFkBMHx8x4wsPDdDomPCyznabrHz3yN/5YvgxA5vTpiYmJ\n6NOzBy5euWrQQyuOHjmCly/SpgGvWasWTpw+m22GMmVRUbr31NGFo1NmL7Bq1atjxI8/5ev5DZny\nayOTyfDjqJ/zdD7l76w0XKqhZaYILT3UPsSa1auQnJxWW2nYiBGYMy/nIZ9RUQUzhEqtEiWQGvAM\nGf3vTAAUA/CfQgGJRAIvLy8NBxduHE5lwLZs2YLg4GD8gsyq3QAgAxA5Y7aeoiIiIiIqPP65fClP\nBT3PnD6NwLdvNbZ5oGVmqAwPlWZw8vX1zbFdYmIiAp49y3G/cD6l6/r4aq+ho0nZsplFZR8+eKDT\ncBblGYTK+qi/n+DgYPwwaKCw/sfqNfiiZlr/80ePHmL82DEfGPGn4ca1q8Ly9z8M0ZjASU5OxvMA\n7e9rbpRTqnV05Z9/8vXchs7Z2VmY4S06OlrrDG7alC1bVlh+qGY2tqzi4+Px6tXLPF1TnetKn7kR\nIzUn7R4/0h7nx2JsaYUoc9U6RG4ATAGEhobqPAysMGISx0ClpqZi7ty5KAZgbJZ9f7q7o1yHTuoO\nIyIiIqJc2KjUC+eXMWMRn5Si0399+w8AkFabY/OmjRqvIQkOxrWrVzS2uXrlH6Gor5OTE3w0JHEA\nCAWDc5KQkICTJ44L67Vr521YTMlSpYQZUaOionD61EmN7WNiYnDq5AlhvY6a2bkUCgUG9e+L0PQC\nsV27+aN3n77YuHmrUMR21R8rsk3lbEgilOqkKPdmUufokSNISEjQes6Mqd11mdWocZPM2bVOHD+G\nYB1m0DJkykNwtL0+IpEIDRs1FtY3b9qgobV2Nb6oKbw39+/d1ZrcPfr33zrPTJUbkSqfOc01d/bv\n25fv188NcfESUK4qJkbasKrU1FSEhenW468wYhLHQO3fvx8BAQH4HYCV0vZQACnTsg6uIiIiIqLc\niomJwf69e4T1bv7ddT62m7+/sLxl8yatPVOm/jY5x/oXCoUC06b8Jqz79+ihtYbMsiWLIZXmPGRj\n4fx5QhHdKlWr6TQVujY9emTO2jX1t8kafymfOX2aUPi1+uc11E4vvmjBfJw+dQpAWpJo8bLlAIDS\nZcpg4eKlQrvB3w1CUFBQnuPXByelh+g7t2/n2C4hIQG//TpRp3NmFKHWVPw6Q7ny5dG4SRPhGj8O\nH6ZzHZb8rtFUEGyVCnRHaPh+ZBg8NLP+1ZpVq3DjxnWdr5X19bG1tUWr1m2Efb9Pm5rjscnJyZg9\nc4bO18oNR5XP3K0c2z198gTr1675KDHoyszSEuEWqr1xnJD2/CuRSPKlgLUhYhLHACkUCsyaNQvV\nAfTNsm+Zmztqt+uoh6iIiIiICpfdu3YKiYbPqlTNVRHdr+s3gGd6zYa3b97g7JnTObYViUQ4e+YM\nRgwbCplMprJPJpNh5PBhOHvmDADAysoKw4aP1HhtkUiE0NBQdOrQTm3Pis2bNmLm9N+F9XH/m6Dz\nfWkyZPgI4QHx1s2b6Ne7F2JjVad6VigUWLp4ERYvXChsmzhpUrZz3b59C79N+hVAWs+SjZu3wNY2\nc/ad7j17omu3tERZWFgYBvXva5BJhbpffy0sL5w/Dzdv3sjW5v379+jQtjWePn2iU9HojF5acXFx\nOiUdps+cLdQVOnTwAPy7dNaYFHv37h3mz52D9m1aaT33p0Z5GOL58+e0tq/zVV1827kLgLTvYvvW\nrbB39+4cP2spKSk4feokunT6BgcPHMi2/+cxY4RaVVs2bcTsmTOyJSJiY2PRr3cvPHz44IOKhGtT\nr17mZ27UyJEICQnJ1ubGjeto27olEvNhBrS8MvX0QnyWbcWRlugKz+MMYoaKhY0N0OnTp3Hr1i2c\ngWoW7hEAq4mTczV7ABERERGpt2nDemG5a7duuTpWJBKhc5cuWLRgQfq5NqBJ02Zq27Zp2w4PHtzH\nujWrceL4MbRp2w5ubm6QSCT46/AhlWEXc+YvQAlvb43XLl6iBKpX/xwHD+xHtcoV0bZde5T18UFc\nbCzOnDmD27duCm39u/dAh4758wOgu7s7Vqxagx7duiA1NRV79+zGxQvn0bptO3h7eyMyMgInjh3H\n48ePhGOGjRiBlq1aq5wnNjYWfXv2FIqv/m/ir6j1Ze1s11u8bDmuXbuK169e4czp01g4fx5G/TI6\nX+6loPg1b4EqVavh/r27iIuLQ8N6ddGiZStUqlwZpqamePL4MY4dPYL4+Hg0bNQISUlJ+OfyZY3n\nbNGyFa5eSRue17ljB3T190eJEt4Qp0/R7uHhifYdOgjtq1arhtVr12NAvz5ITk7GoYMHcPzYUdRv\n2BBVq1SFrZ0d4uLi8P79e9y9cwcPH9yHQqFAxYqGNzPYV3Xrwc7ODlFRUThx7Bjat22NevW+hnX6\n8DwAaNe+Azw9PYX1lWvW4u3bN7h+7RoiIyPRq4c/Jk+aiAYNG8HLywtisRiRkRF48uQJbl6/LvSA\n8+/eI9v1a9ashVE//4J5c+cAAKZMnoQd27ejRauWcHBwRGBgIA4fOogQiQS169SBSCQSahXlV0Ln\nhyFDsXrVSsTFxeHhwweoXN4X7Tt0RKnSpZGUlITr167i/LlzUCgUGD9hokrCVx8srawRYm4Ob6WE\nkjUAB6TVzHJ2dv4oya5PGZM4Bmj27NloD6BRlu0znJ0xplMXfYREREREVKg8fvQIN66n9WIQiUTo\n0jV3SRwA6Nqtu5DEOXzoIKRSqcpQhgx2dnbYvXc/OnfqiNevXgkzMSkzNTXFzNlz0C+91o42K9es\nRUxMNM6cPo1tW7eobdO9R0+sXLM2F3ekXbv27bFr7z58P3AAwsLCEBISgg3rsl/DxMQEo8eOw8RJ\nk7PtG/XjSDx/HgAAqPf11xgzbrzaa9na2mLj5i1o2qghUlJSMGXyJDRo1Ag1anyRr/f0MYnFYuzY\ntRttWrXAyxcvIJfLceTvv3Dk779U2jVu0gSbtm5H967ap6sfPHQY/ty2Df/++xQhISFYunixyv6v\n69dXSeIAwLddusDTyxPfDxyI588DIJPJcPL4cZw8fhw5McTp3S0sLPD7zFkYMXQIFAqF2nusVKmS\nShLH0tISx0+dwfixY7B29SqkpKTg5YsXwqxi6jg5OcG9mLvafVOnz0BySjKWLFoEhUKBf/99in//\nfarS5vMaX2DrnzvRu0fmsEzzLMOKPlTxEiWw9c8d6NXdH7GxsYiNjc32Z4RIJMLwkSMxcdJkvSdx\nAMCimAciXr1ERtWo5PT/y2QyREREqP1ztTBjEsfA3Lx5E+dPncKjLNuPASg5aoxKsS4iIiIqnMIT\nkrQ3ojzZtDGzF07devXgVbx4rs9RtVo1VKhQEU+ePIZMJsOO7dswZNhwtW0rVa6Mf67dwNrVq3Bg\n/368fvUScXFx8PD0ROMmTTF02HCUr1BB52vb2dnh0N9HsX3rVuz4cxseP34MaXg4nJydUavWl+g/\ncCCa+TXP9T3pomWr1nj49Bk2rFuLo0f+xtOnTxEhlcLa2hrFS3ijSZMm6D9wEMoozdaTYc+uXdi6\neRMAwMHBAes3btbYy7zWl7Xxv4m/Yupvk5GcnIx+vXrhn+s3YG1t/VHu7WMoWaoUrly/iZUrluPg\ngQMIePYvkpKS4Ormhs8+q4Ku3fzxbZcuOvc2sLGxwfnL/+CP5ctw7OgRBDx7hujoaK2z+dT5qi7u\nPnyEg/v34+iRv3H92jWEhEgQExMDKysrFCvmgQoVK6Le11+jZavWKFW6dH7cfoEbMHAQfH19sW7N\nGty4cR2S4GDEx2cdsKPKzMwMCxYtxo8/jcKWzZtw4fw5BAQECHV17B0cUKZMGVT/vAaaNG2Kxk2a\nwtTUNMfzzZw9F+07dMTqlStx6dJFhEgksLe3R1kfH3Tp5o8+ffvBzMwM0UpTytsp1fPJq+YtWuLG\n7btYvGghTp88icDAtzA2Noa7ezF8Va8e+vTtizpf1c236+WVja0dAs3MYCuTIQRAMICMks/BwcFw\ncHAoUr1xRApDHDyaRzVq1AAA3LqVcyGnT1Xnzp3htWcPFiptSwVQ384OS+7/CwtLS32FRkRERLmQ\nGPQGZkZilPbRfWrnAGms9kZFgI+j4Tyg5+TC+XNo0SxtZqCevXpj9br1Wo7QztI07ffZEt7eeBqQ\ncy8BIvr0paSkwM3JAQkJCXBzd8ert+/0HZJeRUZIEfz2DdTN1+Xr66tSM6sgPHnyBABQIRfJdWV5\nyUmwJ44BefbsGQ7u2YNXWbavBvD54GFM4BARERVyhSF5QURE2p07e0aYUr7655/rORr9s7N3QEhw\nEFKTsvdEDQ4OLvAkjj4xiWNA5s6di2QAtQHMANALQBSAWRaWWNm9HyISkzUeT0RERJ8OU7kCCiMg\nteh1iiYAcqW3XQ5Fvn8O+LkiMlypqamYNnWKsN66bTt+pwE4OrtA8v6/bNujo6MRFxcHKysrPURV\n8JjEMRDv37/H5s2bAQDvAPQGsARAGQAN+vSDp5uzHqMjIiKi3EoRiSACIC46w/hJiXL5ho/xOeDn\niujTdPrUKTx+9BB9+vVX23skLCwMwwcPxo1r1wAArm5u6NK1K7/TABycnBAWIkGqmvpOwcHBKFOm\njB6iKnhM4hgIExMTDBs2DKtWrUJcXBwA4CaAeyYmeDR2NLzYvZqIiMigvAwTQyQSwdzYSN+hkB6Y\nGmUW6zUSi/P1cyAC+Lki+kTFREZg3OjR+O3XX/F1/fqoWqUKHB0dERcXh0ePH+PkiRPC855YLMaq\nVavgbJ9/RY0NmxFcXV0R9P69ylYLCwvY29vrJyQ9YBLHQLi4uGD+/PmYMGECli9fjsWLFyM8PBw9\ne/aET0lvfYdHREREuSRO74ohLkIzalAm5fddhPz/HPBzRfRpyvhuJiYm4uSJEzh54oTadnZ2dli/\nfj06tG9fkOF98txcXSEJDoZcLoe1tTXc3d1hZ2dXpGanYhLHwDg6OuLXX3/FqFGjsH79evj5+ek7\nJCIiIiIiItJBhw4dcPToURw/fhxXr16FRCJBSEgIUlJS4OjoiEqVKsHPzw+DBg0qUr1LdGVsbIwS\nJUrAzMwMNjY2+g5HL5jEMVBWVlYYPny4vsMgIiIiog/QsGFDKPK5UGl+n4+I8p+5uTlatGiBFi1a\n6DsUg+XsXLTrwYq1NyEiIiIiIiIiIn1jEoeIiIiIiIiIyAAwiUNEREREREREZACYxCEiIiIiIiIi\nMgBM4hARERERERER6UDfReSZxCEiIiLSA5FIBACQy+V6joSIiIh0lZHEyfh7vKAxiUNERESkB0ZG\nRgCAlJQUPUdCREREukpNTQUAiMX6SacwiUNERESkB5aWlgCAmJgYPUdCREREuoqLiwMAWFhY6OX6\nTOIQERER6YGNjQ0AIDo6Wu/j64mIiEg3sbGxAABra2u9XJ9JHCIiIiI9sLa2hlgsRmJiIoKCgpjI\nISIi+sRFRUUJPWitrKz0EoOxXq5KREREVMSJxWIUL14cb9++RVRUFGQyGWxtbWFjYwNjY2OIRCK9\nFU0kIiKitCLGCoUCiYmJiIqKQlRUFADA3d0dpqameomJSRwiIiIiPbG0tESJEiUQGBiIxMREJCYm\nIiQkRN9hERERUQ4cHR3h4OCgt+sziUNERESkR5aWlvDx8UFsbCxiYmIQHx+P1NRUDq8iIiL6BIhE\nIhgbG8PW1hZ2dnYwMzPTazxM4hARERHpmVgshq2tLWxtbfUdChEREX3CWNiYiIiIiIiIiMgAMIlD\nRERERERERGQAmMQhIiIiIiIiIjIATOIQERERERERERkAJnGIiIiIiIiIiAwAkzhERERERERERAaA\nSRwiIiIiIiIiIgPAJA4RERERERERkQFgEoeIiIiIiIiIyAAwiUNEREREREREZACYxCEiIiIiIiIi\nMgBM4hARERERERERGQAmcYiIiIiIiIiIDIBIoVAo9B1EQXN0dERiYiIqVKig71CIiIiIiIiIqAh5\n8uQJzM3NIZVKc32s8UeI55Nna2ur7xCIiIiIiIiIqAgyNzf/4LxEkeyJQ0RERERERERkaFgTh4iI\niIiIiIjIADCJQ0RERERERERkAJjEISIiIiIiIiIyAEziEBEREREREREZACZxiIiIiIiIiIgMAJM4\nREREREREREQGgEkcIiIiIiIiIiIDwCQOEREREREREZEBYBKHiIiIiIiIiMgAMIlDRERERERERGQA\nmMQhIiIiIiIiIjIATOIQERERERERERkAJnGIiIiIiIiIiAwAkzhERERERERERAaASRwiIiIiIiIi\nIgPAJA4RERFROrlcjsaNG0MkEgn/zZgxQ+fj/f39VY4dNmzYR4yWiIiIihqRQqFQ6DsIIiIiok9F\nUFAQqlatitDQUACAkZERzp07h3r16mk8bu3atRg0aJCwXrVqVVy7dg1mZmYfNV4iIiIqOpjEISIi\nIsri+PHjaNmyJTL+mVS8eHHcvXsXjo6Oats/evQItWrVQnx8PADA2toat27dgq+vb4HFTERERIUf\nh1MRERERZdG8eXOMGTNGWA8MDETfvn3Vtk1ISEDXrl2FBA4ALF++nAkcIiIiyndM4hARERGp8fvv\nv+Orr74S1g8fPoyFCxdmazdixAg8evRIWO/Tpw969+5dIDESERFR0cLhVEREREQ5CAwMRLVq1SCV\nSgEApqamuHz5Mr744gsAwI4dO+Dv7y+0L1euHG7dugUrKyu9xEtERESFG5M4RERERBocOnQI7du3\nF9ZLly6NO3fuIDQ0FNWrV0dMTAwAwNzcHFevXkXVqlX1FSoREREVchxORURERKRBu3btMHLkSGH9\n5cuX6N+/P7p27SokcABgwYIFTOAQERHRR8WeOERERERaJCUloW7durh586ba/Z06dcKePXsKOCoi\nIiIqapjEISIiItLBy5cvUb16dURHR6tsL1myJO7cuQN7e3v9BEZERERFBodTEREREemgdOnSGDJk\nSLbt69atYwKHiIiICgSTOEREREQ6CAgIwPLly7Nt37Rpkx6iISIioqKISRwiIiIiLWQyGbp166ZS\nyDjD5s2bsXnzZj1ERUREREUNkzhEREREWowePRq3b98W1ps0aQILCwthfejQoXj27Jk+QiMiIqIi\nhEkcIiIiIg0OHjyIpUuXCuulS5fGvn37sHjxYmFbbGwsunbtCplMpo8QiYiIqIhgEoeIiIgoB4GB\ngejfv7+wbmJigh07dsDW1haDBg1Cly5dhH13797FL7/8oo8wiYiIqIhgEoeIiIhIjZSUFPj7+0Mq\nlQrbZs2ahZo1awrra9asQalSpYT1ZcuW4cCBAwUZJhERERUhTOIQERERqTFp0iRcvnxZWG/dujV+\n+uknlTa2trbYsWMHTExMhG39+/dHYGBggcVJRERERYdIoVAo9B0EERER0afk1KlTaN68OeRyOQDA\n09MTd+/ehbOzs9r28+bNw+jRo4X1unXr4vz58zAyMiqQeImIiKhoYE8cIiIiIiUSiQQ9e/YUEjhG\nRkbYtm1bjgkcAPj555/RqlUrYf3y5cuYPHnyR4+ViIiIihYmcYiIiIjSKRQK9OrVCxKJRNg2adIk\nNGjQQONxIpEIGzduhIeHh7Bt5syZOH369EeLlYiIiIoeDqciIiIiSjdjxgxMmDBBWG/YsCFOnz4N\nsVi3373Onj2Lpk2bCr143N3dce/ePbi6un6UeImIiKhoYRKHiIiIiIiIiMgAcDgVEREREREREZEB\nYBKHiIiIiIiIiMgAMIlDRERERERERGQAmMQhIiIiIiIiIjIATOIQERERERERERkAJnGIiIiIiIiI\niAwAkzhERERERERERAaASRwiIiIiIiIiIgPAJA4RERERERERkQFgEoeIiIiIiIiIyAAwiUNERERE\nREREZACYxCEiIiIiIiIiMgBM4hARERERERERGQAmcYiIiIiIiIiIDACTOEREREREREREBoBJHCIi\nIiIiIiIiA8AkDhERERERERGRAWASh4iIiIiIiIjIADCJQ0RERERERERkAJjEISIiIiIiIiIyAEzi\nEBEREREREREZACZxiIiIiIiIiIgMwP8BVQe6ikbNOZcAAAAASUVORK5CYII=\n" + } + }, + "id": "e6a0f0f4-aeea-4941-b7de-e954f675eee2" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_2/notebook_2/num_methods_1.ipynb b/tutorials/module_2/notebook_2/num_methods_1.ipynb new file mode 100644 index 0000000..889014a --- /dev/null +++ b/tutorials/module_2/notebook_2/num_methods_1.ipynb @@ -0,0 +1,132 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Solving non-linear equations\n", + "\n", + "^ca27a3\n", + "\n", + "## Introduction\n", + "\n", + "## Prerequisites\n", + "\n", + "``` python\n", + "import numpy\n", + "import scipy\n", + "import sympy\n", + "```\n", + "\n", + "## fsolve from SciPy\n", + "\n", + "``` python\n", + "from scipy.optimize import fsolve\n", + "\n", + "def equations(vars):\n", + " x, y = vars\n", + " eq1 = x**2 + y**2 - 25\n", + " eq2 = x**2 - y\n", + " return [eq1, eq2]\n", + "\n", + "initial_guess = [1, 1]\n", + "solution = fsolve(equations, initial_guess)\n", + "print(\"Solution:\", solution)\n", + "```\n", + "\n", + "## root from SciPy\n", + "\n", + "``` python\n", + "from scipy.optimize import root\n", + "\n", + "def equations(vars):\n", + " x, y = vars\n", + " eq1 = x**2 + y**2 - 25\n", + " eq2 = x**2 - y\n", + " return [eq1, eq2]\n", + "\n", + "initial_guess = [1, 1]\n", + "solution = root(equations, initial_guess)\n", + "print(\"Solution:\", solution.x)\n", + "```\n", + "\n", + "## minimize from SciPy\n", + "\n", + "``` python\n", + "from scipy.optimize import minimize\n", + "\n", + "# Define the equations\n", + "def equation1(x, y):\n", + " return x**2 + y**2 - 25\n", + "\n", + "def equation2(x, y):\n", + " return x**2 - y\n", + "\n", + "# Define the objective function for optimization\n", + "def objective(xy):\n", + " x, y = xy\n", + " return equation1(x, y)**2 + equation2(x, y)**2\n", + "\n", + "# Initial guess\n", + "initial_guess = [1, 1]\n", + "\n", + "# Perform optimization\n", + "result = minimize(objective, initial_guess)\n", + "solution_optimization = result.x\n", + "\n", + "print(\"Optimization Method Solution:\", solution_optimization)\n", + "```\n", + "\n", + "## nsolve from SymPy\n", + "\n", + "``` python\n", + "from sympy import symbols, Eq, nsolve\n", + "\n", + "# Define the variables\n", + "x, y = symbols('x y')\n", + "\n", + "# Define the equations\n", + "eq1 = Eq(x**2 + y**2, 25)\n", + "eq2 = Eq(x - y, 0)\n", + "\n", + "# Initial guess for the solution\n", + "initial_guess = [1, 1]\n", + "\n", + "# Use nsolve to find the solution\n", + "solution = nsolve([eq1, eq2], [x, y], initial_guess)\n", + "print(\"Solution:\", solution)\n", + "```\n", + "\n", + "## newton_method from NumPy\n", + "\n", + "``` python\n", + "import numpy as np\n", + "\n", + "def equations(vars):\n", + " x, y = vars\n", + " eq1 = x**2 + y**2 - 25\n", + " eq2 = x**2 - y\n", + " return np.array([eq1, eq2])\n", + "\n", + "def newton_method(initial_guess, tolerance=1e-6, max_iter=100):\n", + " vars = np.array(initial_guess, dtype=float)\n", + " for _ in range(max_iter):\n", + " J = np.array([[2 * vars[0], 2 * vars[1]], [2 * vars[0], -1]])\n", + " F = equations(vars)\n", + " delta = np.linalg.solve(J, -F)\n", + " vars += delta\n", + " if np.linalg.norm(delta) < tolerance:\n", + " return vars\n", + "\n", + "initial_guess = [1, 1]\n", + "solution = newton_method(initial_guess)\n", + "print(\"Solution:\", solution)\n", + "```" + ], + "id": "2ba3c111-8a56-4d09-b043-cdd8c5528e00" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_2/notebook_2/problem_solving_strategies.ipynb b/tutorials/module_2/notebook_2/problem_solving_strategies.ipynb new file mode 100644 index 0000000..d9b4afc --- /dev/null +++ b/tutorials/module_2/notebook_2/problem_solving_strategies.ipynb @@ -0,0 +1,105 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Algorithmic thinking\n", + "\n", + "In engineering, solving a problem begins long before we start coding or\n", + "building models. Like any other engineering challenge, computational\n", + "problems must first be clearly framed and understood. In this section,\n", + "you will learn to **apply algorithmic thinking** to systematically\n", + "approach engineering problems, **translate real-world situations into\n", + "structured programming logic**, and **use computational tools to\n", + "implement, test, and refine solutions**.\n", + "\n", + "Before diving into code, it’s crucial to define the problem carefully,\n", + "frame the problem so that logically so that a computer can understand\n", + "then execute so that\n", + "\n", + "## Define the Problem\n", + "\n", + "As any other engineering problem, we need to frame it before we can\n", + "start working on it. So before jumping straight into coding or building\n", + "models, clearly define the engineering problem.\n", + "\n", + "1. List your givens, this includes any constants or equations. What\n", + " inputs do we know?\n", + "2. Find: List what you’re trying to solve for. What outputs do we need\n", + " to find?\n", + "3. Establish the assumptions based on your engineering knowledge that\n", + " you deem to be appropriate to use for the problem. This determines\n", + " what mathematical models we can apply to the problem (i.e. equations\n", + " or formulas).\n", + "4. Solution: Show the works of the problem, this will include any code\n", + " used together with documentation or any explanations of the code.\n", + "5. Comment: reflect and comment on your findings.\n", + "\n", + "## Think Algorithmically\n", + "\n", + "Since we are going to use computers to compute our calculate we first\n", + "need to break the problem into logical steps that a computer can follow.\n", + "This can be done with tools such as flowchart or psuedo-code.\n", + "\n", + "- **Define the inputs and outputs.** What variables will the program\n", + " take in, and what results will it produce?\n", + "- **Break the problem into sub-tasks.** Identify steps such as data\n", + " input, logic processing and output.\n", + "- **Outline the algorithm.** Write pseudo-code or flowcharts that\n", + " describe the computational steps.\n", + "- **Identify patterns or formulas.** Can loops, conditionals, or\n", + " equations be used to automate parts of the solution?\n", + "\n", + "### Flowchart for fixing lamp\n", + "\n", + "<figure>\n", + "<img src=\"attachment:figures/LampFlowchart.png\" alt=\"Lamp Flowchart\" />\n", + "<figcaption aria-hidden=\"true\">Lamp Flowchart</figcaption>\n", + "</figure>\n", + "\n", + "### Psuedo-Code for processing and plotting stress-strain data:\n", + "\n", + "1. Import force and displacement data from file.\n", + "2. Convert data from force and displacement to stress and strain.\n", + "3. Plot the stress-strain curve.\n", + "4. Identify the yield point or modulus.\n", + "\n", + "## Write & Execute the Code\n", + "\n", + "When writing the code it is important to ask yourself whether you’re\n", + "using the right tools, libraries or method to solve the problem. **Check\n", + "for any syntax and logic errors** then debug line-by-line using print\n", + "statements or by using a debugging tool.\n", + "\n", + "## Verify and Validate\n", + "\n", + "When writing code it is crucial to test and confirm your code. It is\n", + "therefore important to ask yourself the following questions. Does the\n", + "code do what you intended it to do? And, is the mathematical model used\n", + "in the code valid for the current problem? \\## Exercise: Rubrics Cube\n", + "problem\n", + "\n", + "## Exercise: Design a derivative finding algorithm\n", + "\n", + "Set up the problem and write pseudo-code to calculate the gradient of an\n", + "unknown function.\n", + "\n", + "1. **Given:**\n", + "2. \\*\\*Find:\n", + "3. **Assumptions:**\n", + "4. **Solution:**\n", + "5. **Comment:**" + ], + "attachments": { + "figures/LampFlowchart.png": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAUQAAAG6CAYAAABwcj+vAAAABGdBTUEAALGPC/xhBQAAACBjSFJN\nAAB6JgAAgIQAAPoAAACA6AAAdTAAAOpgAAA6mAAAF3CculE8AAAABmJLR0QA/wD/AP+gvaeTAAAA\nB3RJTUUH6AYQFhwa6iTqlQAAdOZJREFUeNrtnXd4FOXXhu/Z9N5IgNACoffeuxRpUoOigCgQsCAo\nKOj3U8EKAgqo9CLYkN4UEVSK9N5rICEhDVJIQnr2/f6YzULoJSHt3Ne1V7Kzs1POzDx73va8IAiC\nIAiCIAiCIAiCIAiCIAiCIAiCIAiCIAiCIAiC8HhoObhtR6Ak4CBhLnSkAOHANQmFUJhpDcw1PQxK\nXoX+lQCsAl4CLOXxEApLhlgZmA50ALC2tKRiqTKUKOKJs4MkiIWNpJQUwqOjOBd8mbjEG5mLzwDv\nABslQkJBFsSumqb9opRyqlLGhw9eGkS3pi1wcXCU6BZy0tLT2XrkEFOX/cym/XswZY0fAZ+b/heE\nAiWIHYHfDZpmMeEVf8a9+DKWFhYSVeEO1u3aQf/PP1LxiYka8AnwsURFKEiCWE7TtEOAy48fjOel\nds9KNIX7cuJSAM1H+KvrNxIAegFrJCpCXsLwBN+dpJRy+eClQSKGwkNRvawvSz/6TNM0TQOmAbYS\nFSEv8bjl21rA9NJeRbXl47+UYrLw0JQvUYoTlwI4FXTJFYgA9klUhPyeIfYFtLf9XsTW2lqiKDwS\n7780KPPf5yUaQkEQxE4APZq3kggKj0yd8hUpU7QYQBPAVSIi5HdB9HVzcsKnWHGJoPDIaJpG7fIV\nQa+yKSMREfKzINoBzsXcPSR6wmNT3KOI+V+JhpCfBdEGwMZK6g6Fx+eWumdpaRbyfZFZEARBBFEQ\nBEEEsZAxfeVv7Dl1QgLxkHy9/Bf2nzklgRBEEG/lm+W/UnFAn3wfmAmL5/Hv4YN57rjq+Q9kzvrV\nABiNRo4GnM8Tx/XRwrlsP3ZYnihBBPFWYhLiuRh6RSKbQ1y7fp30jAwATgVdov2YERIUQcgmLHPv\nwY7lz327iYyNobh7Ebo0aYaz/U3vxFU7/qVuhcpomsb6XTuwtrKiZ/NWeLq6cfxiAP8cPoCHszO9\nW7bFzsYGgD2nTpCekUG9ipVZt2s7YVFR1PKtQOvaddGHz96dtPR01u7cTmB4GJVKlaZz42Z3XW/X\nyWPsP3MapRR1KlSkZc06d2x3x7EjHDx3BguDgVa161KzXPksnwdHRrD1yCFiEuIo6elFxwaNcbC1\nA+DQ+bPEJ96gWfVa/L5nJwGhIfgUK85zTVuah0c62dvjZG/P2eAg5m1YS0pqKsu3/k31sr5UKeOT\nZV9bDu7DzcmZehUrm5f9dWAvVhaWtKlTz7xs35mTJKem0rJmHQBOBwWy9chBElOSqVCyNM82bIy1\npRUAYVHX+O/4Ubo3b8mq7Vuxt7XluaYt7oiV0Whk3a4dFHVzp0m1GvKkCSKI92LrkUN0Gfc2tctX\npHLpMvzw5wZGffc1e2YupGxxbwBemfgpLz/bhe1HD1PNpxz/HD7AFz8t4vMhrzHlt5+pUsaHP/ft\nZs761eyYMReAb1ctIzA8DAA3JyeMSjFm1nReavcsi9+/u9uUUooO747gyIXzdGvanO3HDrPozw1o\ntxgBGY1G+n36Ib/v2UnXJs2xMBj4eNFcWtWuy+pPv8LCYCA9IwO/8e+z9cghnmvagsSUZEbPms64\nF1/mk1f8Afjt3828/OUntKpVh+IeRZizbjVvzZjKjhlzKVvcm0Ub13Pw3BmKuLiSnpGBlYUFHx06\nQIcGjVj1ySQAXmr3LNV8ynE2+DJ/H9pPSloay7f9jYWF4Q5B/OXvTVy4EsL26XMA3bi15//ew9ba\nmqtrNmEw6AWE4V9P4pm69WlZsw5f/PwDHy2cQ6dGTSni4so3y3/FzcmZf7+ZSREXV44GnKfvhA8Y\n228gizaup1fLNncVxFHff8OKbf+wY8YcecoEEcT7seSv32lXrwFrP58CQGp6GhVe6sPXy3/h27fG\nAGBtZcW6nds5vvBXnOzt2XPqBE3eGMx3q5ezb9YirCwtWbHtH/zGv09AaAi+3iWxtrJi96nj/PK/\nT3mhbXtAr+wfM2sG77/0MpVL+9xxLJsP7mPrkUNsmfodz9RtAMBXS39k9Y6t5nWW/ruZZVu3sHXa\nLFrVqmvORpu8MZhftmxiQIdOzN2wmo17d3N43o9mYVq+9W+e/+T/6N2yDbV8KzDlt595pVNXZr09\nFoD0jAyGTP6cg+fOULa4N9aWVuw9dZJF4z5kYIfOAHy3ejkjZkzh2vVYiri48v5LL+t1iRUrc/TC\nOb5dvZxlH39x1zg/27AJA7+YQFJKCnY2Nuw6eQzfEiWIjovjaMB56lSoRHR8HEcvnGfqayM5FXSJ\nDxfMYcprb/G2Xz8AImNjqNi/D5//tIhv3ngbays9UwwIDeHKit/vauzx+U+L+GXLJrZNn42vd0l5\nyoTCW4f4MCx870OzGAJYW1pRvWw5LlwJMS/TNI1uTVvgZG8PQFWfsgD0adUWK0vLLMtCr10zfQdc\nHR3p2/oZ83b6t++EUoodx47c9Vi2HNyHh7MLbevUNy97tVO3LOv8c+gAFUuWNoshQOOq1alUqoy5\nIeHPfXtoU6deliytT6u2ONs78Peh/YDemX3niaOcuRyo/xpZWPDDuI/o06qt+Zwd7GwZ0L6TeRs1\nyvkCcOXa1UeOc7t6DUnPSDe3lv99aD8ta9ahafWabD1yyJStH8TBzpZmNWry7+GDKBRDu/Ywb8PL\n1Y1OjZqw/ah+npmZ86Bnu95VDOf/vpbJS3/iz6+mU82nnDxhgmSID+J8SDAf/zCX3SePE3I1kvSM\nDAyagWfq1c+ynperm/l/G1Nm4uXqfseyzEYGgDJFi5uLggCeLq5YWVoSFh1112MJi4qimLtHlrrA\nIi6u5npJgKCIcEp5Fb3juyWKeBIUoRfRA8NDCQwPw/fFXlnWSUpJISg8HIBFYz+k/+cfU+Xl5/H1\nLknPFq0Y9GzXLMJR1M09y7HY29jecY4Pi7uTMw2rVGPrkYO0qVOPvw8e4N0X+hMRE82m/Xt4268f\n/x4+SLt6DbG2tCIoIgw3Rycc7exuO08vthzcn2VZaa9id+xv497dbD1ykFc6daN+pSrydAkiiA8i\nNT2Nju+9ha93SdZ8NplKpcpga21Ntw9Gk5KW+sTbv104lFIYjUasLe9+qgZNu+M7GUYjqWlpt2Sw\nltxITr7rubjaOgFga21D8xq1+fTVYXes5+HsAkCFkqXYO2shZy4HsmH3ThZv+p3pK39j5YSJdDPV\nw92v8edxeLZhE/45dICY+HgOnT9Dq1p1iIiJ5n8LZpNhNPLPoQOM6vOCOYO9m/CmpaffET9rqzvj\neej8GUb2foFpK5bSu2Ubnm3YRJ4wQYrM9+PM5SAuhYXyvwGvUMu3ArbW1mQYjZy4FJAt278cEU5q\n+k0xC7kWSYbRSElPr7uu713Ek9Coq6Slp5uXnQu+TIbRaH5ftrg3AaEhGG9ZZjQaCQi9QrniJfR1\ninkTdf069SpWzvKqU76i2RUoLT0dpRSVS/sw5vmXOLbgZ1rXrsvcDWtyLN7PNmzM3tMn2LR/D1XK\n+ODp6kY1n3JYWVqyce8uTl8ONAtX2eLexCXeIPy2bPpcyGXKeZd44L7ef3EQU18fyaBnuzDwywmP\nVcwXhAIpiDHx8Xe8klJSzF1rzgZfNmd0Y2ZNB+BqbOwT7zcpNYXvV68wv/9u9XLsbGzo1KjpXdfv\n2qQZ8YmJLPhjnfl4PlkyHytLS5RpYri+bdoRcjWSRX9uMH9v7oY1hEdH4Weqr3y+bTv2nTnJsq1b\nzOtsPXKIIj06cDLwInGJNyjSvUMW8UtJSyPq+vVbnV8eCRtra2IT4olPTLznOvUrVsHRzp6vl/9C\nm9r1zVloy5q1+fynRVQvW85cHdClcTMcbO347MeFKKWf+66Tx9hycJ/5PO97Mxn07PbbkWPwcnXj\nxU8/fKyiviAUKEHMMBpxf67dHa8PF87Bp1hx/Lv24PVvJlF7SH9K9e2Gu5MzHw0cwpEL52jxlv8T\n7bt+pSrsPnWcCv17U2mAH18v+4Uvh75hLrbeTrPqtXi5Yxde+2YSvi/2wrNHRyqULI23RxFzsbll\nzTpM9H+DN6dPpsrLz1Ohf2/emTmNKa+9RfMatQDo1aIN/xvwKgM+H0+F/r2pOuh5Oo0dyag+/ajm\nUw5newemvj6SMbOmU/r556jrP5BivfTGkwmDhj7WubapXQ8NjbL9ejBixpR7iJSB9vUbsv/MqSx9\nD1vVqsueUyfo1PDmD0VRN3d++r8J/PL3Jsq80J0ar75Im1Gv80qnbrzRw++hj8vexpbfPv6cA2dP\n8/GiufKUCfmGx6mwcgViapevyOF5P949M0yIu+sXXRwczcJ05nIgYVFRVC5dxpwhnQ8JNte1BUWE\n42zvgJuTk7ku8FJ4KF6u7uZK/7T0dIKvRlDcvQh2Nja8+tWnnAq8xJ6Zej1dyNVIqpQpS4king9R\nlNfXr1iqNKW9ihFyNRJ7W1vcnZzN60THx3Es4AKaBrXLV7zr3NPXrsdy/GIAVpaWVPMpZz7+TBKS\nkjhxKYDElGS8PYpk6QoUFXedxOTkLA04KWmpXLl2lRJFPO9quRZyNdJ83Lce692uSUlPL3MH68SU\nZMKjo/B0cTO35Juz7JQUDp47Q2p6GlVK+2TJYJNSUgiLvkYpz6Lm1n6AS2GhuDs7Z4lJeHQUyamp\ndzUSfvv7b5i2YilAT2T2PaGgCmJucqsgCnkbEUSh0BSZBUEQ8iOWBelk+rR6hqja1+WqCoIggtj5\nHi3JgiAIUmQWBEEQQRQEQXg6gpgCZMswO6Hwkpxqvn+SJRpCfhbEJCA2LOqaRE94bEJvDusLlWgI\n+b3IfCk2IcFsxioIj4JSiiMXzgFkAEESESG/C+IfAGv+2yYRFB6ZQ+fPcjkyAmAXIP2khHwviMsB\n9c3yX26tCxKEh+LLn3/I/HeZREPIS1g85vcigGrXb9yoZlRGs/W+IDyIjXt38eHCOZiKyq8C6RIV\nIb8LIsABTdNe/u/4UVtf7xLU9K0g0RTuy4lLAXQZ944ylSoGASclKkJBEcRY4DDw4pr/thkAmteo\nlcW+XxAyWb1jK90+GK3iEm9owCeATMcn5Dmyw6++s6ZpvyqlnCuVKsMH/QfxXNMWuDo6SXQLOanp\nafx7+CBTl/3M5gP7AIzAh8CXYHLfFYQCJogAlYBpwLMAVhaWVCxVmhJFPHFxdJQoFzKSUlIIvXaV\n8yHBxCeZ3bxPAW8Df0mEhMJCS1NRKNSUAcircL/igRVAPwqYkYggGeKj4gCUBApjitgamAL8Ckwt\nhOefAoQBUfKICfmJnPzVvgGcLaRxLWX6GwkclNtMEPIH0iQsCIIggigIgiCCKAiCIIIoCIIggigI\ngiCCKAiCIIIoCIIggigIgiCCKAiCIIIoCIIggigIgiCCKAiCIIIoCIIggigIgiCCKAiCIIIoCIIg\ngigIgiCCKAiCIIIoCIIggigIgiCCKAiCkAeRuXIfHU+g9APW8TX99QLqPWDdaOCShFUQhPxIOSCV\n7JvM/UUJqSDkDTQJwWMxDxhSqlQpGjdu/MhfvnTpEgcOHAB93upqQIaEVBCE/EppIMXZ2dkYHR2t\nHpWOHTtmZocDJZSCIBQEZgPqo48+eiQxPHDggNI0TQEXkDpcQRAKCKU0TUtxcnIyRkVFPbQgdunS\nJTM7fEVCKAhCQeI7QH3wwQcPJYaHDh3KzA4DAWsJnyAIBYnimqYl2dvbGyMiIh4oiN27d8/MDodK\n6ARBKIhMA9TYsWPvK4ZHjhzJzA4vS3YoCEJBpZimaYn29vbG8PDwewpi7969M7PD1yRkgiAUZKYC\navTo0XcVw5MnTyqDwaCAUMBWwiUIQkGmiKZpCTY2NsaQkJA7BLFv376Z2eEICZUgCIWBSYAaOXJk\nFjE8deqUMhgMStO0cMBOwiQIQmHAQ9O0eBsbG2NwcLBZEF988cXM7PBtCZEgCIWJzwH1xhtvKKWU\nOn/+vLK0tFSapkUA9hIeQRAKE66apsVaWVkZL126pAYOHJiZHb4roREEoTAyAVCdO3fOzA6vAQ4S\nFkEQCiMumqbFcNPvcJyERBCEwsxHgNI0LRpwknAIglCYcQZigfESCkEQCjP26CNXMoBzQDMJiSAI\nhZE26MavysbGMrMOMQOYjjSsCIJQiIrI003ip7p2raKCg/9PLVvWX3l42BtNwngJaC+hEgShINMJ\nCAKUp6ejcfHi55VSX5lfEREfqQED6t46y94ywF3CJgh5D5l17/FxAyYC/gB+fjWZObMnRYrcvWS8\nYcNphg1bqUJD4zRNI0IpXgNWSxgFQQQxv9NN05ijFMWLFXNSs2b10nr0qPbAL8XGJjF27B/Mm7cX\npQBYDrwBXJWQCoIIYn6jGPo8Kr01Dfr3r8v06d1xc3s0E5tNm87h77+Cy5dj0TRilWIsMFfCKwi5\ni4WE4KHx0zQ2AvXKlXNn+fIBjB7dEjs7q0feUPnyHgwb1piMDCO7dgXZKkU3oAGwHYiTUAuCZIh5\nFR9T9tbeYNAYMqQhU6d2w9Exe6ZF+e+/QIYMWc7Zs1fRNOKU4l1gHnoDjCAIkiHmmR8Lf01jDVCl\nWrWirFs3iOHDm2BtnX1hK13alcGDG5KebmT37iAbU7bYGNgBXJfLIAiSIeY2vsB8oLWlpUGNHt1S\nmzChAzY2ljm608OHrzB48AoOH76CppGkFBOAyYBRLokgSIb4tLEE3tU0lgPla9f2Zv36V7QBA+ph\naWnI8Z0XL+7Mq682wMHBhm3bLloajao90A7YBVyTyyMIkiE+LWoCC4D6traWavz4DtqYMS2xsDDk\nysEcPx7O4MHL2b8/GE0jRSk+Bqagj4YRBEEyxBzBypQVLgVKNWvmwx9/vKr16FENgyH3fi+KFnXk\nlVca4OBgzY4dlywyMoztgeeAfUC4XDZBkAwxu2mCXldY1c7OSn38cXvt3Xdb5aoQ3o2AgCiGDFnB\n1q0BaBrpSjEV+BhIkVtYEEQQnxQ7k6CMASyefbYSc+b0pnRp1zx7wEop5s3bxzvvrFc3bqRqwAng\nVWC/3MaCIIL4uLQ0ZYUVXFxs1VdfddGGDm2IpuWPUAQGxjB06Aq2bDkPkA7MBD4AbsjtLAgiiA+L\nC/AVMBTQunatwuzZvShRwiXfnYhSih9/PMSoUetUTEySBgSYzutfuaUFQQTxQXQGZgOlvLwc1fff\n99T69KmR708qLCyON95Yw+rVJ0Af2TLPVA0QL7e2IIgg3s4dFl2zZvXCw6NgzRm/fPkxXnttlYqK\nStSAQNP5bpbbWxBEEDPx0zRmKkWR4sWd1ezZvbTnnqtaYE82MjKBMWM28OOPh8w6CbwGRMltLgiF\nVxCLA98DPTUNhg5txJQpXXFysikUF3TDhtMMH75KXblyPdOI9nVgldzqglC4BFEDBmga05TCzdfX\ng3nz+tCmjW+hu6hiRCsIhVsQy6JbdLWztDTw+utN+eKLZ3FwsC7UF3fTpnMMG7aSoKAYMaIVhIcg\nvw/dMwBDNY21QOUaNYqxbt0gBg9umK0WXfmV8uU98PcXI1pBKAwZYnl0M4aWmRZdn3zSUYTwHuzc\nGcjgwfnCiLYGcAw4C9TizuGJ36EbcbSUqyrkRIaV37AExmoaJ4GWdeqUYN++EdrEiZ1FDO9Ds2Y+\nHD48irFjW2MwaM7AHGCr6YclL1IGeFeunCCCeG9qAXuAiTY2llYTJ3Zm//4R1KlTQq7kQ2BnZ8XE\niZ05cGBkZsxaahrHgLF58F74Gvg/oOJDrOtjEs+JwPtAFbnaQkEuMtsC4zSN/1MKyxYtyjJ/fh8q\nVvSUK/iYpKVl8PXXO/jww00qLS1DQzehHQycySNF5sqmKpFU4Jlbiva3F5nbA+tMx78TqI0+MulF\nYFkun4sXUBSwljsuZ29nIAKI5AmrgPKDIDY1PRiVnZxs1KefdtRGjGiW5yy68it3MaKdCHxuusly\nWxAtgUPAcGDRXQRRAy4Ap4FutzwMS4AOQEl0A4ynhTXwEtDLJOJ2coc9VVLQx/OvBn4EkgqSINoD\nH5mKQoZOnSozZ04vSpVylcuezaSnG/n++128//5GlZSUpgFH0a3FDuWyIJ4FPjMJYlVTBnCrIHoD\nV0wi9Mst23gOWGsqbp9/SsfdC33+m3IAdi52FCnvhZOnE5a2lnKT5SAZKenEX43nWsBVEmMSMxcH\nA+Nuuy/yrSB2RK/0L+PqaqcmTeqs+fs3kiufw+QRI9rbBdHW9H4f0P82QWwM7AbaktXppyGw15Sl\n/ZPDx2sAvgTeA6jWuQYthreibBNfDJYGuameIsYMI0H7A9k5bztHVx/OLC98D4x62JJCXhNEV2AS\nJosuP7+afPddD7y8HOVqPyXuYUQ72CRIuSGImIRtM/As0AWoYxLEzHU7AX/eso1W6C3ojZ7CcU8D\nRtq72auXFgzSKrapJDdRHuDSnov8OGiRio+I00zVLa8+7K9bXqGrqSuNf9GiTqxYMYBly/qLGD5l\nNE3D378RJ06M1tq3rwBQXdPYBUwHHHLpsP5GrxOadft9jz7pVrXblldDzw8u5vBxvQyMdPR0UiO2\njBYxzEOUbVyOkf+M1lxLugG8AryZXwTRC70SfL1SePv51eTkydFa795P36/w/PlrtG8/j927gwr9\nDeXj48Zffw1l2bL+uLraGYC3TNlYm1w6pDHoJr8Db1mWgF6B/iZ6v0WA0qYi0kZydupWZzSmaAaN\nl398VStSroioUB7DxduVQT8PwcLaUqHxBfDAbim5LYh+msYpYMCtD2Bu+RXGx6ewZct5rl4VN37z\nBfKryalTY7SePauD3mDwN3r9rtNTPpSrJlF0vW35cPRW5ovoDSyXTP+/ksPHMwJFkQYvNcKnUTm5\nUfIoJWqWpNmQ5hoKJ9P9kycFsbjpl30Z4OHv34jjx0djKqLlCwICovjzz7Ps3BlIfHzWNofIyAQi\nIhIAOHAghD//PEtUlN76lZFhZOfOQP755wIJCak3U52EVC5ejEYpRWhoHH/+eZaTJyMwGnN/ZF2x\nYk6sWjWQZcv6U6SIA+gGtMfRu7ZkN6cAd/TuNLez2PRZl1uWRaH3OyxmWl4Uva4xMofD0heg7dvt\nRXXyOK1HPoOmd9Pr+6B1n3Z/AA3djGGKUjiVL69bdLVunX8supKT0+nX72c2bTpH7drehIfHExeX\nzNKlL9GunS7o7777O1ev3sDFxZYTJ8KJjEwgOTmdP/8czDvvrCcpKY2goFicnW04eHAkRYo4sHHj\nGfr2/Ylp057jyy//wdPTkbNnr9KwYSk2bx6KnZ1VnsgWW7Uqp5mMaMsAm8h+I9oMIOYen6n7fHaV\np2dvVhKoWbyqNx5lpaic13HycqZMg7IE7r3og95961ReyBDLAVuAORYWBqexY1tz/PjofCWGAD//\nfIi1a09x+PAodu16g4CAsbRp48sbb6wxr2NtbcHWrQF06lSJ48ff4cKFsVhZGejYcT4TJ3bmyJG3\nOXHiHcLC4vn11yPm7wD8/vtpAgM/4Pjxd/j7b3927QpiyZKDeeb8vbwcWbLkBTZseIUSJVyUqdrj\nJNC7ED1j5QC8a8qQ0fxTdC6R5drlpiAaAH9N4zjQtmbN4uze/SYTJ3bGNh92WB08uCFxcZ9SqZJe\nP6tpGu3aVeD8+WukpOhdnQwGDScnGwYMqKv/QjnZUKNGcSpV8qRVK/16lCjhQpkyrly+HGveDsBb\nbzU3x6VFi7LUrVuCP/44k+fi0KVLFU6eHJ3ZP7QosMJUBVIYxlMWy8w8hHySJRYzz65ZPDeLzNXR\nh901tLAwqNGjW5LfLbqMRsW6dSdZufI4QUGxxMQkEh+fglKKtDQjNqaZCry9nbPM9Wxvb4WLi22W\nbdnbW5OampFlWZUqXlne3yqaeQ0XF1vmzOlNr141Mo1o/TSN9oXAiNYGwNJGRqDkFyytzdfKNjcy\nRCt0i66DQMMmTcpw7Ng7BcKi6/PP/2bo0BW0bFmO6dOfY/Nmf8aMaXVnYO8y1trC4sH94G8V0czt\n5IWGlfvRsWNFTp0aw9ixrdE0zRW9Ffp3oFQePNxv0LvmCMJTEcTamCy6bG2trCZO7MyOHa/dkfnk\nV3755Qgvv1yfkSOb06yZD+XKuRMXl30j20JCsmaDYWHxlCjhkufjYm+vW4tt3/4alSt7AnTWNE6g\nt0jnpRFRwzVNu2ASbR+RACGnBNEO3Y/uAFC3ZctyHD36tjZ2bGssLArOmE5Ng+vXk83vT52K4Jdf\nDgNw/XrSE29/3rx9KNPMUBcvRrN372U6dKiYb+LTrJkPhw7d1Yg2z/SpUkpZAf6app03VenkmZa9\nM1tOsXX63zm+n71LdnNo+YEn2sb27//l1J8nClbROpu20xyYD1RydrZVkyd3YejQhncU//ILL730\nC1ZWWYv2Pj7uHDo0ktdea8KoUeuIjU3C0tLAxYvRLFzoxzPPzOWVV5YxdWq3J9q3k5MNjRp9h6+v\nB//8c4GKFT15+eV6+Sp+mUa0L7xQm1dfXc7hw1daahpHlWICMAW9a02u4eHhwahRo5g2bZplVFTU\nq+ijX35Btz07lxP7fL/YaNJTbvoLWFhZ4FrSDZ+GZenwfifcy3joP4I7Azi6+jCtRz6TozG4ciQY\nW5cncyfbu2Q3ldpWpuqz1UUQM0tK3GLR1aVLFWbP7qWVLOmSL4NRoUIRNm8ees+HHGDEiGY0bFiK\nQ4eu4OnpSOfOlbG3t2LfvhEEBsZQvLgTo0a1IC4uOcv3P//82TvqFefM6Y2bW9ab8n//e4bLl2M5\neDCEHj2q0a1bVeztrfJlPGvX9mbv3jczjWht09IyJqJbc+WqEa2VlRX/+9//GDVqFAsWLODLL7+0\niIiIGIjuprMS3eHndHbvt/6LjWg2tAUA6SlpXL1wla3T/2bGM1MZvet9nLye3uCfXl/3RcheQXzW\nVBwqbbLoIr9bdDk52Zg7V9+PRo1K06hR1nr5evVKUq9eSYDM0Rx3iMPtNG5897r9xo1L3/Oz/IaV\nlQVjx7amS5fK2quvLmf//uCmmsaRPGBEi6OjIyNHjmTIkCHa/PnzmTRpkhYWFuaH3qfyD5MwZpsn\npHNRZ0rWvtnO5NOoHGUa+jC54Rec3nSShgMa3160Z+/i3ZRr5otXhaLm5ee3niU9NZ0qHXRPC2VU\nHF93lJCjwbiVcqOOX31CDl8mIy2DSs/cfTaF03+dxNLakgqtK3Ej6gbH1x+ldq86XDl2hfNbz2Jp\na0m1zjUoXtX7oc/PmG7k1J8nCD1xBRQUq1qcGt1qZY4SIfJ8BJf3B1K3bwMO/rafqxci8argRd2+\nDUhLTuPAr/uIj4ijVN3SVOusexmkJaVy8LcDVOlQlZjgaM7+fQZre2sqtq1MiZols/2eeJzKPVeT\nEG4ESvv51eTcuffEr1C4L9WrF2PXrjeYNu057OysrU1isx+om9vH5uDgwMiRI7l06ZI2Z84cvL29\nNaAren34eqB+Tu27SDlPDBYGrofF3vGZMipWvv0bl3ZlNe3Zs3gXO2ZuNb9f9uYv/Dr8RxKjbxB6\n/Aqzu33Llil/sXvhznvud8fMrexZvAuAuIjrrHz7NzZ9sZFNn/9OamIqpzedZHrrKUScDX+o81BK\nseD5OawavZzk60kkxyezavQyFg9YYF4naF8gK99Zzsp3fuPirgASriWwfORSfv94LQufn0P46TCi\nA6NY3H8Be5fsBiD1Rior3/6NDR+uZe24VaTEJ3Pi92PMaDuVc/9kfyHjUTPEbprGHKUoXqyYk5o5\ns2fmoH/hCSlTxg1//0b5tnj8UDebpYGRI5vTtWsVbejQFfz7b0AtdCPX3DCivQMbGxv8/f0ZNGiQ\n9sMPP/Dpp59qISEhXU3iuAX4wCTi2UbAfxcwZhgpXu3xRr1EXbrGwd/20/vr52n0chMAjq09wo+D\nFlGze+2Huy5WugzEXI7itT/eQtM00pPT+Kjs+xxfd5Si7xZ74Daig6JJiUum/8KXKddMn8jRt0UF\nfnhxHpHnIvCqWBQLawvSU9IoVqU4LV5rrQtphpHtM7fy8k9DqN5FzwoTrsVzYv0xGg1sgoWpm17E\nmXBG/jsGC2sLjOlGpredwt9fb6Zi28q5kiEWRR+zug4oPmBAXU6eHC1imI3UqlWcOXN64+pa8Kfh\n8PX14O+//ZkzpzeOjjYW6LP+HUR3us51rK2t8ff3JyAggMWLF+Pr6wvQDt1sdjOP2Sp95VgIe37Y\nxZ4fdrFz7nbWjF3J4v7zqdimEtU6Pd6zFHQgEGVUVO9a07ysZvfaOBd1fuTOTnX86psbQi1trXAr\n7U5ceNxDfdfDx4M3N79NuWblSU9JJyk2EVsnvQ909OWsw9yrd7l5rB7limCwNFC1Y7VblnkSH5l1\nv7V61TGLo8HSQLVONQg+mP02fQ/KEDXgZU3jG6Vw9fXVzRjatPEVBROeiEwj2vbtK2j+/ivZsuV8\nNfT+q+eAk+RcS/RDp+DW1tYMHDiQF154gcWLF/Pll19y6dKldiZxfGQiz0dwbO0R83snLyee+6IX\n9fs1NNezPSrx4XEYLAzYu2e1zHsc0wnHIlnNmK1srcxdwB6myLx1+t/sXriT62GxOBZxMk+hoG4b\nWGDvfrOO3cLSAltnuyzTLVhYWdzxHdcSblmP1cuJtOQ0kq4nYeeSfUnEgwSxHDBOKd2D7s03m9K6\ntXi/CdlH2bLu/O9/z7BvXzBxcckaUMn0yjNYW1vTvn17/vvvPy5duvTY26nTux6dPur6xMdjTLv5\nW2Fpa4UyKozpRixu6SqWlpL+VGN04Jd9/Pn57wxc/CqV21XFwtqCaxevManep9my/bTkrG1v6Snp\naJqGlW32VjE9SBAD0EeejAdGv/32esv1608zb14fypVzl6dZeCLi41MYO/YPZs/ejSkR2Y4+YVNO\n2njt4hHmSQ4ODmbKlCnMnj1bpaamapqmxSiltgI9czyLNmhY2liSFJuYNdM8F4mLt961zbmYM0op\nogOj8KygjwZLup5E+Kkw3Ms8vWf04s4LeFcvYW4dBrh8IDDbtn/1QlZ7y+jAazh6OmX7ePKHqUNM\nRp/Orz5w6J9/LlCt2lQ1adJWMjKMefqB27DhNCdOhOcbgbh4MZrly4/ds5jyoM/zE3/+eZbq1acy\na9ZugFhgGPrkUH+i1yfm1OuhbtrIyEjGjRtHhQoV1IwZM0hLS7sBTFJKlUM3N34q1QoeZYtwfttZ\n0pPTUEbF9plbSYhKMI9vr9i2MrZOtvw1cSMpCSl66+47y7K1GPlQxW0vJ6KDosx1f0H7Aznwqz6/\n1/XQ60+8/WNrDhNxRn+WowKjOLL6MLV71cn283gUeT2KPovZ6JSUtE/GjfvDeu3akyxY4Jdnxym/\n9toqBg2qT/XqxfKFSGzZcp5hw1aSkTGJuw3yedDndyM93ciiRftZuvQoV65cp1gxJzp3rsybbzbL\nlRbt2Ngkxo79g3nz9mZmhcuV4g2enrnr/TORq1eZOnUq06dPV8nJyZqmaYnAd0qpSdzbnDbH6Pxx\nN34ZuoT/K/UeVjZW1PGrR60edQg7cQUAGwcb+kx/gXXvr+LDMmOxd3eg04ddSbiW8FSPs8XwVpza\neIIvan6CvasdzsVdGLjkVZYO/4n1/7eapNhEXEq4Pvb2G7/SjMUDFpCSkELC1XhK1CpJ23ey3638\nccfWVQMWAg0tLQ1q9OiWWl609SpV6nMGDarPp592zBeCOHfuXrPg3c0tJyUlncTEtDtGt9yP4cNX\n8cMPBxgypCHVqxfj4sUoZs/eQ926Jfj332FPdXjl+vWnGD58lQoNjdM0jXCleP1pZVu3kFSsWDHb\nsLCwLAuvXbvGlClTmDFjhkpKStI0TUtUSs1H7zx++3QEA4Al7d7tSMcPOj/cTmMTsbS1emCdV1py\nGhmp6dg622VZFh0YhWMRRxyKOJKWnIYx3YiNo03WfVxPwtbJFs2gMbXpRMq3rEj3ib3uup+UhBQ0\ng4a1vTXGDCMp8cnYONpmadxIjk/GwtKAld3daxhu/9yYYSQ6KBoLSwNupfXiujIqEq4l4ODugDIq\nUhNTsHWxM9936clppKWkZ8lo05JSyUg3YutkS3JcEh+WGceL8wdSu2ddrl28imYw8KiTem377l82\nfLgG9MnSvs2ODPFWTgJNgCEZGcZvJk3aar9x41kWLPCjfv2ST+WuDgm5bvYY3LcvmMTENOrU8cbd\n/e4TVCUkpBIZmUDZsm7mi6GU4tKlGDw9HXBysjEvO3w4lNjYJGrWLE6RIg5cvBiNl5cjjo76hc/I\nMHLgQAhJSWnUqVMCR0drgoJiKV7cKYvVf0BAFGfOROLkZEP9+qXuyMgSElLZvTsIg0GjSZMyDzzn\nlJR0YmKSzIIYHByLk5MNzs62mY0SVK9eDG9v3bg0MDCGOXP2MGtWL4YPvzkKonZtb1566VfOn79G\nxYo57+caEZHAm2+uZsWK45mLflSKUUB0bv8IRUVF8e233/L111+r+Ph4TdO0JGC+UupLINvqW+xc\nH27iNKu7iKaVrRVFKxfL8j6TjLQMZnWZQeUOVWk3Rv/hv7TnIhFnwmnz9r0bw28VU4OF4a7Hl9lt\n5l7c/rnB4k6h0gxaliGJdtZZ92Npa4Xl7edrZ33XrgCaQcOzfM6WRp+kRtIIzFWKLcC8Y8fC2jZp\n8h2jR7dkwoQO2OSweWaXLgupV68Ex4+Hk5SURlRUIjExSSxa1Jd+/Wrfsf6qVcd5+eXfuHHjc7Mw\npaUZ8fWdyIIFfrz6agNSUtLp2nUR27dfpEaN4kRExPPFF50YOHApS5e+xPPP1yI2Nol27eZx+nQE\nVasWJSIigY8+asfQoSvYvv01WrQoS0pKOq+8sow1a05St24JQkPjSEhIYdmy/uYpE06ejKBt2zlo\nGpQvX4SIiHi6dKly33NeuvRolgyyQ4f5dO1ahV27AomLSyE6OpGoqER+/fVFevasjpWVgYUL+9Kn\nT9YpXatWLWqqJ7uR44K4fPkxhg9fpaKjEzX0GfH80Ts55yrR0dHMmDGDb775RsXFxWlAKrBYKTUe\nCMsvdbEWVhbU79eQNeNWcnztUaztrQk+cpmaPWpTu1ddhKcniJlcRO+XNTQjwzh10qStjitXHmfB\nAj9atsy5Ljo2Npb89NNhVq0aSNeuVUhPN9Kjx2LGjNlAnz417nCreRh+/fUI//xzgd2736Rhw1LE\nxibx7LP60KPM6oCZM3dz5kwkR468TYUKRQgNjaNt2zlZ1pk0aSsbNpzm0KGRVK7shdGo8PdfyfPP\n/0xg4PvY2Vnx8cd/4e5uz969b+LsbEtQUAyNGn37SMdrbW3B7Nm7Wb/+FVq39kUpRdu2c5k0aSs9\ne1anRAkXXnnlzlFnS5YcxNPTgVq1iufY9QkNjeO111axbt0p0CeHmgeMRp9LOdfF0MfHJzMjTAVm\no1vXhefHh7jxK82o1qUGwYcuo4yKopWKUcS3YMzkYGVrTe9vnqd03TJPZX/ZZVSoTNliJWDdhQtR\ntGkzh2HDVmaZajNbKz81qFatKF276lmVpaWBN95oQmhoHIcPhz7WNteuPUnjxqVp2FAfgO/qasfo\n0S1N+9PM63TqVIkKFfSigbe3M6+91iTLOr/9dpSXXqpD5cp6em8waIwb14bIyAR27QrCaFSsX3+K\nfv1q4+ysFzvKlHHDz6/mo108g0bTpj7mrFPTNJo0KU1gYPQ9i9wjR65j0aIDLF8+wFxNkJ0opZg7\ndy+VKk1WJjG8ALRFb0VOyAsPWWpqKgkJCWnA90opX/SJ7cPzs3A4eTlT9dnqVOtco8CIIYCFtQWN\nBzV9arMbZne5NhToDvgppWbPnbvXffPm88yb14dnnimf7QefKTiZlCnjZs5OHjer8fX1yLKsbt0S\nd6zTokXZe66jlCIwMJqUlHTat5+XZblerxfN1avFSE3NoFQp1yzbKVfO45GPOfOcM3F2tiUl5c5B\nHmlpGXTsOJ/Q0Dj27n0zR4rKAQFRmMYogz7SJE+MUb49FMByU9H4ohQShZwURHPVkVJsB76/dCm6\nd/v2cxk6tBGTJ3cxZ0TZlSVm+TUxOXM/ynCjW0lPN97Runu72/fDrGM0Kho1Kk2PHtWyLB82rDE1\naxYnzTTS4PY5Vh6nf+HDzNMCsGzZMXbsuERAwDh8fNyy9WKnpxv5/vtdfPDBnyoxMVVD76I1GL3f\nX16jGhAsj77wNAURIALoA3QD5sydu7f4unWn1OzZvbTu3atlyw5CQq7fkb1lFmPvqIsw1SkmJqaa\nG1Vu/36xYk6EhcVnWXZ7x+4HraNpGmXKuOHiYnvPInBaWgYGg3ZHJhsQEJVjF6N2bW/WrRuU7WJ4\n/Hg4gwcvZ//+YDSNVMh9n8MHkB1imAJkccAW8jbpqeZrlXzfaqincCzrlaIaMDc8PF7r0WMxffv+\nxLVrN554w7t2BXHyZIT5/a+/HsHLy/GuZqwlSjibH+BMvv12Z5Z+eG3blue//y5x4YIuTElJaUyd\nuj3Ldtq2Lc/GjWcID9dFMSYmie+/35VlnU6dKrN06RGCg2PNy/7++wItWswkNjYJKysLmjXzYdmy\nY+a5nEND48zdUnJiJIrBoOHomH11hmlpGUyatJV69aar/fuDAXYpZR7mmVbAn68wgPiIOFGafEJc\nmDn5Cc1tQQS9h/8woAsQvHz5MapVm6qWLz/2RBvt3Lkyffv+hJ/fj7RpM4f58/fxySd37/LTtKkP\nNWsWp1evJaYuO9NxdbXD0fHm3MiDBzfA19eDevWm07btHKpXn8oLL9TKsp1Ro5pjZ2dF9epTaddu\nLvXrT2fw4AZZ1vn443ZUquRJ7drT8PP7kc6dF9Kly0KeeaaC2d7r44/bc/JkODVqfE23boto0uQ7\nc0Z5+1zN2cG0aTvo1WtJtmzr8OErNGr0HePG/UF6ekbm0M4W5OK0AE+ZSwChx6+I0uQTbrlW9603\nzo1ZoFyAr4ChgNa1axVmz+71yFNtNmr0LdWrF+Prr7vx+++niYlJolkznyzZ4Y4dl/D2djY3lCQl\npbFhw2muXr1BnTreNGlShm3bLlKunLu5gSM5OZ1Dh65w9WoCjRuX4fr1JCpVmszWrcNp1UrvRnTj\nRioHDoQQF5dMixZlOXIklDZt5nDu3Hvm1mejUfHPPxc4c+YqTk42NGvmQ/nyWRtNLl2K5q+/zmFh\nYaBDh4rY2Vlx9Ggobdr43nWmwitXrnP6dCTPPFMeTdPYu/cyLi62WRqXAgNjCAyMNrc8Z3L6dCSR\nkQnmc3gckpLSmDBhM1OmbCMjQwFsMv3QBRXCZ+woUHPswQ8fedSE8HSJj4zj0yofoYwqECib1wQx\nkxboU0BWcHGxVV991eWRpiHIFMQFC/yy7YAOHgxh9uw9TJnSFRcXvfFn5szdjBixhtDQDyla1JGt\nWwP47bejTJ/e3dzv8H//28S0aTuIiZnwWP0f8wM7dlxiyJDlnDt3DU3julK8h963UBXS5+z/gM8a\nDmiM34x+ojp5mHUfrGbHrK2YErGx91vXMjefMaAW8PH168ljhg1babF69QnmzOlN6dKuuXJApUq5\n8tdf52jRYia9e9cgNDSOH344wIgRzShaVDfPLFHCheXLj3HkSCidOlXmwoVr/PzzYb78slOBFMO4\nuGQ+/PAvvvtuZ6bDygaleA0IKeTP2Qw0Ru7/ea9n/RcbUbax+ITmRa4cDWHX/B0KjXgUkx+0fm4/\nwenow7g2A00vXIjyXLBgn7K3t9YaNix1X+OBa9cSqVGjGLVqeWfbwTg4WDNwYD0sLQ0EB1+nSBEH\n3n23FSNGNDOv4+FhT//+dUlLyyAk5DqlS7sxfnx7XnyxToG7mTZuPEPnzgvYvPk86G40r6PXF0pr\ngj7ULxxFz9ObTqrqXWpqtzpBC7lP7JVY5vb8XiXFJmnoo6S2Peg7eWkmeVtgnKbxgVJYNW/uw4IF\nfk/FfEDISkxMEuPG/cHcuXszFy03ieE1ic4dfAOMsnO1Vy/Nf1mr9ExliUge4OKuAH56ZZGKj4zX\n0J25Bj/M9/JSGS8d2AqsBRpevhzrPX/+PmVlZaE1aVL6rnZYQvazfPkxOnVaqHbsuKRpGuHoVlef\nAokSnbuyGbBJT05rfmjZAS3kSDCOnk64lXR77HlShMfDmGHk0p6LbPhwLb9/vJbUG6kautXXCB7S\nGDivXjFLYLSm8YlSWDduXJoFC/zMLi1C9hMeHs+bb65h5crjcNOM4V0pHj803YEpQHkAW2dbivh6\n4VzUGUtbS4lODpKRkk5cZDzXAiJJik3KXHwZvQFl6aNsK6//hFVDb4lulJeNaAtCVniLRddF9C5R\n/0hkHhkr4EX0+VbaA/YSkqdKsum+XQ38xANGpeRHQQS98/gQ01So9jVrFn+qRrQFmcDAGPz9V2Q2\nmhiB+cA7wA2JTrZQBCjOI0xqJTwWaehDhSOedEP5qZKjnKkY19bS0vDUjGgLIkop5s3bxzvvrFc3\n9HqWE+iVzvskOkJhRsuHxztU05iqFI7ly3swf77fE42+KGxcuKBbdG3dGoCmka5UnrToEoRcIT9W\nxh0EFgPlo6OTKi9ZcpDQ0DjatCkvdYv3IT3dyOTJ2+jb9ycVEBClAUfQnYh+RPcuFATJEPP58ftp\nGrOVwr1sWfccM6LN7xw7Fsbgwcs5cCAETSNZKcajt4iKEApCPs8Qb+WUKVv0iY1NqvrjjwcJCIii\ndWvfLLPfFVbS0jKYMmU7/fr9okJCrmvATqAzel9PJbe/IBSsDPFWumkac5SieLFiTmrWrF7a7Y7V\nhYndu4MYPHg5p09HomkkKcUEYDIP2UFVEEQQ8z+uwCT0qS7x86vJzJk9KVKk8IwxTUxM45NPslh0\n/Ylu0XVZbndBKFyCmEknYA5QysvLUU2e3EUbOLBegb+Y27dfZMiQFZw/n8Wia67c5oJQuAURwBl9\nDO6bgOFxjWjzA9evJ/Pee78zb95eTLMPbACGA2LpLAgiiFlogT4Co+LjGNHmdX7//TTDh68iJOQ6\nmkakUrwBrJBbWxBEEO+FHXrn4zGAxbPPVspVI9rs4B4WXa8BUXJbC8LjUVh6Mj+2EW1eZPnyYzz7\n7IJMi67LQF/06T+T5JYWBMkQHwUr4B1N49NMI9r58/2oVCnvG9GGhcXxxhtrWL36BNy06BoDxMut\nLAiSIT4ORvQOyvnGiFYpxY8/HuK5535Qhw+HakAA0Afd/DJVbmNBkAwxO8jzRrSXLkXj77+SLVvO\nZxb9ZwIfIBZdgiAZYg5li6uBeiEh10vOnbtXJSamai1blrvr3MhP7cCMukVXjx6L1dmzVzXgOLor\n8wJ0/zdBECRDzDEyjWi/VgqHGjWKsXBh31wxoj15MoLBg5ezd+/lWy26PpLisSBIhvi0UOjWYr8C\n1SMjE8otWrSfxMRUmjcvi6VlzmeLmRZdL7zws7p8OVYD9qCPuvkVcaYRBMkQczEuQzWNKUrh9DSM\naI8e1S26Dh4Uiy5BkAwx73EQ+AGTEe3ixQdyxIg2OTmdzz77mwEDflVXrlzXgB3oFl3rEIsuQZAM\nMQ/ip2nMUgqPsmXdmTu3N+3aVXjije7aFcTgwcs4c+YqmkacUnyE3pVGLLoEQQQxT1MU+A7oo2nQ\nv39dpk17Dnf3R59pMtOia/LkbRiNCuAPdDOGYAmzIIgg5ie6maYt8H4cI9pNm84xbNhKgoJi0DRi\nlWIsYtElCCKI+RhXHtGINjY2ibFj/7jVoms58AZwVcIpCEJBoBMQBChPT0fj4sXPK6W+uuO1bt0g\n5e3tbASUphEO9JLQCYJQEHEGpqN3j1Fdu1ZRISH/p5T6SoWHf6QGDKir0FuLFbAMcJeQCYJQ0GmD\nbrqg3NzsjGPHtlZubnaZQngReEZCJAhCYcIe+Aa924wy/Z0GOEhoBEEorIw1CeJvEgpByD8YJAQ5\nwlnT3zAJhSCIIAqCIIggCoIgiCAKT0Ip9E7e5e/xeRHT5zUkVIIg5Dd6oDeqTHvI9S2BA8A+7u5A\n9BMQCXhKaAVBKOiCCFAL3RH7rduWdzRtq7eEVRCEwiKIAJ+iTyla2vTeAb1T963dd5oCfwPXgWvA\nKqDsLZ+7o5tFBADRwDFglFwSQRDymyDaACeADab3U9HNH7xM76uhT0b/HeBjer8JuITeKRzgF+AI\n0AgoB7xoEtkBclkEQchPgohJyNKBiaa/L9zy2Rz0Po63NoYVQx9H3c/0/jQw67ZtVjOtJwjCfbCU\nEOQ59qIP/xsLrAGW3vJZVSAOGHLbd64DlU3//wp8bCo6bwB+B05KWAXhwUi3m7zJ4tv+ZlIE8ADa\n3fbaAoSa1vkE6GrKGr8Fwk3FaFcJqyAI+a3IDFDd9P0ety3fjN6I8rBYAH3Qu+xMl8siCJIhFiQO\nA60Ap1uWWQFvA8XRvRk/ArxNn2UAK4B/0BthBEG4D1KHmL/4Br21eDN6S3MqMBS9/vAH9NbkbkBP\nU3E5xvRZd0zTHQiCIIKY34hG70sYeNvyMKA+8I5JCFPQ548eaBI/0Dtyj0DvyO2MPpOfHze78giC\nIDxVevBkdYiCIOQCUocoCIIggigIgiCCKAiCIIIoCIIggigIgiCCKAiC8PBIP8RHx5ObfoX3wtf0\n1wuo94B1o9HtuwRBEPId5dBHiKhser0oIRWEvIEmIXgs5gFDSpUqRePGjR/5y5cuXeLAgQOgextW\nQx9zLAiCkC8pDaQ4Ozsbo6Oj1aPSsWPHzOxwoIRSEISCwGxAffTRR48khgcOHFCapingAlKHKwhC\nAaGUpmkpTk5OxqioqIcWxC5dumRmh69ICAVBKEh8B6gPPvjgocTw0KFDmdlhIGAt4RMEoSBRXNO0\nJHt7e2NERMQDBbF79+6Z2eFQCZ0gCAWRaYAaO3bsfcXwyJEjmdnhZckOBUEoqBTTNC3R3t7eGB4e\nfk9B7N27d2Z2+JqETBCEgsxUQI0ePfquYnjy5EllMBgU+sx4thIuQRAKMkU0TUuwsbExhoSE3CGI\nffv2zcwOR0ioBEEoDEwC1MiRI7OI4alTp5TBYFCapoUDdhImQRAKAx6apsXb2NgYg4ODzYL44osv\nZmaHb0uIBEEoTHwOqDfeeEMppdT58+eVpaWl0jQtArCX8AiCUJhw1TQt1srKynjp0iU1cODAzOzw\nXQmNIAiFkQmA6ty5c2Z2eA1wkLAIglAYcdE0LYabfofjJCSCIBRmPgKUpmnRgJOEQxCEwowzEAX8\nT0IhCPkHmWQq5wQx0CSKgiAIhRIN8Nc0rnOzDvFPoIyERhCEwoQv8A+gLC0NasSIZqpq1aIKvS4x\nHngdmcNGEIQCjsGUFSYAqkaNYmrfvhFKqa9UauqXauLEzsrKysJoyhb/AypLyARBKIhUA/aYskLj\n2LGtVUrKl0qpr7K8jh17RzVoUMqULZIEjAUsJHyCkLeQh/LxsATe1TSWAmUaNy7Nxo2DtX796mBh\ncWc7VdGijrzySgMcHKzZseOSRUaGsT3wHLAPCJdwCkLeQOq0Hp1awEKgrq2tlRo/vr02ZkzLuwrh\n3bhwIYqhQ1ewdWsAmka6UkxF77eYKqEVBBHE/IItME7T+D+lsGzRoizz5/ehYkXPR96QUop58/bx\nzjvr1Y0bqRpwAngV2C9hFgQRxLxOU2ABUNnZ2VZ98kkHbcSIZhgMTxa+S5ei8fdfyZYt5wHSgZnA\nB8ANCbkgiCDmNexNxdl3AUPnzpWZPbsXpUq5ZtsOlFL8+OMhRo1ap2JikjQgAH1Wvn8l/IIggphX\n6AjMAcq4utqpSZM6a/7+jXJsZ2FhcbzxxhpWrz4BehedecAYIF4uhSCIIOYWrujTAQwFND+/mnz/\nfU88PZ+Og9fy5cd47bVVKioqUUMf/ucPbJbLIggiiE+bbprGbKXwLlrUSc2c2VPr1av6Uz+IyMgE\nxozZwI8/HjLrJDAciJZLJAgiiDlNUWAyMADAz68ms2f3wt09d13/N2w4zbBhK1VoaJymaUQoxevA\nKrlcgiCCmFP4aRqzlMLDx8eNuXP70L59hTxzcLGxSYwd+wfz5u1FKXO2+AZwVS6dIIggZhfe6N1c\numsaDB3aiKlTu+HoaJ0nD3bTpnP4+6/g8uVYNI1YpRgLzJVbWBCyj8I4dC/TomsdULN8eQ9WrXqZ\nN99shrV13g1H+fIeDBvWmIwMI7t2BdkqRTegAbAdiJNbWRAkQ3xUyqF3Z2lraWlg9OiWTJjQARsb\ny3x1Ejt3BjJ48HLOnr2KphGnFO+azkvJLS0IkiE+CEtghKaxEqhYs2Zx1q17hYED62Fpmf9Mw0uX\ndmXw4IakpxvZvTvIxpQttkG3F5OWaEGQDPGeVEcfdtfQxsZSjRvXRvvgg7Z5unj8KBw5Esqrry7n\n8OEraBpJSjEBvcXcKLe3IEiGmIkVNy26SjdpUoY//his+fnVfGhnmvxAsWJOvPpqAxwcbNi27aKl\n0ajaA+2BXcA1ucUFQTLE2ugWXXXs7KzUxx8/mkVXfuX48XAGD17O/v3BaBopSvExMAXIkFtdEAqf\nINoBH6OPAbZo2bIc8+f3oUKFIoXmgqanG/n++128//5GlZSUpgFHgMHAIbndBaHwCGJzYD5QydnZ\nVk2e3EUbOrQhmlY4u1oGBEQxZMgdRrQfAyly2wtCwRVEZ+BT4E3A0KVLFWbP7kXJki6F/uLew4h2\nMPrUBYIgFDBB7ATMBkp7ejqqKVO6aAMH1pOrehuBgTEMHbpCjGgFoYAKoiu6RZc/6GYMM2f2pEgR\nB7mi98kW87AR7U/o/pNVuXOMtr0psz0FdJUrKYggZqWbpjFHKYoXK6ZbdPXsWV2u5EMSHh7P66+v\nzmtGtB7ASWAj8Mptn00DBqH3Jw2RKyiIIOoUA74Demsa9O9fl2nTnst1i678yvLlx3j99dXq2rUb\nmUa0w4C/cvGQ+gDLgA7AFtOyhuj9KYehd64HqAz0Qq87vgL8TNbROU6mbZUF0oAdwDZkWKNQgATR\nz2Tc6l62rDvz5vXhmWfKy9V7Qu5hRPsaEJVLh7QCvQ9pDfS6zgPo81Y/axK0/sAidE/Is6Zidmmg\nBXABKGL6zlVgK+ACvIDuCjQml87JFaiL7q5UFH0YqZBzXAdCgYvoVS0FShB90Oc16WAwaAwZ0jBP\nW3TlV37//TTDhq1SV65cz20j2qKmovMCIBZ43ySOQSZxCzEVoT80rW9hEsALgJ9JMH8AHIFk0zqt\ngN7AKJ7ucMZuwFum/VvJXZYrBAJL0QcnPNSPfF4VRA0YqmlMVQrHatWKsmCBH40alZZLnEPkISPa\nzCwwHXgHmGVa3hb421RkPnvL+h+YhKcYeq+DP9D7W84BInIhlKWBJSYhxMnLiYptKuNW2h1re/kh\nz2mMRsWNq/EEHw4maP8llFGBxnVuOkLlO0H0NR14m/xs0ZVf2bTpHMOGrSQoKCY3jWj3AQ7oDSmZ\ndX+voA/HvBsKvTU62SSO75mKqPtNwj4TSHwKx90YjbUovLyrl6DTx12p1LYKmkGM6XODuIg4/vl6\nM3sW7VQZaRma6T4Ycb+SQl66UpbAG5rGl0phV6tWcRYu7EvduiXkyj5lEhPT+OSTzUyevA2jUWHK\nuobx9Fp5N5qKvS1uWdbHJG5NgMi7fCeIm2O2DUAz4DlgiKlI3ZicHdNdFo39KDwaD2pKj6/6YGFl\nITdTHuDKsRAW9ZunrofGasCXplJFnhbEGuj1Rg0yLbr+7//aYiU3VK6yc2cgQ4Ys58yZp25EezdB\nrAscRG+FvnVaVkf0DuYKva7OhawuP63QG1iqAGdy8Mf8EFCjzah2dP64m9w8eYyoS9eY8cxUlRiT\nCNAdWH+39XLb/sUKGKtpHAQaNGvmw5Ejo7Tx49sXSDE8cSKckJDrAFy/nszBgyGkpeVdI5pmzXw4\ndGgUY8e2xmDQnNHr5bYCuTEL12HgKPA5euML6PWG/5qOC3QfyO3o9XiZ93cj9PHbV3Lw2AYDNSq0\nqkinD6XveF7Eo2wR+s0doJmSwMnco7U/NzPEJuhmDFUzLbrefbcVhjxU3xIcHMtnn/2dZZmdnRW+\nvh688ELtR568vmLFr3juuapMmdKV9etP8dxzPxAS8n+UKJH3x13fw4g2p6zF7pYhgj4FxM/o/RPD\n0bvZbEbvuH0NvYvLj+jddK6athFvqjfKqVZzDbikGbQyo7a9i3d1qeLJy8zvM5uzf58GvTvWb3kh\nQ7QDJqJ3mK3asWNFTp8eo5mykDwVvGvXbjB37l6CgmKyLPvss7+pUGESJ09GFJobqXZtb/bufZOJ\nEztjaWlha7qG29FbfbMbP6DzXZZfNP2QlkBvUS6OPpwvs4gci97dxctUtK4OlCFnuxDVBcqUbeIr\nYpgPaDbU/Bvb8151H0+TFqassKKLi6366qsu5AeLrtdea0L37tXM769evUG5cl8yd+5epk9/DoD4\n+BQMBg0Hh5tdK5KT00lOTsPV1e6+279xI5Vz567i7GyLr69Hno2DlZUFY8e2pnPnyprJiLappnFE\nKSaairJp2bSrhAd8Hm563YsY0+tp0BqgSoeqojb5gAqtKmJla0Vaclqbu33+tDJEF1M9zzagYteu\nVTh5crTm798oX/oVeno64OHhwI0bqeZl7dvPY8SINVnWmzVrN97en913W+vXn6Zkyc/p3Hkh5ctP\nonv3H0hNzdsG1zVqFGPXrjeYNu057OysrdH7/e03ZUuFjVIAnuW9RG3yAZa2VriWcgPwBGxzQxA7\nA8cBfy8vR5Yt68/69a/ki3qzu5GcnM633+4kLCyOQYPqP/H2liw5yLlz7xEW9iEbNw5m3bpT/Pbb\n0bx/Y1kaGDmyOceOva21bu0LUAvYaypK2xSiZ8wTwKGIo6hNPsGxiBPodb9eT7PI7GZ6OG616NLy\no0VX//6/mlu9Y2KScHa2Ze7cPjRv7vPE23777Rbmxplnn61E7drerF59ggED8key5evrwT//+DNv\n3j5Gj95gkZCQMhboQt41ovVGH+uaXVgAGAwGUZp8guHm1MMWT0sQ/TSNmUpRpHhxZzVrVk/t1jq4\n/MaECR1o1aocAAkJqRw+fIX33vud48fDmDLlybpZVK1aNMv7cuXcCQ6+nq/io2ka/v6N6NChoubv\nv4LNm89XB3aj1xe/Q94yoj0NrAU+Qe+wLQg5VmQuBqxEt3Eq4u/fiLNn383XYpiZBdWrV5J69UrS\nqlU5Ro1qwYwZ3Zk6dfsTtzTb2WUd929lZUFqanq+jJOPjxt//TWUZcv64+Zmp5lKB8eANnnoMK2B\nAeiGs/PQu/IIQrYKogYM1DROAb3KlXNnyxZ/5szpjZNTwaxOKl7cCdANVwEsLDSSk7MKWeZn9yMs\nLC7L+8jIBLy98/d8MH5+NTl1aozWq1d1TILzN3qjmlNeOD4bGxvc3d2t0If1nUU3k8jRzuYxl6OJ\nCozK8oqLiMvR81z+1q/smr8jV2OdnpLO3J4zOffv2SfaTtipUOb2nElMsG59+dfEjfwxYX22H292\nFJnLog/+b2dhYeD115vyxRfPZul+UtCIi0vm6693YGdnRZ063iaBdObs2ZvGMAkJqSxffgyl7j/K\n7ZdfDtOsmY9ZDHfvDmL8+A75PkbFijmxcuXATCNarl274a9pdFOK4cC63Dw2Nzc3zp8/z4IFC/jy\nyy8tIiIiBgEDTaWbj8iBIX5Tm00kJeHOCQ+t7Kyp90IDOn/cDTsXu2zdZ9D+QKzscvc5VEpxfutZ\n6vZ9sgbI5OtJnN96llRTz46wk6GkJaXmKUHMtOj6WikcqlcvxoIFfjRsWKrACeDo0Rv49NO/TUKX\nQmBgDB4e9vz8cz+zY/dLL9Whd+8fad16NhUqFGHv3st07VqFmTN333WbmV1rYmKS6Np1EeXLe7Bh\nw2k8PR0ZMqRhgYmdn19N2rWroI0b9wdz5+4tjl5/l9tGtDg6OjJy5EiGDBmizZ8/n4kTJ2rh4eF+\n6N6Jf5iE8XB27rPpkBY8+383+5unJKQQsPMCa95dwY2oBAYuflXKrLnM4wpiefQK81YWFgY1enRL\nPvmkI9bWBWv8calSrsyZ0zvLMgcHa3x83Khfv2QWS7KePauzfftrbNsWgKWlBWPHtkHToHr1Yiil\n0DSNTz/tSJkyboA+8mPOnN68+moD1q8/xeHDobz1VjNefLEOHh4Fa1oENzc75szpzXPPVc00ovXT\nNFoqxRumrCzXcHBwyCKMkyZN0sLCwrqit5T/DoxHN5V4YqxsLbFzvXlt7Vztqfd8A6IuXeOfrzeT\nnpyGpa1epxwbEsPO+TuIOBOOraMtldpXoa5ffbOV2O6F/+Hg4Yh7aXd2LdxJclwSpeqUpumQFtg4\n3r2aKjEmkb2Ld3HleAgqQ1G8ujfN/Vti63wzM026nsTOedsJOXQZWxc7anSrRbXONW7+kCemsnvh\nToL2XUIZjZSu73PffZqzJ03j4NL9nNx4HIDqXWqas8b4yHh2zNpKk1ea4Vba3fydHbO24l7GI8v+\nbyf0xBV2zdtBXEQcxat50/qtZ54o07Z8jPVHaxqfKIV1nTolWLCgj1anTsEcslSkiAP+/o0eev3m\nzX3u6Ipz68iT55+vlWV55mc9e1anMEyU1aWL3iH/vfd+Z968vUXRpwxYjj6ndmReEMbhw4drixcv\n5pNPPtGuXLlyqzB+gt75PPuzEhtLjBnGTKs1Is9H8H3HaZSu50PtPnWJC7vO2nGruLw/kJ5T/AA4\nuvowKTdSURlG6vVrSHJcEn9P+YugfZcY9MvQO/ZhTDcyu+u3pky1OWga/83exokNx3hry2gMlgbS\nklKZ2Wk6BgsD9fo1JDH6Bj+9upiO73ei9chnSEtOY2bn6aQlptHi9dYA/Dd7G0fXHObNTW9jeR/P\n0t0L/sPe3YEqHaty5WgIvw77kYzUdBr0b0xi9A3+nbaFKh2qZhHE/T/tpWxT33sKYlxYHL8MXUKD\nFxvhUbYIW2f8TfDBIPzXvPFUBLEmukFnPRsbSzV+fAfGjGmJhYX0vxIeHhcXW+bM6U2vXjUyjWj9\nNI32uWREewc2Njb4+/szaNAgli5dyoQJE7SLFy92RR8zvQX4P7Kxf2X46TB2zf+PCq0rmR21N33x\nB64l3Hj1N39zRuhexoOfBy+m5Ztt8fDxwMLKgrCTV3j/8Ee4eLvqou7uwJr3VnLt4jWKlCuSVTzC\nr1OiVklavtGG4tX0em+vCl7M6votYSdDKVGrJPt+2svVgEg+PPmJuaO5rZMtJ/84TqsRbdn/0x4i\nzkQw7tD/zPus3L4qE+t+wuEVB2nw0r2TB6PRyCtLh5pHpsWFx7Fj1jYa9G/8RLF7d+8HeFbQ+1e7\nlnTjl6FLCDsVSvGq3jkmiLboQ7PGAJZt2vgyb14fLS+PuRXyPh07VuT48Xd4//2NzJq121UpNQd4\nCb0zf05miw/1C25tbc3AgQN54YUXWLhwIRMnTiQoKKgd0M5Ux/gpsOdRdrx3yR5ObDiWpfiZcDWB\n8q0q8vzMl8zLgw9eptIzlYm+fHMyQc8KXiiluHI0GA8f/dkrUbOkWZgAyreqiFKKiDNhdwiia0k3\nnp/5EikJKYSdCiUhMp74yPgsYhly+DLe1UtkGXXTeuQztB75jH5chy7jVcGL9NQMogJvVv8WKetJ\nyJHg+wpi1U7VswzT9W1ent/Hr8OY/vjT3HhW8DKLYeY2QW9wySlB9DUVFyoBfPNNN0aObJ4vxx8L\neQ8nJxu++64HffvWpFu3H4iLS24JtMxLx2htbc3w4cMZPHgw48eP54svvgB9OGpndCuyhy4ilW1S\njvov3Gww+338Oqp0rMYrv94s4iqluB4Wy8Gl+zm65kiW79u52pNw7abvhZNn1l5MDm4O5jq528lI\ny2DFqN84svIgriVccSnhhtHkxZnZE+J6aCz2bveuv74eGkvE2XCmt5lyx2dJsfefocHJ0znLe3s3\ne5RRcSM64fHvHy+nO+IDkBD5+FOMP0gQLwKTNI1vlMLl++93Ubu2N6axq4LwxFy6FM0nn2whLi4Z\ndNfrc+gz7+WUw0Uv7jJk634EBQXx+eef88MPPwCgaVq0Umoy+jzh8x92O14VvKjZo/bN4rmTDfP7\nzOb4+qPU6FYrc9s4uDvQ6OWmdPyg8323l3Ija7eT1ET9vb3rnaK2c94Ojq46xFv/jDZnT1cvRPJV\ng89vCoqbPdevxN5zf/YeDpSu78Prf7z1yEFPTUy541g1TcPO2Y7E6LuLaVrK/c2TUpOyfp5mOn87\n18dvlHyQICpgkVJsBL67cCGqd9u2cxg6tBGTJ3fB2dlWnmjhsVBKMW/ePt55Z726cSNVQ59D92mM\nf056WEEMCQlh8uTJzJkzR6WkpGiapiUA3yulvkSf//eJqPRMFWr1qsPqMSvwbVYee3c9w/Ms78Xl\ng0F3ZHiR5yLM9X8AEWfCyEjLMM/dEn4mTK9v9LmzOivsxBWKVi6WpSh57p8zpmthKoL6enHu7zOk\nJqaa6zNPbzrJwd/202/2ALzKF+XcP2ezfJ5ZRPWqWPS+c8iEnsg6fDziTDjOxZyxtLUyt1AnXL2Z\nLSZG3zB3wr4XV89HkpachpWpZT7irO4I5+Hz+NV5D5vuh6NP8tMXuDZ37l4qVZqs1q49KU+28Mhc\nuBBFmzZzGDZsJYmJqRnAJKA+ecQMIjIyknHjxlGhQgU1Y8YMUlNTE4FJSqlSwLjsEMNMun/Zi/SU\nNNa+f9PDtpl/S87/e5Zt3/7DjWsJxIbEsGr0MuZ0/y5L0TQj3cjvH68j4Wo8UYFRbP5qE8WrelOy\n9p19gYv4ehJxNoKgA4EkXU/iwK/7OL/tHJqmEWkSkvovNiIjLYNV7yzj2sVrBB8MYv3/1pCWlIaF\ntQUNXmpERmo6K95aSnRQFEmxieyct4NprSYTtD/w7j98ppbz8/+e4diaIyTHJ3N+2zkOrzxEvX56\n9YFzMRccPBw4+Nt+rgVc5eqFSFaM+g1HD0dUxt3rGFWGEYOFxroPVhMfGUdsSAx/fv4HHmWLULbJ\n45dgH7XbzXKl2AJMDA+P9+/RY3Gmiw1Py8UmNTWD48fDKF++CC4u+StDPXkyAhcXW0qWdCmUQpie\nbmTq1O189NEmlZqaoQFHlOJVsrkD9ONy9epVpk6dyvTp01VycrKmaVoi8J1SahJPaDjrXtoDOzeH\nu9SDOdPlk+78+81mgg4EUqa+DzW716bvd/34++vNbPhoLZY2VpRtXJZha9/MUhws37ICtk62fNXw\nC5JiEylRqyT95g0wf+5awhUHU9bZfFgrgg9dZnbXb9E0jepda/LCrJf4/eN1/Dv9b4xGxTPvtGfw\nsmGs/98aJtX7FFsnW6p2qk73L3sB4FbaHf+1b7Dh/9Ywqd5noEHRSsV4acHLlGt6dxEypmfg4eNB\npw+7cfC3/fw8dDGaplHzudo8M1ofkWWwNOD37YusHbeSSfU/w7WkG90+64GVnRW2pj6FljZW5tZ1\nvXjvQJ0+9XDxdmVK4y9JjEmkeFVv+i94+YmmfX2S1pHOwGyglJeXo/r++55anz41cvymvXw5ljJl\nvuD331+lc+fK+UoQKlWaTNeuVZg69elPRHT+/DVmzPiP06cjsbXVhxyOHNn8qf2QHTsWxuDByzlw\nIARNI1kpxpNzc7Lct8hcrFgx27CwMPOCa9euMWXKFGbMmKGSkpI0TdMSlVLzgS948GT3S4HnR2x+\nh9L1y2T7wRrTjbfaVZmZ12smNk625tEtxgwjhofoApdd6ymlUEb1UNu6/Xso7ilaD3t8T/K92c99\nR8CO86CPs7/0OEXmu/EH+vShcyMjE/Dz+5Fu3RYRGhqHkLt8+OEmJk/eZn6/d+9latb8mv/+C6RJ\nkzJUqeLFokUHqFZtqnkWwJwiOTmd8eM3U7/+DHXgQAjAf0pR21RMzlVr8KioKMaPH0+5cuXUpEmT\nSE5OTgZmKKV8gZEPIYY5zt3E8K7rWTzd9TRNeyzh0jTtvhmc4TH7NRuyqT/0k27lOvoE5q2B8xs2\nnKZq1Slq7ty9T+VmSUvL4NixME6ejMhiopCebiQmJomM2+ofrl9PJsnUMpWamkFMTJI56wwM1EtE\nMTFJpKZmoJTizJlITp6MuKel//nz1zh4MIRr127cowh2g4MHQ4iMfLSuBZcvx3LwYAgBAXcO9Y2J\nSSIlJaurzo0bqcTHp5jP8d9/A4iJSSQmJgmlFO+++zu1a3uzf/9bfPppRyZP7sK+fSNISEjh559z\nrrS6e3cQdetOY8KEzaSnZyQAo9DnST6bmyKTmprKhx9+iI+Pj5owYQIJCQkpwDSlVFmTEIbLz2rh\nJLuGmWwH/Vf/+vVk47BhK+nceSGXL8fm2IEfPx5O2bITefbZBdSs+TV16kwzC89//13C3f1jzp+/\nluU7lStPZtKkrQBs2HAad/ePWbLkIGXLfsnYsX8AUKTIeObM2UPDht/Stu1catf+hnLlJnL6dGSW\nfVerNpUGDWbQr98vlCjxGa+9tor0WzqZTpmyDW/vT+nRYzE1anzNuHF/8KDumxERCbRuPZvy5Sfx\n4ou/Ur36VOrWnZ5FGL28JjBvXta2h+HDV9G58wIAWrSYya5dQUyb9h++vhNJSEild+8aTJ7cFctb\nsg1vb2dKlXIlJCT7r1FiYhrjxv1BixYzM+O2USmqA9MBY27f9NHR0Xz22WfcuHEjDfjWlBG+nRcy\nwoel52Q/ukzoLgqWRwURIBG9Ba4lcHrjxjNUrz5VTZ/+n3mMZnYya9Zu/vprCKGh/+PkydEEBcVm\nKSY+iEwjit9+O8rx4+8we3Yv8/JJk7by3Xc9CA39H5GRHwMwdep2c2b53HOL8PX1ICzsQ86de489\ne95kyZKDzJjxHwBXrlzn/fc38v77bQkO/j/Cwz8kOTmdS5fu341g8ODlhIRc59KlcZw9+y6hoR8C\nMGDA0keoq3sHT08Hxo1rQ3T0BJycbBg5svkdY6xPnAjnwoUos/VYdrF9+0Vq1/6GSZO2YjSqzBJE\nZ+ByXrnpNU1LA2aZhPAtsndKgadCEV/PJ+peIuS8IGayC332tQkJCSkZo0ato3Xr2Zw7dzVbd9K/\nf12z/X7lyl50716VVauOP/yJm+oxXn21AVWrFsXNzc68vEuXyjRqVBrQnVoaNChpzja3bbtIYGAM\nEyd2Mrtd16lTghdeqM2vvx4BYPXqk2RkKN5+u4W53uTjj9uTkXHvH4a4uGT++OMMb77Z1DwBl5ub\nHSNGNGP37qBsrZvdvv0iHTrM55VX6mcxnHiiupPryQwbtpLWrWdnxmqDUlQlD4xPvo35SqnywOtA\niEiAcCs5NadKMjBeKVYDC3fsuFS3Vq1pavz49lp2GUJUrZp1wqyyZd1ZuvToAw1Z79xO0TuWlS+f\ndRyou7u9WZAyi69ff70DCwstS8aVmQGGhMTi6mprFtlMccucTOpuBAXFopSicuWs51Whgn4sgYEx\neHs7P3Hcliw5yJAhK5g4sRPvvJM9o+R+//10pq2XpmlEAm+gO9nkRUbIYy88bUHM5CjQCBidkpL2\nybhxf1ivWXOCBQv87ipEj8Ltc5FYW1uSnm68b/H8bmJ5N2fvW4XudjIbNHx9PcxZJkC5ch7mfSQl\npd/VG/J+PwSZjT23f8/KSv9OcnLaI53XXes0EtN48801fPBB22wRw8jIBMaM2cCPPx4CvQvXcqVy\n1/g1F0gASLmRImqST0iJTzYXzJ62IAKkA5OUYgOwYM+ey41q1fpGjR7dUnsSU9mwsPg7Hs6iRR2x\nsDCYhefWOU7S0jKIikp84pPJNHjt378OpUq53nWdYsWciIpKJC0twzx9aVJS2n1bmzO3e3s3mMz3\nPj7uZlG9vZX5YeZuAUhNTWfKlK4891zVJ47D8uXHeO21VSoqKlEDAtHrCv8qhM9XKOiOMUL+IC7s\nOkAKcEel/tM0MzwJNAWGZWQYkyZN2kqDBjMw9U17ZH777ai5W01qagYbN54xm04UL64XLW+tt1yy\n5OB96/AelqZNy2Bra8msWVmnBnj33d+ZN2+veZ30dCPr1p0yf7548UHS0jLumc0VLepItWpF+emn\nQ+YsVynFkiUH8fFxw8fHzXRuTlnmbjl37io7dwZy62YtLAxcv558xz4MBo169Upgb2/12OcfFhZH\nz56L6dv3p8wfmLnoXpl/FdLn6xTApd0BojT5gGsBVzMn9zqJ7tXw1DPEWzECc03D/+YdOxbWtkmT\n7xg9uiUTJnTIYsl/7yxH7xNYooQzLVrMolGj0uzcGUhwcCy//dbfVJx1p3Hj0rz++mo2bDjNjRup\nKAVVqng98RSfXl6OTJ/enddfX82RI2FUruzJ/v3BnDoVyaZNQwBo1aocLVqU5eWXf2PNmpMkJKQQ\nHh5PtWpFSUu7d1/k2bN706nTfFq2nEWDBqU4cCCYw4dDWbPmZXPx/KWX6jJx4r9cvZqAq6sdR46E\n0rNn9Sxdc6pVK8qSJQcJC4tjwoQO5nrIffuCad9+Hps3D6Vdu0ebZE4pxY8/HmLUqHUqJiZJAwKA\nocC/hfwZ2wiknvzjhHWPiTenABDyJkfXmPvd3nXKvtyaBCUG+BEIVUq1+e+/QOulS49Qq5a3ORO6\nFwaDRrlyHrz9dkvq1i1BWFgcNWoU47vvelClit4goWka/frVxsvLEYPBQIsWZRk/vj0lSrjQoEEp\nSpZ0wdbWksqVvWjYsHSWYnvx4s60aFGOokVvmmS6utpRv34pc4NHvXol6du3prnOslUrX77/vkeW\nxph+/epQurQrGRlGGjUqzVdfdaFcOQ/q1y9pLh7fTunSrgwaVB8rKwsSE1Np1qws33/fk1q1bjqU\ntGnjS61a3iilKF++CF991ZmKFT2pWdPbfP4dOlTExcWW8uU9aNiwtLm+1cbGkkqVvGjatMwjORVd\nuhSNn99PfP31DpKT0zPQba/6AOflESMFqJmamFrNztUen4ZlJSJ5lKTYRH4avFilp6RlmKp47igy\n5wWnV29gFvCcwaAxZEhDpk7thqOjtVzBXMZoVMyfn8Wi6zi6Rdd+iU4WKgInbRxsLN7c/LZWrEpx\niUgeQynFL0OWcGTVIUx683peyhBvJR59gPwp4JmDB6/YLV16hOrVi1GunLtcyVzi5MkIunf/gdmz\n95CenpEBTAb6AcESnTuIAtIz0jLand18WlXpWE27n/O08JTF0Kj4Y8J69vywC1NVTz90X8w8KYiZ\nnAIWA2VjY5Oq/vjjQQIComjd2veOLjZCzpGebmTy5G288MLP6vLlWA193pBOwK/kshlDHmcnUC7p\nelKtQ8sOKPcyHlrRysVkuo1cJvZKLEuH/8T+n/eCRizQgfuMmsqrV6ubpjFHKYoXK+akZs3qpfXo\nUU2ubg5z9GgYr766jEOHruS2RVd+xYA++dT7gFaqbmnq92tIxbZVcCvphkUBm7c8r5IYfYOQI8Ec\n33CMg7/uU2nJaRpwBniOB9R75+WfLzf0Gdj8gaduRFuYSE5OZ+LEf/n8879VerpRA3YAQ9DnNxEe\nnVbAV0DDWxc+yVwfwsORlpRK+q39dDVuoJiCXuVz40Hfzw/5fCdgDiYj2u++66H5+dWUK59d5byd\ngQwZspwzZ66iacQpxUfAt+QBV5p8jgY0BroDTYDiQBEJS87/vgNhwAX0GUM3cJfW5PwsiAAuwCfA\nm4Cha9cqzJ7dy2yCIDxGsSIxjU8+2czkydsyO4L/AQxHGk2EQv4rlp9ogT7tY0UXF1v11VddNH//\nRnIVH5FNm84xbNhKgoJi0DRilWIsec+VRhBEEB8CO+BjYAxg8eyzlZgzpzelS7vK1XwAsbFJjB37\nB/Pm7c0c6rcc3ZnmqkRHEPJWt5uHJR3YAmwGml64EOW5YME+ZW9vrTVsWEq6OdyD9etP0bnzQrV1\n60VN04gAXjZVQyRKdAQh/2aIt2ILjNM0PlAKq+bNfViwwI+KFT3lypqIiEhgxIg1LF9+DPTB7D+h\nz20SLdERhPyfId6eLW4F1gINL1+O9Z4/f5+ysrLQmjQpncWvsDCyfPkxOndeoA4cCNHQp1vsC0zl\nHr30BUEyxIKDJTBa0/hEKawbNy6dLUa0+ZHQ0Dhef301a9eezMwK5wGjMZmZCoJQMDPEWzGiD59a\nDdQLCblecu7cvSoxMVVr2bJctkxbkNdRSjFv3j66dftBHT8epqH3xeqN7k6TKre7IBSeDPFWDMAQ\nTeNrpXCoWbM4Cxb4Ub9+yQJ7IS9ejGbo0BX888+FzKqEqeit8eJtLwiFMEPMkiwBB9FddKpHRCSU\nW7RoP4mJqbRoUTbL/MT5nfR0I99+u5M+fX5U585d1YBjQDd0v0kZgywIkiHecY5DNY0pSuFUvrwH\n8+f70apVuXx/YidOhDN48HL27QtG00hRionAF1I8FgTJEO/HQXRrsfLR0UmVFy8+QGhoHG3alH/s\nSa5yk7S0DKZM2c4LL/ysgoNjNfS5sLugT/0pWaEgSIb40PhpGrOUwqNsWXfmzu39yPOL5CaHD19h\n8OAVHD58BU0jSSkmIBZdgiCC+AQUxTQviKZB//51mTbtOdzd8649U1JSGhMmbGbKlG2ZswduR7fo\nknlNBEEEMVvIF0a0//2nW3SdPWu26HoXvW+hkltYEEQQsxNXYBJ50Ig2Li6ZDz/8i+++25lp0bUB\neA0IkcsmCCKIOYnZiNbT01FNmdJFGziwXq4dzMaNZxg+fBWXL8eiaVxVijHAErlMgiCC+LRwRp8T\nI9eMaGNikhg37g/mzt2buWg5+pSJ1+TyCIIIYm5whxHt0KENc9xabP36UwwbtkqFhcVpmka4UrwG\nrJHLIQgiiLnNUzOiDQ+P580317By5XG4adE1EoiRyyAITw+ZF/He3GpE2+TChSjPOXP2KEtLC61p\n0zLZli3qFl0L1aFDVzTgIrpF19fok+UIgiAZYp7DCnhH0/g004h2/nw/KlV6fCPawMAY/P1XsHnz\nedCdeuYjFl2CIBliPiDTWmwt0OBJjGgzLbp69FiszpyJ1ICT6FNVzkbGIAuCZIj5jMc2og0IiGLI\nkBVs3RqAppGulFh0CYJkiAUjW1wK1A4JuV7mQUa06elGJk/ehp/fTyogIEoDjiAWXYIgFDAMgL+m\nkQCoGjWKqf3731JKfWV+HT36tqpfv6QClKaRBIyVHyJBEAoyZdFbpJWlpUGNHdtaxcV9qiZO7Kys\nrCyM6F1p/gMqS6gEQSgMaMBwTSMOUDY2lqasUItHH38s9bWCIBQ6SqEb0ir0qT9LS0gEQSjM9DAJ\n4jQJhSDkHwwSAkEQBBHEvEhRdF/G1vf4vDW6TZkgCDmApYQgT1EO3ZPxBlADvQ7yVgYBXsBGCZUg\nSIZYWAgGpksYBEEEUdBNHjoDfR6wnjXwpSmTjDf9/dK0XBAEKTIXCI6izwo4A91+7Po91puJ3qI9\nGNgPNAAWAi7oLtuCIEiGWCD4EN2TceI9PncFXkafk3ktEGr6+x3wCmArIRQEEcSCQjwwHL3Vudld\nPvc1Zfh7blt+yCSGpSSEgiCCWJD4A31OlTncWS9Y5BbhvJW42z4XBEEEscDwlinbe5esvolXTH89\nbls/08Zb5m4WBBHEAscV4P+A/wElbll+wZQNdrxt/Q5A5C2CKQjCQyKtzPmDmUB/oAs3O2UnA5+g\nN7rEo9cdtkDvvP0aupGtIAgiiPmWCGAu+kiVWzECQ4E3gRO3LJ8KXAb6Ae1MxeRuyEgWQRDyED0Q\ntxtByHdIHaIgCIIIoiAIggiiIAiCCKIgCIIIoiAIggiiIAiCCKIgCIIIoiAIwuMiI1UenbJA/Qes\n08D0twLg94B1A9HNXQVBEPIdxdCH1qlsenWWkApC3kCTEDwWk4Ex5cuXp3fv3o/85UOHDrF582aA\nA7dkk4IgCPmSIpqmxdvY2BhDQkLUo9KsWbPM7PA5CaUgCAWBLwH11ltvPZIYbtq0KVMMD0uGLghC\nQcFD07R4a2trY3Bw8EMLYosWLTIFsZeEUBCEgsRngHr99dcfSgy3bNmSKYYnkC5PgiAUMFw1TYu1\nsrJSFy9efKAgtmrVKlMQ/SR0giAURMYDyt/f/75i+N9//2WK4SnJDgVBKKi4aJoWbWlpaQwICLin\nID7zzDOZgthPQiYIQkHmQ0ANHjz4rmK4a9euTDE8B1hIuARBKMg4app21cLCQp09e/YOQezYsWOm\nIA6QUAmCUBh4H1Avv/xyFjHcs2dPphheQMaOC4JQSHDQNC3SwsJCnT592iyInTt3zhTEVyREgiAU\nJt4D1EsvvaSUUurgwYNK0zSF7mhjLeERBKFQZYlAuMFgUMeOHVPPPfdcZnY4VEIjCEJh5G1ANWzY\nMDM7DJLsUBCEwoqtpmlXuOl3+JqERBCEwswIkxgGAzYSDkEQCjM2JjF8U0IhCPmHvO7HZwn4AkUB\nL/KXf2Aj4BCQlo+OORYIRa/3TJDHQxDyBs2Bn4Bosm/uEnk9/CsZ2Ai8hBhRCJIh5hrewCxM1vpW\ntlb4NCqLc3EXnLyc0QxiMJ2TJMbcIC48jssHgrgRZU4QjwLDgT0SIUEE8elRH421KLzdfTzo+H5n\nanSriZWd9Fh52hgzjFzaFcBfEzdycVcAaKSiGAoskegIIog5TwU09qJwazyoKT0m9cHCWkxh8gJ7\nftjFmvdWqIy0DIA+wCqJiiCCmHPYoE+4VKXNqHZ0/ribXJU8xum/TrKo3zxQ3FBK1UW3MROEAkde\nSMNGAi9VbleVvt/2Q9OknjCv4enrhcHSwIXt56yBUsBvEhWhIJLbLYhWaHxgsDDw3Bc9pdEkD9Pq\nzba4l/EA6AHUkogIIog58Jyh8KjSsRqeFbzkauRhLG0saTa0Rebb3hIRQQQx++kAUK1zDbkS+YCq\nnWpkuW6CIIKYvZQBKFa5mFyJfECRckWwsrUyXzdBEEHMXrwAHD2d5ErkExy9nAA8kREsgghitmMF\nYLCSPof5BQv9WlkgswcKIoiCIAgiiIIgCCKIeY305DSSYhPveBnTjbl6XGc2n+KXoY821Dcx+gY/\nvrKIK0dD5E4UhDxAvpsneOe8HWz4aO2dym5pwLtGSTp/1JUKrSvli3NJS07j2Joj1H+hISVqlZS7\nURBEEB+P0bvGZXHCiY+M4+8pf7Hwhbm89fdoilfzfqrHU7l9VSq3ryp3lCCIID593Eq7Y+Nwc7oS\nDx8PBi5+hQ99xnF8/VGzICqlOPn7cU5tOklKQjJFynnSdHBzXLxdAbgWcJV9P+2h9Yi2HFx2gOAD\nQTh6OVGrZx3KNPC5WbyNSWT/T3sIOxkKGpSsXYpGLzfN7JfHpT0XObvlNM/+rwsA/3yzmbJNfIkO\niuLMX6fo9XVf7FzsHnheUZeuse+nPcQERWPtaE35lhWp1bOOeYz34RUHUUZF6Xpl2DFrK0nXk6jQ\nqiIN+jcmaH8g+37cjTFDUbN7Lap0qAbAlaMhHF1zmGfGdGDn3O2EnQjFtaQbdfvWf+o/HIKQlylQ\njSoW1pYYLCxIS77p2r/+g9UsHf4TbiXdqNimMiGHL/NNy6+ICowC4HpoLP9O28JPr/5AxOkwStYp\nRciRYGZ1mcGVYyHmou33z07j0LIDlKxTCu/qJdj+/VYWvTAXpRQAIYcvs+27f8373fPDLnbO3c6W\nyZuwtLEE03r34+qFSKa1nkLYyVDKNi2Hc1EXVry1lD8/+928zpm/TrFr3g6Wv/UrHuU8sXawZtmI\nX9nw0Vp+/2gtxap6k5qYwqIX5pmP/2pAJP9O28KSgQuJC4+jZJ3SnN92lu86fENMcLQ8BYKQ3zPE\n2zGmG9k86U/SklKp2lHPjCLOhrNj9jb6LxxErZ51AGjwYiOmNp3I31P/ou+3/cx9ID3KFqH3N88D\n0GxoSz6r/jH/zdnO89+/SGxwDMWre9NhXCe8KhQFwL2MB4sHLCA6KBoPH487xdnKgoD/LvDevg+w\nc7V/qHOICrxGpWcq02/OgMz+fqSlpLHvxz10+rCr/gtmaSDkaDDjDn2Ia0k3AC5sP8/+n/bwwfHx\n2DjY0PTV5ny8+X3Obz1LiZolMVjov3tl6vvQ4f1OADTs34hPq3zE7oU7xXJNEPK7IM7qPMPsjpOR\nmmHOdHpM6k3ZJr4ABB8MQtM0fBqXIyk20fxd3+blCdx7Kcv2qneteUumaYFv8/KEnbwCgGcFL/ov\nGER6chqR5yNIvZFKSkIKAHFhsXcVRE3TKN+iwkOLIUDldlWp3K4qyfHJRJ6PICM1A2VUJFyNJyM1\nQzfN1TQ8yhYxiyGAawlXPH29zFUIFtYWOBV14kbUjXueo52rPaXqltarAARByN+C2OL11ljZ6PV3\nQQcC2TFrKyP/GZOltTb2SixKKT6r+tEd37+9Pu/24YMO7g4E7rkI6F19Vr6zjMMrD+Lk5YxTUWcM\npjq9+5WEnbwebUhibEgMv73xC5f2BOBe2gMHdwcSbxFy87E7Zz12g6UFts62WZdZWJiL8+ZzvO14\nHDwcpcgsCAVBEKt3rWnOiKp3q8nFXQGsGrOMN/4cZS4i2rs7YLAw8GX4VAyW968uTU1MveO9rUl4\ntn77Dyc2HOPt7e9RtJJuRBFy+DLT20697zY1i0erol01ejk3ohL46Mxn2LvpmeWu+TtY/e6KbIlZ\n6o3bzzHFfI6CIBSQRhWDhYE+3zxPyOFgdszcal7u6euJMcPIlaPBWdaPuRydpeEFuKPoGHEuAndT\nUfjKsRBK1iltFkOA89tMLvoP0VjysFw5GkyVDtXMYghwfutZ026efD+ZVQCZ24s8F3nX4r4giCDm\nc0rUKknzYS3Z9MUfXL0QCYBv8woUrVSMVe+uIOJsOBmpGVzceYFv23/D1ul/Z/n+3sW7CDkSTHpK\nOoeWHSDk0GXqPd8A0Lv0hB4PIfJ8BGlJqRz4ZS8XdwYAcDXgaradg7tPEc5vO8uNqBskRt9g46cb\nSLqeBMC1i0++nx2zthF5LoL05DR2zNpGTHA0dU3nKAhCPiwyW9paYedqf9e5Vzp80Jkzm0+z4cO1\nDPplCAZLA0NWDGf1uyv4psVXZKRl4FDEkUYDm/DM6Kwep21GtWPZm78QdjIUK1srWrzemprdawPQ\n+q1nCD4czJTGX2KwMFCze21eWvgyS4f/xNpxq0hNTNWP65Z6SRsnW3MfxXsWqQ0adq72GCz1FuXu\nE3vxi/8Sxpf/AFsnW5oPb8XAJYOZ1WUG37X/hsHLh2FtZ4WNk02W7dg4WGPtkHW6VhvnO/ffakRb\nFvWby7WL17BxtOHZD7tSrqmvPAWCkPlM5vL+/wOa/e/UJ7gUd8nRHRnTjaSlpGXpzA16h+qZnaYz\netc4ilUpTlpSKhZWlnetc0xPTsNgZWGuo8wpUhNTsbbPvvmoj609wo+DFjH+whc4eDiQmpiKla3V\nY81hM6n+Z1zTs2JrIE0eIUEyxPxYN2BpwMbS5oHr3Toc8G7Z6dMgO8UwN7YvCPlWJyQEgiAIIogA\nFKtSHP/Vr+NW2r3AnmO5pr74r379jr6KgiAU0iLzvbBzscs3dmGPi6OnU4E/R0GQDFEQBEEEURAE\noeAJYhJAWpL03sgvpOlDHFOBdImGIIKYvYQCxEdclyuRDzBmGIm/Gg8QBiiJiCCCmL2cB7h8IEiu\nRD4g5HBw5mRe5yQagghi9rMB4Pi6o3Il8gHHNxzNct0EQQQxezkCnAw6EMi5f87I1cjDJFyNZ/eC\n/xQaKcBKiYgggpgzfACw5r0VZmcXIW+hlGL1eytISUjRUHwLXJGoCAURizxwDGeBmokxiVWuHA2m\nRrda5vlEhLwhhn9++jt7ftgFcAEYACRLZISCiJZHjsMR3fmmVvHqJXhp/sAsZqxC7pAYfYNV7y7n\n6KrDoBGHojFwWiIjiCDmPG7Ar0BHg4WBei80oI5ffXyblX+g/b+QvYSeuMLxtUf5b842lRyfrAEB\nQHfgpERHEEF8ukX4N9D4CIUH6NN5Onk53TEJlJD9pCSkEHsllrSk1My7Iw3FTGACECMREkQQcwdn\noI8pK6kHFEWMKJ4Wkej9DNcBywDpJCqIIOYxDICLXK4c5wb6sDxBEARBEARBEARBEARBEARBEARB\nEARBEARBEARBEARBEARBEIRH5/8BcklnLIETtEwAAAAldEVYdGRhdGU6Y3JlYXRlADIwMjQtMDYt\nMTZUMjI6Mjg6MjYrMDA6MDDyqubSAAAAJXRFWHRkYXRlOm1vZGlmeQAyMDI0LTA2LTE2VDIyOjI4\nOjI2KzAwOjAwg/debgAAAABJRU5ErkJggg==\n" + } + }, + "id": "7d7cbc20-956e-4d51-baf0-cee578b3a038" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_3/ForwardFiniteDifference b/tutorials/module_3/ForwardFiniteDifference new file mode 100644 index 0000000..128bb56 --- /dev/null +++ b/tutorials/module_3/ForwardFiniteDifference @@ -0,0 +1,37 @@ +#!/usr/bin/env python3 +# -*- coding: utf-8 -*- +""" +Created on Thu May 8 13:27:05 2025 + +@author: christian +""" +import numpy as np +import matplotlib.pyplot as plt + +# step size +h = 0.1 +# define grid +x = np.arange(0, 2*np.pi, h) +# compute function +y = np.cos(x) + +# compute vector of forward differences +forward_diff = np.diff(y)/h +# compute corresponding grid +x_diff = x[:-1:] +# compute exact solution +exact_solution = -np.sin(x_diff) + +# Plot solution +plt.figure(figsize = (12, 8)) +plt.plot(x_diff, forward_diff, '--', \ + label = 'Finite difference approximation') +plt.plot(x_diff, exact_solution, \ + label = 'Exact solution') +plt.legend() +plt.show() + +# Compute max error between +# numerical derivative and exact solution +max_error = max(abs(exact_solution - forward_diff)) +print(max_error)
\ No newline at end of file diff --git a/tutorials/module_3/finiteDifference.py b/tutorials/module_3/finiteDifference.py new file mode 100644 index 0000000..10470f1 --- /dev/null +++ b/tutorials/module_3/finiteDifference.py @@ -0,0 +1,34 @@ +#!/usr/bin/env python3 +# -*- coding: utf-8 -*- +""" +Created on Wed May 7 10:25:47 2025 + +@author: christian +""" + +import numpy as np +import matplotlib.pyplot as plt + +# Initiate vectors +t = np.linspace(0, 30, 5) # simulate for 20 seconds +v = 42.78 * (1 - np.exp(-9.81 * t / 42.78)) + +# Forward difference method +dvdt_fd = (v[1:] - v[:-1]) / (t[1:] - t[:-1]) +dvdt_bd = (v[1:] - v[:-1]) / (t[1:] - t[:-1]) +dvdt_cd = (v[2:] - v[:-2]) / (t[2:] - t[:-2]) + +# Plotting +plt.figure(figsize=(8, 5)) +plt.plot(t, v, label='Velocity (m/s)', color='blue') +plt.plot(t[:-1], dvdt_fd, label=r'forward difference') +plt.plot(t[1:], dvdt_bd, label=r'backward difference') +plt.plot(t[1:-1], dvdt_cd, label=r'central difference') +plt.axhline(y=42.78, color='red', linestyle='--', label=f'Terminal velocity ≈ {42.78:.2f} m/s') +plt.title('Falling Object Approaching Terminal Velocity') +plt.xlabel('Time (s)') +plt.ylabel('Velocity (m/s)') +plt.grid(True) +plt.legend() +plt.tight_layout() +plt.show()
\ No newline at end of file diff --git a/tutorials/module_3/notebook_3/numerical_differentiation.ipynb b/tutorials/module_3/notebook_3/numerical_differentiation.ipynb new file mode 100644 index 0000000..0892554 --- /dev/null +++ b/tutorials/module_3/notebook_3/numerical_differentiation.ipynb @@ -0,0 +1,140 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "id": "d66e2b4b-047b-4670-897d-7877d27a1597", + "metadata": {}, + "source": [ + "# Numerical Differentiation\n", + "\n", + "Finding a derivative of tabular data can be done using a finite\n", + "difference. Here we essentially pick two points on a function or a set\n", + "of data points and calculate the slope from there. Let’s imagine a\n", + "domain $x$ as a vector such that $\\vec{x}$ =\n", + "$\\pmatrix{x_0, x_1, x_2, ...}$. Then we can use the following methods to\n", + "approximate derivatives\n", + "\n", + "## Forward Difference\n", + "\n", + "Uses the point at which we want to find the derivative and a point\n", + "forwards on the line. $$\n", + "f'(x_i) = \\frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i}\n", + "$$ *Hint: Consider what happens at the last point.*" + ] + }, + { + "cell_type": "code", + "execution_count": 2, + "id": "d2fe3ad1-8af0-499a-8954-41a88a49b834", + "metadata": {}, + "outputs": [ + { + "ename": "IndexError", + "evalue": "index 99 is out of bounds for axis 0 with size 99", + "output_type": "error", + "traceback": [ + "\u001b[0;31m---------------------------------------------------------------------------\u001b[0m", + "\u001b[0;31mIndexError\u001b[0m Traceback (most recent call last)", + "Cell \u001b[0;32mIn[2], line 10\u001b[0m\n\u001b[1;32m 6\u001b[0m y \u001b[38;5;241m=\u001b[39m \u001b[38;5;241m34\u001b[39m \u001b[38;5;241m*\u001b[39m np\u001b[38;5;241m.\u001b[39mexp(\u001b[38;5;241m3\u001b[39m \u001b[38;5;241m*\u001b[39m x)\n\u001b[1;32m 8\u001b[0m dydx \u001b[38;5;241m=\u001b[39m (y[\u001b[38;5;241m1\u001b[39m:] \u001b[38;5;241m-\u001b[39m y[:\u001b[38;5;241m-\u001b[39m\u001b[38;5;241m1\u001b[39m]) \u001b[38;5;241m/\u001b[39m (x[\u001b[38;5;241m1\u001b[39m:] \u001b[38;5;241m-\u001b[39m x[:\u001b[38;5;241m-\u001b[39m\u001b[38;5;241m1\u001b[39m])\n\u001b[0;32m---> 10\u001b[0m dydx[\u001b[38;5;28mlen\u001b[39m(y)]\u001b[38;5;241m=\u001b[39mdydx[\u001b[38;5;28mlen\u001b[39m(dydx)]\n\u001b[1;32m 12\u001b[0m \u001b[38;5;66;03m# Plot the function\u001b[39;00m\n\u001b[1;32m 13\u001b[0m plt\u001b[38;5;241m.\u001b[39mplot(x, y, label\u001b[38;5;241m=\u001b[39m\u001b[38;5;124mr\u001b[39m\u001b[38;5;124m'\u001b[39m\u001b[38;5;124m$y(x)$\u001b[39m\u001b[38;5;124m'\u001b[39m)\n", + "\u001b[0;31mIndexError\u001b[0m: index 99 is out of bounds for axis 0 with size 99" + ] + } + ], + "source": [ + "import numpy as np\n", + "import matplotlib.pyplot as plt\n", + "\n", + "# Initiate vectors\n", + "x = np.linspace(0, 2, 100) \n", + "y = 34 * np.exp(3 * x)\n", + "\n", + "dydx = (y[1:] - y[:-1]) / (x[1:] - x[:-1])\n", + "\n", + "dydx[len(y)]=dydx[len(dydx)]\n", + "\n", + "# Plot the function\n", + "plt.plot(x, y, label=r'$y(x)$')\n", + "plt.plot(x, dydx, label=r'$\\frac{dy}{dx}$')\n", + "plt.xlabel('x')\n", + "plt.ylabel('y')\n", + "plt.title('Plot of $34e^{3x}$')\n", + "plt.grid(True)\n", + "plt.legend()\n", + "plt.show()" + ] + }, + { + "cell_type": "markdown", + "id": "a54ad04f-05e5-4589-a633-d6dea2a5acfc", + "metadata": {}, + "source": [ + "## Backwards Difference\n", + "\n", + "Uses the point at which we want to find $$\n", + "f'(x_i) = \\frac{f(x_{i})-f(x_{i-1})}{x_i - x_{i-1}}\n", + "$$" + ] + }, + { + "cell_type": "code", + "execution_count": null, + "id": "415d0b3c-a70d-48ef-93ad-6e827127b222", + "metadata": {}, + "outputs": [], + "source": [ + "dydx = (y[1:] - y[:-1]) / (x[1:] - x[:-1])\n", + "\n", + "# Plot the function\n", + "plt.plot(x, y, label=r'$y(x)$')\n", + "plt.plot(x, dydx, label=b'$/frac{dy}{dx}$')\n", + "plt.xlabel('x')\n", + "plt.ylabel('y')\n", + "plt.title('Plot of $34e^{3x}$')\n", + "plt.grid(True)\n", + "plt.legend()\n", + "plt.show()" + ] + }, + { + "cell_type": "markdown", + "id": "21c87595-add2-4f7a-8d10-2da3b4284e02", + "metadata": {}, + "source": [ + "## Central Difference\n", + "\n", + "$$\n", + "f'(x_i) = \\frac{f(x_{i+1})-f(x_{i-1})}{x_{i+1}-x_{i-1}}\n", + "$$" + ] + }, + { + "cell_type": "code", + "execution_count": null, + "id": "6a67e63c-9516-415d-87d6-97d9d986ba33", + "metadata": {}, + "outputs": [], + "source": [] + } + ], + "metadata": { + "kernelspec": { + "display_name": "Python 3 (ipykernel)", + "language": "python", + "name": "python3" + }, + "language_info": { + "codemirror_mode": { + "name": "ipython", + "version": 3 + }, + "file_extension": ".py", + "mimetype": "text/x-python", + "name": "python", + "nbconvert_exporter": "python", + "pygments_lexer": "ipython3", + "version": "3.13.2" + } + }, + "nbformat": 4, + "nbformat_minor": 5 +} diff --git a/tutorials/module_3/notebook_3/numerical_integration.ipynb b/tutorials/module_3/notebook_3/numerical_integration.ipynb new file mode 100644 index 0000000..1638ad5 --- /dev/null +++ b/tutorials/module_3/notebook_3/numerical_integration.ipynb @@ -0,0 +1,27 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "## Midpoint Method\n", + "\n", + "## Trapezoidal Method\n", + "\n", + "## Romberg Integration\n", + "\n", + "## Gaussian Integration\n", + "\n", + "## Simpson’s Rule\n", + "\n", + "### Simpsons 1/3\n", + "\n", + "### Simpsons 3/8" + ], + "id": "81ed366c-8dc9-4d6c-9a5e-36a28f7811b5" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_3/notebook_3/numerical_methods.ipynb b/tutorials/module_3/notebook_3/numerical_methods.ipynb new file mode 100644 index 0000000..e5bf7df --- /dev/null +++ b/tutorials/module_3/notebook_3/numerical_methods.ipynb @@ -0,0 +1,52 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Numerical Methods\n", + "\n", + "Engineering\n", + "\n", + "## What is a numerical method?\n", + "\n", + "Numerical methods are techniques that transform mathematical problems\n", + "into forms that can be solved using arithmetic and logical operations.\n", + "Because digital computers excel at these computations, numerical methods\n", + "are often referred to as computer mathematics.\n", + "\n", + "## Numerical Differentiation\n", + "\n", + "Forwards difference Backwards difference Central Difference method [Read\n", + "More](https://pythonnumericalmethods.studentorg.berkeley.edu/notebooks/chapter20.00-Numerical-Differentiation.html)\n", + "\n", + "## Roots and Optimization\n", + "\n", + "Incremental Search Bisection Modified Secant Newton-Raphson\n", + "\n", + "## System of Equations\n", + "\n", + "Guassian Method LU Decomposition\n", + "\n", + "## Numerical Integration\n", + "\n", + "Midpoint Trapezoidal Romberg Gaussian Simpson’s Rule\n", + "\n", + "[Read\n", + "More](https://pythonnumericalmethods.studentorg.berkeley.edu/notebooks/chapter21.00-Numerical-Integration.html)\n", + "\n", + "## Numerical Solutions of Ordinary Differential Equations\n", + "\n", + "Euler’s Method - Forward - Backwards\n", + "\n", + "Runge-Kutte\n", + "\n", + "[ReadMore](https://pythonnumericalmethods.studentorg.berkeley.edu/notebooks/chapter22.00-ODE-Initial-Value-Problems.html)" + ], + "id": "508fb71a-8f30-4cb3-88f8-28b45a334596" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_3/notebook_3/ode.ipynb b/tutorials/module_3/notebook_3/ode.ipynb new file mode 100644 index 0000000..a343f4f --- /dev/null +++ b/tutorials/module_3/notebook_3/ode.ipynb @@ -0,0 +1,23 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Numerical Solutions of Ordinary Differential Equations\n", + "\n", + "## Euler’s Method\n", + "\n", + "### Forwards Eulers\n", + "\n", + "### Backwards Eulers\n", + "\n", + "## Runge-Kutta" + ], + "id": "4c1220ef-f6ce-43a7-9017-6c22fc8fd4af" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_3/notebook_3/roots_optimization.ipynb b/tutorials/module_3/notebook_3/roots_optimization.ipynb new file mode 100644 index 0000000..3e764f2 --- /dev/null +++ b/tutorials/module_3/notebook_3/roots_optimization.ipynb @@ -0,0 +1,25 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "metadata": {}, + "source": [ + "# Root Finding Methods\n", + "\n", + "Root Finding Methods or non-linear equation solvers.\n", + "\n", + "## Incremental Search\n", + "\n", + "## Bisection\n", + "\n", + "## Modified Secant\n", + "\n", + "## Newton-Raphson" + ], + "id": "9483ba01-3002-4544-9286-e134b3d2538b" + } + ], + "nbformat": 4, + "nbformat_minor": 5, + "metadata": {} +} diff --git a/tutorials/module_3/numerical_differentiation.ipynb b/tutorials/module_3/numerical_differentiation.ipynb new file mode 100644 index 0000000..f8091d0 --- /dev/null +++ b/tutorials/module_3/numerical_differentiation.ipynb @@ -0,0 +1,308 @@ +{ + "cells": [ + { + "cell_type": "markdown", + "id": "e74a8aaa-e960-4d76-a52e-24e7ead28023", + "metadata": {}, + "source": [ + "# Numerical Differentiation\n", + "We can find the derivate of both tabulated data and a continuous function using a finite difference method, which calculates rise over run of a function. To do this, we must first initalize our independant variable. Let's call this domain $x$ to be a vector such that $\\vec{x}$ =\n", + "$\\pmatrix{x_0, x_1, x_2, ...}$. This domain is also known as the **numerical grid**, is either determined by our data (often time) or can be set by us if it's a continuous function. The **step size** is defined as the spacing between adjacent points on the grid ($h = x_{i+1} - x_i$). Next, let's introduce the dependent variable $y$, this can be any function of $x$.\n", + "\n", + "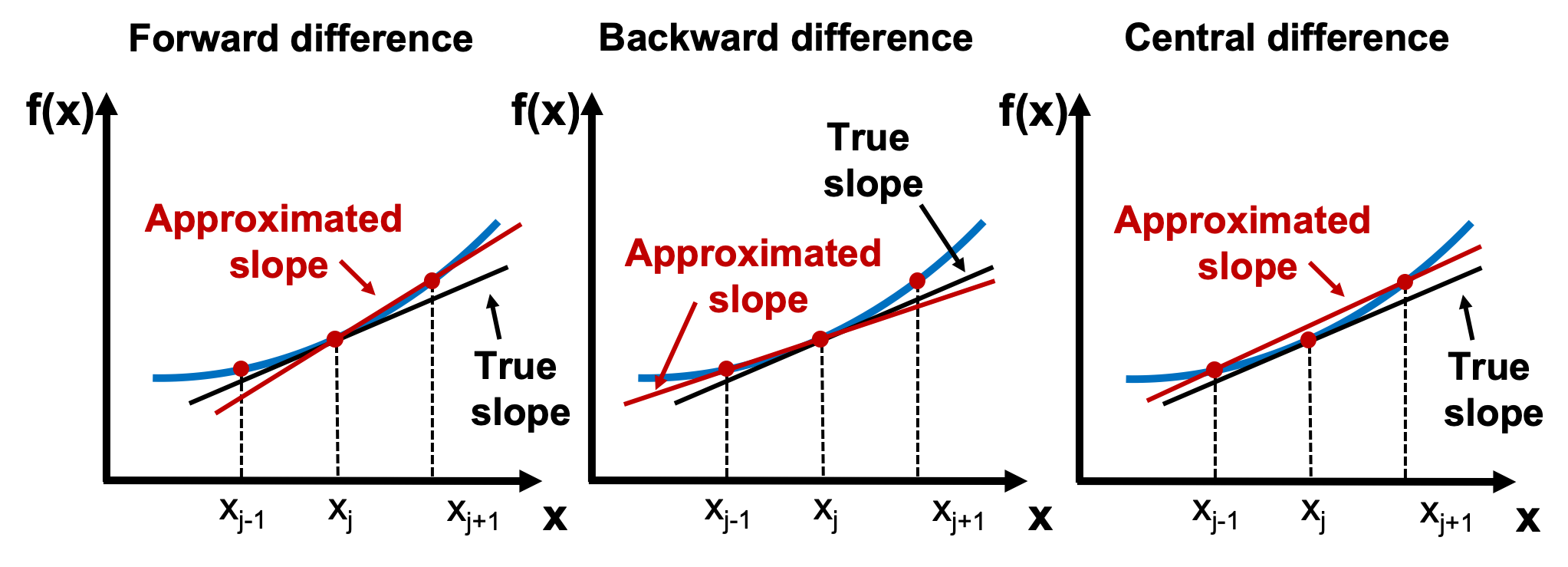\n", + "\n", + "For this tutorial let's model a falling object reaching terminal velocity using the equation below.\n", + "\n", + "$$ v(t) = 42.78 * (1 - e^{\\frac{-9.81*t}{42.78}}) $$\n", + "\n", + "Since we're starting with a continous function we can determine our step size ourselves, let's set it to `h=0.1`." + ] + }, + { + "cell_type": "code", + "execution_count": 1, + "id": "a97491b4-b183-4bdd-8c29-4cda0829d785", + "metadata": {}, + "outputs": [], + "source": [ + "import numpy as np\n", + "import matplotlib.pyplot as plt\n", + "\n", + "# Step size\n", + "h = 4\n", + "\n", + "# Initiate vectors\n", + "t = np.arange(0, 20, h) \n", + "v = 42.78 * (1 - np.exp(-9.81 * t / 42.78))\n" + ] + }, + { + "cell_type": "markdown", + "id": "9b79e5ba-4b71-4aeb-b3fb-878c2d728f7e", + "metadata": {}, + "source": [ + "## Forward Difference\n", + "The forward difference method takes the point at which we want to find the derivative and the point *forwards* on the grid.\n", + "\n", + "$$ f'(x_i) = \\frac{f(x_{i+1})-f(x_i)}{h} $$ \n", + "\n", + "Note that $f'$ will be 1 element shorter than $f$ due we are unable to take the derivative of the last element." + ] + }, + { + "cell_type": "code", + "execution_count": 2, + "id": "d2fe3ad1-8af0-499a-8954-41a88a49b834", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "[[ 0. 25.68442511 35.94833378 40.04995649 41.68903078]\n", + " [ 6.42110628 2.56597717 1.02540568 0.40976857 nan]]\n" + ] + } + ], + "source": [ + "# Forward difference method\n", + "dvdt = (v[1:] - v[:-1]) / h\n", + "\n", + "# Make a table of forward method\n", + "dvdt_fd = np.append(dvdt,np.nan)\n", + "table = np.vstack((v,dvdt_fd))\n", + "print(table)" + ] + }, + { + "attachments": {}, + "cell_type": "markdown", + "id": "4dfe5c25-f333-46bb-ab87-a7c97bb1e05f", + "metadata": {}, + "source": [ + "## Backwards Difference\n", + "\n", + "Uses the point at which we want to find the derivative and the *backward* point.$$\n", + "f'(x_i) = \\frac{f(x_{i})-f(x_{i-1})}{h}\n", + "$$\n", + "\n", + "Notice that this equation is essentially the same as the forwards difference formula. Let's think about it this way - the slope between each point will remain the same. However, since we're using the previous element to calculate the gradient, the enitre array will be shifted to the right. We can therefore use the same dvdt equation." + ] + }, + { + "cell_type": "code", + "execution_count": 3, + "id": "415d0b3c-a70d-48ef-93ad-6e827127b222", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "[[ 0. 25.68442511 35.94833378 40.04995649 41.68903078]\n", + " [ nan 6.42110628 2.56597717 1.02540568 0.40976857]]\n" + ] + } + ], + "source": [ + "dvdt = (v[1:] - v[:-1]) / h\n", + "\n", + "# Output results\n", + "dvdt_bd = np.insert(dvdt,0,np.nan)\n", + "table = np.vstack((v,dvdt_bd))\n", + "print(table)" + ] + }, + { + "cell_type": "markdown", + "id": "21c87595-add2-4f7a-8d10-2da3b4284e02", + "metadata": {}, + "source": [ + "## Central Difference\n", + "Combinging the two previous techniques we get the central difference. Here we average the two to slopes to get out slope.\n", + "$$\n", + "f'(x_i) = \\frac{f(x_{i+1})-f(x_{i-1})}{2h}\n", + "$$" + ] + }, + { + "cell_type": "code", + "execution_count": 4, + "id": "9d90ed83-d811-4394-b30b-ec80e7d835d4", + "metadata": {}, + "outputs": [ + { + "name": "stdout", + "output_type": "stream", + "text": [ + "[[ 0. 25.68442511 35.94833378 40.04995649 41.68903078]\n", + " [ nan 4.49354172 1.79569142 0.71758712 nan]]\n" + ] + } + ], + "source": [ + "dvdt_cd = (v[2:] - v[:-2]) / (2*h)\n", + "\n", + "# Output results\n", + "dvdt_cd = np.pad(dvdt_cd, (1, 1), mode='constant', constant_values=np.nan)\n", + "table = np.vstack((v,dvdt_cd))\n", + "print(table)" + ] + }, + { + "cell_type": "markdown", + "id": "213b1d8a-d92c-43f3-91d1-3c67711d0987", + "metadata": {}, + "source": [ + "## Visualization\n", + "Below we can plot $v(t)$ and $v'(t)$ using the methods above. Try decreasing step size and restart the kernel to see how `h` affects the derivative function." + ] + }, + { + "cell_type": "code", + "execution_count": 5, + "id": "e6a9f673-e9fc-457a-97b4-7e233f1fc280", + "metadata": {}, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxYAAAHqCAYAAACZcdjsAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAPYQAAD2EBqD+naQAAylJJREFUeJzs3XmcTfUfx/HXnX0f+8xYx77vFMoWY4sSKkuWkBZrsiRlzRIpKVSyVbYkErKGlCVLJIRk7GPJMmMw2z2/P85vbq4ZzHDHnRnv5+Mxj+793u8553O+947uZ76bxTAMAxERERERkfvg4uwAREREREQk41NiISIiIiIi902JhYiIiIiI3DclFiIiIiIict+UWIiIiIiIyH1TYiEiIiIiIvdNiYWIiIiIiNw3JRYiIiIiInLflFiIiIiIiMh9U2IhkgHMmjULi8WS7E+/fv1SfJ7w8HAsFguzZs1Kcu7w8HBbWadOnQgNDXXcDaSSYRjMnTuXJ554gqxZs+Lp6UmhQoXo3r07J06cSFK/Tp06lClTJkXntlgsDBs2zMER/2f06NEsWbIk1cdduHABT09PLBYLO3bscHxgGcSwYcOwWCxcuHDhrnVDQ0Pp1KlT2gd1k8T47vZTp06dBxrXrZL7vU4Ld3sP9uzZg8Vi4c0337xtncOHD2OxWOjVq1eKr5v4PqSV5M4/ZcoUu387RSQpN2cHICIpN3PmTEqUKGFXljt3bodf55133qF3794OP29KWK1W2rZty4IFC2jTpg2zZs0iMDCQP/74g/HjxzN37lyWLVvGY489dk/n37JlC3nz5nVw1P8ZPXo0rVq1onnz5qk67quvviI2NhaA6dOnU6VKlTSILnNZvHgxAQEBD/SaXbt2pVGjRrbnZ86coUWLFvTs2ZO2bdvayh90XLd68skn2bJlCyEhIU6No3z58lSuXJkvv/ySUaNG4erqmqTOzJkzAejSpcuDDu+2bn2fwUwscuTI8cCTWZGMRImFSAZSpkyZB/KFs3Dhwml+jdt57733WLBgAWPHjmXgwIG28jp16vD888/z6KOP0rJlS/766y+yZMmS6vNXq1bNgdE6zowZM8iVKxcFChRg3rx5fPDBB3h7ezsllmvXruHj4+OUa6dGxYoVH/g18+bNa5eYJvYI5M+f3yGfrevXr+Pl5XXff43PmTMnOXPmvO94HKFLly689tpr/PjjjzRt2tTutYSEBL788ksqV65M+fLlnRRhUre+zyKSMhoKJZIJ/P3337z44osULVoUHx8f8uTJQ7Nmzdi7d+89nS+5oVAWi4UePXrw1VdfUbJkSXx8fChfvjzLli1Lcvz3339PuXLlbEOYPvrooxQNXYiNjWX8+PGULFmSAQMGJHk9KCiIMWPGcPbsWaZPn57k9U2bNlGtWjW8vb3JkycP77zzDgkJCUnu49ahUBEREbz88svkzZsXDw8PChYsyPDhw4mPj7erFxMTw4gRIyhZsiReXl5kz56dunXrsnnzZtu5o6OjmT17dqqGxGzbto0///yT9u3b89JLL3HlyhUWLVqUpF7ikK+73WfikLdx48YxatQo8ufPj5eXF1WqVGHdunV250x8X3bt2kWrVq3ImjWrLbG8ceMGgwYNomDBgnh4eJAnTx66d+/O5cuX7c6xYMECGjRoQEhICN7e3pQsWZI333yT6OjoZO+1WbNmZM+eHS8vLwoXLkyfPn2S1Dt79ixt2rQhMDCQoKAgOnfuzJUrV+zq3DoMZ8OGDVgsFubNm8fgwYPJnTs3AQEB1K9fn4MHD9odaxgGo0ePpkCBAra2WbNmDXXq1HHIMKYdO3bw1FNPkS1bNry8vKhYsSLffPONXZ3E4UqrV6+mc+fO5MyZEx8fH2JiYmzv9ZYtW6hRowbe3t6Ehoba/rq/fPlyKlWqhI+PD2XLlmXlypXJnvvmoVCJ59y+fTs1a9bEx8eHQoUKMXbsWKxWq63ejRs3eOONN6hQoQKBgYFky5aN6tWr8/33399TW7Rt2xZvb29b7DdbvXo1p06donPnzrayBQsWUL16dXx9ffHz86Nhw4b8/vvvd72O1Wpl3LhxlChRAk9PT3LlykWHDh04efJkkrorV66kXr16BAYG4uPjQ8mSJRkzZozt9Vv/vQoNDWXfvn1s3LjR9rsdGhrK1atXyZIlCy+//HKSa4SHh+Pq6sr48ePvGrtIZqHEQiQDSUhIID4+3u4H4PTp02TPnp2xY8eycuVKJk+ejJubG48++miSL1T3Y/ny5XzyySeMGDGCRYsWkS1bNp555hn++ecfW52VK1fSokULsmfPzoIFCxg3bhzz5s1j9uzZdz3/zp07uXTpEk899dRtk5BmzZrh4uLCmjVr7MojIiJo3bo17dq14/vvv6dVq1a8++67dx3SFRERwSOPPMKqVasYMmQIP/74I126dGHMmDG89NJLtnrx8fE0btyYkSNH0rRpUxYvXsysWbOoUaMGx48fB8xhVt7e3jRp0oQtW7awZcsWpkyZctf7TkySOnfuTOvWrfHx8Uk2cUrtfX7yySesXLmSiRMn8vXXX+Pi4kLjxo3ZsmVLkrotWrSgSJEiLFy4kE8//RTDMGjevDnvv/8+7du3Z/ny5fTt25fZs2fzxBNPEBMTYzv28OHDNGnShOnTp7Ny5Ur69OnDN998Q7NmzeyusWrVKmrWrMnx48f54IMP+PHHH3n77bc5e/ZsknhatmxJsWLFWLRoEW+++SZz587l9ddfv2tbArz11lscO3aML774gs8//5zDhw/TrFkzu+Rr8ODBDB48mEaNGvH999/zyiuv0LVrVw4dOpSia9zJ+vXreeyxx7h8+TKffvop33//PRUqVOD5559Pdox+586dcXd356uvvuLbb7/F3d0dMN/rF198ka5du/L9999TtmxZOnfuzIgRIxg0aBADBgxg0aJF+Pn50bx5c06fPn3X2CIiImjXrh0vvPACS5cupXHjxgwaNIivv/7aVicmJoaLFy/Sr18/lixZwrx583j88cdp0aIFX375ZarbIzAwkJYtW/LDDz9w/vx5u9dmzpyJl5eXbRjZ6NGjadOmDaVKleKbb77hq6++Iioqipo1a7J///47XufVV19l4MCBhIWFsXTpUkaOHMnKlSupUaOG3Zyd6dOn06RJE6xWK59++ik//PADvXr1SjYBSbR48WIKFSpExYoVbb/bixcvxs/Pj86dOzNnzpwkie+UKVPw8PCwS5pEMj1DRNK9mTNnGkCyP3FxcUnqx8fHG7GxsUbRokWN119/3VZ+9OhRAzBmzpyZ5NxHjx61lXXs2NEoUKCA3TkBIygoyIiMjLSVRUREGC4uLsaYMWNsZVWrVjXy5ctnxMTE2MqioqKM7NmzG3f7J2f+/PkGYHz66ad3rBcUFGSULFnS9rx27doGYHz//fd29V566SXDxcXFOHbsmN19DB061Pb85ZdfNvz8/OzqGIZhvP/++wZg7Nu3zzAMw/jyyy8NwJg2bdodY/P19TU6dux4xzo3i46ONgICAoxq1arZyjp27GhYLBbj77//tqub0vtMfJ9z585tXL9+3VYvMjLSyJYtm1G/fn1b2dChQw3AGDJkiN05V65caQDGuHHj7MoXLFhgAMbnn3+e7P1YrVYjLi7O2LhxowEYe/bssb1WuHBho3DhwnYx3Soxnluv+9prrxleXl6G1Wq1lRUoUMCurdevX28ARpMmTeyO/eabbwzA2LJli2EYhnHx4kXD09PTeP755+3qbdmyxQCM2rVr3za+WyW29fjx421lJUqUMCpWrJjkd7Np06ZGSEiIkZCQYBjGf797HTp0SHLexPd6x44dtrJ///3XcHV1Nby9vY1Tp07Zynfv3m0AxqRJk2xlyf1eJ55z27ZtdtcqVaqU0bBhw9veY3x8vBEXF2d06dLFqFixot1rt74Ht5P43nzwwQd29+Pp6Wm0a9fOMAzDOH78uOHm5mb07NnT7tioqCgjODjYeO6552xliZ+TRAcOHDAA47XXXrM7dtu2bQZgvPXWW7ZzBQQEGI8//rjdZ+lWt57fMAyjdOnSyX42jhw5Yri4uBgffvihrez69etG9uzZjRdffPG21xDJjNRjIZKBfPnll2zfvt3ux83Njfj4eEaPHk2pUqXw8PDAzc0NDw8PDh8+zIEDBxx2/bp16+Lv7297HhQURK5cuTh27BgA0dHR7Nixg+bNm+Ph4WGr5+fnl+Sv1/fDMIwkPRr+/v489dRTdmVt27bFarXy888/3/Zcy5Yto27duuTOnduuJ6hx48YAbNy4EYAff/wRLy8vh//18ZtvviEyMtLuvJ07d8YwjGSHjqTmPlu0aIGXl5fdsc2aNePnn39OMkSsZcuWds9/+ukngCQTVZ999ll8fX3thlT9888/tG3bluDgYFxdXXF3d6d27doAts/foUOHOHLkCF26dLGL6XZuvcdy5cpx48YNzp07d0/HArbP6datW4mJieG5556zq1etWrX7Xg3t77//5q+//qJdu3YAdp+pJk2acObMmSS9iLe2faKQkBAqV65se54tWzZy5cpFhQoV7BZtKFmypN393UlwcDCPPPKIXVm5cuWSHLtw4UIee+wx/Pz8cHNzw93dnenTp9/zvye1a9emcOHCdp/pOXPmEBMTY/vsr1q1ivj4eDp06GDXbl5eXtSuXZsNGzbc9vzr168Hkn5eH3nkEUqWLGn7vG7evJnIyEhee+01h60qVahQIZo2bcqUKVMwDAOAuXPn8u+//9KjRw+HXEMko1BiIZKBlCxZkipVqtj9APTt25d33nmH5s2b88MPP7Bt2za2b99O+fLluX79usOunz179iRlnp6etmtcunQJwzAICgpKUi+5slvlz58fgKNHj962TnR0NBcuXCBfvnx3PX9wcDAA//77723Pd/bsWX744Qfc3d3tfkqXLg1gG0Jx/vx5cufOjYuLY//ZnD59Ol5eXjRq1IjLly9z+fJlypUrR2hoKLNmzUqSAKTmPhPLby2LjY3l6tWrduW3rh7077//4ubmlmQCsMViITg42Hatq1evUrNmTbZt28a7777Lhg0b2L59O9999x2A7bOROAQmpRNib/2seXp62p3vfo5NjP1eP6d3kjisq1+/fkk+U6+99hpAkqV0b7dyU7Zs2ZKUeXh4JClPTOJv3Lhx1/ju9jsM8N133/Hcc8+RJ08evv76a7Zs2cL27dvp3Llziq6RHIvFQufOndm7d69tOeWZM2dSsGBB6tatC/zXdlWrVk3SdgsWLLjjEsSJ72lybZk7d27b66n9HKZU7969OXz4sG2I5uTJk6levTqVKlVy6HVE0jutCiWSCXz99dd06NCB0aNH25VfuHDhnlZOuldZs2bFYrEkO2Y+IiLirsdXrlyZrFmzsnTpUsaMGZPsXxSXLl2K1WolLCzMrvxO10zuy1SiHDlyUK5cOUaNGpXs64l/Gc6ZMye//PILVqvVYcnFoUOH+OWXX4D/kqpbrVq1iiZNmtiep+Y+k2vziIgIPDw88PPzsyu/ta2zZ89OfHw858+ft0suDMMgIiKCqlWrAmbPxunTp9mwYYOtlwJIMsE78Rx3Gsf+oCS20+3a8n56LXLkyAHAoEGDaNGiRbJ1ihcvbvc8LfdjuBdff/01BQsWZMGCBXax3Tyv5l506tSJIUOGMGPGDNzd3fn9998ZOXKk7RqJbfftt99SoECBVJ078T09c+ZMkqTh9OnTtnOn1efwiSeeoEyZMnzyySf4+fmxa9cuu3krIg8L9ViIZAIWi8X2V9lEy5cv59SpUw80Dl9fX6pUqcKSJUtsezKA+Vft5FaPupWHhwf9+/fnwIEDya6kcu7cOQYNGkRQUBBdu3a1ey0qKoqlS5falc2dOxcXFxdq1ap122s2bdqUP//8k8KFCyfpDapSpYotsWjcuDE3bty46wZZt/71904SJ2hPmzaN9evX2/2sWLECd3d3ZsyYcc/3+d1339n9hTkqKooffviBmjVrJrufwM3q1asHkOTL0aJFi4iOjra9nvil8NbP32effWb3vFixYhQuXJgZM2bc9xfU+/Xoo4/i6enJggUL7Mq3bt2aouFEd1K8eHGKFi3Knj17kv08ValSxW44YXpksVjw8PCwSyoiIiLueVWoRLlz56ZRo0bMmzePyZMn4+LiQseOHW2vN2zYEDc3N44cOXLbtrudJ554Akj6ed2+fTsHDhywfV5r1KhBYGCgbYGC1Ljb73avXr1Yvny57d+oZ599NlXnF8kM1GMhkgk0bdqUWbNmUaJECcqVK8fOnTsZP368U9ZhHzFiBE8++SQNGzakd+/eJCQkMH78ePz8/Lh48eJdjx84cCB79uyx/ff555+32yAvKiqKZcuWERgYaHdc9uzZefXVVzl+/DjFihVjxYoVTJs2jVdfffW2vQGJ8a5Zs4YaNWrQq1cvihcvzo0bNwgPD2fFihV8+umn5M2blzZt2jBz5kxeeeUVDh48SN26dbFarWzbto2SJUvSunVrAMqWLcuGDRv44YcfCAkJwd/fP8lfqMEce//ll19SsmTJJElSombNmrF06VK7XoPU3KerqythYWH07dsXq9XKe++9R2RkJMOHD7/r+xAWFkbDhg0ZOHAgkZGRPPbYY/zxxx8MHTqUihUr0r59e8D8opY1a1ZeeeUVhg4diru7O3PmzGHPnj1Jzjl58mSaNWtGtWrVeP3118mfPz/Hjx9n1apVzJkz564xOUq2bNno27cvY8aMIWvWrDzzzDOcPHmS4cOHExISct89Up999hmNGzemYcOGdOrUiTx58nDx4kUOHDjArl27WLhwoYPuJG00bdqU7777jtdee41WrVpx4sQJRo4cSUhICIcPH76vc3fp0oXly5fzxRdf0LBhQ7shjaGhoYwYMYLBgwfzzz//0KhRI7JmzcrZs2f57bff8PX1ve1nt3jx4nTr1o2PP/7YtvpZeHg477zzDvny5bOtKObn58eECRPo2rUr9evX56WXXiIoKIi///6bPXv28Mknn9w29rJlyzJ//nwWLFhAoUKF8PLyomzZsrbXX3jhBQYNGsTPP//M22+/bTfPTOSh4cyZ4yKSMokrvGzfvj3Z1y9dumR06dLFyJUrl+Hj42M8/vjjxqZNm4zatWvbrWJyv6tCde/ePcm1k1sVZvHixUbZsmUNDw8PI3/+/MbYsWONXr16GVmzZk3R/VqtVmPOnDlGnTp1jCxZshgeHh5GwYIFjVdffTXJ6k2GYa52U7p0aWPDhg1GlSpVDE9PTyMkJMR46623kqzMAxjDhg2zKzt//rzRq1cvo2DBgoa7u7uRLVs2o3LlysbgwYONq1ev2updv37dGDJkiFG0aFHDw8PDyJ49u/HEE08YmzdvttXZvXu38dhjjxk+Pj53XGFoyZIlBmBMnDjxtu2QuDLThAkTUnWfie/ze++9ZwwfPtzImzev4eHhYVSsWNFYtWqV3TUSV785f/58kutfv37dGDhwoFGgQAHD3d3dCAkJMV599VXj0qVLdvU2b95sVK9e3fDx8TFy5sxpdO3a1di1a1eSz5phmCsvNW7c2AgMDDQ8PT2NwoUL261cdrt4kvuc3m5VqIULF9odm9zn3mq1Gu+++66tbcqVK2csW7bMKF++vPHMM88kaYvbSW5VKMMwjD179hjPPfeckStXLsPd3d0IDg42nnjiCbsVz+70e534Xt+qQIECxpNPPpmk/Nbfz9utCpXcOZP7fR87dqwRGhpqeHp6GiVLljSmTZuW7EpJKV0VKlFsbKwRFBRkAMY333yTbJ0lS5YYdevWNQICAgxPT0+jQIECRqtWrYy1a9fa6iQXS0JCgvHee+8ZxYoVM9zd3Y0cOXIYL7zwgnHixIkk11ixYoVRu3Ztw9fX1/Dx8TFKlSplvPfee3c8f3h4uNGgQQPD39/fAJK0mWEYRqdOnQw3Nzfj5MmTKW4TkczEYhip7AsUEUmluLg4KlSoQJ48eVi9erXT4rhy5QpZsmTh448/zpCrtdSpU4cLFy7w559/3rFeeHg4BQsWZPz48fTr1+8BRZfxHT16lBIlSjB06FDeeustZ4cjGUxsbCyhoaE8/vjjSTZDFHlYaCiUiDhcly5dCAsLIyQkhIiICD799FMOHDjARx995LSYtm7dahtTX716dafFIenDnj17mDdvHjVq1CAgIICDBw8ybtw4AgIC6NKli7PDkwzk/PnzHDx4kJkzZ3L27FnefPNNZ4ck4jRKLETE4aKioujXrx/nz5/H3d2dSpUqsWLFCurXr++0mNq2bUtCQgITJkyw2xtAHk6+vr7s2LGD6dOnc/nyZQIDA6lTpw6jRo267yVn5eGyfPlyXnzxRUJCQpgyZYqWmJWHmoZCiYiIiIjIfdNysyIiIiIict+UWIiIiIiIyH1TYiEiIiIiIvct00/etlqtnD59Gn9/f7tdREVERERE5M4MwyAqKorcuXPfdQPRTJ9YnD592m5nTxERERERSZ0TJ06QN2/eO9bJ9ImFv78/YDZGQECAU2KIi4tj9erVNGjQAHd3d6fEkBmoHR1D7egYakfHUVs6htrRMdSOjqF2dIz00I6RkZHky5fP9p36TjJ9YpE4/CkgIMCpiYWPjw8BAQH65boPakfHUDs6htrRcdSWjqF2dAy1o2OoHR0jPbVjSqYUaPK2iIiIiIjcNyUWIiIiIiJy35RYiIiIiIjIfcv0cyxSKiEhgbi4uDQ5d1xcHG5ubty4cYOEhIQ0ucbDQO3oGIntmJCQ4PTxmiIiIpJ5PPSJhWEYREREcPny5TS9RnBwMCdOnNBeGvdB7egYie34zz//kDVrVoKDg9WeIiIict8e+sQiManIlSsXPj4+afIFy2q1cvXqVfz8/O66sYjcntrRMaxWK1FRUbi4uHDhwgUAQkJCnByViIiIZHQPdWKRkJBgSyqyZ8+eZtexWq3Exsbi5eWlL8T3Qe3oGIntGBAQgIuLC+fOnSNXrly4uro6OzQRERHJwB7qb2eJcyp8fHycHImIcyR+9tNqfpGIiIg8PB7qxCKRxpfLw0qffREREXEUJRYiIiIiInLflFg8pEJDQ5k4cWK6Pd/NDh48SHBwMFFRUWly/uScO3eOnDlzcurUqQd2TREREZGMTIlFBtOsWTPq16+f7GtbtmzBYrGwa9euBxwVbN++nW7dutmeWywWlixZ4pBzDx48mO7du+Pv7++Q89WpU4dPP/30jnVy5cpF+/btGTp0qEOuKSIiIpLZKbHIYLp06cJPP/3EsWPHkrw2Y8YMKlSoQKVKlR54XDlz5kyTSfAnT55k6dKlvPjiiw4538WLF9m8eTPNmjW7a90XX3yROXPmcOnSJYdcW0RERCQzU2KRwTRt2pRcuXIxa9Ysu/Jr166xYMECunTpAsDmzZupVasW3t7e5MuXj169ehEdHX3b8x4/fpynn34aPz8/AgICeO655zh79qxdnaVLl1KlShW8vLzIkSMHLVq0sL1281Co0NBQAJ555hksFguhoaGEh4fj4uLCjh077M758ccfU6BAAQzDSDaub775hvLly5M3b15b2axZs8iSJQvLli2jePHi+Pj40KpVK6Kjo5k9ezahoaFkzZqVnj17Jtmhe/ny5ZQvX548efJw6dIl2rVrR86cOfH29qZo0aLMnDnTVrds2bIEBwezePHi27abiIiIiJiUWNzCMCA6+sH/3OZ7dRJubm506NCBWbNm2X0ZX7hwIbGxsbRr1469e/fSsGFDWrRowR9//MGCBQv45Zdf6NGjx23u2aB58+ZcvHiRjRs3smbNGo4cOcLzzz9vq7N8+XJatGjBk08+ye+//866deuoUqVKsufbvn07ADNnzuTMmTNs376d0NBQ6tevb/fFPbFOp06dbrs60c8//5zsda5du8akSZOYP38+K1euZMOGDbRo0YIVK1awYsUKvvrqKz7//HO+/fZbu+OWLl3K008/DcA777zD/v37+fHHHzlw4ABTp04lR44cdvUfeeQRNm3alGxsIiIiImkhLg7OnIHdu+H333Ny44azI0qZh3qDvORcuwZ+fo4+qwuQ5Y41rl4FX9+Una1z586MHz+eDRs2ULduXcAcBtWiRQuyZs1K7969adu2LX369AGgaNGiTJo0idq1azN16lS8vLzszrd27Vr++OMPjh49Sr58+QD46quvKF26NNu3b6dq1aqMGjWK1q1bM3z4cNtx5cuXTza+nDlzApAlSxaCg4Nt5V27duWVV17hgw8+wNPTkz179rB7926+++67295reHg4lStXTlIeFxfH1KlTKVy4MACtWrXiq6++4uzZs/j5+VGqVCnq1q3L+vXrbQlSTEwMq1atYsiQIYDZS1OxYkVb4pLY03KzPHny8Pvvv982PhEREZGUuHYNzp2Ds2fNn+QeJ/73338Tj3IHatCyZRxlyzox+BRSYpEBlShRgho1ajBjxgzq1q3LkSNH2LRpE6tXrwZg586d/P3338yZM8d2jGEYWK1Wjh49SsmSJe3Od+DAAfLly2dLKgBKlSpFlixZOHDgAFWrVmX37t289NJL9xV38+bN6dGjB4sXL6Z169a2+JP7Qp/o+vXrSRIhMDd2S0wqAIKCgggNDcXvpqwwKCiIc+fO2Z7/9NNPZM+enbL//8189dVXadmyJbt27aJBgwY0b96cGjVq2F3H29uba9eu3esti4iISCZlGHD5cvKJQXKPr15N3fldXCBnTgNv70hiYzPGZs5KLG7h45P6N/5urFYrkZGRBAQE4OKS/Oiz1M577tKlCz169GDy5MnMnDmTAgUKUK9ePdv1Xn75ZXr16pXkuPz58ycpMwwj2aFIN5d7e3unLsBkeHh40L59e2bOnEmLFi2YO3fuXZeozZEjR7KTp93d3e2eWyyWZMusVqvt+c3DoAAaN27MsWPHWL58OWvXrqVevXp0796d999/31bn4sWLth4YERERydzi4+HChZQnC3FxqTu/pycEBf33kyuX/X9vfpw9OyQkxLNixQbKlWuSNjfsYEosbmGxpHxIUkpZrZCQYJ73NnlFqj333HP07t2buXPnMnv2bF566SVbElCpUiX27dtHkSJFUnSuUqVKcfz4cU6cOGHrtdi/fz9Xrlyx9W6UK1eOdevWpXh1Jnd39yQTp8EcDlWmTBmmTJlCXFyc3QTw5FSsWJH9+/en6Jp3YhgGP/zwA19++aVdec6cOenUqROdOnWiZs2a9O/f3y6x+PPPP6lTp859X19ERESc48aNlA0/ShyClNJ5r4kCA5NPDJIr8/c3v2umVDJfpdI1JRYZlJ+fH88//zxvvfUWV65coVOnTrbXBg4cSLVq1ejevTsvvfQSvr6+HDhwgDVr1vDxxx8nOVf9+vUpV64c7dq1Y+LEicTHx/Paa69Ru3Zt2/yDoUOHUq9ePQoXLkzr1q2Jj4/nxx9/ZMCAAcnGFxoayrp163jsscfw9PQka9asAJQsWZJq1aoxcOBAOnfufNeekIYNG9K1a1cSEhJuO8E7JXbu3El0dDS1atWylQ0ZMoTKlStTunRpYmJiWLZsmd0wsWvXrrFz505Gjx59z9cVERERxzIMiIy8c7Jw8+PU7q9rsUDOnMknBrcmDrlyQTIjth9aSiwysC5dujB9+nQaNGhgN8SpXLlybNy4kcGDB1OzZk0Mw6Bw4cJ2qzzdLHEzu549e1KrVi1cXFxo1KiRXRJSp04dFi5cyMiRIxk7diwBAQF2X9JvNWHCBPr27cu0adPIkycP4eHhdnFv3ryZzp073/UemzRpgru7O2vXriUsLCwFrZK877//nieffBI3t/8+8h4eHgwaNIjw8HC8vb2pWbMm8+fPtzsmf/781KxZ856vKyIiIneXkGD2FqQkWTh3DmJiUnd+D4/bJwi3Jgs5coCra9rcZ2ZnMW63gUAmERkZSWBgIFeuXCEgIMDutRs3bnD06FEKFiyY7ARhR0nJHIuHyahRo5g/fz579+5NUf0pU6bw/fff8+OPP95zO5YrV463336b5557LsXHPPLII/Tp04e2bdum6lrp3c2fx9jY2AfyO5AZxcXFsWLFClvyK/dObekYakfHUDs6RlxcHN9/v5KKFRtx6ZL7XZOFCxfMoeOp4e+f8mQhMDB1Q5DSi/TwebzTd+lbqcdCHpirV69y4MABPv74Y0aOHJni47p168alS5eISm1f5v/FxsbSsmVLGjdunOJjzp07R6tWrWjTps09XVNERCSzMQxzWFFK5iqcO+fGlSvNUnV+i8WcsJzSZMEB68qIgymxkAemR48ezJs3j+bNm6doGFQiNzc3Bg8ebPtLe2p5eHgwdOjQVB2TK1eu284fERERySys1v+GIN09WSAVG7WZ3QPu7ga5cllSlCzkyAFu+maaoentkwdm1qxZzJo1y9lhiIiIZGqxsSlbKvXsWTh/PvVDkPz87rzyUVAQZM0axx9/rOHZZ8Pw8NCQsoeFEgsRERGRdMwwzD22UposXL6c+mtkz373ZCFxFaSULMsfFwf//BOXIec1yL1LN4nFmDFjeOutt+jdu7dt0zTDMBg+fDiff/45ly5d4tFHH2Xy5MmULl3aucGKiIiI3AerFS5eTHmycP166s7v5vZfInC3/RVy5gTNUxdHSBeJxfbt2/n8888pV66cXfm4ceP44IMPmDVrFsWKFePdd98lLCyMgwcP4u/v76RoRURERJKKi/tvOdS7zVU4f97c5Tk1fHzuPJn55rKsWR23Ka9ISjk9sbh69Srt2rVj2rRpvPvuu7ZywzCYOHEigwcPtu3OPHv2bIKCgpg7dy4vv/yys0IWERGRh0R0dMonNl+8mPrzZ82a8mTBz8/x9yfiSE5PLLp3786TTz5J/fr17RKLo0ePEhERQYMGDWxlnp6e1K5dm82bNyuxEBEREYe4cQN27YKtW2HLFlf27q3J66+7ce6cmVikhqurObQoJclCzpzmxm0imYVTE4v58+eza9cutm/fnuS1iIgIAIKCguzKg4KCOHbs2G3PGRMTQ8xN2zEmLk8aFxdHXFycXd24uDgMw8BqtWJN7ZIIqZC4B2HiteTeqB0d49Z2NAyDuLg4XLXNaKok/nty678rknpqS8dQO6aMYcDx47Btm4Vt2yxs3Wph924LcXGJs4xdgGx2x3h5Gf9PCoybkgbj/3MYjP8nCeZ/s2VL3RCkzPp26fPoGOmhHVNzbaclFidOnKB3796sXr36jjv+Wm5ZTsAwjCRlNxszZgzDhw9PUr569Wp8fHzsytzc3AgODubq1avExsam8g5S7143eMvsxo4dy/Lly9m0aVOK6kdFRfHLL7/QrFkzwsPDCQwMZO7cuQwaNMgu6Zw1axbjx4/nzJkzjBo1ildffTXZsodVVFQUsbGxXL9+nZ9//pn41A72FQDWrFnj7BAyDbWlY6gd7cXEuHDkSBYOHszGwYNZOXgwG5cuJf3eERgYQ/HiFylW7BJ5814lS5YbBAbGkiVLDF5e8Xdc3ejaNTh2zPwRe/o8OoYz2/HatWsprmsxEv98+YAtWbKEZ555xu6vpAkJCVgsFlxcXDh48CBFihRh165dVKxY0Vbn6aefJkuWLMyePTvZ8ybXY5EvXz4uXLiQZBvyGzducOLECUJDQ++Y3NwvwzCIiorC39//jklRSr344ot8+eWXScoT2yyjGT58ON9//z27du26Y72b23Hjxo3Uq1ePf//9lyxZsnD9+nWioqLIlSsXYL7vuXLlYsKECbRo0YLAwEDi4+OTlN2abD4Mbm7HmJgYwsPDyZcvX5r+DmRGcXFxrFmzhrCwMNy1nMp9UVs6htrR7I0ID4etWy389pvZG7Fnj4X4ePv/97q5GZQrZ1CtmsEjj5j/LVjQ3PlZ7egYakfHSA/tGBkZSY4cObhy5UqS79K3clqPRb169di7d69d2YsvvkiJEiUYOHAghQoVIjg4mDVr1tgSi9jYWDZu3Mh777132/N6enri6emZpNzd3T3JG3JzIuOShksnJA7bSbzW/bJYLDRq1IiZM2falefMmfOezh8bG4vHAxjkGRcXl+wvRWKydbfYk2vHxPfO19cX35sW1j558iRxcXE0bdqUPHnyAPDnn38mKXPkfWQUt7ajxWJJ9vdDUkZt5zhqS8d4mNoxOhp27EicG2H+9+zZpPWCg6F6dahWzfxv5coWfHzu/Ie+h6kd05La0TGc2Y6pua7TFiLz9/enTJkydj++vr5kz56dMmXKYLFY6NOnD6NHj2bx4sX8+eefdOrUCR8fH9q2beussNMNT09PgoOD7X4Se382btzII488gqenJyEhIbz55pt2w1zq1KlDjx496Nu3Lzly5CAsLIw33niDZs2a2epMnDgRi8XC8uXLbWXFixfns88+A8wlgsPCwsiRIweBgYHUrl07SY+DxWLh008/5emnn8bX19c2OX/s2LEEBQXh7+9Ply5duHHjxl3vd8WKFZQoUYKQkBDq1atHeHi43euzZs0iS5Ystsdly5YFoFChQlgslmTLEs/xww8/ULlyZby8vChUqBDDhw+3a6/b3UdKjvviiy945pln8PHxoWjRoixdutQu7n379vHkk08SEBCAv78/NWvW5MiRI7bXZ86cScmSJfHy8qJEiRJMmTLlrm0lIpIZGQYcOQJffw3du0PlyhAYCHXqwJtvwvffm0mFmxtUrQq9esG8eXD0KJw+Dd99BwMGQM2a5rKtIuJ4Tl8V6k4GDBjA9evXee2112wb5K1evTpN97AwDIPrcQkOPafVauV6bAJusfG3/au8t7urQ4ZJnTp1iiZNmtCpUye+/PJL/vrrL1566SW8vLwYNmyYrd7s2bN59dVX+fXXXzEMg8OHDzN9+nSsVisuLi5s3LiRHDlysHHjRp588kkiIiI4dOgQtWvXBszx+R07dmTSpEkATJgwgSZNmnD48GG792fo0KGMGTOGDz/8EFdXV7755huGDh3K5MmTqVmzJl999RWTJk2iUKFCt72nEydO0KJFC15++WVeeOEF/vrrL/r373/b+s8//zz58uWjfv36/Pbbb+TLlw9/f/8kZTlz5mTVqlW88MILTJo0yfalvlu3brbYb3cfKT1u+PDhjBs3jvHjx/Pxxx/Trl07jh07RrZs2Th16hS1atWiTp06/PTTTwQEBPDrr7/akpNp06YxdOhQPvnkEypWrMjvv//OSy+9hK+vLx07dkzpR0JEJEO6ehW2b/+vJ2LrVnPvh1vlzm3fG1GpEnh7P/h4RSSdJRYbNmywe26xWBg2bJjdF+K0dj0ugVJDVj2w6yXaP6IhPh4pfzuWLVuG300LWjdu3JiFCxcyZcoU8uXLxyeffILFYqFEiRKcPn2agQMHMmTIEFtiU6RIEcaNG2c7PiQkhKioKH7//XcqVarEpk2b6NevH9999x0A69evJygoiBIlSgDwxBNP2MXz2WefkTVrVjZu3EjTpk1t5W3btqVz5862523atKFz58507doVgHfffZe1a9fesddi6tSpFCpUiA8++ICoqCgqV67Mvn37bjskztvbm+zZswPm8LDg4GCAZMtGjRrFm2++afuiXqhQIUaOHMmAAQPsEoRb76N9+/YpOq5Tp060adMGgNGjR/Pxxx/z22+/0ahRIyZPnkxgYCDz58+3dTMWK1bMduzIkSNt80EAChYsyP79+/nss8+UWIhIpmIYcPjwf0OatmyBvXvN3alv5uFhJg6JSUT16pA3L3ecWC0iD066Siwk5erWrcvUqVNtzxPnFxw4cIDq1avb9X489thjXL16lZMnT5I/f34AqlSpYne+wMBAKlSowIYNG3B3d8fFxYWXX36ZoUOHEhUVxYYNG2y9FQDnzp1jyJAh/PTTT5w9e5aEhASuXbvG8ePH7c5763UOHDjAK6+8YldWvXp11q9ff9t7PXDgANWqVbO7p+rVq9+xfVJq586dbN++nVGjRtnKEhISuHHjBteuXbNN7r71PlJ63M27yfv6+uLv78+5c+cA2L17NzVr1kx27OL58+c5ceIEXbp04aWXXrKVx8fHExgY6IA7FxFxnsjIpL0R//6btF6+fPZJRMWKkMw0ShFJJ5RY3MLb3ZX9Ixo69JxWq5WoyCj8A/zvOBQqNXx9fZNdASq55XgTF/66ufzmic6J6tSpw4YNG/Dw8KB27dpkzZqV0qVL8+uvv7Jhwwb69Oljq9upUyfOnz/PxIkTKVCgAJ6enlSvXj3Jsr3JXSe10nLhMqvVyvDhw229Aje7eZWkW+8jpcfdmjRYLBbb5GnvO/TVJ9aZNm0ajz76qN1r2m9CRDISqxUOHfovidiyBf780+yluJmnpzlv4uZhTfexzoaIOIESi1tYLJZUDUlKCavVSryHKz4ebmm6+hRAqVKlWLRokV2CsXnzZvz9/e+6ElKdOnWYPn06bm5u1K9fH4DatWszf/58u/kVAJs2bWLKlCk0adIEMOdBXLhw4a7xlSxZkq1bt9KhQwdb2datW+96T0uWLLEru9sxKVWpUqV7Wqb3Xo+7Wbly5Zg9e3ayq0wFBQWRJ08e/vnnH9q1a3fP1xARedCuXIFt2/5LIrZtg0uXktYrUMC+N6JCBe1CLZLRKbHIZF577TUmTpxIz5496dGjBwcPHmTo0KH07dv3rklNrVq1iIqK4ocffrCtfFSnTh1atmxJzpw5KVWqlK1ukSJF+Oqrr6hSpQqRkZH079//jn+BT9S7d286duxIlSpVePzxx5kzZw779u274+TtV155hQkTJvDGG2/Qtm1bDh48yKxZs1LWIHcxZMgQmjZtSr58+Xj22WdxcXHhjz/+YO/evbY2cORxN+vRowcff/wxrVu3ZtCgQQQGBrJ161YeeeQRihcvzrBhw+jVqxcBAQE0btyYmJgYduzYwaVLl+jbt69D7l9E5H5YrfDXX//Ni9i6FfbvT9ob4eUFVar8l0RUqwYhIc6JWUTSjhKLTCZPnjysWLGC/v37U758ebJly0aXLl14++2373psYGAgFStW5Pjx47YkombNmlitVrveCoAZM2bQrVs3KlasSP78+Rk9ejT9+vW76zWef/55jhw5wsCBA7lx4wYtW7bk1VdfZdWq20+Yz58/P4sWLeL1119n6tSpPPLII4wePdpuMvW9atiwIcuWLWPEiBGMGzcOd3d3SpQoYZtc7ujjbpY9e3Z++ukn+vfvT+3atXF1daVChQo89thjAHTt2hUfHx/Gjx/PgAED8PX1pWzZsnZD0kREHqRLl5L2Rly5krRewYL2SUT58qCtDEQyP6ftvP2gREZGEhgYmOxugTdu3ODo0aMULFgwTXcdtlqtREZGEhAQkOZDoTIztaNj3NyOsbGxD+R3IDOKi4tjxYoVNGnSRJs/3Se1pWM4uh0TEszeh5tXavrrr6T1fHzMfSMShzVVqwZBQfd9eafR59Ex1I6OkR7a8U7fpW+lHgsRERHh33/NHojEJOK33yAqKmm9woXteyPKlTM3pRMR0T8FIiIiD5mEBHNlpptXajp0KGk9X1945JH/kohq1SBnzgcfr4hkDEosREREMrnz55P2RkRHJ61XrJj9cq+lS6s3QkRSTv9ciIiIZCLx8f/1RiT2SPz9d9J6/v7/9UZUrw6PPgrZsz/4eEUk81BiISIikoGdO2cmEL/84sKPPz5G27ZuXLuWtF6JEva9EaVKgfbbFBFHUmIhIiKSQcTFwZ499is1HT2a+KorkAOAwECzByIxiXj0Ucia1VlRi8jDQomFiIhIOhURYT+kaccOuH7dvo7FYvY+PPKIFR+fPXTtWoZy5dzRqtwi8qApsRAREUkHYmNh9277lZqOHUtaL0sW+z0jHnnELIuLS2DFiuOULl1GSYWIOIUSCxERESc4dco+idi5E2Ji7OtYLFCmzH+JRPXq5spNShxEJD3SP01yW6GhoUycONHZYSSxYcMGLBYLly9fTtVxFouFJUuWABAeHo7FYmH37t2213/99VfKli2Lu7s7zZs3v22ZiEhqxcSYCcSHH8Jzz0H+/JA3Lzz7LEyYAJs3m3WyZYMmTWDkSFi7Fi5fhj/+gM8/hxdfNCdgK6kQkfRKPRYZUKdOnZg9e7btebZs2ahatSrjxo2jXLlyTows48iXLx9nzpwhR44ctrK+fftSoUIFfvzxR/z8/G5bJiJyJ4YBJ0/az43Ytcsc6nQzFxcoW9Z+paaiRc1eChGRjEiJRQbVqFEjZs6cCUBERARvv/02TZs25fjx406OzHFiY2Px8PBIk3O7uroSHBxsV3bkyBFeeeUV8ubNe8ey1ErL+xAR57txwxzGdPNKTadPJ62XI4d9ElG1KujvFSKSmahDNYPy9PQkODiY4OBgKlSowMCBAzlx4gTnz5+31Rk4cCDFihXDx8eHQoUK8c477xAXF2d3nqVLl1KlShW8vLzIkSMHLVq0uO01Z86cSWBgIGvWrOGHH34gS5YsWK1WAHbv3o3FYqF///62+i+//DJt2rQB4N9//6VNmzbkzZsXHx8fypYty7x58+zOX6dOHXr06EHfvn3JkSMHYWFhAKxYsYJixYrh6+tLs2bNCA8Pv2v7HD58mFq1auHl5UWpUqVYs2aN3es3D4VKfPzvv//SuXNnLBYLs2bNSrYMYP/+/TRp0gQ/Pz+CgoJo3749Fy5cuOt9pOS4Xr16MWDAALJly0ZwcDDDhg2zi/vy5ct069aNoKAgvLy8KFOmDMuWLbO9vnnzZmrVqoW3tzf58uWjV69eRCe3va6I3BPDgPBwmD8fevc2J04HBMDjj0O/frBokZlUuLpCxYrw2mvw1Vdw+LC538TSpfDWW1C3rpIKEcl8lFjcyjAgNtrxP3HX7vy6YdxzyFevXmXOnDkUKVKE7Ddtm+rv78+sWbPYv38/H330EdOmTePDDz+0vb58+XJatGjBk08+ye+//866deuoUqVKstd4//336devH6tWrSIsLIxatWoRFRXF77//DsDGjRvJkSMHGzdutB2zYcMGateuDcCNGzeoXLkyy5Yt488//6Rbt260b9+ebdu22V1n9uzZuLm58euvv/LZZ59x4sQJWrRoQZMmTdi1axft27fnrbfeumN7WK1WWrRogaurK1u3buXTTz9l4MCBt62fOCwqICCAiRMncubMGZ599tkkZc8//zxnzpyhdu3aVKhQgR07drBy5UrOnj3Lc889d8f7SM1xvr6+bNu2jXHjxjFixAhbUmS1WmncuDGbN2/m66+/Zv/+/YwdOxbX/+9wtXfvXho2bEiLFi34448/WLBgAb/88gs9evS4Y3uJyO1dvw6bNsG4cdCiBeTODQULQps2MGkSbN9u7i2RKxc8/TSMHQsbNsCVK+bwp8mT4YUXoEgRDXESkcxPQ6FuFXcNRud26CldgCx3q/TWafDwTfE5ly1bZhvzHx0dTUhICMuWLcPlpll9b7/9tu1xaGgob7zxBgsWLGDAgAEAjBo1itatWzN8+HBbvfLlyye51qBBg5g9ezYbNmygbNmyAAQGBlKhQgU2bNhA5cqV2bBhA6+//jrDhw8nKiqK6OhoDh06RJ06dQDIkycP/fr1s52zZ8+erFy5koULF/Loo4/ayosUKcK4ceP+a5a33qJQoUJ8+OGHGIZBSEgIR44csatzq7Vr13LgwAHCw8NtQ5hGjx5N48aNk62fOCzKYrEQGBhoGyLl6+ubpGzMmDFUqlSJ0aNH246fMWMG+fLl49ChQxQrVizZ+xgyZEiKjitXrhxDhw4FoGjRonzyySesW7eOsLAw1q5dy2+//caBAwds9QsVKmQ73/jx42nbti19+vSxHT9p0iRq167N1KlT8fLyum2biYj5952jR+1XatqzB+Lj7eu5uUGFCvYrNYWGKnEQEVFikUHVrVuXqVOnAnDx4kWmTJlC48aN+e233yhQoAAA3377LRMnTuTvv//m6tWrxMfHExAQYDvH7t27eemll+54nQkTJhAdHc2OHTvsvsSCOXRnw4YN9O3bl02bNvHuu++yaNEifvnlFy5fvkxQUBAlSpQAICEhgbFjx7JgwQJOnTpFTEwMMTEx+PraJ1O39pgcOHCAatWqYbFYMP7fq1OtWrU7xnzgwAHy589vNy+ievXqdzwmpXbu3Mn69euTnch95MgR2xf+W+8jpcfdOvk+JCSEc+fOAeb7lTdvXlvd5GL7+++/mTNnjq3MMAysVitHjx6lZMmSqbhTkcwvOtrccO7mSdb//3WzExz8XwJRvTpUqgQ+Pg8+XhGR9E6Jxa3cfczeAweyWq1ERkUR4O9v16OQ5Lqp4OvrS5EiRWzPK1euTGBgINOmTePdd99l69attt6Ihg0bEhgYyPz585kwYYLtGG9v77tep2bNmixfvpxvvvmGN9980+61OnXqMH36dPbs2YOLiwulSpWidu3abNy4kUuXLtmGQYGZoHz44YdMnDiRsmXL4uvrS58+fYi9ZZmUWxMN4x6GiCV3jMVBf0q0Wq00a9aM9957L8lrISEhtse33kdKj3N3d7d7zWKx2Oax3O39slqtvPzyy/Tq1SvJa/nz57/jsSKZnWHAkSP2ScQff0BCgn09d3dzbsTNk6zz51dvhIhISiixuJXFkqohSSlitYJ7gnneNFqA3GKx4OLiwvXr1wFz/4UCBQowePBgW51jt2zhWq5cOdatW8eLL7542/M+8sgj9OzZk4YNG+Lq6mo3OTtxnsXEiROpXbs2FouF2rVrM2bMGC5dukTv3r1tdTdt2sTTTz/NCy+8AJhfgg8fPnzXv6KXKlXKtvdEolvnZSR3zPHjxzl9+jS5c5vD2rZs2XLHY1KqUqVKLFq0iNDQUNzcUv7rc6/H3axcuXKcPHnSbujUrdfYt2+fXcIp8rC6ehV+++2/IU1bt8JNayXY5Mljn0RUqgQaNSgicm80eTuDiomJISIigoiICA4cOEDPnj25evUqzZo1A8wx/sePH2f+/PkcOXKESZMmsXjxYrtzDB06lHnz5jF06FAOHDjA3r17k527UL16dX788UdGjBhhN/k7cZ7F119/bZtLUatWLXbt2mU3vyIxnjVr1rB582YOHDjAyy+/TERExF3v85VXXuHIkSP07duXgwcPsnDhQrs9PJJTv359ihcvTocOHdizZw+bNm2yS7DuR/fu3bl48SJt2rTht99+459//mH16tV07tyZhFv/9OmA425Wu3ZtatWqRcuWLVmzZg1Hjx7lxx9/ZOXKlYC5CtiWLVvo3r07u3fv5vDhwyxdupSePXs65N5F0ivDgIMHYfZseOUVc/5DYCDUqweDB8OyZWZS4eFhJhCvvw7ffAPHj5v7TSxcCG+8ATVqKKkQEbkfSiwyqJUrVxISEkJISAiPPvoo27dvZ+HChbYv808//TSvv/46PXr0oEKFCmzevJl33nnH7hx16tRh4cKFLF26lAoVKvDEE0/ctjfgscceY/ny5bzzzjtMmjTJVl63bl0SEhJs182aNSulSpUiZ86cdr0R77zzDpUqVaJhw4bUqVOH4ODgFO1knT9/fhYtWsQPP/xAxYoVmTlzJu++++4dj3FxcWHx4sXExMTwyCOP0LVrV0aNGnXXa6VE7ty5+fXXX0lISKBhw4aUKVOG3r17ExgYePthbvdx3K0WLVpE1apVadOmDaVKlWLAgAG2xKRcuXJs3LiRw4cPU7NmTSpWrMg777xjN9RKJDOIjDR3pR45Ep580twfokQJ6NQJPvvMnHBttUK+fOYu1x9+aPZaREaa//3gA3PH63z5nH0nIiKZi8W4l0HsGUhkZCSBgYFcuXLFbuIymEugHj16lIIFC6bpijlWq5XIyEgCAgJS9SVS7KkdHePmdoyNjX0gvwOZUVxcHCtWrKBJkyZJ5sZI6typLa1Wszfi5pWa9u1LukK3pydUqfLfkKZq1cxhTg8TfSYdQ+3oGGpHx0gP7Xin79K30hwLERFJNy5fNudGJE6y3rbNLLtVaKh9ElGhgjnUSUREnEeJhYiIOM3VqzBvnoUFCyowaJAbf/2VtDfC29vsjUhMIqpVA43wExFJf5RYiIjIAxcfDzNmwJAhcPasG1DA9lqhQvYrNZUrZy4DKyIi6ZsSCxEReWAMA1asgP794cABs6xwYYMKFQ7Ttm0hHnvMjaAg58YoIiL3RjNgRUTkgfj9d6hfH5o2NZOKbNngo49gz5542rc/QLNmhpIKEZEMTD0WIiKSpk6cMPeT+Pprs8fC0xN694ZBgyBLFoiLc3aEIiLiCEosREQkTURGwtix5j4SN26YZW3bwqhR5qpOIiKSuSixEBERh4qLg88/h+HD4fx5s6x2bXj/fXN1JxERyZyUWIiIiEMYBixdCgMGwKFDZlnx4jBuHDRrBhaLc+MTEZG0pcnb8kCFhoYyceLEVB3TqVMnmjdvbnv+xBNP0KdPH9vza9eu0bJlSwICArBYLFy+fDnZMhFJO7/9ZvZKNG9uJhU5c8KUKbB3Lzz1lJIKEZGHgRKLDCoiIoKePXtSqFAhPD09yZcvH82aNWPdunUOvU6dOnXsvsSnB99++y0jR460PZ89ezabNm1i8+bNnDlzhsDAwGTLRMTxwsPNeROPPgqbNoGXF7z1Fvz9N7z6qvafEBF5mGgoVAYUHh7OY489RpYsWRg3bhzlypUjLi6OVatW0b17d/76668HGo9hGCQkJODm9mA+TtmyZcPF5b+c+MiRI5QsWZIyZcrcsSy1EhISsFgsdtcSEdOlSzB6NEyaBLGxZo9Ehw4wciTky+fs6ERExBn0jSkDeu2117BYLPz222+0atWKYsWKUbp0afr27cvWrVtt9a5cuUK3bt3IlSsXAQEBPPHEE+zZs8f2+rBhw6hQoQJfffUVoaGhBAYG0rp1a6KiogBzCNLGjRv56KOPsFgsWCwWwsPD2bBhAxaLhVWrVlGlShU8PT3ZtGkTR44c4emnnyYoKAg/Pz+qVq3K2rVrU3VvCQkJ9O3blyxZspA9e3YGDBiAYRh2dW4eClWnTh0mTJjAzz//jMVioU6dOsmWAcTGxjJgwADy5MmDr68vjz76KBs2bLCdd9asWWTJkoVly5ZRqlQpPD09OXbsWIqPW7VqFSVLlsTPz49GjRpx5swZu7hnzJhB6dKl8fT0JCQkhB49eqT4vRJJL2Jjzb0nihQxJ2PHxkK9erBrF8yapaRCRORhpsTiFoZhcC3umsN/rsdfv+Prt355vp2LFy+ycuVKunfvjq+vb5LXs2TJYruPJ598koiICFasWMHOnTupVKkS9erV4+LFi7b6R44cYcmSJSxbtoxly5axceNGxo4dC8BHH31E9erVeemllzhz5gxnzpwh303fGgYMGMCYMWM4cOAA5cqV4+rVqzRp0oS1a9fy+++/07BhQ5o1a8bx48dT3P4TJkxgxowZTJ8+nV9++YWLFy+yePHi29b/7rvveOmll6hevTpnzpzhu+++S7YM4MUXX+TXX39l/vz5/PHHHzz77LM0atSIw4cP28537do1xowZwxdffMG+ffvIlStXio97//33+eqrr/j55585fvw4/fr1s70+depUunfvTrdu3di7dy9Lly6lSJEiqXqvRJzJMODbb6FUKejTBy5ehNKlzV2016yBChWcHaGIiDibhkLd4nr8dR6d++gDv+62ttvwcfe5a72///4bwzAoUaLEHeutX7+evXv3cu7cOTw9PQF4//33WbJkCd9++y3dunUDwGq1MmvWLPz9/QFo374969atY9SoUQQGBuLh4YGPjw/BwcFJrjFixAjCwsJsz7Nnz0758uVtz999910WL17M0qVL7f46fycTJ05k0KBBtGzZEoBPP/2UVatW3bZ+tmzZ8PHxwcPDwy7GW8uOHDnCvHnzOHnyJLlz5wagX79+rFy5kpkzZzJ69GgA4uLimDJliu0+UnPcp59+SuHChQHo0aMHI0aMsGuLN954g969e9vKqlatCqT8vRJxli1b4I03zP8CBAebQ546dYIHNAJSREQyAP0vIYNJ7Nmw3GWJlZ07d3L16lWyZ89uV379+nWOHDliex4aGmpLKgBCQkI4d+5cimKpcsuC9NHR0QwfPpxly5Zx+vRp4uPjuX79eop7LK5cucKZM2eoXr26rczNzY0qVaqkuEfndnbt2oVhGBQrVsyuPCYmxq6NPDw8KFeuXKqP8/HxsSUVYN+O586d4/Tp09SrVy/Z2FL6Xok8aEeOwJtvmj0VAD4+0L8/9OsHfn7OjU1ERNIfJRa38HbzZlvbbQ49p9VqJSoqCn9//9tOBPZ2807RuYoWLYrFYuHAgQN2S7Amd82QkBC7uQCJEodLAbjfsmSLxWLBarWmKJZbh2L179+fVatW8f7771OkSBG8vb1p1aoVsbGxKTpfWrJarbi6urJz505cXV3tXvO76RuSt7e3XdKW0uOSa8fEZMjb+87vbUrfK5EH5d9/4d13YfJkc7M7Fxd48UUYMQL+33EnIiKShBKLW1gslhQNSUoNq9VKvFs8Pu4+973CULZs2WjYsCGTJ0+mV69eSb7cX758mSxZslCpUiUiIiJwc3MjNDT0nq/n4eFBQkJCiupu2rSJTp068cwzzwBw9epVwsPDU3ytwMBAQkJC2Lp1K7Vq1QIgPj7eNufgflSsWJGEhATOnTtHzZo10/y4m/n7+xMaGsq6deuoW7duktcd9V6J3K8bN+CTT8yk4soVs6xRI3ODu7JlnRubiIikf5q8nQFNmTKFhIQEHnnkERYtWsThw4c5cOAAkyZNsg0jql+/PtWrV6d58+asWrWK8PBwNm/ezNtvv82OHTtSfK3Q0FC2bdtGeHg4Fy5cuGNvRpEiRfjuu+/YvXs3e/bsoW3btinu/UjUu3dvxo4dy+LFi/nrr7947bXXHLK5XbFixWjXrh0dOnTgu+++4+jRo2zfvp333nuPFStWOPy4Ww0bNowJEyYwadIkDh8+zK5du/j4448Bx71XIvfKaoV586BkSXOo05UrUK4crF4NP/6opEJERFJGiUUGVLBgQXbt2kXdunV54403KFOmDGFhYaxbt46pU6cCZs/LihUrqFWrFp07d6ZYsWK0bt2a8PBwgoKCUnytfv364erqSqlSpciZM+cd50t8+OGHZM2alRo1atCsWTMaNmyY6p6GN954gw4dOtCpUyeqV6+Ov7+/rQfkfs2cOZMOHTrwxhtvULx4cZ566im2bdtmt9KVI4+7WceOHZk4cSJTpkyhdOnSNG3a1LaqlKPeK5F78fPPUK2aucldeLg51GnmTHP52JvWZhAREbkri3G/s2LTucjISAIDA7ly5QoBAQF2r924cYOjR49SsGBBvLy80iwGq9VKZGQkAQEB2mztPqgdHePmdoyNjX0gvwOZUVxcHCtWrKBJkyZJ5thkBAcPmhOzlywxn/v5wcCB0LevOUn7QcrobZleqB0dQ+3oGGpHx0gP7Xin79K30hwLEZGHyPnzMHw4fPopJCSAqyu89BIMGwbqIBMRkfuhxEJE5CFw/TpMnAhjxkBUlFnWrBm89545t0JEROR+KbEQEcnErFaYMwcGD4YTJ8yySpXg/fchmUXKRERE7pkSCxGRTOqnn8zN7H7/3XyePz+MGmVO1NY0JRERcTQlFiIimcz+/TBgACxfbj4PCIC33oJeveAu+zWKiIjcMyUWIiKZRESEOQl72jRzCJSbG7z6KrzzDuTM6ezoREQks1NiISKSwUVHwwcfmBOxo6PNsmeegbFjoVgx58YmIiIPDyUWIiIZVEICzJ5t9kicPm2WPfIITJgAjz/u3NhEROTho8RCRCQDWr3anJi9d6/5vGBBcynZ554Di8W5sYmIyMNJ64KIw1ksFpYkbuebQnXq1KFPnz73fe1OnTrRvHnz+z7P3cyaNYssWbKk+XVEbvXHH9Cwofmzdy9kyWL2UBw4AM8/r6RCREScR4lFBrZ582ZcXV1p1KhRqo8NDQ1l4sSJjg/KyT766CNmzZrl0HMm11bPP/88hw4dcuh1RO7k1Cno0gUqVDB7K9zd4fXX4cgR6NsXPD2dHaGIiDzslFhkYDNmzKBnz5788ssvHD9+3NnhOFVCQgJWq5XAwMAH0pPg7e1Nrly50vw6IlFRMGQIFC0KM2aAYZjDnQ4cMCdsZ8vm7AhFRERMSiwyqOjoaL755hteffVVmjZtmuxf6ZcuXUqVKlXw8vIiR44ctGjRAjCHHR07dozXX38di8WC5f9jJ4YNG0aFChXszjFx4kRCQ0Ntz7dv305YWBg5cuQgMDCQ2rVrs2vXrlTH3qFDB/z8/AgJCWHChAlJ6sTGxjJgwADy5MmDr68vjz76KBs2bLC9njgUadmyZZQqVQpPT0+OHTtmNxTqs88+I0+ePFitVrtzP/XUU3Ts2BGAI0eO8PTTTxMUFISfnx9Vq1Zl7dq1trq3a6ubh0IdPHgQi8XCX3/9ZXedDz74gNDQUAzDAGD//v00adIEPz8/goKCaN++PRcuXEhV28nDIz4ePv/cTChGjoTr16FGDdi8GRYsgMKFnR2hiIiIPSUWt2G9dg3rtWu2L4UARmysWR4bm3zdm77AGnFxZnlMzF3r3osFCxZQvHhxihcvzgsvvMDMmTPtYl2+fDktWrTgySef5Pfff2fdunVUqVIFgO+++468efMyYsQIzpw5w5kzZ1J83aioKDp27MimTZvYunUrRYsWpUmTJkRFRaX4HP3792f9+vUsXryY1atXs2HDBnbu3GlX58UXX+TXX39l/vz5/PHHHzz77LM0adKEI0eO2Opcu3aNMWPG8MUXX7Bv374kPQjPPvssFy5cYP369bayS5cusWrVKtq1awfA1atXadKkCWvXruX333+nYcOGNGvWzNYDlJK2Kl68OJUrV2bOnDl25XPnzqVt27ZYLBbOnDlD7dq1qVChAjt27GDlypWcPXuW5557LsXtJg8HwzA3titfHl5+Gc6ehSJFYNEi+OUXqF7d2RGKiIgkT6tC3cbBSpUBKLr5V9z+P9bg3xkzOD/xI7I824qQkSNtdQ899jjG9esUXrsWj7x5ALg0dy5nx4wloGlTQsa9Z6v7d736JFy6RKEfluJZtOg9xzd9+nReeOEFABo1asTVq1dZt24d9evXB2DUqFG0bt2a4cOH244pX748ANmyZcPV1RV/f3+Cg4NTdd0nnnjC7vlnn31G1qxZ2bhxI02bNr3r8VevXmX69Ol8+eWXhIWFATB79mzy5s1rq3PkyBHmzZvHyZMnyZ07NwD9+vVj5cqVzJkzh4oVKwIQFxfHlClTbPd1q2zZstGoUSPmzp1LvXr1AFi4cCHZsmWzPS9fvrzd8e+++y6LFy9m6dKl9OjRI8Vt1a5dOz755BNG/v9zcejQIXbu3MmXX34JwNSpU6lUqRKjR4+2HTNjxgzy5cvHoUOHKKbNBgT4/XdzpaeffjKfZ89uDoN65RXw8HBubCIiInejHosM6ODBg/z222+0bt0aADc3N55//nlmzJhhq7N7927bl2dHOnfuHK+88grFihUjMDCQwMBArl69muI5HkeOHCE2NpbqN/3ZNVu2bBQvXtz2fNeuXRiGQbFixfDz87P9bNy4kfDwcFs9Dw8PypUrd8frtWvXjkWLFhHz/56jOXPm0Lp1a1xdXQFzWNaAAQMoVaoUWbJkwc/Pj7/++ivVc1Zat27NsWPH2Lp1q+06FSpUoFSpUgDs3LmT9evX291PiRIlbG0iD7cTJ6BDB6hc2UwqPD1hwAD4+2/o1UtJhYiIZAzqsbiN4rvMoTkWb29bWfbOncnWoQO42TdbsV9/Met6ednKsrZtS5Znn4X/f4FNVGTd2iR1U2v69OnEx8eTJ08eW5lhGLi7u3Pp0iWyZs2K901xp5SLi4vdcCowewVu1qlTJ86fP8/EiRMpUKAAnp6eVK9endhbhofdzq3nT47VasXV1ZWdO3faEoDE8puP9/b2ts15uJ1mzZphtVpZvnw5VatWZdOmTXzwwQe21/v378+qVat4//33KVKkCN7e3rRq1SrF95MoJCSEunXrMnfuXKpVq8a8efN4+eWX7WJv1qwZ7733XrLHysMpMtLcHfvDD+HGDbOsXTsYNQoKFHBubCIiIqmlxOI2XHx8kpRZPDywJPOnw2TrurtjcXcHsJs8nFzd1IiPj+fLL79kwoQJNGjQwO61li1bMmfOHHr06EG5cuVYt24dL774YrLn8fDwICEhwa4sZ86cREREYBiG7Qv77t277eps2rSJKVOm0KRJEwBOnDiRqgnIRYoUwd3dna1bt5I/f37AnPdw6NAhateuDUDFihVJSEjg3Llz1KxZ03as1WolMjIyxdcCM/lo0aIFc+bM4e+//6ZYsWJUrlzZ7n46derEM888A5hDtW7uFYHk2yo57dq1Y+DAgbRp04YjR47YepQAKlWqxKJFiwgNDcXNTb92D7u4OHNi9vDhcP68WVa7Nrz/Pvx/KpSIiEiGo6FQGcyyZcu4dOkSXbp0oUyZMnY/rVq1Yvr06QAMHTqUefPmMXToUA4cOMDevXsZN26c7TyhoaH8/PPPnDp1ypYY1KlTh/PnzzNu3DiOHDnC5MmT+fHHH+2uX6RIEb766isOHDjAtm3baNeuXap6R/z8/OjSpQv9+/dn3bp1/Pnnn3Tq1AkXl/8+isWKFaNdu3Z06NCB7777jqNHj7J9+3bGjRvH6tWrU91m7dq1Y/ny5cyYMcM2L+Xm+/nuu+/YvXs3e/bsoW3btklWkUqurZLTokULIiMjefXVV6lbt65dj1L37t25ePEibdq04bfffuOff/5h9erVdO7cOUVJi2QOhgHffw9lykCPHmZSUby4WbZ+vZIKERHJ2JRYZDDTp0+nfv36BAYGJnmtZcuW7N69m127dlGnTh0WLlzI0qVLqVChAk888QTbtm2z1R0xYgTh4eEULlyYnDlzAlCyZEmmTJnC5MmTKV++PL/99hv9+vWzu8aMGTO4dOkSFStWpH379vTq1SvV+zmMHz+eWrVq8dRTT1G/fn0ef/xxu14EgJkzZ9KhQwfeeOMNihcvzlNPPcW2bdvsvqyn1BNPPEG2bNk4ePAgbdu2tXvtww8/JGvWrNSoUYNmzZrRsGFDKlWqZFcnubZKTkBAAM2aNWPPnj22VacS5c6dm19//ZWEhAQaNmxImTJl6N27N4GBgXZJlWRev/1m9ko0bw6HDkHOnDBlirl79lNPacdsERHJ+CxGSga9Z2CRkZEEBgZy5coVAgIC7F67ceMGR48epWDBgnjdx5yHu0kcwhMQEKAvkfdB7egYN7djbGzsA/kdyIzi4uJYsWIFTZo0wf3/wx6TEx4Ob70F8+aZz7284I03zMnZt/yT9NBKaVvKnakdHUPt6BhqR8dID+14p+/St9JgbxGRNHDpEoweDZMmQWys2SPRoQO8+y7ctLqyiIhIpqHEQkTEgWJjYepUGDECLl40y+rVMydm37KxvYiISKaixEJExAEMw9wd+803IXFrktKlYfx4aNRIcyhERCTzU2IhInKftmwx501s2WI+Dw6GkSOhU6ck296IiIhkWvpfHinbtE0kM9Jn//6cOeND69aufPed+dzHB/r3h379wM/PubGJiIg8aA91YpE4u/7atWv3tFO1SEZ37do1AK3YkUr//gsjRrgwZUo94uNdcHGBzp3NDe9y53Z2dCIiIs7xUCcWrq6uZMmShXPnzgHg4+Nj23HakaxWK7Gxsdy4cUPLpN4HtaNjWK1WYmJi+Pfff7lw4QJZsmTB1dXV2WFlCDduwCefmCs7XblitlnDhlbGj3ehbFknByciIuJkD3ViARAcHAxgSy7SgmEYXL9+HW9v7zRJXB4WakfHuLkds2bNavsdkNuzWmHBAnM/ivBws6xsWYOWLbfw1ltVcXdXoisiIvLQJxYWi4WQkBBy5cpFXFxcmlwjLi6On3/+mVq1amnIyX1QOzpGYjvWq1dPm+KlwM8/m3Mmtm83n+fJY/ZYtG4dz6pV550bnIiISDri1MRi6tSpTJ06lfD//wmwdOnSDBkyhMaNGwPmX1aHDx/O559/zqVLl3j00UeZPHkypUuXdngsrq6uaTYcxNXVlfj4eLy8vPSF+D6oHR0jsR01/OnODh40l45dssR87udnPn/9dXOSdhr9HUJERCTDcmr/fd68eRk7diw7duxgx44dPPHEEzz99NPs27cPgHHjxvHBBx/wySefsH37doKDgwkLCyMqKsqZYYtIJnb+PPToYe5BsWQJuLrCK6/A33/D4MFmUiEiIiJJOTWxaNasGU2aNKFYsWIUK1aMUaNG4efnx9atWzEMg4kTJzJ48GBatGhBmTJlmD17NteuXWPu3LnODFtEMqHr12HsWChcGCZPhoQEaNYM9u41d9IOCnJ2hCIiIulbupljkZCQwMKFC4mOjqZ69eocPXqUiIgIGjRoYKvj6elJ7dq12bx5My+//HKy54mJiSEmJsb2PDIyEjDHlafVHIq7Sbyus66fWagdHUPtaM9qhblzLQwd6sqJE+aiAJUqWXnvPSu1a5v7fCTXVGpHx1FbOoba0THUjo6hdnSM9NCOqbm2xXDyDll79+6levXq3LhxAz8/P+bOnUuTJk3YvHkzjz32GKdOnSL3TQvDd+vWjWPHjrFq1apkzzds2DCGDx+epHzu3Ln4aAyDiNzkjz9yMGtWaf75JwsAOXNe44UXDlCz5km0orGIiIi551Xbtm25cuUKAQEBd6zr9B6L4sWLs3v3bi5fvsyiRYvo2LEjGzdutL1+67KihmHccanRQYMG0bdvX9vzyMhI8uXLR4MGDe7aGGklLi6ONWvWEBYWpknH90Ht6BhqR9i/H956y5UVK8zsISDAYOBAKz16uOPtXQ4od9dzqB0dR23pGGpHx1A7Ooba0THSQzsmjv5JCacnFh4eHhQpUgSAKlWqsH37dj766CMGDhwIQEREBCEhIbb6586dI+gOg509PT3x9PRMUu7u7u70D3Z6iCEzUDs6xsPYjhERMGwYTJtmDoFyc4NXX4UhQyzkyOEKpH6lrIexHdOK2tIx1I6OoXZ0DLWjYzizHVNz3XTX2W8YBjExMRQsWJDg4GDWrFljey02NpaNGzdSo0YNJ0YoIhlNdDSMHAlFisBnn5lJRYsWsG8fTJoEOXI4O0IREZGMz6k9Fm+99RaNGzcmX758REVFMX/+fDZs2MDKlSuxWCz06dOH0aNHU7RoUYoWLcro0aPx8fGhbdu2zgxbRDKIhASYPRveeQdOnzbLHnkEJkyAxx93bmwiIiKZjVMTi7Nnz9K+fXvOnDlDYGAg5cqVY+XKlYSFhQEwYMAArl+/zmuvvWbbIG/16tX4+/s7M2wRyQBWrzZ3zN6713xesCCMGQPPPQd3mKYlIiIi98ipicX06dPv+LrFYmHYsGEMGzbswQQkIhneH39A//5mYgGQJYvZY9G9OyQz/UpEREQcxOmTt0VEHOH0aTOBmDkTDAPc3aFnT3O37GzZnB2diIhI5qfEQkQytKgoGD/enDdx7ZpZ9txzMHq0uYu2iIiIPBhKLEQkQ4qPhxkzYMgQOHvWLHvsMXj/fahWzbmxiYiIPIyUWIhIhmIYsGIFDBhgbnQH5jKy770HzzyjidkiIiLOosRCRDKM3383V3r66SfzefbsMHQovPwyeHg4NzYREZGHnRILEUn3TpwwJ2F//bXZY+HpCb17w6BB5qpPIiIi4nxKLEQk3YqMhLFj4cMP4cYNs6xdOxg1CgoUcG5sIiIiYk+JhYikO3Fx8PnnMHw4nD9vltWubU7MrlLFubGJiIhI8pRYiEi6YRiwdKk5MfvQIbOseHFzOdmmTTUxW0REJD1TYiEi6cJvv5kTszdtMp/nzGn2WHTtam52JyIiIumbEgsRcarwcHjrLZg3z3zu5QVvvGH2WgQEODU0ERERSQUlFiLiFJcumbtjT5oEsbHmMKcOHeDddyFvXmdHJyIiIqmlxEJEHqjYWJg6FUaMgIsXzbJ69cyJ2RUqODU0ERERuQ9KLETkgTAMWLQI3nwTjhwxy0qXNidmN2qkidkiIiIZnRILEUlzW7aY8ya2bDGfBwfDyJHQqRO46V8hERGRTEH/SxeRNHPkiNlD8e235nMfH+jf31z9yc/PubGJiIiIYymxEBGH+/dfcxL25MnmZncuLtC5s7l8bO7czo5ORERE0oISCxFxmBs34JNPzKTiyhWzrHFjGDcOypRxbmwiIiKStpRYiMh9s1phwQJzP4rwcLOsfHlzYnZYmFNDExERkQdEiYWI3JeffzbnTGzfbj7PkwdGjYIXXgBXV+fGJiIiIg+OEgsRuSeHDsHAgbBkifncz8+cqP366+YkbREREXm4KLEQkVQ5f96chP3ZZxAfb/ZKdOsGQ4dCUJCzoxMRERFnUWIhIily/Tp89BGMHg1RUWZZs2bw3ntQsqRzYxMRERHnU2IhIndktcKcOTB4MJw4YZZVrgzvvw916jg1NBEREUlHlFiIyG399JM5Mfv3383n+fObPRZt2ph7U4iIiIgkUmIhIkns3w8DBsDy5ebzgACzx6JXL/Dycm5sIiIikj4psRARm4gIGDYMpk0zh0C5ucGrr8KQIZAjh7OjExERkfRMiYWIEB0NH3xgTsSOjjbLWrSAsWOhaFHnxiYiIiIZgxILkYdYQgLMng3vvAOnT5tljz5qTsx+/HHnxiYiIiIZS6oSiytXrrB48WI2bdpEeHg4165dI2fOnFSsWJGGDRtSo0aNtIpTRBxszRoLb74Je/eazwsWNHsonn0WLBbnxiYiIiIZT4rWdTlz5gwvvfQSISEhjBgxgujoaCpUqEC9evXImzcv69evJywsjFKlSrFgwYK0jllE7sPBgzB8eDWefNKNvXsha1aYMAEOHIDnnlNSISIiIvcmRT0W5cuXp0OHDvz222+UKVMm2TrXr19nyZIlfPDBB5w4cYJ+/fo5NFARuX/nz0NYmBsREUG4uxv07Glh8GDIls3ZkYmIiEhGl6LEYt++feTMmfOOdby9vWnTpg1t2rTh/PnzDglORBzHMODFFyEiwkK+fJGsWeNN8eLuzg5LREREMokUDYW6W1Jxv/VFJO19/LG5L4Wnp8Ebb+ygUCFnRyQiIiKZSar3zp09ezbLE3fNAgYMGECWLFmoUaMGx44dc2hwIuIYe/ZA//7m43HjrISGRjk3IBEREcl0Up1YjB49Gm9vbwC2bNnCJ598wrhx48iRIwevv/66wwMUkftz7Rq0aQOxsfDUU/DKK1ZnhyQiIiKZUKr3sThx4gRFihQBYMmSJbRq1Ypu3brx2GOPUadOHUfHJyL3qW9fc8WnkBCYPl2rPomIiEjaSHWPhZ+fH//++y8Aq1evpn79+gB4eXlx/fp1x0YnIvflu+/gs8/MZOKrryBHDmdHJCIiIplVqnsswsLC6Nq1KxUrVuTQoUM8+eSTgLlyVGhoqKPjE5F7dOIEdO1qPh4wAOrVc248IiIikrmlusdi8uTJVK9enfPnz7No0SKyZ88OwM6dO2nTpo3DAxSR1EtIgPbt4dIlqFoVRo50dkQiIiKS2aW4x+Lzzz/nqaeeIjg4mE8++STJ68OHD3doYCJy78aOhY0bwc8P5s0Dd21XISIiImksxT0W8+bNIzQ0lEcffZTRo0ezf//+tIxLRO7Rli0wdKj5eMoUKFzYufGIiIjIwyHFicX69es5c+YMPXv2ZPfu3VSvXp3ChQvTt29fNmzYgNWqJSxFnO3KFWjb1hwK1bYtvPCCsyMSERGRh0Wq5lhkzZqVF154gW+++Ybz588zefJkbty4Qfv27cmZMycdOnTg22+/JTo6Oq3iFZHbMAx49VUID4eCBWHqVC0tKyIiIg9OqidvJ/Lw8KBRo0ZMmTKFEydOsGrVKkJDQxk5ciQffPCBI2MUkRT48ktzPoWrK8ydCwEBzo5IREREHiapXm72dqpUqUKVKlUYMWIEcXFxjjqtiKTA4cPQvbv5eMQIqFbNufGIiIjIwyfViYVhGHz77besX7+ec+fO2c2tsFgsLFq0CHctQSPywMTGmvMpoqOhTh0YONDZEYmIiMjDKNWJRe/evfn888+pW7cuQUFBWDSIW8Sp3nkHduyAbNnM3bVdXZ0dkYiIiDyMUp1YfP3113z33Xc0adIkLeIRkVRYuxbGjTMfT58OefM6Nx4RERF5eKV68nZgYCCFChVKi1hEJBXOnzd31wZ45RVo3typ4YiIiMhDLtWJxbBhwxg+fDjXr19Pi3hEJAUMA158ESIioFQpmDDB2RGJiIjIwy7VQ6GeffZZ5s2bR65cuQgNDU0yUXvXrl0OC05Ekjd5MixfDp6e5hKzPj7OjkhEREQedqlOLDp16sTOnTt54YUXNHlbxAn++AP69TMfjx8P5co5Nx4RERERuIfEYvny5axatYrHH388LeIRkTu4dg3atIGYGGjaFHr0cHZEIiIiIqZUz7HIly8fAdrSV8Qp3ngD9u+HkBCYMQPUYSgiIiLpRaoTiwkTJjBgwADCw8PTIBwRuZ3Fi+HTT81k4ssvIWdOZ0ckIiIi8p9UD4V64YUXuHbtGoULF8bHxyfJ5O2LFy86LDgRMZ08CV27mo/794f69Z0bj4iIiMitUp1YTJw4MQ3CEJHbSUgw96u4eBGqVIGRI50dkYiIiEhSqU4sOnbsmBZxiMhtvPcebNgAvr4wdy54eDg7IhEREZGkUjTHIjo6OlUnTW19EUne1q0wZIj5ePJkKFrUufGIiIiI3E6KEosiRYowevRoTp8+fds6hmGwZs0aGjduzKRJkxwWoMjD6soVaNvWHArVpg106ODsiERERERuL0VDoTZs2MDbb7/N8OHDqVChAlWqVCF37tx4eXlx6dIl9u/fz5YtW3B3d2fQoEF069YtreMWyfS6d4ejRyE0FKZO1dKyIiIikr6lKLEoXrw4Cxcu5OTJkyxcuJCff/6ZzZs3c/36dXLkyEHFihWZNm0aTZo0wcUl1SvYisgtvvoK5swBV1dzXkVgoLMjEhEREbmzVE3ezps3L6+//jqvv/56WsUj8tD7+2947TXz8bBhUL26U8MRERERSRF1L4ikI7Gx5ryKq1ehdm0YNMjZEYmIiIikjBILkXRkyBDYvh2yZjWHQ7m6OjsiERERkZRRYiGSTqxbB+PGmY+/+ALy5XNuPCIiIiKpocRCJB24cMHcXdswoFs3aNHC2RGJiIiIpI4SCxEnMwzo3BnOnIGSJeHDD50dkYiIiEjqpTqxCA0NZcSIERw/fjwt4hF56EyZAj/8AB4eMG8e+Pg4OyIRERGR1Et1YvHGG2/w/fffU6hQIcLCwpg/fz4xMTFpEZtIprd3L7zxhvl4/HgoX9658YiIiIjcq1QnFj179mTnzp3s3LmTUqVK0atXL0JCQujRowe7du1KixhFMqXr16FNG4iJgSefhJ49nR2RiIiIyL275zkW5cuX56OPPuLUqVMMHTqUL774gqpVq1K+fHlmzJiBYRiOjFMk0+nXD/btg+BgmDkTLBZnRyQiIiJy71K18/bN4uLiWLx4MTNnzmTNmjVUq1aNLl26cPr0aQYPHszatWuZO3euI2MVyTS+/96cWwEwezbkzOnceERERETuV6oTi127djFz5kzmzZuHq6sr7du358MPP6REiRK2Og0aNKBWrVoODVQkszh1ylwFCsxeiwYNnBuPiIiIiCOkOrGoWrUqYWFhTJ06lebNm+Pu7p6kTqlSpWjdurVDAhTJTBISzP0qLl6EypVh1ChnRyQiIiLiGKlOLP755x8KFChwxzq+vr7MnDnznoMSyazGj4f168HX11xa1sPD2RGJiIiIOEaqJ2/XrVuXf//9N0n55cuXKVSokEOCEsmMfvsN3nnHfPzJJ1C0qHPjEREREXGkVCcW4eHhJCQkJCmPiYnh1KlTqTrXmDFjqFq1Kv7+/uTKlYvmzZtz8OBBuzqGYTBs2DBy586Nt7c3derUYd++fakNW8SpIiPNpWXj4+H556FjR2dHJCIiIuJYKR4KtXTpUtvjVatWERgYaHuekJDAunXrCA0NTdXFN27cSPfu3alatSrx8fEMHjyYBg0asH//fnx9fQEYN24cH3zwAbNmzaJYsWK8++67hIWFcfDgQfz9/VN1PRFn6d4d/vkHChSATz/V0rIiIiKS+aQ4sWjevDkAFouFjrf8udXd3Z3Q0FAmTJiQqouvXLnS7vnMmTPJlSsXO3fupFatWhiGwcSJExk8eDAtWrQAYPbs2QQFBTF37lxefvnlVF1PxBm+/tr8cXWFuXMhSxZnRyQiIiLieClOLKxWKwAFCxZk+/bt5MiRw+HBXLlyBYBs2bIBcPToUSIiImhw03qcnp6e1K5dm82bNyebWMTExBATE2N7HhkZCZj7bsTFxTk85pRIvK6zrp9ZZMR2PHIEXn3VDbDw9tsJVK1qxdnhZ8R2TI/Ujo6jtnQMtaNjqB0dQ+3oGOmhHVNzbYuRTrbINgyDp59+mkuXLrFp0yYANm/ezGOPPcapU6fInTu3rW63bt04duwYq1atSnKeYcOGMXz48CTlc+fOxcfHJ+1uQOQW8fEWBg2qyeHDWSlV6gIjR/6Kq6uzoxIRERFJuWvXrtG2bVuuXLlCQEDAHeumqMdi0qRJdOvWDS8vLyZNmnTHur169Up5pDfp0aMHf/zxB7/88kuS1yy3DEg3DCNJWaJBgwbRt29f2/PIyEjy5ctHgwYN7toYaSUuLo41a9YQFhaW7L4fkjIZrR3fftuFw4ddyZLFYOnSQPLnb+LskICM147pldrRcdSWjqF2dAy1o2OoHR0jPbRj4uiflEhRYvHhhx/Srl07vLy8+PDDD29bz2Kx3FNi0bNnT5YuXcrPP/9M3rx5beXBwcEAREREEBISYis/d+4cQUFByZ7L09MTT0/PJOXu7u5O/2Cnhxgyg4zQjj/9ZO5ZAfDFFxYKF05/8WaEdswI1I6Oo7Z0DLWjY6gdHUPt6BjObMfUXDdFicXRo0eTfXy/DMOgZ8+eLF68mA0bNlCwYEG71wsWLEhwcDBr1qyhYsWKAMTGxrJx40bee+89h8Uh4kgXLpi7axsGvPQStGzp7IhERERE0l6qd952pO7duzN37ly+//57/P39iYiIACAwMBBvb28sFgt9+vRh9OjRFC1alKJFizJ69Gh8fHxo27atM0MXSZZhQJcucPo0lCgBd+jgExEREclUUr1BXqtWrRg7dmyS8vHjx/Pss8+m6lxTp07lypUr1KlTh5CQENvPggULbHUGDBhAnz59eO2116hSpQqnTp1i9erV2sNC0qVPP4WlS8HDA+bNg/9vxyIiIiKS6aW6x2Ljxo0MHTo0SXmjRo14//33U3WulCxIZbFYGDZsGMOGDUvVuUUetD//hMR1A957DypUcGo4IiIiIg9Uqnssrl69ioeHR5Jyd3f3VM0aF8lMrl+HNm3gxg1o3Bh693Z2RCIiIiIPVqoTizJlytgNVUo0f/58SpUq5ZCgRDKa/v3NHougIJg1C26zGrKIiIhIppXqoVDvvPMOLVu25MiRIzzxxBMArFu3jnnz5rFw4UKHByiS3i1dCpMnm4+//BJy5XJuPCIiIiLOkOrE4qmnnmLJkiWMHj2ab7/9Fm9vb8qVK8fatWupXbt2WsQokm6dPg2dO5uP33gDGjRwbjwiIiIiznJPy80++eSTPPnkk46ORSRDsVqhQwf491+oWBFGjXJ2RCIiIiLOc8/7WOzcuZMDBw5gsVgoVaqUbQM7kYfF+PGwbh34+JhLyyaz4buIiIjIQyPVicW5c+do3bo1GzZsIEuWLBiGwZUrV6hbty7z588nZ86caRGnSLry22/w9tvm448/huLFnRuPiIiIiLOlelWonj17EhkZyb59+7h48SKXLl3izz//JDIykl69eqVFjCLpSlQUtG0L8fHw3HPw4ovOjkhERETE+VLdY7Fy5UrWrl1LyZIlbWWlSpVi8uTJNNDMVXkI9OgBR45A/vzw2WdaWlZEREQE7qHHwmq14u7unqTc3d0dq9XqkKBE0qu5c80lZV1czMdZsjg7IhEREZH0IdWJxRNPPEHv3r05ffq0rezUqVO8/vrr1KtXz6HBiaQn//wDr7xiPh4yBB57zLnxiIiIiKQnqU4sPvnkE6KioggNDaVw4cIUKVKEggULEhUVxccff5wWMYo4XVycOa8iKgoefxwGD3Z2RCIiIiLpS6rnWOTLl49du3axZs0a/vrrLwzDoFSpUtSvXz8t4hNJF4YNg23bzKFPc+aA2z0v1CwiIiKSOd3z16OwsDDCwsIcGYtIurRhA4wZYz6eNs2ctC0iIiIi9lKUWEyaNCnFJ9SSs5KZ/PsvvPACGAZ06QKtWjk7IhEREZH0KUWJxYcffpiik1ksFiUWkmkYBnTtCqdOmRvgffSRsyMSERERSb9SlFgcPXo0reMQSXc++wyWLAEPD5g3D3x9nR2RiIiISPqV6lWhEsXGxnLw4EHi4+MdGY9IurBvH7z+uvl47FioWNG58YiIiIikd6lOLK5du0aXLl3w8fGhdOnSHD9+HDDnVowdO9bhAYo8aDduQJs25n8bNYLevZ0dkYiIiEj6l+rEYtCgQezZs4cNGzbg5eVlK69fvz4LFixwaHAizjBgAOzdC7lywaxZ5i7bIiIiInJnqV5udsmSJSxYsIBq1aphsVhs5aVKleLIkSMODU7kQVu2DBL3eZw9G4KCnBuPiIiISEaR6r/Fnj9/nly5ciUpj46Otks0RDKaM2fgxRfNx6+/bg6DEhEREZGUSXViUbVqVZYvX257nphMTJs2jerVqzsuMpEHyGqFDh3gwgVzonbihngiIiIikjKpHgo1ZswYGjVqxP79+4mPj+ejjz5i3759bNmyhY0bN6ZFjCJpbsIEWLsWfHzMpWU9PZ0dkYiIiEjGkuIei927dwNQo0YNfv31V65du0bhwoVZvXo1QUFBbNmyhcqVK6dVnCJpZscOeOst8/FHH5mb4YmIiIhI6qS4x6JSpUpUrFiRrl270rZtW2bPnp2WcYk8EFFR5tKy8fHQqhV06eLsiEREREQyphT3WPz6669UqlSJN998k5CQENq3b8/69evTMjaRNNezJ/z9N+TPD59/Dlp/QEREROTepDixqF69OtOmTSMiIoKpU6dy4sQJ6tevT+HChRk1ahQnT55MyzhFHG7ePHNJWRcXmDMHsmZ1dkQiIiIiGVeqV4Xy9vamY8eObNiwgUOHDtGmTRs+++wzChYsSJMmTdIiRhGHO3oUXnnFfPzOO/D4486NR0RERCSju689hQsXLsybb77J4MGDCQgIYNWqVY6KSyTNxMdDu3YQGQmPPQZvv+3siEREREQyvlQvN5to48aNzJgxg0WLFuHq6spzzz1HF818lQxg+HDYsgUCA80hUG73/FsgIiIiIolS9ZXqxIkTzJo1i1mzZnH06FFq1KjBxx9/zHPPPYevr29axSjiMBs3wqhR5uPPP4cCBZwbj4iIiEhmkeLEIiwsjPXr15MzZ046dOhA586dKa4F/yUDuXgRXngBDAM6d4bnnnN2RCIiIiKZR4oTC29vbxYtWkTTpk1xdXVNy5hEHM4woGtXOHkSihUzN8ITEREREcdJcWKxdOnStIxDJE1NmwaLF4O7u7nMrJ+fsyMSERERyVzua1UokYxg/37o08d8PGYMVKrk1HBEREREMiUlFpKp3bgBbdrA9evQoAG8/rqzIxIRERHJnJRYSKY2cCD88QfkyvXfLtsiIiIi4nj6miWZ1vLlMGmS+XjWLAgOdmo4IiIiIpmaEgvJlM6cgU6dzMd9+kDjxs6MRkRERCTzU2IhmY7VCh07woULUL48jB3r7IhEREREMj8lFpLpfPABrFkD3t7m0rKens6OSERERCTzU2IhmcrOnfDWW+bjjz6CkiWdG4+IiIjIw0KJhWQaV6+aS8vGxUHLluZO2yIiIiLyYCixkEyjVy84fBjy5TN32rZYnB2RiIiIyMNDiYVkCgsWwMyZ5j4VX38NWbM6OyIRERGRh4sSC8nwwsOhWzfz8eDBUKuWU8MREREReSgpsZAMLT4e2raFyEioUQOGDHF2RCIiIiIPJyUWkqGNGAFbtkBgIMyZA25uzo5IRERE5OGkxEIyrJ9/hlGjzMeffgqhoU4NR0REROShpsRCMqRLl+CFF8xdtjt1gtatnR2RiIiIyMNNiYVkOIYBL70EJ05A0aLw8cfOjkhERERElFhIhjNjhoVFi8DdHebNAz8/Z0ckIiIiIkosJEM5ccKPvn1dARg9GipXdnJAIiIiIgIosZAMJCYGJkyowvXrFsLCoG9fZ0ckIiIiIomUWEiGMXiwC+HhgeTIYTB7trnLtoiIiIikD/pqJhnCjz/CpEnmEKgvvkggJMTJAYmIiIiIHSUWku5FREDHjubjpk2P0KSJ4dyARERERCQJJRaSrlmtZlJx/jyUK2fQocN+Z4ckIiIiIslQYiHp2sSJsHo1eHvDl1/G4+FhdXZIIiIiIpIMJRaSbu3aBW++aT7+8EMoVcq58YiIiIjI7SmxkHTp6lVo0wbi4qBFC+jWzdkRiYiIiMidKLGQdKl3bzh0CPLmhWnTwGJxdkQiIiIicidKLCTd+eYbmDHDTCa+/hqyZXN2RCIiIiJyN0osJF05duy/YU+DB0Pt2s6NR0RERERSRomFpBvx8dCuHVy5AtWqwZAhzo5IRERERFJKiYWkG+++C7/+CgEBMHcuuLs7OyIRERERSSklFpIubNoEI0eajz/9FAoWdG48IiIiIpI6SizE6S5dModAJe6y3aaNsyMSERERkdRSYiFOZRjmZO0TJ6BIEfj4Y2dHJCIiIiL3QomFONWMGfDtt+DmZs6r8Pd3dkQiIiIici+UWIjT/PUX9OplPh41CqpWdW48IiIiInLvlFiIU8TEmHMprl2D+vWhXz9nRyQiIiIi90OJhTjFoEGwezfkyAFffgku+iSKiIiIZGj6OicP3MqV8OGH5uOZMyEkxLnxiIiIiMj9U2IhD9TZs+aSsgA9ekDTps6NR0REREQcQ4mFPDBWK3TqBOfOQdmyMH68syMSEREREUdxamLx888/06xZM3Lnzo3FYmHJkiV2rxuGwbBhw8idOzfe3t7UqVOHffv2OSdYuW8ffWQOg/Lygvnzzf+KiIiISObg1MQiOjqa8uXL88knnyT7+rhx4/jggw/45JNP2L59O8HBwYSFhREVFfWAI5X79fvvMHCg+fjDD6FUKefGIyIiIiKO5ebMizdu3JjGjRsn+5phGEycOJHBgwfTokULAGbPnk1QUBBz587l5ZdffpChyn2IjjaXlo2Lg+bNQW+diIiISOaTbudYHD16lIiICBo0aGAr8/T0pHbt2mzevNmJkUlq9ekDBw9CnjzwxRdgsTg7IhERERFxNKf2WNxJREQEAEFBQXblQUFBHDt27LbHxcTEEBMTY3seGRkJQFxcHHFxcWkQ6d0lXtdZ13emRYssfPGFGxaLwcyZCQQEGNxrMzzM7ehIakfHUDs6jtrSMdSOjqF2dAy1o2Okh3ZMzbXTbWKRyHLLn7cNw0hSdrMxY8YwfPjwJOWrV6/Gx8fH4fGliGGQffVqfj10mGuFC4Grq3PieMDOn/emT586ALRseZhr1w6wYsX9n3fNmjX3fxJROzqI2tFx1JaOoXZ0DLWjY6gdHcOZ7Xjt2rUU1023iUVwcDBg9lyE3LSD2rlz55L0Ytxs0KBB9O3b1/Y8MjKSfPny0aBBAwICAtIu4DuIPnCAMz+tB49fKfTzRlx8fYG7J0kZWXw8hIW5Eh3twiOPWJk9uyDu7gXv65xxcXGsWbOGsLAw3N3dHRTpw0ft6BhqR8dRWzqG2tEx1I6OoXZ0jPTQjomjf1Ii3SYWBQsWJDg4mDVr1lCxYkUAYmNj2bhxI++9995tj/P09MTT0zNJubu7u9PeEHdvby4/8gj58uTBM0sWW/mpvn0x4uLI0b07XiVKOCW2tDJ6NPz6K/j7w7x5Lvj4OG46jzPfy8xE7egYakfHUVs6htrRMdSOjqF2dAynfo9NxXWdmlhcvXqVv//+2/b86NGj7N69m2zZspE/f3769OnD6NGjKVq0KEWLFmX06NH4+PjQtm1bJ0adeh6hoZxr2YIqTZrYyqzR0UStXYcRG0uOnj1t5XHnzgHgnivXA4/TUX79FUaMMB9PnQqFCjk3HhERERFJe05NLHbs2EHdunVtzxOHMHXs2JFZs2YxYMAArl+/zmuvvcalS5d49NFHWb16Nf7+/s4K2WEsPj6Ezp9H9JateBYtaiu/OHs2F6fPIMdrr5KzVy8nRnhvLl+Gtm3NXbbbt4d27ZwdkYiIiIg8CE5NLOrUqYNhGLd93WKxMGzYMIYNG/bggnpALBYLXqVK4XXLTnHxEWcB8CxW/L+yS5e49NXX+DcIS9dDpgzD3KPi+HEoXBgmT3Z2RCIiIiLyoKTbfSweVnkmvE+RjRvwq1PbVnb1p5+4MGUKp996y4mR3d3MmfDNN+DmBvPmmfMrREREROThkG4nbz/M3G9Z9co9Tx786tfDp2IlW5lhtXK0VSu8S5chZ9/Xccua9UGHaefgQUicKvLuu1C1qlPDEREREZEHTIlFBuBbrRq+1arZlV3fs4eY/QeIO36C4HfetpXHHj+OW/bstiVtH4SYGGjTBq5dgyeegP79H9ilRURERCSdUGKRQXmXLk2+L74g/mwEFg8PW/mZwW9z/Y8/yDPhffzr138gsQweDL//Dtmzw1dfgYsG2ImIiIg8dJRYZFAWDw/8Hn/MrswaG0v8+fMYMTF4lihpK7++dy/X9/yBf/16uP9/40FHWbUKJkwwH8+cCblzO/T0IiIiIpJBKLHIRFw8PCj04wpij4bjkTePrfzyokVcnr+AmMOHCRk+zGHXO3cOOnY0H3fvDs2aOezUIiIiIpLBaNBKJmOxWPAsVNCuzLtMGbwrVcK/QZitLO70aY40bcr5SR/fccnf27FaoVMnOHsWypSB8ePvN3IRERERycjUY/EQyNKqFVlatbIri1q7lti/j3At63YsFoutPOaff/AoUACLq+sdz/nxx/Djj+DlZS4t6+2dJqGLiIiISAahxOIhFdi8Oa5Zs+IaEGArM2JjCX++NRY3N0IXzMcjf/5kj929GwYMMB9PmGD2WIiIiIjIw02JxUPKNSCAwFsmRcSEh2NxcQFXV9zz5rWVR65ZA3Fx+NaqzQ2LL23aQGwsPP00vPrqg45cRERERNIjJRZi41WsGEV/2UTsyZNmgvF//079lBv79xPy7kgGrG7FX3+Zqz998QXcNIpKRERERB5imrwtdizu7ngW/G/yt5GQgO9jj+FRuDDro59g2jQzmVjYbw3RfdpzZelSJ0YrIiIiIumFEgu5I4urK7ne6IvHp8vo3CcbAG++CQVOrebajh3c+Ougra5hGMT8c/SeVpkSERERkYxNQ6HkrhIS4IUX4PJleOQRGD4cjLN98C5bBp9q1Wz1Yv/+m3+aPYVniRIUXPTtXVeWEhEREZHMQ4mF3NXo0fDzz+DvD3Pngrs7kDcP2RJ3x/u/G38dxOLujntQkF1ScWn+AjxCC+BTpQoWN33kRERERDIjfcuTO9q82eyhAJgyBQoXvn3dwGZN8atbh4TLl21l1uhozo4ejREbS8Hvv8ereLE0jVdEREREnEOJhdzW5cvQtu1/Q6FeeOHux7j6+eHq52d7nhAdTUCzpsT+fQTPYkVt5ecnTybm4CGydeyAT+XKaRC9iIiIiDxISiwkWYYBr7wCx45BoUIwefK9ncc9Vy5yjxp1y7kNrixdStyx4wQ0bmQrt0ZHY71+HbccOe4ndBERERFxAq0KJcmaPRsWLAA3N3NexU0bdDtEngkfkP3ll/GtWctWFrlyFYdr1uLMO+849mIiIiIikubUYyFJHDoEPXqYj0eMgEcfdez5LRYL3mVK412mtF15zKFDYBi4BQfbygyrlYszZuBbsxYuBUMdG4iIiIiIOIx6LMRObKw5ryI6GurWhQEDHty1gwa9SZH1P5H1+edtZdf37OHc+xM41q4dxMc/uGBEREREJFXUYyF2Bg+GnTshe3b46it40FtRuIeE2D23uLnhV7curtmyYnF3t5WfeqMfLgH+ZO/SFY+8eR5skCIiIiKShBILsVmzBt5/33w8fTrkSQff173LliXf1CkYhkH8/3ssEi5eJPLHH8FqJXuXrra68f/+i4uPDy7e3s4KV0REROShpaFQAsD589Chg/n41Vfh6aedG8+tLBaL7bGLvz/5Pp1Kjh497Horzn/8MYeq1+DSvHnOCFFERETkoaYeizQWE5/As59txS/OheidJ6lYIDtFc/nh5pp+cjrDgBdfhIgIKF0aJkxwdkR3ZnF3x69WLfxq1bIrj/nrIMaNG7jnzWsrizt7lqs//YRfvXq458r1oENNl1x+7E+Vo/tw2foP5HsEQsqDp9/dDxQRERG5AyUWaeyvM1H8cTIScGHzkv0AeLu7UiZPAOXyZqFc3kDK581Cgew+dn+Vf5A+/hiWLwdPT5g3DzLqSKIC8+YSc+AAnkWK2MqiVq3i7Ogx+CxfQYGvv3JidOmHy6EV5Ll6Ftb9ZhZYXCBHcchTyfzJXQmCyoCbh3MDFRERkQxFiUUaC83uy6Tny7Fk026iPbPz56lIomMT2B5+ie3hl2z1svi4UzaPmWSUyxtI+XxZCArwSvP49uyB/v3NxxMmQNmyaX7JNGOxWPAqVcquzC1HDrzLl8e/QZitzIiN5VjHTvhWr072l7o+XHMyDIOEp6ZwaP18SvhH43JmN0SdhvMHzJ/dc8x6rh5mcpGnEuSpbCYbOYqCywOezS8iIiIZhhKLNBbo407jMsEYx600aVIVF1c3/jl/lT0nr/DHycvsOXmFA6cjuXwtjk2HL7Dp8AXbscEBXrYko1zeQMrlyUKgj/sdrpY6165B69bmErPNmsFrrzns1OlGQJMmBDRpgmEYtrLobb9x/fffiT1xghw9utvK486ewy1HdiwPeimsB8liwShYm8MHoinapAku7u4QFQGndsGpnXB6l/n4xmXz8eldsP0L81gPPwipAHkq/pdsZMkPTuppExERkfRFicUD5upioWiQP0WD/GlV2ZwLEBtv5a+ISDPZOHGZP05e4fC5KCIibxCx/war95+1HV8wh6+ZZOTNQoV8gZQKCcTb496+CPftC3/9BSEhMGNG5v5+ePMwM+/y5QgZOwbjRgwWl//mupx89VXizp0j76SP8KlUyRlhOod/MJRoYv6AOenm0tH/Jxv/Ty7O7IHYq3DsF/MnkU92M8HIU/m/YVR+OZ1zHyIiIuJUSizSAQ83l//Pt8gC1QoAEB0Tz5+nrvDHySvsOXmZPScvc+LidY5eiObohWi+330aMBOVYkH+lP9/slE+XyDFgvxxv8vk8O++g88+M5OJr76CHDnS+i7TD9eAALI0b25XlnDlCrEnT2K9ehWP0FBb+fU9e4g7E4Ffzcdx8fV9sIE6i8UC2QqZP2VbmWUJ8XDhoNmrkZhsnN0H1/6Fv9eYP4kC8/2XZOSpZPZyeAU45VZERETkwVFikU75errxaKHsPFoou63sf+3dd3yV5f3/8dd99skZ2YOEDPZegqIijoqIOGutCoq11EHROkvd1doW19dRteLXam37tY7+WkfdggNQW0T2kk12CElIzjlJzr5/f9wnZ5AAQQInCZ/n43E/zjlX7nPOdS5CznmfazU0+1lbofVorCnXhlHVeXxsqnaxqdrF68vLATAbdIzId0Z6NbRhVCWZNnQ67Vv78nK4JrL9w69+BWeeedRfXrejT01l8JdL8W7ahCEjI1re8H+v4HrvPTJmzyb3V/OSWMMk0xsgd4R2HBdZlzjghZp1seFTVSuhbgs0lWvHxncid1a0+Rltw6cKIpPDjUd+DpEQQgghjh4JFj1Ihs3E6UNyOH2ItmyqqqpUN3mjczXWlDeyrqIJty/IyrJGVpY1Ru/rsBgY3TeVUflp/OtPabiCqUw43sJvf9uLxz8dIsVkwjpmTEKZqX8/jIWFOKbE0pdv2zZqfvs7nNOnk37ZpUe7mt2H0QKFx2tHG28TVK2OCxurtJBRt0U71kT2GNEZtZAS37ORPVQmhwshhBA9mASLHkxRFPLTrOSnWZk2sg8A4bDKzvpmLWyUa8OoNlS5cHuDfLWtnq+21cMQ6DsEQlYzP381shJVYRqjC1JJt8kSo/Gy584l6+c/TyhzL1xIy7Jl6CyWhGARqK2VvTIsqdD/NO1o46mN9Wi0TRJvbYDq1drBn7XzjCmRyeHHQf447TK9X++e/COEEEL0IhIsehmdTmFAtp0B2XZ+OE6bHB4Ihdlc4+btJU384f8aMeY1Ysnx0NDqY9GmWhZtqo3evygjhTGFadE5GyMLnKSYju1fk333F3GefwGK2YKpf79oWbi5me1TzsJYWEjxK/+HIT39aFez+7LnwJBp2gHa5PDG0riwsUrr2Qg0Q9nX2tHGmh7r0Wi7dOQl53UIIYQQ4oCO7U+MxwijXkehPZWX7k6lblcRM2fCn34TYmN1E6sjq1CtrWhkV30LZQ3a8e4abXK4ToFBOQ7GFEYmh/dNY0ieA5Oh++wcfrSZ+haQOfunCWXejRtRw2HUQAB9Wlq03P3Z5+jsNlLGj+/dy9geCkWB9BLtGHmxVhYOaUOlomFjBdSsh9a9sP1T7WjjLIj1aORHejesaUl4IUIIIYSIJ8HiGKCq8POfw65d0K8fLFgAKWY9E0oymFASm6jc2OKPhoy2fTZ2u3xs3u1m8243//i2AtBWsRrWx8nYuJWo+mfZo5PDj0Upxx/P4K+/IlBREe3hUFWV3Y88TKC0jIKnnsI57ewk17Ib0+khZ5h2jLtCKwv6YPf62FyNyhWwZzO4KrXju/di988cGOvRKBgPeaPAeAxtfCiEEEJ0AxIsjgF/+xu89hro9fDqq+Dcz8qfaSkmTh2czamDY/sQ1DR5WVPRmLAalcsb1FalKm8ESgGwmw2MKkhldGFs9/CCNGu7YUS9md7pRB+387fq9ZIy7jiaW73YTjklWt70/vt4Pv2U1B/9CPukScmoas9gMEf2xxgfK/O5tT014jf0ayyD+m3ase4f2nk6gxZS4vfYyB6mrW4lhBBCiCNC3mV7ua1b4YbI5tIPPggnnnho989LtZCXmsfZI7Rx7aqqUlrfou2tUa71aqyvasLjC/KfHfX8Z0d99L5ZdlNkf45Y2Mi0m7vqpXV7OquV/IcfQg2HEzbic733Pp7PP8c0YEA0WKjhMKHGxoSlbkUHzA4oOUU72jTXxXo02oZSNe/RlsKtWQcr/6qdZ7BCn9GJYSOjv0wOF0IIIbqIBItezO+HmTOhuRlOPx3uuOPwH1NRFEqybJRk2bhwbAEAwVCYLbs9CUOovqtxU+fx89l3tXz2XWxyeN90azRkjClMY2RBKnZz7/41jA8VAFlzf4554ACc55wTLWtds4bSK67EftppFC547mhXsWezZcGgs7QDtLF/TRWxuRqVK7UlcP1uKF+mHW0sqZH5GnF7bDjzk/IyhBBCiJ6ud3+iO8bddx98+y1kZGi7ax+pucMGvY7h+U6G5zu5/AStzBsIsaHKFRtCVdHIjj3NVOxtpWJvK++vqwa0L4sHZtujczXG9E1jaB8HZkPvnehsHTUK66hRCWWtq9dAOIzOmjgvoPHtt7GOGoV5wICjWcWeTVEgrVA7hl+olYXD2lCp+LBRs07bd2PHF9rRxp4X6dEYF5scniI9SUIIIcTBSLDopRYtgkcf1a6/9BL07Xt0n99i1DO+OJ3xxbFlV5taA6yv1ELG2sgeG9VNXrbWetha6+FfK7XJ4Ua9wrA+TkZHJoePLUxjQLb96L6Aoyzzp1fjOOss1IA/Whbcu5fqu++BcJiBn32KMV++Sf/edDrIHqwdYy7XyoJ+qN0Ym6tRuQr2bAJPDWx+XzvapPeLDZ/KP04bUqXIni9CCCFEPAkWvdCePTBrlnZ9zhy46KKkVicq1Wpk0sAsJg3MipbVur2sjczVWB0ZRtXYEoisTtUElAFgM+kZnu/E7tPBuhqOK8mkb3rvmhxu6luQcDvU2IjtlEmEmpoSQsWeZ54l1NhI+ozLMQ8ceMjP88zqZ9jQsoGG7xoYkD6AIkcRBY4CjDrjYb+GHsVggvyx2sHPtDJ/c2xyeNuGfnt3xo71/9TOU3QYsocxNpSFbmWttvt47gjQH2NtKIQQQsSRYNHLqCr89KdQUwPDh8Pjjye7RgeW47AwZbiFKcNzAW1yeHlDa3QlqjXlTayvaqLZH2L5rr2Ajs//sRaADJuJUQWpCRv6ZTt6z+Rwc79+FL3wAmo4HC1Tw2H2/uMNQnvqsJ9+WjRYhFtaQKdDZ7Ec9HE/Kf2ESn8l36z8JlqmV/Tk2/MpdhZT7CymyFEUvd7H1ge9rvcOTUtgskHxydrRpqUhbiO/yFAqz26U2g0UA3y4WDtPb46bHB7p2cgcqPWWCCGEEMcACRa9zB//CO+/D2aztsRsSkqya3RoFEWhKDOFoswUzh+jfUsfCqtsq/WwsrSe975eR5M+jc273TQ0+1m8ZQ+Lt+yJ3j8/1RKZr6GFjZF9U3Faeva3yAmTv1WVPr/9LZ7Pv8A2cWK0uPGf/6L2qafInD2b7BtvOODjXT/qehatWoQpx0SZp4xydzmtwVbK3eWUu8v5svLLhPONOiN9HX0pdkRChzMWOnJSctApvfyDc0oGDJyiHaCld1cVwbLl7PjynwxMcaGrWg2+JqhYrh1tzM5Ir0hc2EjtKytRCSGE6JUkWPQia9fCL3+pXX/sMRg9Orn16Sp6ncKQPAf9My2k1Kxh+vQTCaHjuxq3NoQqsnv49j0eqpq8VDXV8NGGmuj9+2fbGBtZiWp0YRrD+zixGHvmN/CKXo/j9NNxnH56QnnLypWoLS3o7LZomer30/jOOzjOOANDVmz42Xn9z0P3nY7pk6djNBpRVZXallrK3GXscu2izFVGqauUMlcZZe4yAuEAO5t2srNpZ7v6WPQWCp2F0dARHzwyLZm9aqhalKJAagHq0Bw27VDoN306Or0eGnbEhk9VrdSGVPlcsHOJdrSx5cRCRtulLTN5r0cIIYToIhIseomWFpgxA3w+OO88uPHGZNfoyLIY9Ywt1CZ2X3WSVub2Blhf6UoYRlXZ2MqOPc3s2NPMm6sqATBEgkr8EKpBOXYM+p77zXvBk0/g/dnPMOb3iZY1f7Ocmvt+TV12NgOXLN7vh3xFUci15ZJry+X4vOMTfhYKh6hpqYkGjVJXqXbdXUaluxJvyMvWvVvZundru8e1GW3RIVXxvRzFjmLSLGld+vqTTqeDrIHaMfpSrSwUgNpNiWFj90ZoroUtH2lHm7TiuLAxHvqMAXPvXrBACCFE7yPBope4/XbYuBH69IE///nYHGnhsBg5aUAmJw2Ifftb5/FFQ0bb0rf1zX42VLnYUOXi1ciWBlajnpEFzoQN/YozU3rMN+6KomAdNTKxUA1jGTUKy/DhCa9j9113k9nsIXzqqZCezoHodXoK7AUU2As4Of/khJ8FwgGqPFUdho4qTxXNgWY2NWxiU8Omdo/rNDkTezjihlk5TI7v3xDdid6ozbnoMxrGX62V+Vu0ZW7bwkblCmjYDo2l2rHhLe08RQdZQ7Sw0RY4ckdqE86FEEKIbkqCRS/w1lvw/PPa9b/9DbKzk1uf7iTLbuYHQ3P5wdDY5PDKxtZo0FhT0ci6itjkcG2CuCYtxahNDo+EjbGFaeQ4Dz45uruwT56MffJk1FAoWhaorMT93ntkQsLGJnULFtD4z3+RfsUVZM7+abS8ZeVKjPn5GHJy2m30Z9QZo+FgX/6Qnwp3RWxolVsLH7tcu6htqcXld7Gubh3r6ta1u2+GJSPWuxE3kbzQUUiKsYdNGtqXKQWKJmpHm9a92gZ+0bCxEtxV2tK3ezbB6r9r5+lNWrgoOC62oV/WIDhWJtYLIYTo9iRY9HAVFXDNNdr1efNgypTk1qe7UxSFvukp9E1P4dzR2rChUFhlxx5PdNfwNRVNbKpy0dgSYOnWOpZurYveP89pie4aPrpvKqML0khN6d6Tw5W4AKFLTSXnwQfZ/MknCZvx+XeVEqisRA0EomUhl4vSmVcAMGTVSpTI+e7PPse3ZQu2k0/Cup+JPCa9if5p/emf1r/dz1oCLZS7yylzx/VyRHo86r31NHgbaPA2sKp2Vbv75qTkRMNGibMkOsSq0FGISd9Dv823psOAM7Sjjbsm1qPRFji8jdr1qpWw/EXtPJMd+oxN7NlIKzo2uyyFEEIknQSLHiwU0varaGiACRPgd79Ldo16Jr1OYVCug0G5Di4Zr+0k6A+G+a7GpYWNyOTwrbVualxeajZ6+WTj7uj9+2XZ4jbzS2V4n1Sspu75LbLebsf5w4vYY078EJ7zq3mkXXYphpzcaFlo716Mffui+v0JIcT9ySc0vf02QDRYhFwudl0+A2NBAYULnkMxaH9aArW1KEYj+rS06HCsFGMKQzKGMCRjSLv6efyeaO9GQuhwl9Lka6K2pZballqW1yxPuJ+CQr49nyJHUeJ8Dmcx+fb8nrdHhyMPhk7XDtBWotq7M9aj0TY53O+B0i+1o01KZmyuRlvYsEs3phBCiCNPgkUP9sgj8MUXYLPBq6+CqYd+YdsdmQy6yHyLNDhRG+rT7AuyvlLbuG9NZBhVeUMrO+ua2VnXzDurqwAtqAzOdUQnho8pTGVwrgNjN54cbsjMxJCZuDKRqbiYgYsWJuyjAZASWebWOibWWxGorMS/YwehxsZoqADY8+RTNL31Ftm33UbWddcC2p4be9/4B8a+BTimTEmY/2E32RmROYIRmSPa1bHR25gQOtqGVpW5y2gONFPpqaTSU8l/qv+T+NoUQ+IeHW1zOlKLyUvJ6xl7dCgKZPTXjlGXaGWhINRtTuzZ2L0BWuph20LtaJNamLgSVZ+xYHEm5aUIIYTovSRY9FD//S/8+tfa9T/+EQYNSm59jgU2s4GJ/TOZ2D/2Abyh2R+dFL6mXBtGVefxsanaxaZqF68vLwfAbNAxIt8Z6dXQhlGVZNrQ6br/kJV951ak/fAi0n54UUKZqaiIopf/TLi5OaE87PEAYOwTW63KX1ZG7SOPoE9Px3nWWdHyPX/8I95Nm0ifMQP7pEkAqMEgqs+HzmYjzZJGmiWNMdljEp5DVVXqvfXtJpC3hQ9vyEuZW1s6d2nl0oT7GnVGCh2FFDnjhlY5tPCRm5LbvSfv6w3abt+5I+C4WVpZwAu712tBo61no24LNJVrx8Z3IndWIGtwYtjIHQnGnjOHSAghRPcjwaIHamqCmTO1oVAzZsBVVyW7RseuDJuJ04fkcPqQHED7kFvd5I3O1VhTrk0Od/uCrCxrZGVZY/S+DoshOoRqTKRnI89p6d4fZvdDZ7NhO+mkduV9n3masM+XUKYYDDinn4NiTvwQ2/LNclqWLcM5dWq0zLd9OzsvvAhTSQkDPvowWt7832Wofh+WESMwZGaSZc0iy5rFcbnHJTxmWA1re3REhlOVNpVGez3K3eUEwgF2NO1gR9OOdnW3GqwUOgrb7URe5Cwi09JN950wWqDvBO1o421KnBxetUoLGXWbtWPNa9p5OqMWUuLDRvZQmRwuhBCi0yRY9EA33AA7d0JJCSxYIPM0uxNFUchPs5KfZmXaSO1b+nBYZWd9c3TZ2zUVjWyocuH2BvlqWz1fbauP3j/bYWZMZLnb0YVpjC5IJd3Ws8e46czmhNvmgQMpeOKJdudlzZ2Lb+pZWMeNi5YFqqu1x7DZEs6tW7CAlmXLyH/0EVIvuAAAf2kpe/7wNOYhQ8i6/jrtfoqOXGsOebY8TuhzQsJjhMIhqpur261aVeYqo9JTSWuwlS17t7Bl75Z2dbUb7RQ6CjE0GyhdW0q/tH7R4JFqTv0erXQEWVKh/2na0cZTG+vRaLtsqYfq1drBn7XzjCmxyeH547TL9H7yR0cIIUSHJFj0MP/3f/D3v2srhb76KqR2s88woj2dTmFAtp0B2XZ+OE6bHB4Ihdlc444bQtXI1loPe9w+Fm2qZdGm2uj9izJSEjbzG1ngJMXU+/7r2iaegG1i4od/x+mnM/jb5YRdroRyU78SQo2NmIpjS936tm/H9cEHWEpLo8ECoPyaa/Bt30Gf3/0W++TJAAT37sW3eQu5hX3pW3AyJ7P/PTr2XbmqurkaT8AT3Z9j3frEJXNTzakJ+3LETyS3GRMDUtLYc2DINO0AbXJ4Y2lc2FilBQy/B8q+1o421vTEXcMLjtMmmwshhDjm9b5PJ73Ytm0wd652/YEHoIORJ6KHMOp1jCxIZWRBKjMnFgHQ6g+xoaqJ1ZFVqNZWNLKrvoWyBu14d402OVynwKAcB2MKY8OohuQ5MBm67+Tww6G329HbE3eh7vPAA+3OMw8YQM6vfoXOkXiuv7yC4O7d6FJie2C0rlpNxdy5WIYPp9+b/4qW17/0EmGvl9Tzz6e4qOM9OnwhHxXuCnbs3cHH33xMSkEKFc0VlDaVUttaS5OvibW+taytW9vuvpmWzHaBo20lK6vB2u78o0ZRIL1EO0ZerJWFQ9r8jPiejZp12r4b2z/VjjbOgliPRsF47bpFvvUQQohjjQSLHsLv1+ZVeDxw2mlw113JrpHoalaTngklGUwoyYiWNbb4oyGjbZ+N3S4fm3e72bzbzT++rQC0VayG93EmrETVP8veIyaHdxVTcXHC5n5tSl5/jUBlJeYBA2KF4RCmkhJM/RP32dj7+hsEysuxTZyIqUgLfJ6lS6n57e+wTTqZPvffj1lvZkDaAPJqAvj8Y5h6wmWYIkuyte3R0TaBfFfTruhE8gZvA/Xeeuq99aysXdmunrkpue12Ii92FtPX0Tc5e3To9JAzTDvGafuZEPRFJodH5mpUroQ934GrUju+ey92/8yBsR6NgvGQNwqMSQxPQgghjjgJFj3Er38Ny5dDero2HEov8ymPCWkpJk4dnM2pg2P7ENQ0eVlT0ZiwGpXLG2R1eSOryxuBUgDsZgOjClIZXRjbPbwg7dj7YNfRUrqOKVNwdLCbZPpll+LbtSthiJV/VymBsjJCQxL33aj+xU0MKC/HO3Agpkj3oW5HBVlLl1IwbBhTJ12TcL7b746tXLXPXh0uv4vdLbvZ3bKbb2q+SbifTtHRx9an3STytj06DLqj+GfcYI7sjzE+VuZza3tqRHs2VkBjGdRv0451/4i8EIMWUuL32Mgepq1uJYQQoleQv+g9wKefwqOPatdffBEKC5NbH5FceakW8lLzOHuENq5dVVVK61u0vTXKtV6N9VVNeHxB/rOjnv/siE0Oz7KbGJnvxNCsY89/Ssl2Wsm0mcmwmciym0i3mbr1fhtHWuY117Qrc553LpahQ1AssVCmqiooCqqiYOjbN1resnw5tf/zOPYpZ0aXzAUov34OKAqD7rqTEf21Te9CnmYIBdGnpkb36Nh3Pkepq5SWYEt0j46viZvrgLZHR4GjICF0tC2dm2fLQ6cchX9LswNKTtGONs11sR6Ntj02mvdoQ6lq1sHKv0ZegBX6jEaXN4aBu5tQ1jSBMxdsWZCSpV2ausm8FCGEEAclwaKbq6vTdtdWVbjuOrj44mTXSHQ3iqJQkmWjJMvGhWMLAAiGwmzZ7UkYQvVdjZs6j58vttQBOhZVbu7w8ZwWA1l2LWxk2Exk2k3R8JFpj5TZzGTaTaSnmHrt3I42hvR0DMcfn1CmKArF77/HB+++y8Dc2G7lpuIinOefj3VMbK8NNRTC8/XXEAiQd9+90fKmd95m929/h3P6dAqeeDy6R0fjm2+hTxuB7QcTUVJSqPfWt59E7i6l3FWON+SNlu/LpDO136MjEkByUnKO7LLGtiwYdJZ2gPYHrKki1qNRuVJbAtfvhvJl6MuXMQKg6o32j2VMiYSMzMhldtz1yO22n9uyJYgIIUQSSbDoxlQVZs+G6moYNgyefDLZNRI9hUGvY3i+k+H5Ti6PLLTkDYTYUOViVWk9i1dswpHdh4aWAA3N/ugRVsHlDeLyBtlR13zgJ4lw7BNEsiLhI8NmJnOfMJJh62VBRK9P3Dl88uToylNRqkrhggUEKiowxIWQUL3Wk2TIzoqdGg5Tc//9qIEAAxYtwmSzkWXNwrRkJbkfLOEHp59O2g9vBbQ9OnY3VlDmrU7s5XCXUu4uxx/2s71pO9ubtrerttVgjU4ajx9aVeQoIsOS0fWhQ1EgrVA7hl+olYXD2lCpqpWEqtZQtWU1BekWdK31Wo9Hcx2EfBBogaYy7egMgzXS4xEJGtHr8SEk7ucmmyyfK4QQXUSCRTf23HPw7rtgMsFrr0HcojZCHDKLUc/44nRG59vJ3ruB6dPHYDQaoz8Ph1UaWwM0NPuo9/ipb9aOBo+fhmYfddHrkfJmH2EV3N4gbm+QnYcQRDJtsfARCyKmdj0lGTYTZkPPnlCkGAzYT5nUrjz7ppvIvPZaVL8/Wqa2tmI/4wwC1dUY82IhpHXtGtwff4whNwciu54rKjSdfgHpDgfHvfkvjJFNGn3btuGrrqKxj4Nya0tsInlkj44qTxWtwVY2793M5r3te63sRnvCylVFjliPR5fu0aHTQfZgyB5MePiPWOn/gLzp09G1/U6qqrbcbVvIaIlcNu/R9tyIlu2B5nrtetALwdbYTuOdYbDE9X5kdXw9vsxklyAihBD7IcGim1q3Dm6/Xbv+2GMQN7JCiCNCp1OiH+oH5hz8/HBYpak1oAUQjy8ucGi36+N6Quo8fva2+AmF1WgQ2VXf0ql6OcwGMuKHYNlMZNhNcb0hiT0jPSmI6KxWsMbmbuhsNvo+/Yd25zmnTcOYm4t56NBoWXBPHarPRygYxJARW0ms6e23qX/xJdKvmsWku+9mUsEk1HCY6rvvwdBnGKmzr6Y6vDc2tCqyalWZqyy6R8eG+g1sqN/Qrh5p5rTY0Kq4OR1HZI8ORdHmb5gdkNHv4OerKvib9xM86iJl+1wPerXDVaEdnaE372c4VmZcCIn7udkhQUQIccyQYNENtbbCjBng88H06fCLXyS7RkK0p9MppNu0Cd8Dc+wHPT8cVnF5A9R52gKHLxJKEntB2npL9jb7CYZV3L4gbl+Q0k4GEbvZEDc3pK33wxzXS5LYM2Ixdv8gYh01CuuoUQllhpxsBi/7L4Ga3SiG2J9yXWoq5kEDMcctpRusq6Pp7bdBpyN77lxKjKmUpJZQ++RTuN79nIyrrybjqln4Qj7Kmsqo+fozyuxethobKHWXUeYqo7a1lkZfI417Glm7p/0eHVnWrHarVhU5iyhyFGExWI5Y20QpCpjt2nEoQaSlLtbjEQ0edfv0lLQFkVZteNYhB5GOhmPFzxmJG5olQUQI0YNJsOiGfvlL2LABcnPh5ZflPUb0DjqdQlqKibSUzu3J0BZEYr0gfuqbfTR44npGIkGkrWckGFbx+IJ4fEHKGjoXRGwmPZmRoLFvL0jC5PVIUOkuQURRFPSpqehTE4cnZV17LVnXXpt4rtFI9u23EXa5UeKGv/nLSglUVaGGQwCY9WZKgqkEf/kUWTodM9esjp5f9+F77Nm0ipqReWzLIzq0qsxdRoO3gbrWOupa6zrcoyPPlkexY5+NAZ1FFNoLMeqN7c4/KuKDSHpJ5+7jb95P8IgbjhVfHmiJBJHIPh+doTclTkbfd07IvkOzzE55kxBCdBsSLLqZd97R5lYA/O1vkNOJISlC9EbxQWRA9sHPV1UVV2tQCx+R4Vf76xlpG7oVDKs0+0M0R3Y37wybSU+G3UR6ipGgR8cS33qyHBYtlMQFkLaeke4QRAzp6e3CBkDevfeSMesqjH3yomVhlwtjUREoJIQQ7yefwocfMfrOOzhj6tWA1hNSOusqlL4DaZl/S7R3Y0/Zd5S2VLEpXIE74KGmuYaa5hqW1SxLeP62PToK7YU0Nzez6ptVOC1OHEYHdpMduzFymOw4TA7sRu3SZrQd3f072phs2pHefkf2DiUEkX17Rerj5oxEfh5ohpAf3FXa0Rl6U7Q3RG/N5LhGH7pPvgJHzj4hJDJcy5IqQUQIccRIsOhGKiu1VaBA67WYOjW59RGiJ1EUhdQUI6kpRvp3Noh4g/uZE+JLmB/SEAkrgVBbEGmlvKEV0LFx5YE/AKaY9HG9IQfvGbGajl4Q6WjzQPPAgQz85GNtr4449kmT0FmsWEeOjJYFKirw79yJwedlZPYoRmZrw7Uq/3Ybrg/Wk3PHHehmXEipq5Tyqu8Iv/sJZU4/S/v72eXaRWuwNbpHB8C6bes6XXerwYrD6MBmsiUEkbYAEh9G2m7bTfbouQ6j48j3lhxyEGmJ9XokzAmJG44V/3O/JxJEqsFdjQ4oBFj+n/0/h84YFzg6sYSvJU2CiBCi0yRYdBOhkLZfRUMDjB8Pv/99smskRO+mKAqpViOpViP9sg4+8VhVtfke9ZGgUdvUyuL/riC//xAaW0PtekYamv34Q2Fa/CFa/K1U7G3tVL2sRn37ZXsT5osk7iuSYjoyf8b3XXI27ZJLSLvkkoQy08BBFP3lZcKtia8t3NIKioKxIB+nJZ10SzpDqmDX33/D8Lw8fvHF56iqSl1rHVWPP4Zvy1aWjsrEPGUsLaEWgnvqyF22jQZrmJUjrXgCHjwBD6Y9LgJBH002aKWV1mArdK5ZO2TWm2Ohw5gYPOJDSlsvSUIwifzMrDd33fK8phQwFUFaUefOD7QmDM0Kunbz3YovGVacjb61of1KWn4PhAPRINIpOsMBhmN1MFzLmi5BRIhjmASLbuLRR+Hzz8Fmg1df1ZaYFUJ0H4qi4LQYcVq0IBIIBPDvVJl+Wv+EZXvbtAWRhDkhcT0j+/aS1Hu0INIaCFHZ2EplY+c+MVuMuuiGhR1NTs/ap2ckxaTvsg/CersN24kntisvfH4B4bhldAEUqxXn9OnonA7ttqKQnZKNZ30p3jXfMXbwFZw66nqMRiMtK1dS+sYVGIuKmHfn29HHKLv+epoXL8F5/12Ezz0Dd8BNy9YtmO/4H/w5qXz34Ew8fi2EZH+yGmtFHRvHpLGlUEezvxmfp4mSzU00GH1sLNbhC/nwhXy4PHUEdaDqDr1dDDpD4tCtjnpODvBzh8mB1WD9fv8mRmtsfxBADQTYXuFgyA+mo+/gd5KAdz9zQvZ00CtSr21gGA6Cp0Y7OkNn0AJGZ5fwtaRpSw8LIXoFCRbdwLJlcN992vVnnoHBg5NbHyHE4YsPIiWd7BHx+IJx80AOvnKWPxjGGwh/ryCSuLN6Bz0jkdvfN4jo9vl2xDJkCAVPPN7uvJxbb6V1+3Z2xAURnd2OY9q0hGV0ARSdHsVkwpGWjdOpfZhuKfVRurseqymFK4ZdET23/E9z8Cz+lilnPEj69B8D4N2yhZ2/uxB9ejq5X3yo9YT4Pfh//QiGRf+h7voLqTxnLJ6AB1/tbkY9/QktKTr+/bNheAIe3H43xevrSKtpZlVBgB19IBgO4mppIK20gb0m2JTOIX9jr1f0Wo/IvsFjPz0nHYWWTi33a7RAal/t6IxoENnPcKz4iewt9eBzRYLIbu3oDEUft2JWB3NCEpbwlSAiRHcnwSLJXC6YOVMbCnXZZXD11cmukRAiGRRFwWEx4rAYKc7sXBBp9odiPR+R8FEXWTkrGlDiVtLyfY8gYjbo4vYOiVu2124iqy2gtF23m7AdYhCxnXgipvHjCX7wQbTMMngwfZ96st25hQuei772aP0GD6b4tVfbnes871zMQ4ZgGT48Wqbo9VjHjEHncJBqTo1u+FcesuABRhYcx+ShlwLg27qVHZtfQZ+aynNTnos+RuVXv8K18F1u/NU8LDMuxRPw4KrYSejC2ah6HaXvPoY7MnSrz18WkvvVFtadPYBvJ+fiDrjxeVxM/2cZbkOQF6eoBJQwITVEZmkTuY2NlGcrbMmKtJ+q4miFVhMEDQduUwUFm9GGLqjj5fdfjgaTaG/Jvj0nnZkUf6hBJOjbz6pZ+ynzuUANQXOtdnSGooeUjMTgsd8lfLO0oVkSRIQ4aiRYJNkNN8COHVBcDM8/L0NThRCdoygKdrMBu9nQ6SDS4g/Flu2NLuHbvmekbQK7LxjGFwxT1eSlqsnbqXqZIkGk48np7XtG7OZDfxuKDy56u42UcePanZN6/vntyswDBlDyxuvtygueepKwx4POEttvw5CbS8GTT6CGwwnnphx3HKhgGTQ4+oE9w+qnNCcHDHrO6T89em6VfjNNe1dzXuHZ/OTMnwEQ2L2bbfeeDno9c/62Fm/IiyfgYe/8xwi//R6tV55H7Wln0uxvpsVVz4QrtYD12h8voEnRzh3+2U6Gr2rg61FG3h8bIhAOoKphzlvUhNeo8MHxTfiNWhtlNamkeaDeCXsdB3+DsRqsB5xv0uF8lPi5J/YcjKkFB30eQAsiCatjdbBSVvzQLV9TJIjs0Y7OUHT7H5rV0RK+1vTOPa4QokMSLJLolVe0Q6/X5lWkpSW7RkKI3kpRFGxmAzazgaLMlIOe3xZE4pfo3d/KWW1hxRsI4w+GqW7yUt3ZIKLXkZ5iJBzQs2DH15hNBiwGHWajfp9LHRaDPvHSqMdsiF2a97nd0aVBp7TrUdGZzejM5oQyvdOJ85xz2tU3/fLLSb/88sTXUFTEoCWL252bfdttpM+6CkN2bJkyndVKzrx5qIEAOp2OFF0KKcYU9ANH4J5QTZ8RkziuZBoAgdpatvEk6HT85gcPR+tds/z37C17hfHTr+a3s27R5ok07qbu4bMBlbNvf4ZWs4rH78H51/fI/+fX7DhrGMsuH6kN6fK5uOFX/8FvVPjt3AxqTK14Q14mfhfmpO88rOnXzOdjYh/cT18bpkYP3w5S8Jm0Oli9KpYANFuIhpg2Zr15v0O29jukKzUHe3b/A0+KD/pjq2Xtb6Ws+JW0vE2ghmNBpDNZRNFhsGYwJajDUDEfDBZtLovBDIbIZfxto0U7p+041NsGs3yjKHoVCRZJsn07/Pzn2vX774eTT05ufYQQIl58ECnMOHgQAWjxBxN7QRL2DmnfM9IaCOEPhdnt9gEKe7yeI/uiAJ3CfoNHZ4LJgS7b3T8lDfPADPQGPaqqapsaOp1k/mx2u3plXn01mfuMhTXm5DB0/TrCra0JH7LTL78M24kTtf1G0D7IZ1oyCcycSdnmzZxQPBlTJCjVFdXRmL+LiSOmcu6kOQCEW1vZ7DsOsw/evvRD9HYbgVCA6qeeoHnTXzhp2NlcOXUG7oAbj8/NoEfuRgmrfPr0DOrsYTwBD4M/3MTkt3ewcpyDP1/swOP30BJs4fd/CaJTgzx+sZfS1AYAhpSrDNwaZkcfhbeHxYYljSgNE9Ip7MwlGlgUVUUFDHpjdMhWR/NNoj0nmdk48vp3PCkePUrC6lgHGZrlbQQ1jNJShw1gTyeHZx2uwwkmh3NbAo04AiRYJEEgoM2r8Hhg8mS4++5k10gIIQ5fislASsahB5E6VyufL/2ScRMmElQVfMEQ3kC4w0vffso7vAyE8Aa1XpQ2YZXIEsAhIHCEWqI9nQLmfXtc9rk88M9rYz04Rgvm3BFYwjrM2+qwRO6r/9mNbPxyCUXNAWxhnTZR/9pryLpun53YzWYGLFpEuLkZXYoVAKPeSPaUadiz+2AePARbnxMAUINBKn6gnTt30u3obNqwu7pN/8se3dOcOew8rvjxrwEIhoJsfWwsBEMsOOt5POkWPAEP+tffI2vZ+9ROHsqwkZPx+D24A24uf/ojrM0Bnrq1HztsAZr9zZyw3MU1H4X479Awf7goSKOvEYAb3g1h8cMrZ+jYnaF9IC6oUxm1S6U6HdYMiAWW3L0qIR00OXRYLB0M6TLZsduycRT013pO2oZx6a3Yw2Esvla2fruScyeegkENasv6Bn0QjFx2xW3i9okJerXjaNObj2xwwUCKbze4qsFqj5XLnJdeTYJFEtx/P3zzjTb0qW0olBBCHGvagkiew0iZE04ZmNnh0r2HKxxW8YfC+AJhvJFw0u4yEIpMbj/wpa+T57VdRuugQmsgRGvgSAcaAw+uig3LUhQO3Nvy5d7E3hbHOMx7dFg++i523ozbtcvNe7EYXVr5lB9hPvsSQnpw73ZjMeox6RUyF/wJg6+F1P7Ho4/0mjSfmoInnEP+8OGcNv68aN12DSontHcvz170MsbcXADqfH9mz4ePcUbxDzjtgpujq3Fl/PE29K5mzHNmsSfPitvvJq9yPScvXM22EWl4JxREz7339QZyG+HeWbClrxu338341WGuXhRmY6HCgvNib7qXLA1j86p8PF5HTSSwpLtVxlZaOWPg2TjjllP2bt6M6vdjKilB79CWTQ57vYSamtCZzejjxjO39VB1SFUhFOjaoNLZ22rcnKGQTzto+j6/aAdlBM4C2Dgv8Qd6U9ywsiPdQxM3bE0CzVEhweIo++wzePhh7fqLL0JRJ/dBEkII8f3odAoWnR6LUU8qR3i37TiqqkYnwB9qIPlewSYQptnnJ6gqtC2cpargDWirgR1VixbtE2SOx7xVh+WZL2Pl027TLr+oxmysxWzQkZI5Aftv/4zJbES3wYDFmInZkE34p7dibm2mqM9ZDExPxWLQYxq9HOUH7zBq2HBemnJNpNdHx45XzsPfUsEz5z2Pt1hbjcv/zkfYG/9CysBB/HLCxbj9bjwBDz948Z849jTjOnkY32UoeAIeBm2rY85bburLnk0IFlV33Invu+8ofPFF7KdMAqBl2TLKr5+DZcQI+v3rn9FzS2deQevatfR9+g84zjwTgNbVq6m49TbM/ftT9NKLYNCWZK6ZPx/vho1kzf059kna4/rLyqh98kkM2dnkxQ1raPzXm/h2bMd59g+xjh4NQHDvXlz//jc6my1hE8vWNWsI1NZiGToUU2EhqCphbwu+9WtQdGAZ0DcaPEJ7G1Bb3ehMOnT6UJcEGTXYSsjbjF4NoKih2O9GyK8dvi7+nTsYnbGD+TH7mTtzyLcPEHJ0x9a3xxIsjqK6Om13bVWFa6+FH/0o2TUSQghxpCiKgsWoBRqsRz7QBAIBPvjgA8455xxUnT4hcOw7nGz/PTYHHmJ2oKFo3mCIuJWAo6Hq+4vfCyNNO97YmHiKcxpUAg9+Ei0yjbsRy/E6zO81YzHuwmzQkxEcRf6ld6FYrTQtL4kOH9s0UcHe3ER6+jmcaMnF4tCR1WcltX3/wqAhQxKeypCdTcjVhC4lNtRPDYfBYEDZp6dNDQa1deTjviUPt7QQrK6O9na08X23mdYVKwg3xXoOgvX1uD/8CGNhYcJ4affChXi++AJz//6xYFFby+6HHkafmZkQLBr++ldcH3xI7t13k3HVLFAUgnvq2TXrZygpKQxduSLW0s/eQ9O/3iT71lvJuv467XHr6tg6+VQUk4khq1dFe2D2PP0MTe+8Q/qVV5L506u119baStnsn6EYDBS++Cd0ZjPBQIClv5/PIJcL52mnkjrtB1rg8LdQ+/TzKIpK1oxz0RlUCPpo3biZ1s07MRekYRuUGx0i5v52G6gBbAOc6JQABLwE97oJNHowmEIYU4LRYBN0eSHkRa/zoYRbtX1Vov8AAfAFkhNoDtq7sv/gotOZKNmzDZpPgLQ+R7nyh65HBIvnnnuOxx57jOrqakaMGMFTTz3F5MmTk12tQ6KqcN11eqqqYOhQeLL9Eu1CCCHEYVMUBZNBj9mgx2k5uj00gZDadXNkOtlj4w2ECMcFGn/bvBpvcJ8aZoIfaIpNyn7LMBJSgTUuwBUptZExaS7L7jo74d5Ff3qh3Wt2nHEGw9avS9hbBaDoxT8R9vrQpzqjZZbRoyn5f/8PxZT4b5J9800E99RhHTM6WmYsKCD3nnsSQgyA46yzMPXrhzluJ12dzY7z3HOj81/amEpKsI4bhyEyzAwARcFYUIASt7QyQFsDKobYx0I1EABVRQ2HE4Z1BRvqCVRWEvbEFltQ/X5aV63SHiMuTJmrqvAsWYIpL4/UCy8EswOMfhpeewuAzJvvhFRtPxnPR99R9+f3SZtxObYrYvOCKm4YDYEAA7/4HF1eHgBNL71E7Uv/Q+qFF5L/yMPRc7efMJGwK0z/DxZh7t8PQkH2vvp3ah75H5xnnkrBr2+L9qjsvPE+Qk1uCu+6GnOfVAh68azYRP2//4u1fxY5F4zSwk3Ay+631xFyt5I5OQdzKhD04q1241rvwugMkz44HO2xadoaJuwLYy/wYkwJQzhAsClEa30AvbmJlOzYZqA+lwE1BEZbCL1J+zdQQxAK6FD0Knqjih4YAwQ8syVYdIU33niDW265heeee45Jkybxv//7v5xzzjls3LiRoh40juijj0p47z0dJhO89hrYOrFJqhBCCNFTaIFGwWTQ4bAc/PyuFAh1EEQ66Jlp12PTQVBp9Qdp2lN1SM+/73wKfWoq+tTEc/R2O9ZRI9vdN2X8+HZlxpwcMmZd2a487UcXtysz9S2g4PH/aVeefdNNZN90U+K5hYUM/HRRu3PzH5pP/kPzEwKSISeHQUuXoIZCCedmXXstaRddlBBYFKuVgqf/oPXSxIUTz/DhDD5xIrZRo2IPoChkzJ6NGgwkBBzzoIE4zpmGdcSIhOezjh6NGgigxC0JrVitGPLy0Kfvs+9IZN8ZxRipg96AqioQDILeApkDoqcG9rgI1dejFk+GIVpQC2z7f7RseRNdwRD4wb3Rc91PnkWgYg/pdz4NY8cC4Hv/fer/+ktSJk4k/da/RM+tP/8CfFu3UnT9cxgnjIFAK61fLKbijt9iGTqAfvPuivbGVM17Cu/WCvreehGO0X0h6KVl/S7K/rAIc56D/rdNJOxvoaailGxrRrt/t+6o2weLJ554gp/97Gdcc801ADz11FN8/PHHLFiwgIceeijJteuc9evh5Ze1PyaPPBL9nRRCCCFEFzDqdRj1uu+14eK+tCFlFV1Qq54nPiApen3CHixtjAUFGAsSN0HUmUw4p05td663Xwlp06cnLMqgGI3k/mpeu3Od06bhnDatXXnJ319pV5YxcyYZM2e2Kx/y7XJteFrc60i75BIcU6eimEwJ5xa+8L+oPh+mwtjO8raTTqLgqScxZGUlnJv18zmEGpsw5OdHy0wlJWT85CcYixO/5LZNmoSppARDn77aLvGAPn8Q1jFjMA0aCCWTouca8t/F0OhDN/oCOOkkAFTlK2ARpPeFC54hFAiw/IMPmO7Mpyfo1sHC7/ezYsUK7rzzzoTyqVOn8vXXX3d4H5/Ph88XG0Dncmldm4FAgEDg6C0t2Ka1Fa68Uo/fr2Pq1BBz54ZJQjV6hbZ/v2T8O/Ym0o5dQ9qx60hbdg1px64h7dg1uk07Go2QmYm6T10MkeFkISAUKVdyc7FGemLiz7VdcEH0elu5YfBgMn55e7tzM26/rd25xrFjKXjl/9qdm/fsM+3ONU88gQFr10AolPDZNZnteCjPraj7DgzsRqqqqigoKOCrr77i5Lgd5ObPn89f//pXNm/e3O4+DzzwAL/5zW/alb/66qukpHRubfWu9M03eTz00Amkpvp46qnPSUvzH/xOQgghhBBCdAMtLS3MnDmTpqYmnE7nAc/t1j0WbfYdu3ig9aHvuusubrstlhZdLheFhYVMnTr1oI1xJEyfDief7GPFihX8+MenHZE12o8VgUCAhQsXctZZZ0k7HgZpx64h7dh1pC27hrRj15B27BrSjl2jO7Rj2+ifzujWwSIrKwu9Xk9NTU1CeW1tLbnxqxzEMZvNmOMm+LQxGo1J+weZOhWCwbqk1qE3kXbsGtKOXUPasetIW3YNaceuIe3YNaQdu0Yy2/FQnrdbb0NoMpkYP348CxcuTChfuHBhwtAoIYQQQgghRHJ16x4LgNtuu41Zs2YxYcIETjrpJF544QXKysqYM2dOsqsmhBBCCCGEiOj2weKyyy6jvr6eBx98kOrqakaOHMkHH3xAcXFxsqsmhBBCCCGEiOj2wQJg7ty5zJ07N9nVEEIIIYQQQuxHt55jIYQQQgghhOgZJFgIIYQQQgghDpsECyGEEEIIIcRhk2AhhBBCCCGEOGwSLIQQQgghhBCHTYKFEEIIIYQQ4rBJsBBCCCGEEEIcNgkWQgghhBBCiMMmwUIIIYQQQghx2CRYCCGEEEIIIQ6bBAshhBBCCCHEYTMkuwJHmqqqALhcrqTVIRAI0NLSgsvlwmg0Jq0ePZ20Y9eQduwa0o5dR9qya0g7dg1px64h7dg1ukM7tn2GbvtMfSC9Pli43W4ACgsLk1wTIYQQQggheia3201qauoBz1HUzsSPHiwcDlNVVYXD4UBRlKTUweVyUVhYSHl5OU6nMyl16A2kHbuGtGPXkHbsOtKWXUPasWtIO3YNaceu0R3aUVVV3G43+fn56HQHnkXR63ssdDodffv2TXY1AHA6nfKfqwtIO3YNaceuIe3YdaQtu4a0Y9eQduwa0o5dI9nteLCeijYyeVsIIYQQQghx2CRYCCGEEEIIIQ6bBIujwGw2c//992M2m5NdlR5N2rFrSDt2DWnHriNt2TWkHbuGtGPXkHbsGj2tHXv95G0hhBBCCCHEkSc9FkIIIYQQQojDJsFCCCGEEEIIcdgkWAghhBBCCCEOmwSLI+y5556jX79+WCwWxo8fz9KlS5NdpR7noYce4vjjj8fhcJCTk8NFF13E5s2bk12tHu2hhx5CURRuueWWZFelR6qsrOTKK68kMzOTlJQUxo4dy4oVK5JdrR4lGAxy77330q9fP6xWK/379+fBBx8kHA4nu2rd2pIlSzj//PPJz89HURTefvvthJ+rqsoDDzxAfn4+VquV008/nQ0bNiSnst3cgdoyEAhwxx13MGrUKGw2G/n5+Vx11VVUVVUlr8Ld1MF+J+Ndf/31KIrCU089ddTq11N0ph03bdrEBRdcQGpqKg6HgxNPPJGysrKjX9kDkGBxBL3xxhvccsst3HPPPaxatYrJkydzzjnndLtfgu5u8eLF3HDDDfz3v/9l4cKFBINBpk6dSnNzc7Kr1iMtX76cF154gdGjRye7Kj3S3r17mTRpEkajkQ8//JCNGzfy+OOPk5aWluyq9SiPPPIIzz//PM8++yybNm3i0Ucf5bHHHuOZZ55JdtW6tebmZsaMGcOzzz7b4c8fffRRnnjiCZ599lmWL19OXl4eZ511Fm63+yjXtPs7UFu2tLSwcuVK7rvvPlauXMmbb77Jli1buOCCC5JQ0+7tYL+Tbd5++22WLVtGfn7+UapZz3Kwdty+fTunnHIKQ4cO5YsvvmDNmjXcd999WCyWo1zTg1DFEXPCCSeoc+bMSSgbOnSoeueddyapRr1DbW2tCqiLFy9OdlV6HLfbrQ4aNEhduHChetppp6k333xzsqvU49xxxx3qKaeckuxq9HjnnnuuOnv27ISyiy++WL3yyiuTVKOeB1Dfeuut6O1wOKzm5eWpDz/8cLTM6/Wqqamp6vPPP5+EGvYc+7ZlR7755hsVUEtLS49OpXqg/bVjRUWFWlBQoK5fv14tLi5Wn3zyyaNet56ko3a87LLLesTfR+mxOEL8fj8rVqxg6tSpCeVTp07l66+/TlKteoempiYAMjIyklyTnueGG27g3HPPZcqUKcmuSo/173//mwkTJvDjH/+YnJwcxo0bx5/+9KdkV6vHOeWUU/j000/ZsmULAGvWrOHLL79k+vTpSa5Zz7Vz505qamoS3nfMZjOnnXaavO90gaamJhRFkd7JQxQOh5k1axbz5s1jxIgRya5OjxQOh3n//fcZPHgwZ599Njk5OUycOPGAw86SRYLFEVJXV0coFCI3NzehPDc3l5qamiTVqudTVZXbbruNU045hZEjRya7Oj3K66+/zsqVK3nooYeSXZUebceOHSxYsIBBgwbx8ccfM2fOHG666Sb+9re/JbtqPcodd9zBjBkzGDp0KEajkXHjxnHLLbcwY8aMZFetx2p7b5H3na7n9Xq58847mTlzJk6nM9nV6VEeeeQRDAYDN910U7Kr0mPV1tbi8Xh4+OGHmTZtGp988gk//OEPufjii1m8eHGyq5fAkOwK9HaKoiTcVlW1XZnovBtvvJG1a9fy5ZdfJrsqPUp5eTk333wzn3zySfcbj9nDhMNhJkyYwPz58wEYN24cGzZsYMGCBVx11VVJrl3P8cYbb/DKK6/w6quvMmLECFavXs0tt9xCfn4+P/nJT5JdvR5N3ne6ViAQ4PLLLyccDvPcc88luzo9yooVK/jDH/7AypUr5XfwMLQtanHhhRdy6623AjB27Fi+/vprnn/+eU477bRkVi+B9FgcIVlZWej1+nbfEtXW1rb7Nkl0zi9+8Qv+/e9/8/nnn9O3b99kV6dHWbFiBbW1tYwfPx6DwYDBYGDx4sU8/fTTGAwGQqFQsqvYY/Tp04fhw4cnlA0bNkwWZThE8+bN48477+Tyyy9n1KhRzJo1i1tvvVV61A5DXl4egLzvdKFAIMCll17Kzp07WbhwofRWHKKlS5dSW1tLUVFR9L2ntLSU22+/nZKSkmRXr8fIysrCYDD0iPceCRZHiMlkYvz48SxcuDChfOHChZx88slJqlXPpKoqN954I2+++SafffYZ/fr1S3aVepwzzzyTdevWsXr16ugxYcIErrjiClavXo1er092FXuMSZMmtVvueMuWLRQXFyepRj1TS0sLOl3iW5Ber5flZg9Dv379yMvLS3jf8fv9LF68WN53voe2ULF161YWLVpEZmZmsqvU48yaNYu1a9cmvPfk5+czb948Pv7442RXr8cwmUwcf/zxPeK9R4ZCHUG33XYbs2bNYsKECZx00km88MILlJWVMWfOnGRXrUe54YYbePXVV3nnnXdwOBzRb+NSU1OxWq1Jrl3P4HA42s1JsdlsZGZmylyVQ3Trrbdy8sknM3/+fC699FK++eYbXnjhBV544YVkV61HOf/88/n9739PUVERI0aMYNWqVTzxxBPMnj072VXr1jweD9u2bYve3rlzJ6tXryYjI4OioiJuueUW5s+fz6BBgxg0aBDz588nJSWFmTNnJrHW3dOB2jI/P59LLrmElStX8t577xEKhaLvPRkZGZhMpmRVu9s52O/kvoHMaDSSl5fHkCFDjnZVu7WDteO8efO47LLLOPXUUznjjDP46KOPePfdd/niiy+SV+mOJHdRqt7vj3/8o1pcXKyaTCb1uOOOkyVSvwegw+Pll19OdtV6NFlu9vt799131ZEjR6pms1kdOnSo+sILLyS7Sj2Oy+VSb775ZrWoqEi1WCxq//791XvuuUf1+XzJrlq39vnnn3f49/AnP/mJqqrakrP333+/mpeXp5rNZvXUU09V161bl9xKd1MHasudO3fu973n888/T3bVu5WD/U7uS5ab7Vhn2vGll15SBw4cqFosFnXMmDHq22+/nbwK74eiqqp65OOLEEIIIYQQojeTORZCCCGEEEKIwybBQgghhBBCCHHYJFgIIYQQQgghDpsECyGEEEIIIcRhk2AhhBBCCCGEOGwSLIQQQgghhBCHTYKFEEIIIYQQ4rBJsBBCCCGEEEIcNgkWQgghhBBCiMMmwUIIIcQhe+CBBxg7dmzSnv++++7juuuu69S5v/zlL7npppuOcI2EEEIoqqqqya6EEEKI7kNRlAP+/Cc/+QnPPvssPp+PzMzMo1SrmN27dzNo0CDWrl1LSUnJQc+vra1lwIABrF27ln79+h35CgohxDFKgoUQQogENTU10etvvPEGv/71r9m8eXO0zGq1kpqamoyqATB//nwWL17Mxx9/3On7/OhHP2LgwIE88sgjR7BmQghxbJOhUEIIIRLk5eVFj9TUVBRFaVe271Coq6++mosuuoj58+eTm5tLWloav/nNbwgGg8ybN4+MjAz69u3Ln//854Tnqqys5LLLLiM9PZ3MzEwuvPBCdu3adcD6vf7661xwwQUJZf/85z8ZNWoUVquVzMxMpkyZQnNzc/TnF1xwAa+99tpht40QQoj9k2AhhBCiS3z22WdUVVWxZMkSnnjiCR544AHOO+880tPTWbZsGXPmzGHOnDmUl5cD0NLSwhlnnIHdbmfJkiV8+eWX2O12pk2bht/v7/A59u7dy/r165kwYUK0rLq6mhkzZjB79mw2bdrEF198wcUXX0x8h/wJJ5xAeXk5paWlR7YRhBDiGCbBQgghRJfIyMjg6aefZsiQIcyePZshQ4bQ0tLC3XffzaBBg7jrrrswmUx89dVXgNbzoNPpePHFFxk1ahTDhg3j5ZdfpqysjC+++KLD5ygtLUVVVfLz86Nl1dXVBINBLr74YkpKShg1ahRz587FbrdHzykoKAA4aG+IEEKI78+Q7AoIIYToHUaMGIFOF/u+Kjc3l5EjR0Zv6/V6MjMzqa2tBWDFihVs27YNh8OR8Dher5ft27d3+Bytra0AWCyWaNmYMWM488wzGTVqFGeffTZTp07lkksuIT09PXqO1WoFtF4SIYQQR4YECyGEEF3CaDQm3FYUpcOycDgMQDgcZvz48fz9739v91jZ2dkdPkdWVhagDYlqO0ev17Nw4UK+/vprPvnkE5555hnuueceli1bFl0FqqGh4YCPK4QQ4vDJUCghhBBJcdxxx7F161ZycnIYOHBgwrG/VacGDBiA0+lk48aNCeWKojBp0iR+85vfsGrVKkwmE2+99Vb05+vXr8doNDJixIgj+pqEEOJYJsFCCCFEUlxxxRVkZWVx4YUXsnTpUnbu3MnixYu5+eabqaio6PA+Op2OKVOm8OWXX0bLli1bxvz58/n2228pKyvjzTffZM+ePQwbNix6ztKlS5k8eXJ0SJQQQoiuJ8FCCCFEUqSkpLBkyRKKioq4+OKLGTZsGLNnz6a1tRWn07nf+1133XW8/vrr0SFVTqeTJUuWMH36dAYPHsy9997L448/zjnnnBO9z2uvvca11157xF+TEEIcy2SDPCGEED2KqqqceOKJ3HLLLcyYMeOg57///vvMmzePtWvXYjDI1EIhhDhSpMdCCCFEj6IoCi+88ALBYLBT5zc3N/Pyyy9LqBBCiCNMeiyEEEIIIYQQh016LIQQQgghhBCHTYKFEEIIIYQQ4rBJsBBCCCGEEEIcNgkWQgghhBBCiMMmwUIIIYQQQghx2CRYCCGEEEIIIQ6bBAshhBBCCCHEYZNgIYQQQgghhDhsEiyEEEIIIYQQh+3/A5OeFbeYL5voAAAAAElFTkSuQmCC", + "text/plain": [ + "<Figure size 800x500 with 1 Axes>" + ] + }, + "metadata": {}, + "output_type": "display_data" + } + ], + "source": [ + "dvdt = (v[1:] - v[:-1]) / (t[1:] - t[:-1])\n", + "dvdt_cd = (v[2:] - v[:-2]) / (t[2:] - t[:-2])\n", + "\n", + "# Analytical derivative of v(t)\n", + "dvdt_actual = 9.81 * np.exp(-9.81 * t / 42.78)\n", + "\n", + "# Plotting\n", + "plt.figure(figsize=(8, 5))\n", + "plt.plot(t, v, label='Velocity (m/s)', color='blue')\n", + "plt.plot(t[:-1], dvdt, label='Forward difference')\n", + "plt.plot(t[1:], dvdt, label='Backward difference')\n", + "plt.plot(t[1:-1], dvdt_cd, label='Central difference')\n", + "plt.plot(t, dvdt_actual, label='Actual derivative', linestyle='dotted')\n", + "#plt.axhline(y=42.78, color='red', linestyle='--', label=f'Terminal velocity')\n", + "plt.title('Falling Object Approaching Terminal Velocity')\n", + "plt.xlabel('Time (s)')\n", + "plt.ylabel('Velocity (m/s)')\n", + "plt.grid(True)\n", + "plt.legend()\n", + "plt.tight_layout()\n", + "plt.show()" + ] + }, + { + "cell_type": "markdown", + "id": "2a9c23e9-ec7a-4a8a-a189-f9d58a6d3f52", + "metadata": {}, + "source": [ + "## Comparing Forward, Backward and Central Difference" + ] + }, + { + "cell_type": "code", + "execution_count": 6, + "id": "ea8d487e-96db-4347-a561-71ee4d9b1257", + "metadata": {}, + "outputs": [ + { + "data": { + "image/png": "iVBORw0KGgoAAAANSUhEUgAAAxYAAAHqCAYAAACZcdjsAAAAOnRFWHRTb2Z0d2FyZQBNYXRwbG90bGliIHZlcnNpb24zLjEwLjAsIGh0dHBzOi8vbWF0cGxvdGxpYi5vcmcvlHJYcgAAAAlwSFlzAAAPYQAAD2EBqD+naQABAABJREFUeJzs3XdYFEcfwPHvHr03pagIVqyIXTQCtqCosffejRpjiyb23mJLTCzxtZfYW6yx94IFG4gVRQVRUen19v1jw+kJKAqCZT7Pc493s7Ozs3N3uL/bKZIsyzKCIAiCIAiCIAiZoMrpCgiCIAiCIAiC8PkTgYUgCIIgCIIgCJkmAgtBEARBEARBEDJNBBaCIAiCIAiCIGSaCCwEQRAEQRAEQcg0EVgIgiAIgiAIgpBpIrAQBEEQBEEQBCHTRGAhCIIgCIIgCEKmicBCEARBEARBEIRME4GFIAg0adIEIyMjXrx4kW6edu3aoaenx+PHjzNcriRJjB07NvMVzGD5/v7+jB07lqCgoI92zHdZt24dJUuWxMjICEmS8PPzy7G6ZLexY8ciSdIH7bts2TIkScrR9+5NnTt3xtnZOaer8d68vLzw8vLK6Wp8dHPnzqVw4cLo6+sjSRIvXrzI1Hv2Pp/Br6WNBeF9icBCEAS6detGXFwca9asSXP7y5cv2bJlCw0aNMDOzi6ba5e+U6dO0b17d81rf39/xo0bl2MXp0+ePKFDhw4UKlSIPXv2cOrUKYoWLZojdREyb9SoUWzZsiWnq/He5s2bx7x583K6Gh+Vn58f/fv3p0aNGhw8eJBTp05hZmaWqTLr16/PqVOncHBwyKJaCsLXRzenKyAIQs6rV68eefLkYcmSJfTp0yfV9r///pvY2Fi6deuWA7VLX5UqVXK6Clpu3LhBYmIi7du3x9PTM6erI2RSoUKFcroKH6REiRI5XYWP7tq1awD06NGDSpUqZUmZuXPnJnfu3FlSliB8rcQdC0EQ0NHRoVOnTpw/f54rV66k2r506VIcHByoV68eAKGhofTq1Yt8+fKhr69PgQIFGDduHElJSe881tWrV2nUqBFWVlYYGhri5ubG8uXLU+V78eIFgwcPpmDBghgYGGBra4uPjw/Xr1/X5Hm9K9SyZcto0aIFADVq1ECSJCRJYtmyZUyYMAFdXV2Cg4NTHadr167Y2NgQFxf31npv374dd3d3jI2NMTMzo06dOpw6dUqzvXPnznzzzTcAtGrVCkmS3tpV4smTJ/Tp04cSJUpgamqKra0tNWvW5NixY2+tRwpnZ2caNGjAli1bcHV1xdDQkIIFC/L777+nyhsREcGQIUMoUKAA+vr65M2blwEDBhAdHa2VT5Ik+vXrx8qVKylevDjGxsaUKVOGHTt2pCpz586duLm5YWBgQIECBZgxY0aqPEFBQZr34E0Z6Sbn7OxM586dU6W/2Q3l8OHDSJLEmjVrGDZsGA4ODpiamtKwYUMeP35MZGQkPXv2JFeuXOTKlYsuXboQFRX11mND2l2h3qeN3hQXF8fgwYNxc3PDwsICa2tr3N3d2bZt2zv3HTBgACYmJkRERKTa1qpVK+zs7EhMTATS7qYzf/58ypQpg6mpKWZmZhQrVozhw4dr5Xn48CE9e/bE0dERfX198uTJQ/PmzbW6P96/f5/27dtja2uLgYEBxYsXZ+bMmajVak2elPfj8OHDWuWn9Xm4c+cOrVu3Jk+ePBgYGGBnZ0etWrXe2oXQy8uL9u3bA1C5cmUkSUrzc5LeMVO8+RlMqyuULMtMnz4dJycnDA0NKVeuHLt37063boLwtRN3LARBAJQL7KlTp7JkyRJmz56tSff39+fs2bP8/PPP6OjoEBoaSqVKlVCpVIwePZpChQpx6tQpJk6cSFBQEEuXLk33GIGBgVStWhVbW1t+//13bGxsWLVqFZ07d+bx48cMHToUgMjISL755huCgoIYNmwYlStXJioqiqNHjxISEkKxYsVSlV2/fn0mT57M8OHD+fPPPylXrhyg/OosyzKTJk1i4cKFTJw4UbNPeHg4a9eupV+/fhgaGqZb7zVr1tCuXTu+/fZb/v77b+Lj45k+fTpeXl4cOHCAb775hlGjRlGpUiX69u3L5MmTqVGjBubm5umWGR4eDsCYMWOwt7cnKiqKLVu2aMrMSP9tPz8/BgwYwNixY7G3t2f16tX8+OOPJCQkMGTIEABiYmLw9PTkwYMHDB8+HFdXV65du8bo0aO5cuUK+/fv1xoXsXPnTnx9fRk/fjympqZMnz6dJk2aEBgYSMGCBQE4cOAAjRo1wt3dnbVr15KcnMz06dPfa/zNxzB8+HBq1KjBsmXLCAoKYsiQIbRp0wZdXV3KlCnD33//zcWLFxk+fDhmZmZpBmEZkZE2Skt8fDzh4eEMGTKEvHnzkpCQwP79+2natClLly6lY8eO6e7btWtXfvvtN9avX6/V/e/Fixds27aNvn37oqenl+a+a9eupU+fPvzwww/MmDEDlUrFrVu38Pf31+R5+PAhFStWJDExUfM5efbsGXv37uX58+fY2dnx5MkTqlatSkJCAhMmTMDZ2ZkdO3YwZMgQbt++/UHdr3x8fDSfn/z58/P06VNOnjz51vFe8+bN4++//2bixIksXbqUYsWKfbQ7DePGjWPcuHF069aN5s2bExwcTI8ePUhOTsbFxeWjHFMQPmuyIAjCfzw9PeVcuXLJCQkJmrTBgwfLgHzjxg1ZlmW5V69esqmpqXzv3j2tfWfMmCED8rVr1zRpgDxmzBjN69atW8sGBgby/fv3tfatV6+ebGxsLL948UKWZVkeP368DMj79u17a33fLH/Dhg0yIB86dChV3k6dOsm2trZyfHy8Jm3atGmySqWS7969m+4xkpOT5Tx58silS5eWk5OTNemRkZGyra2tXLVqVU3aoUOHZEDesGHDW+udlqSkJDkxMVGuVauW3KRJk3fmd3JykiVJkv38/LTS69SpI5ubm8vR0dGyLMvylClTZJVKJfv6+mrl27hxowzIu3bt0qQBsp2dnRwREaFJCw0NlVUqlTxlyhRNWuXKleU8efLIsbGxmrSIiAjZ2tpafv2/lbt378qAvHTp0lT1f/O9W7p0qQxovRdOTk5yp06dUu3r6ekpe3p6al6ntHvDhg218g0YMEAG5P79+2ulN27cWLa2tk5V7ps6deokOzk5pap3RtooI1Le827duslly5Z9Z/5y5cppfd5kWZbnzZsnA/KVK1c0aW+2T79+/WRLS8u3lt21a1dZT09P9vf3TzfPzz//LAPymTNntNK///57WZIkOTAwUJblV+/Hm9/DNz8PT58+lQF5zpw5b61bWlI+L29+rt98zzLzGXz+/LlsaGiY6vt44sQJGdBqY0EQFKIrlCAIGt26dePp06ds374dgKSkJFatWkX16tUpUqQIADt27KBGjRrkyZOHpKQkzSOlm9SRI0fSLf/gwYPUqlULR0dHrfTOnTsTExOj6Vq0e/duihYtSu3atbPs3H788UfCwsLYsGEDAGq1mvnz51O/fv23ziITGBjIo0eP6NChAyrVqz+ZpqamNGvWjNOnTxMTE/NBdVqwYAHlypXD0NAQXV1d9PT0OHDgAAEBARnav2TJkpQpU0YrrW3btkRERHDhwgVAeb9KlSqFm5ub1vvl7e2dZneVGjVqaA2CtbOzw9bWlnv37gEQHR2Nr68vTZs21brLY2ZmRsOGDT+kGbJMgwYNtF4XL14cUO5mvZkeHh6eoe5QaXlXG73Nhg0bqFatGqamppr3fPHixRl6z7t06cLJkycJDAzUpC1dupSKFStSqlSpdPerVKkSL168oE2bNmzbto2nT5+myrN7925q1KihabO0HDx4kBIlSqQa09C5c2dkWebgwYPvPIfXWVtbU6hQIX799VdmzZrFxYsXtbpU5bRTp04RFxdHu3bttNKrVq2Kk5NTDtVKED5tIrAQBEGjefPmWFhYaLoz7dq1i8ePH2sN2n78+DH//PMPenp6Wo+SJUsCpHnRkuLZs2dpzriSJ08ezXZQxh/ky5cvy84LoGzZslSvXp0///wTUC64g4KC6Nev31v3S6lTevVWq9U8f/78vesza9Ysvv/+eypXrsymTZs4ffo0vr6+1K1bl9jY2AyVYW9vn25aSr0fP37M5cuXU71fZmZmyLKc6v2ysbFJVaaBgYGmTs+fP0etVr/12DnF2tpa67W+vv5b0981riY972qj9GzevJmWLVuSN29eVq1axalTp/D19aVr164Zqku7du0wMDDQjBfw9/fH19eXLl26vHW/Dh06sGTJEu7du0ezZs2wtbWlcuXK7Nu3T5MnI9+5jH5/M0qSJA4cOIC3tzfTp0+nXLly5M6dm/79+xMZGfleZX0MKefzKX7WBeFTJcZYCIKgYWRkRJs2bVi0aBEhISEsWbIEMzMzzaBogFy5cuHq6sqkSZPSLCPlIiMtNjY2hISEpEp/9OiRpmxQZmd58OBBZk4lTf3796dFixZcuHCBP/74g6JFi1KnTp237pNyEZlevVUqFVZWVu9dl1WrVuHl5cX8+fO10t/ngio0NDTdtJR658qVCyMjI5YsWZJmGSltnlFWVlZIkvTWY6dIuaMRHx+vlZ7RC1BDQ8NU+4ISvL5vvT8Fq1atokCBAqxbt05rXEta55gWKysrGjVqxIoVKzTjCwwNDWnTps079+3SpQtdunQhOjqao0ePMmbMGBo0aMCNGzdwcnLK0Hcuo9/f9N73tH50cHJyYvHixYAyq9r69esZO3YsCQkJLFiw4J3n9S6Z+QymfIfS+6x/jmucCMLHJu5YCIKgpVu3biQnJ/Prr7+ya9cuWrdujbGxsWZ7gwYNuHr1KoUKFaJChQqpHm8LLGrVqsXBgwc1FyIpVqxYgbGxsWb62Hr16nHjxo337lphYGAAkO4vx02aNCF//vwMHjyY/fv306dPn3cu6Obi4kLevHlZs2YNsixr0qOjo9m0aZNmpqj3JUmSpr4pLl++rDXT1Ltcu3aNS5cuaaWtWbMGMzMzzeD1Bg0acPv2bWxsbNJ8v9734sjExIRKlSqxefNmrV/ZIyMj+eeff7Ty2tnZYWhoyOXLl7XSMzILEiizQr25740bN7S6An1OJEnSLOaWIjQ0NMPtAUqA8OjRI3bt2sWqVato0qQJlpaWGd7fxMSEevXqMWLECBISEjTTttarV49Dhw69tW1r1aqFv7+/pptdihUrViBJEjVq1ADQfKbefO9Sulimp2jRoowcOZLSpUunOsaHysxnsEqVKhgaGrJ69Wqt9JMnT2ao25sgfI3EHQtBELRUqFABV1dX5syZgyzLqdauGD9+PPv27aNq1ar0798fFxcX4uLiCAoKYteuXSxYsCDdLhVjxozRjNEYPXo01tbWrF69mp07dzJ9+nQsLCwAZWrNdevW0ahRI37++WcqVapEbGwsR44coUGDBpoLmDel9DP/66+/MDMzw9DQkAIFCmh+edTR0aFv374MGzYMExOTdKeofJ1KpWL69Om0a9eOBg0a0KtXL+Lj4/n111958eIFU6dOzWjTamnQoAETJkxgzJgxeHp6EhgYyPjx4ylQoECGpu0F5e7Qd999x9ixY3FwcGDVqlXs27ePadOmaYKdAQMGsGnTJjw8PBg4cCCurq6o1Wru37/Pv//+y+DBg6lcufJ71X3ChAnUrVuXOnXqMHjwYJKTk5k2bRomJiaa2a5AuZBu3749S5YsoVChQpQpU4azZ8+muxDjmzp06ED79u3p06cPzZo14969e0yfPv2zXWugQYMGbN68mT59+mhmGJowYQIODg7cvHkzQ2V8++235MuXjz59+hAaGvrOblCgrPVgZGREtWrVcHBwIDQ0lClTpmBhYUHFihUB5Xu9e/duPDw8GD58OKVLl+bFixfs2bOHQYMGUaxYMQYOHMiKFSuoX78+48ePx8nJiZ07dzJv3jy+//57zWKQ9vb21K5dmylTpmBlZYWTkxMHDhxg8+bNWvW6fPky/fr1o0WLFhQpUgR9fX0OHjzI5cuX+fnnn9+zddOWmc+glZUVQ4YMYeLEiXTv3p0WLVoQHBysmYVNEIQ05OzYcUEQPkW//fabDMglSpRIc/uTJ0/k/v37ywUKFJD19PRka2truXz58vKIESPkqKgoTT7emHVFlmX5ypUrcsOGDWULCwtZX19fLlOmTJoztjx//lz+8ccf5fz588t6enqyra2tXL9+ffn69etvLX/OnDlygQIFZB0dnTRngwkKCpIBuXfv3u/VJlu3bpUrV64sGxoayiYmJnKtWrXkEydOaOV5n1mh4uPj5SFDhsh58+aVDQ0N5XLlyslbt25NcyaitDg5Ocn169eXN27cKJcsWVLW19eXnZ2d5VmzZqXKGxUVJY8cOVJ2cXGR9fX1ZQsLC7l06dLywIED5dDQUE0+QO7bt2+ax3pzdqbt27fLrq6usr6+vpw/f3556tSp8pgxY+Q3/1t5+fKl3L17d9nOzk42MTGRGzZsqHkP3jUrlFqtlqdPny4XLFhQNjQ0lCtUqCAfPHgw3Vmh3mz39GYOSqnnkydP0mteWZbTnxUqo22UlqlTp8rOzs6ygYGBXLx4cXnRokVpttvbDB8+XAZkR0dHrZnKUrzZPsuXL5dr1Kgh29nZyfr6+nKePHnkli1bypcvX9baLzg4WO7atatsb28v6+npafI9fvxYk+fevXty27ZtZRsbG1lPT092cXGRf/3111T1CAkJkZs3by5bW1vLFhYWcvv27eVz585pfScfP34sd+7cWS5WrJhsYmIim5qayq6urvLs2bPlpKSkt7ZBRmeFkuXMfwanTJkiOzo6yvr6+rKrq6v8zz//pGpjQRAUkiy/dm9fEAThCzd37lz69+/P1atXNQPOP0fOzs6UKlUqQwuzCYIgCEJ2EF2hBEH4Kly8eJG7d+8yfvx4GjVq9FkHFYIgCILwKRKBhSAIX4UmTZoQGhpK9erVs2S2GUEQBEEQtImuUIIgCIIgCIIgZJqYblYQBEEQBEEQhEwTgYUgCIIgCIIgCJkmAgtBEARBEARBEDJNDN5+B7VazaNHjzAzM3vnCr2CIAiCIAiC8CWRZZnIyEjy5MmDSvX2exIisHiHR48e4ejomNPVEARBEARBEIQcExwcTL58+d6aRwQW72BmZgYojWlubp7tx09MTOTff//l22+/RU9PL9uP/yURbZk1RDtmDdGOWUe0ZdYQ7Zh1RFtmDdGOWSOz7RgREYGjo6PmmvhtRGDxDindn8zNzXMssDA2Nsbc3Fx8qTJJtGXWEO2YNUQ7Zh3RlllDtGPWEW2ZNUQ7Zo2saseMDAkQg7cFQRAEQRAEQcg0EVgIgiAIgiAIgpBpIrAQBEEQBEEQBCHTxBgLQRAEQRCE/yQnJ5OYmJipMhITE9HV1SUuLo7k5OQsqtnXR7Rj1nhXO+rp6aGjo5MlxxKBhSAIgiAIXz1ZlgkNDeXFixdZUpa9vT3BwcFiDaxMEO2YNTLSjpaWltjb22e6nUVgIQiCIAjCVy8lqLC1tcXY2DhTF1hqtZqoqChMTU3fuaCYkD7Rjlnjbe0oyzIxMTGEhYUB4ODgkKljicBCEARBEISvWnJysiaosLGxyXR5arWahIQEDA0NxQVxJoh2zBrvakcjIyMAwsLCsLW1zVS3KPEuCYIgCILwVUsZU2FsbJzDNRGEnJHy2c/s+CIRWAiCIAiCIJCxBcAE4UuUVZ99EVgIgiAIgiAIgpBpIrAQBEEQBEH4ijk7OzNnzpxPtrzXBQYGYm9vT2Rk5EcpPy1hYWHkzp2bhw8fZtsxP1efVWBx9OhRGjZsSJ48eZAkia1bt75znyNHjlC+fHkMDQ0pWLAgCxYs+PgVFQRBEARB+MgaNmxI7dq109x26tQpJEniwoUL2Vwr8PX1pWfPnprXGb1my4gRI0bQt29fzMzMsqQ8Ly+vd14b2tra0qFDB8aMGZMlx/ySfVaBRXR0NGXKlOGPP/7IUP67d+/i4+ND9erVuXjxIsOHD6d///5s2rTpI9dUEARBEATh4+rWrRsHDx7k3r17qbYtWbIENzc3ypUrl+31yp0790cZCP/gwQO2b99Oly5dsqS88PBwTp48ScOGDd+Zt0uXLqxevZrnz59nybG/VJ9VYFGvXj0mTpxI06ZNM5R/wYIF5M+fnzlz5lC8eHG6d+9O165dmTFjxkeuqSAIgiAIwsfVoEEDbG1tWbZsmVZ6TEwM69ato1u3bgCcPHkSDw8PjIyMcHR0pH///kRHR6db7v3792nUqBGmpqaYm5vTsmVLHj9+rJVn+/btVKhQAUNDQ3LlyqV1bfZ6VyhnZ2cAmjRpgiRJODs7ExQUhEql4ty5c1plzp07FycnJ2RZTrNe69evp0yZMuTLl0+TtmzZMiwtLdmxYwcuLi4YGxvTvHlzoqOjWb58Oc7OzlhZWfHDDz+kWnV6586dlClThrx58/L8+XPatWtH7ty5MTIyokiRIixdulSTt3Tp0tjb27Nly5Z02034zAKL93Xq1Cm+/fZbrTRvb2/OnTuX6em0ssvJkxKBgVY5XQ1BEARB+KrIMkRH58wjnevqVHR1denYsSPLli3TuhjfsGEDCQkJtGvXjitXruDt7U3Tpk25fPky69at4/jx4/Tr1y+d85Zp3Lgx4eHhHDlyhH379nH79m1atWqlybNz506aNm1K/fr1uXjxIgcOHKBChQpplufr6wvA0qVLCQkJwdfXF2dnZ2rXrq114Z6Sp3PnzunOUHT06NE0jxMTE8Pvv//O2rVr2bNnD4cPH6Zp06bs2rWLXbt2sXLlSv766y82btyotd/27dtp1KgRAKNGjcLf35/du3cTEBDA/PnzyZUrl1b+SpUqcezYsTTrJii+6AXyQkNDsbOz00qzs7MjKSmJp0+fprm6YHx8PPHx8ZrXERERgDKvb3YHI/Hx0KOHDjdveuDvn8TkyYnkzp2tVfiipLx/n0tQ+akS7Zg1RDtmHdGWWeNrbsfExERkWUatVqNWqwHlAt/c/EN/f1UBlh9cn4gINSYmGcvbuXNnfv31Vw4ePEiNGjUApRtUkyZNsLCwoH///rRp04b+/fsDUKhQIebMmUONGjX4888/MTQ0BNCc/759+7h8+TK3b9/G0dERgOXLl1O6dGnOnDlDxYoVmTRpEq1atdIac1C6dGlN271eXsqCg+bm5tja2gLKgm1du3alT58+zJgxAwMDAy5duoSfnx8bN27UlJMSLKWUFRQURLly5bSOo1arSUxM5M8//6RQoUIANGvWjFWrVhESEoKpqSnFihXDy8uLgwcP0qJFC0C53tu7dy8jR45ErVZz7949ra5j+fPn15SfIk+ePPj5+WmlfQ7ebMe0qNVqZFkmMTEx1QJ57/M34YsOLCD1vLwpjZteNDxlyhTGjRuXKv3ff//N9oVzoqN1cXQszc2b+Vm+XJdNmxJo3z6AOnWCyMSiiF+9ffv25XQVvgiiHbOGaMesI9oya3yN7airq4u9vT1RUVEkJCQASmCRmeAgMyIiInij10668uTJQ6VKlfjrr78oX748d+/e5dixY2zevJmIiAjOnTvHnTt3WLNmjWaflAvMK1eu4OLiglqtJi4ujoiICPz8/MibNy8WFhaaH1fz5cuHhYUFFy9exMXFBT8/P9q1a6fZ/qbXy0sRGxur9bpmzZro6OiwZs0amjVrxsKFC6levTrW1tapyk2ZASql+9br2+Pi4jA2NiZ37tyadEtLS/Lnz49ardakWVtb8+jRI83rffv2YWVlhZOTExEREXTs2JFOnTpx7tw5atSoQf369alcubJWPVQqFZGRkeme96fubTNpJSQkEBsby9GjR0lKStLaFhMTk+FjfNGBhb29PaGhoVppYWFh6OrqaiLoN/3yyy8MGjRI8zoiIgJHR0e+/fZbzM3NP2p909K4cSK//36MNWuqceWKPgsWlMHXtzS//66mYsUM3isVACXi3rdvH3Xq1EFPTy+nq/PZEu2YNUQ7Zh3Rllnja27HuLg4goODMTU11fyCb2am3Dn4ELIsExkZiZmZ2QctPGZsbM777NajRw/69+/PwoUL2bhxI05OTjRs2FBz7J49e/LDDz+k2i9//vzo6+ujUqkwNDTE3NwcAwMDdHR00rzmMTIywtzcHCMjI03+tLxe3pv7vq5Dhw6sW7eOdu3asWnTJmbNmqWV5812tLW1JTY2ViuPoaEhenp6qdIMDAy00lLOMyXtwIEDNG7cWPO6WbNmeHh4sHPnTs22Pn368Ouvv2rKiI6Oxs7OLkeuBzMjI5/HuLg4jIyM8PDw0HwHUrxPIPVFBxbu7u78888/Wmn//vsvFSpUSPePpoGBAQYGBqnS9fT0cuwPbfHi4Zw5k8z//qdi5Eg4f17FN9+o6N4dpkyBdGIkIR05+V5+SUQ7Zg3RjllHtGXW+BrbMTk5GUmSUKlUqFSvuj996IymSpcqMDWVtMr7WFq3bs3AgQNZu3YtK1asoEePHpruLOXKlcPf35+iRYu+tYyU8y9ZsiT379/n4cOHmq5Q/v7+vHz5kpIlS6JSqXB1deXQoUOaweFvKw+Uz5Qsy6naokePHpQqVYoFCxaQmJhI8+bNtfKkdNtJKats2bIEBARo5Ul5/npaysXzm2kp5ciyzI4dO1ixYoVWHjs7O7p27UrXrl1ZuHAhP/30EzNnztRsv3btGl5eXtnynmalN9sxLSqVCkmS0vz+v8/fg8+qZaKiovDz88PPzw9QppP18/Pj/v37gHK3oWPHjpr8vXv35t69ewwaNIiAgACWLFnC4sWLGTJkSE5UP1N0deGHHyAwEDp2VAZ2LVoERYvCX3/BZ9bdTxAEQRCELGJqakqrVq0YPnw4jx49onPnzpptw4YN49SpU/Tt2xc/Pz9u3rzJ9u3b07yDAVC7dm1cXV1p164dFy5c4OzZs3Ts2BFPT0/NwOkxY8bw999/M2bMGAICArhy5QrTp09Pt37Ozs4cOHCA0NBQrelaixcvTpUqVRg2bBht2rTByMjorefp7e3NqVOnUs3u9L7Onz9PdHQ0Hh4emrTRo0ezbds2bt26xbVr19ixYwfFixfXbI+JieH8+fOpJgUStH1WgcW5c+coW7YsZcuWBWDQoEGULVuW0aNHAxASEqIJMgAKFCjArl27OHz4MG5ubkyYMIHff/+dZs2a5Uj9s4K9PSxfDkePQunSEB4OvXpBlSrwxqxtgiAIgiB8Jbp168bz58+pXbu2ZuAxgKurK0eOHOHmzZtUr16dsmXLMmrUqDQnsIFXi9lZWVnh4eFB7dq1KViwIOvWrdPk8fLyYsOGDWzfvh03Nzdq1qzJmTNn0q3bzJkz2bdvH46OjppruNfrnZCQQNeuXd95jj4+Pujp6bF///535n2bbdu2Ub9+fXR1X3Xc0dfX55dffsHV1RUPDw90dHRYu3at1j758+enevXqmTr2F08W3urly5cyIL98+TJHjp+QkCBv3bpVTkhISLUtMVGWZ8+WZTMzWQZZliRZ7t1blp89y/56fg7e1pZCxol2zBqiHbOOaMus8TW3Y2xsrOzv7y/HxsZmSXnJycny8+fP5eTk5Cwp70s2ceJEuVSpUmluS6sd//zzT/nbb7/N1DFLly4tr1u37r32qVixorx69epMHTenZOTz+LbvwPtcC39WdywEbbq6MGCA0j2qXTule9SCBUr3qMWLRfcoQRAEQRA+TVFRUfj6+jJ37lzNVLgZ0bNnTzw8PN46w9HbJCQk0KxZM+rVq5fhfcLCwmjevDlt2rT5oGN+TURg8QVwcIBVq+DwYShZEp49g+7doWpVuHAhp2snCIIgCIKgrV+/fnzzzTd4enpmqBtUCl1dXUaMGIHZB46s19fXZ8yYMe+1v62tLUOHDv2gGb6+NiKw+IJ4esLFizBzJpiawpkzUKEC9O0LL17kdO0EQRAEQRAUy5YtIz4+nnXr1qVakE34fInA4gujpweDBindo9q0UbpHzZunDO6+ezenaycIgiAIgiB8qURg8YXKkwfWrIGDByFfPiXQcHcXM0cJgiAIgiAIH4cILL5wNWrA6dPg6gqPHyvdpXbuzOlaCYIgCIIgCF8aEVh8BfLmhWPHoE4diImB775TFtUTBEEQBEEQhKwiAouvhLm5cqeic2dlGtpevWDECGUMhiAIgiAIgiBklggsviJ6erBkCYwZo7yePBk6dICEhJytlyAIgiAIgvD5E4HFV0aSYOxYZQE9HR1YvRrq1hXT0QqCIAiCkPPGjh2Lm5vbe+1z+PBhJEnixX8XM8uWLcPS0lIrz19//YWjoyMqlYo5c+akmyZkjggsvlJduypdo0xN4dAh+OYbCA7O6VoJgiAIgvA+OnfujCRJqR63bt3K6arlmFatWnHjxg3N64iICPr168ewYcN4+PAhPXv2TDNNyDwRWHzFvL2VQd0ODnDtmrLWxaVLOV0rQRAEQRDeR926dQkJCdF6FChQ4IPKSsim/tGJiYkfrWwjIyNsbW01r+/fv09iYiL169fHwcEBY2PjNNM+xMc8j8+RCCy+cm5uynS0JUvCo0dQvTrs25fTtRIEQRAEIaMMDAywt7fXeqSsZn3kyBEqVaqEgYEBDg4O/PzzzyQlJWn29fLyol+/fgwaNIhcuXJRp04dBg8eTMOGDTV55syZgyRJ7HxtvnoXFxcWLlwIgK+vL3Xq1CFXrlxYWFjg6enJhQsXtOooSRILFiygUaNGmJiYMHHiRACmTp2KnZ0dZmZmdOvWjbi4uHee765duyhatChGRkbUqFGDoKAgre2vd4VatmwZpUuXBqBgwYJIkpRmWkoZ//zzD+XLl8fQ0JCCBQsybtw4rfZK7zwyst///vc/mjRpgrGxMUWKFGH79u1a9b527Rr169fH3NwcMzMzqlevzu3btzXbly5dSvHixTE0NKRYsWLMmzfvnW2V3URgIZA/Pxw/Dl5eEBkJPj6wbFlO10oQBEEQco4sy8QkJH3wIzYh+YP3lbNoysaHDx/i4+NDxYoVuXTpEvPnz2fx4sWai+EUy5cvR1dXlxMnTrBw4UK8vLw4duwYarUaUIKTXLlyceTIEQBCQ0O5ceMGnp6eAERGRtKpUyeOHTvG6dOnKVKkCD4+PkRGRmodZ8yYMTRq1IgrV67QtWtX1q9fz5gxY5g0aRLnzp3DwcHhnRfLwcHBNG3aFB8fH/z8/OjevTs///xzuvlbtWrF/v37ATh79iwhISG0aNEiVZqjoyN79+6lffv29O/fH39/fxYuXMiyZcuYNGnSW88jo/uNGzeOli1bcvnyZXx8fGjXrh3h4eGa98rDwwNDQ0MOHjzI+fPn6dq1qyY4WbRoESNGjGDSpEkEBAQwefJkRo0axfLly9/aXtlNN6crIHwaLC1hzx5l7MWaNdClC9y7B6NHKwO+BUEQBOFrEpuYTInRe3Pk2P7jvTHWz/gl2o4dOzA1NdW8rlevHhs2bGDevHk4Ojryxx9/IEkSxYoV49GjRwwbNozRo0ejUim/LxcuXJjp06dr9ndwcCAyMpKLFy9Srlw5jh07xpAhQ9i8eTMAhw4dws7OjmLFigFQs2ZNrfosXLgQKysrjhw5QoMGDTTpbdu2pWvXrprXbdq0oWvXrnTv3h2AiRMnsn///rfetZg/fz4FCxZk9uzZSJKEi4sLV65cYdq0aWnmNzIywsbGBoDcuXNjb28PkGbapEmT+Pnnn+nUqROg3M2YMGECQ4cOZUzKlJppnEeHDh0ytF/nzp1p06YNAJMnT2bu3LmcPXuWunXr8ueff2JhYcHatWvR09MDoGjRopp9J0yYwMyZM2natCkABQoU0AQxKcf9FIjAQtAwMICVK8HJCaZMUWaPun8fFixQpqoVBEEQBOHTU6NGDebPn695bWJiAkBAQADu7u5Ir/1CWK1aNaKionjw4AH58+cHoEKFClrlWVhY4ObmxuHDh9HT00OlUtGrVy/GjBlDZGQkhw8f1tytAAgLC2P06NEcPHiQx48fk5ycTExMDPfv39cq983jBAQE0Lt3b600d3d3Dh06lO65BgQEUKVKFa1zcnd3f2v7ZNT58+fx9fXVutOQnJxMXFwcMTExmnEYb55HRvdzdXXVbDcxMcHMzIywsDAA/Pz8qF69uiaoeN2TJ08IDg6mW7du9OjRQ5OelJSEhYVFFpx51hGBhaBFpVLWt8ifH/r2Vda9ePgQNmwAM7Ocrp0gCIIgZA8jPR38x3t/0L5qtZrIiEjMzM00dwXe99jvw8TEhMKFC6dKl2VZ6wI8JQ3QSk8JRF7n5eXF4cOH0dfXx9PTEysrK0qWLMmJEyc4fPgwAwYM0OTt3LkzT548Yc6cOTg5OWFgYIC7u3uqgeBpHed9ZVU3sbSo1WrGjRunuSvwOkNDQ83zN88jo/u9GTRIkqTpbmZkZPTWeoHSHapy5cpa21LG0nwqRGAhpKl3b8iXD1q1gr17wcMDDhwAa+ucrpkgCIIgfHySJL1Xd6TXqdVqkvR1MNbX/aDAIquUKFGCTZs2aQUYJ0+exMzMjLx58751Xy8vLxYvXoyuri61a9cGwNPTk7Vr12qNrwA4duwY8+bNw8fHB1DGQTx9+vSd9StevDinT5+mY8eOmrTTp0+/85y2bt2qlfaufTKqXLlyBAYGphmkfYz9Xufq6sry5ctJTExMFYDY2dmRN29e7ty5Q7t27T74GNlBDN4W0tWgARw+DLa24OenvI6OzulaCYIgCIKQEX369CE4OJgffviB69evs23bNsaMGcOgQYPeGfB4eHgQGRnJP//8g5eXF6AEG6tWrSJ37tyUKFFCk7dw4cKsXLmSgIAAzpw5Q7t27d76C3yKH3/8kSVLlrBkyRJu3LjBmDFjuHbt2lv36d27N7dv32bQoEEEBgayZs0almXRjDOjR49mxYoVjB07lmvXrhEQEMC6desYOXLkR9nvdf369SMiIoLWrVtz7tw5bt68ycqVKwkMDASUhQOnTJnCb7/9xo0bN7hy5QpLly5l1qxZmTrnrCYCC+GtKlZU7lRYWsKpU9CiBYgpmwVBEATh05c3b1527drF2bNnKVOmDL1796Zbt24ZuuC1sLCgbNmyWFtba4KI6tWro1arte5WACxZsoTnz59TtmxZOnToQP/+/bXWkUhPq1atGD16NMOGDaN8+fLcu3eP77///q375M+fn02bNvHPP/9QpkwZFixYwOTJk995rIzw9vZmx44d7Nu3j4oVK1KlShVmzZqFk5PTR9nvdTY2Nhw8eJCoqCg8PT0pX748ixYt0ty96N69O//73/80U+V6enqybNmyD16v5GOR5I/ZWe0LEBERgYWFBS9fvsTc3Dzbj5+YmMiuXbvw8fFJc0BPdjl5EmrXhthYaN8eli9XxmN8Tj6VtvzciXbMGqIds45oy6zxNbdjXFwcd+/epUCBAlp94j+UWq0mIiICc3PzHO0K9bkT7Zg1MtKOb/sOvM+1sHiXhAypWhU2bgQdHVi1CgYPBhGSCoIgCIIgCClEYCFkmI8PLF2qPJ8zB9KZMloQBEEQBEH4ConAQngvHTpAyjihX36B//0vZ+sjCIIgCIIgfBpEYCG8t4EDlaACoFcv2LIlZ+sjCIIgCIIg5DwRWAgfZNIk6NYN1Gpo00aZllYQBEEQBEH4eonAQvggkgQLFkDjxhAfD999Bxcv5nStBEEQBEEQhJwiAgvhg+nqwt9/g6cnREZC3bpw61ZO10oQBEEQBEHICSKwEDLF0BC2bQM3NwgLA29vCAnJ6VoJgiAIgiAI2U0EFkKmWVjAnj1QqBDcuQP16sGLFzldK0EQBEEQBCE7icBCyBJ2dvDvv2BvD5cuQaNGyirdgiAIgiB8/pydnZkzZ05OVyOVw4cPI0kSL97zF01Jkti6dSsAQUFBSJKEn5+fZvuJEycoXbo0enp6NG7cON00QZsILIQsU7CgcufCwgKOHoXWrSEpKadrJQiCIAhfrs6dOyNJkuZhY2ND3bp1uXz5ck5X7bPh6OhISEgIpUqV0qQNGjQINzc37t69y7Jly9JNE7SJwELIUmXKwD//KGMvtm+Hnj1BlnO6VoIgCILw5apbty4hISGEhIRw4MABdHV1adCgQU5XK0slJCR8tLJ1dHSwt7dHV1dXk3b79m1q1qxJvnz5sLS0TDftfX3M8/gUiMBCyHLVq8O6daCjA0uXvlpMTxAEQRCErGdgYIC9vT329va4ubkxbNgwgoODefLkiSbPsGHDKFq0KMbGxhQsWJBRo0aRmJioVc727dupUKEChoaG5MqVi6ZNm6Z7zKVLl2JhYcG+ffv4559/sLS0RK1WA+Dn54ckSfz000+a/L169aJNmzYAPHv2jDZt2pAvXz6MjY0pXbo0f//9t1b5Xl5e/PDDD4wYMQJbW1vq1KkDwK5duyhatChGRkbUqFGDoKCgd7bPzZs38fDwwNDQkBIlSrBv3z6t7a93hUp5/uzZM7p27YokSSxbtizNNAB/f398fHwwNTXFzs6ODh068PTpU63z6NevH4MGDSJXrlya88jIfv3792fo0KFYW1tjb2/P2LFjter94sULevbsiZ2dHYaGhpQqVYodO3Zotp88eRIPDw9MTEwoWbIkP/74I9HR0e9sr8wQgYXwUXz3HSxapDyfNg1mzszZ+giCIAjCe5FlSIj+8EdizIfvm4lb/VFRUaxevZrChQtjY2OjSTczM2PZsmX4+/vz22+/sWjRImbPnq3ZvnPnTpo2bUr9+vW5ePEiBw4coEKFCmkeY8aMGQwZMoS9e/dSp04dPDw8iIyM5OJ/C1odOXKEXLlyceTIEc0+hw8fxtPTE4C4uDjKly/Pjh07uHr1Kj179qRDhw6cOXNG6zgrVqxAR0eHY8eOsXDhQoKDg2natCk+Pj74+fnRvXt3fv7557e2h1qtpmnTpujo6HD69GkWLFjAsGHD0s2f0i3K3NycOXPmEBISQosWLVKltWrVipCQEDw9PXFzc+PcuXPs2bOHx48f07JlS60yly9fjq6uLidOnGDhwoXvtZ+JiQlnzpxh+vTpjB8/XhMUqdVq6tWrx8mTJ1m1ahX+/v5MnToVHR0dAK5cuYK3tzdNmzbFz8+PJUuWcOLECfr16/fW9sos3XdnEYQP06ULPH0KQ4fCkCHKwO527XK6VoIgCIKQAYkxMDnPB+2qAiwzc+zhj0DfJMPZd+zYgampKQDR0dE4ODiwY8cOVKpXvx+PHDlS89zZ2ZnBgwezbt06hg4dCsCkSZNo3bo148aN0+QrU6ZMqmP98ssvLF++nMOHD1O6dGkALCwscHNz4/Dhw5QvX57Dhw8zcOBAxo0bR2RkJNHR0dy4cQMvLy8A8ubNy5AhQzRl/vDDD+zZs4cNGzZQuXJlTXrhwoUZP3485ubmqFQqhg8fTsGCBZk9ezaSJOHi4sKVK1eYNm1aum2zf/9+AgICCAoKIl++fABMnjyZevXqpZk/pVuUJElYWFhgb28PgImJSaq0KVOmUK5cOSZPnqzZf8mSJTg6OnLjxg2KFi2qOY/p06dr8owePTpD+7m6ujJmzBgAihQpwh9//MGBAweoU6cO+/fv5+zZswQEBGjyFyxYUFPer7/+Stu2bRkwYABqtRo7OzvmzJlDjRo1mD9/PoaGhum2WWaIwEL4qH76SVnfYsYM6NYNXFwgnR9ABEEQBEH4ACkXiwDh4eHMmzePevXqcfbsWZycnADYuHEjc+bM4datW0RFRZGUlIS5ubmmDD8/P3r06PHW48ycOZPo6GjOnTundRELStedw4cPM2jQII4dO8bEiRPZtGkTx48f58WLF9jZ2VGsWDEAkpOTmTp1KuvWrePhw4fEx8cTHx+PiYl2MFW+fHmt1wEBAVSpUgVJkjRp7u7ub61zQEAA+fPn1wQVGdkno86fP8+hQ4c0Qd3rbt++rbngf/POT0b3c3V11drm4OBAWFgYoLxf+fLl0+RNq263bt1i9erVmjRZllGr1dy9e5fixYu/x5lmnAgshI9u2jS4cUMZzN2kCZw7p0xPKwiCkF1kWSZJLROfpCY+MZnYx0+Iu3mTxMIuxBsYo6+jwjnpJTG7dqLv7Ix53bpa+0qSBGo1JMdDUhwkxin/Jv33OjkBrAqAae4cPEshS+kZK3cOPoBarSYiMhJzMzOtuwbvdez3YGJiQuHChTWvy5cvj4WFBYsWLWLixImcPn1aczfC29sbCwsL1q5dy8zX+ikbGRm98zjVq1dn586drF+/PlUXJC8vLxYvXsylS5dQqVSUKFECT09Pjhw5wvPnzzXdoEAJUGbPns2cOXMoXbo0JiYmDBgwINXA5jcDDfkDuoiltc/rgUlmqNVqGjZsmOYdEwcHB83zN88jo/vp6elpbZMkSTOO5V3vl1qtplevXvTv3x+1Wk1UVBSmpqaoVCry58//7pP7QCKwED46lQpWroTKleH6dWjeHA4cAH39nK6ZIAifs/DoBA5eD+PQ9cfcvK9ixcOzJCTLxCclE5+kJi4xGVVMNI5h9yAxgbN2xUFKQqUfxl+7FpE3MpLpjRy4UfglCboJVAuU6bU1mVB7iaNBP2GnVmObnEShzTJ6LyXMq7zEzjYWPSAxRkVUiCH6pkmY2L12MWTpBPkqgmMlyFcB7EqDrvhj91mSpPfqjqRFrQa9ZGX/DwksMkmSJFQqFbH/LSh14sQJnJycGDFihCbPvXv3tPZxdXXlwIEDdOnSJd1yK1WqxA8//IC3tzc6Ojpag7NTxlnMmTMHT09PJEnC09OTKVOm8Pz5c3788UdN3mPHjtGoUSPat28PKBfBN2/efOev6CVKlNCsPZHi9OnT79zn/v37PHr0iDx5lK5tp06deus+GVWuXDk2bdqEs7Oz1oxSH2u/17m6uvLgwQOtrlNvHuPatWsULlxYCXQjIjRdyj4mEVgI2cLcHLZuhUqV4PhxGDgQ/vwzp2slCMLnJuhpNPv8H7PP/zHn7oWj1vwYqaL4HT+KvAjmnF0xHplao9J/SsXwC4w9eoD7VoZcdbdCpf8MSVLzIE8yqjBQ6z0mQl/5jzbIAg65SoRZSGwyUsoEfX6PTcI+BgbkyUWgo4RVcjLfXFfTwVfiib2Mr6sOuZAo8yKMAlcfo39nG4ZWG5EkQMcA8rgpwUa+Csq/FvnSOjVB+GDx8fGEhoYC8Pz5c/744w+ioqJo2LAhoPTxv3//PmvXrqVixYrs3LmTLVu2aJUxZswYatWqRaFChWjdujVJSUns3r1bMwYjhbu7O7t376Zu3bro6uoycOBA4NU4i1WrVvHbb78BSrDRokULEhMTNeMrUuqzadMmTp48iZWVFbNmzSI0NPSdgUXv3r2ZOXMmgwYNolevXpw/f/6d60nUrl0bFxcXOnbsyMyZM4mIiNAKsDKjb9++LFq0iDZt2vDTTz+RK1cubt26xdq1a1m0aJFmIHVW7fc6T09PPDw8aNasGbNmzaJw4cJcv34dSZKoW7cuw4YNo0qVKvTt25du3bohyzLBwcEcOHCAuXPnZsn5p0UEFkK2cXGBNWugYUOYNw/KloXu3XO6VoIgfMrUahm/By/Y5/+Y/f6PuRkWpdmmo06mRF4rKhWWCQ49QavAAzgGPGR9gVNsKRFBspzE49wyjy7CQ7t4dPTDQJIwS1ZzsF4ihRMT+VbWpa9hWWzyuXMnXyIBLhE8i4ygYHQETxKjSNCNY3yLaCxjogm2jQPguY4Ot8xUnC+s5qGNxCpjJTCRDG1ZtFGNebRMfFt7XA3uoop9DsFnlEcKszyvgox8FZXAQ+/d3VAEIT179uzRdKExMzOjWLFibNiwQXMx36hRIwYOHEi/fv2Ij4+nfv36jBo1Smv6Ui8vLzZs2MCECROYOnUq5ubmeHh4pHm8atWqsXPnTnx8fNDR0aF///6AMtbjwoULmuNaWVlRokQJHj16pBU0jBo1irt37+Lt7Y2xsTE9e/akcePGvHz58q3nmT9/fjZt2sTAgQOZN28elSpVYvLkyXTt2jXdfVQqFVu2bKFbt25UqlQJZ2dnfv/9d+q+1t3xQ+XJk4cTJ04wbNgwvL29iY+Px8nJibp16771zsCH7vemTZs2MWTIENq0aUN0dDSFCxdm6tSpgHJH48iRI4wYMQJPT09kWaZQoUK0atUq0+f9NpL8IR3WviIRERFYWFjw8uVLrUFO2SUxMZFdu3bh4+OTqq/d52rSJBg5UukKdfgwZNEYqnf6EtsyJ4h2zBqiHdMXl5jMiVtP2R/wmP0BYTyJjNds01VJeOYxpMOVnVgHnGHRLyU5HHYSgIZn1Lg8kDnoKnGhiApjSY/CaigU9YLCCQkUTkykcEIiuU3zILn4gEs9cKqWblel6PgkLj94ycXg51y8/4IL958RHvsCSTcKSTcSSScSSTcSE+MYzM2ikOKu0Wl3NEUeyvzwvQ7WprbUsq2Iz/kXONwKxsrxOQaJgSAnax9IpQt2pcD5GyjfBXIVTrM+H9vX/JmMi4vj7t27FChQIEtmy8nOridfMtGOWSMj7fi278D7XAuLOxZCths+HC5ehE2boFkzZTB3ng+b0U8QhC9EyniJff6hHL3xlNjEVxffZga6eLrkpk4JO74pYsWZhwcwWLUPvReJxB05jlRcBweVPXJDJ5Jjo+j2OJApwUE4JCWjGaLpUAZcfJSHfWml//w7mBjo4l7IBvdCyloAsizz4HksF+4rgcbF4Bf4P3rJi3CZFwBSY+Z+E0ShvDcxlC/wJPYJa+/tovjuJAwfwME25SjQZTIVk3XQeXAeHvgiPfCF6DAI8VMep/6AIt5Q5Xso6JWhegqCIHwqRGAhZDtJgmXLIDAQrl5VBnMfOgQGBjldM0EQspMsy/xzOYRVp+69MV4C8lgYUruEHXVcbCh524+okxs57OpCm92rCYkOoUItNYnGRhT75luGhz/D4doeDG+/1t1IpQcFPaBYfeXORBaMa5AkCUdrYxytjWnklhdQ7q5ce/SSE7eesebMfUKfFuHc0yLo69SlaunnmNsEcMR9Py8vR7PM+hLhh/pjaWBJ24gSVF/3ENvWQ7Ht4Q3BZ+HKRrixB27uVR65iysBhmtL0VVKEITPgggshBxhaqoM5q5QAU6dgn794K+/xI9zgvC1CAyNZPS2q5y5G65JK+FgTp0SdtQpYUfJPOZIkkRI8HUe/fwTOonJbDfSIcRRwtrQmsrNW9IqIgKr43MhMRoA2cAcqci3UMwHCtcGQ4uPfh6GejqUd7KmvJM133sVYvfVUBYfv8ul4Bcc9rMBvqFKwfpE+0RQQ/bl4P0DPI9/TtLBY+g8lNl4+A8eFg/iW6dvcW+1Ar0nd5AuLIaLq+FJAPzTH/aPhQpdoWJ3MHd4V5UEQRByjAgshBxTqBCsXQs+PvC//0H58tC7d07XShCEjykyLpE5+2+y7GQQyWoZQz0VvT0L0bx8PvJZGZP4OIzYi6e4aVyQ5deWs+vuLlqWV5OoI6HrlJ8xlbvSUDLHYM9weHYTAHW+ypw28KRiiwHoGX7g9KBZQE9HxXdl8vBdmTxcuP+cJcfvsvtqKKfvvOT0HXCy8aCTezsK53/CSac9LN6/l+vmUdy7vZ3tt7fjHGfKxKWJ2Hbuin3/y0hX1sKZhfDyPhybASfmQMmmyl2MvOVy7DwFQRDSIwILIUd5e8OUKTBsGPzwA5QsCdWr53StBEHIarIss83vEZN2BWgGY3uXtGNUgxLks1IWA0t48IBbdeuiltX0+V7FczPlFmZg60p0LtmZkWYFUf07Cvy3KoWa5IY6E0gu0Ywnu3eDzqezXkS5/FaUa2vFoxexrDh1j7/P3ufesxgm7AjEzECXlhVb0W/gEJ4mBrLv3j7239tPpaMh6L+Q8d2ykDgvG5pU6YVe5d4QuAtOz4f7J+HKeuXhWEUJMIo1AB3xX7kgCJ8G8ddIyHE//QQXLsC6dcp4i/PnIZ+Y5l0QvhjXQyMYve0aZ//r9uRsY8zY70ri5WKLnJREojqRPXf3sPzacto4JCPJYB4nUam0N51KdKK0lYsyqPloG0iMAUkFlXqC1y9gZAmJiTl7gm+Rx9KIn+sVo3+twmy+8JClJ+5y+0k0i4/fZemJu9QpYUeXaj35qcJP7CzzD6tWzOSa6Qtun5nIMv/l9C3Zi28eGmPeZRdSiB+cXgBXN0HwaeVh4ai0RbkOYGSV06crCMJXTgQWQo6TJFi8WFmV+9IlaNIEjh2DLJjxTxCEHBQRl8icfTdZfupVt6cfahahe/UC6OuoeLpkCcEbVjGiPQQnPQHgtzam+JRqxoLi7clnlg9uHYC1neHZLaXQ/O7g86sys9NnxFhfl/ZVnGhbKT9Hbz5hyYkgjt54wt5rj9l77TElHMzp4VGRUWMPsOnWRv66/BfBkcEc+nM4Bf9Vc7eKK2WWrkVquhDqjAPfxXBuMbwMhn2j4PBUcGsD1X4Ey/w5fbqCIHylRGAhfBJMTF4N5j53ThlrsXSpGMwtCJ8jWZbZ6veQSTuv8zRK6fZUt6Q9IxsU13R7inwawr2FczF+GYeLr4rYqra0K96OFkVbYGFgAS+CYV0HCNiuFGpiC99OANdWn/UfBpVKwsvFFi8XW24+jmTpySA2X3iAf0gEA9ddYuUpSyY2bsjupk1YFbCK4AsLiNWPZZXFVZ7u6UT/sv2pYF8Bao6A6oPhygalm1TYNfD9H/itAc9h4N4XdL6utSgEQch5IrAQPhnOzkp3KG9vWL4cypWD/xbzFAThMxEQEsGYbdc4G6R0eyqYy4Sx35XEo2huTZ7A8ECGHBuCcf0EHMN1Kd6lH9NKdUFfRx+S4uHYTDg6479uTzpKV58av2TLLE/ZqYidGZOblGaotwurz9xn/uHbXLj/goZ/HKdrNWcG1O5K0vRWrDzxByeCNxMTdpEue7vQPK4ULS8ZU/CnkRiU6wBl28Pdo3BkGtw7AfvHwOV1UH8WOGXTCqSCIAiAWMZQ+KTUqgW//qo8HzRIWd9CEIRPX0RcIuP+uUaDucc5GxSOkZ4OP3m7sHtAdTyK5kZWq3n6v/+xc8uvtNvVjqCIIJ4Wt6ftL8vpWaaXElTc2g/z3OHAeCWoyO8OvY5CvalfXFDxOktjffrWKMz+QZ7UL+1Aslpm0bG71J51hNO3YulbYzj/tNhNy6It0ZV0KbXRDw6eZPek3gS9DFLu4BT0hM47ofF8MLaBMH9YWhe29YOY8HdVQRByhLOzM3PmzHmvfTp37kzjxo01r728vBgwYIDmdUxMDM2aNcPcXJmy+sWLF2mmCR+HCCyET86AAdC+PSQnQ4sWEBSU0zUSBCE9siyz6fwDas44wtITyliKeqXs2T/Yk741CmOgqwNA6JJFPJkxE4vJS1BFx1E9b3U2NtxIObty/3V7ag+rmkH4baXbU5O/oMtusC+Vw2eYfewtDPmzXTmWdq6Io7URIS/j6LXyPD1WnCMh3pRR7qPY1ngbN7t4craoxOwyD2m8rTFjT47lUchNkiMjwa0t9DsH5ToqhV5cCXPLK+tiyPLbKyB8tkJDQ/nhhx8oWLAgBgYGODo60rBhQw4cOJClx3nzIv5TsHnzZiZMmKB5vXz5co4dO8bJkycJCQnBwsIizTTh4xBdoYRPjiQpi+X5+yuzRTVpAidOgLFxTtdMEITXhUXE0e/vi5rZntLq9gQQ8CyA4SZb6WEH+8vp8n3VgXQq1RmVpIKzi+DfUZAUq3R7qtwLvH7+ou9QvEuNYrb8W9CTPw7d5K+jd9gfEMaJW8/4sXYRun1TgJ/bLiCwbiC+F+dy5MERNt3chOW8TdQIUGE7/BccmrWG7+aCWzvYMVC5e7GtD/itVrpH2RbL6VMUslBQUBDVqlXD0tKS6dOn4+rqSmJiInv37qVv375cv349W+sjyzLJycno6mbPJaa1tbXW69u3b1O8eHFKlSr11rT3lZycjCRJqFTiN/m3Ea0jfJKMjGDLFsidG/z8oHt38WObIHxKbj+Joun8k5y9q3R7Glr3VbcnAFmtJur4cdZdX0f7Xe25lfCAOX3z0vGXlXQp3RWVDPw7EnYNUYIKp2rQ+xjUnfJVBxUpjPR1+Mm7GLv6V6dSAWtiE5OZuvs6DX4/jm9QOC7WLvxR6w9W1FtBeZuyFAlOQj86gQnXf+fog6NKIfmrKF3J6owHPWNl/MWCarB/HCTE5OwJClmmT58+SJLE2bNnad68OUWLFqVkyZIMGjSI06dPa/K9fPmSnj17Ymtri7m5OTVr1uTSpUua7WPHjsXNzY2VK1fi7OyMhYUFrVu3JjIyElC6IB05coTffvsNSZKQJImgoCAOHz6MJEns3buXChUqYGBgwLFjx7h9+zaNGjXCzs4OU1NTKlasyP79+9/r3JKTkxkxYgTW1tbY2NgwdOhQ5DcuBl6/i+Ll5cXMmTM5evQokiTh5eWVZhpAQkICQ4cOJW/evJiYmFC5cmUOHz6sKXfZsmVYWlqyY8cOSpQogYGBAffu3cvwfnv37qV48eKYmppSt25dQkJCtOq9ZMkSSpYsiYGBAQ4ODvTr1y/D79WnTAQWwicrf37YuBF0deHvv2HmzJyukSAIABfuP6f5/JM8eB6Ls40xu3+sTh+vV92e5KQk7vboTnD3Hvy7YjwJ6gS88nmxodEm3GzdICkBtvSCk3OVAmuOUsYH2JXMuZP6RBWxM2NdzyrMaFEGaxN9Ah9H0mLBKYZtvMzz6ATK2pZlaf3lmK9YwF/d83IsXyR9D/Rl7MmxRDx5qMwMVe1H6HsGitYDdRIcnwXzKsONf3P69D5psiwTkxjzwY/YpNgP3vfNi+f0hIeHs2fPHvr27YuJSepV5y0tLTXnUr9+fUJDQ9m1axfnz5+nXLly1KpVi/DwV2Nwbt++zdatW9mxYwc7duzgyJEjTJ06FYDffvsNd3d3evToQUhICCEhITg6Omr2HTp0KFOmTCEgIABXV1eioqLw8fFh//79XLx4EW9vbxo2bMj9+/cz/B7MmjWLVatWsWjRIo4fP054eDhbtmxJN//mzZvp0aMH7u7uhISEsHnz5jTTALp06cKJEydYu3Ytly9fpkWLFtStW5ebN29qyouJiWHKlCn873//49q1a9ja2mZ4vxkzZrBy5UqOHj3K/fv3GTJkiGb7/Pnz6du3Lz179uTKlSts376dwoULv9d79akSXaGET5qHB8yZA/36KatzV6gA//3YIAhCDjgQ8Ji+ay4Ql6imTD4LFneuSC5TA608/i8DOaLyp6ouGCfq8FOFIXQo0QFJkiA+UhlPceew0vWp0R/KuAAhXZIk0bx8PmoVs2Xanuus9Q1m3blg/vUPZbhPcZqXz0d1J08qDqiMw8XfWem/kl1XNlJn0EbMK1ahxJQ56Fjmh7Zr4fpO2DUUXtyHNS2g+HdQdypY5M3p0/zkxCbFUnlN5Rw59pm2ZzDWe3f/31u3biHLMsWKvb1726FDh7hy5QphYWEYGCjf1xkzZrB161Y2btxIz549AVCr1SxbtgwzMzMAOnTowIEDB5g0aRIWFhbo6+tjbGyMvb19qmOMHz+eOnXqaF7b2NhQpkwZzeuJEyeyZcsWtm/frvXr/Nv89ttvDBw4kGbNmqFSqViwYAF79+5NN7+1tTXGxsbo6+tr1fHNtNu3b/P333/z4MED8uTJA8CQIUPYs2cPS5cuZfLkyQAkJiYyb948zXm8z34LFiygUKFCAPTr14/x48drtcXgwYP58ccfNWkVK1YEMv5efapEYCF88vr0AV9fZQraNm2UrlF2djldK0H4+qw9e5/hW66glsHLJTd/ti2HiYHy34icnIw6Pp5197Yy49wM1O4JnCrnwE/N5+Ca21UpIPIxrG4OoZdBzwRaroAitXPwjD4vVib6TG3mSvPy+Rix5SqBjyP5aeNlNpx/wKTGpShiZ8bQikPxyufF+kWDsHz5jCe+J5h7cS7fVx2EgY4BFKsPBTzh8BRl/YuA7XD7INQYAeW65PQpCu8p5c6G9I61Xc6fP09UVBQ2NjZa6bGxsdy+fVvz2tnZWRNUADg4OBAWFpahulSoUEHrdXR0NOPGjWPHjh08evSIpKQkYmNjM3zH4uXLl4SEhGguuAF0dXWpUKFChu/opOfChQvIskzRokW10uPj47XaSF9fH1dX1/fez9jYWBNUgHY7hoWF8ejRI2rVqpVm3TL6Xn2qRGAhfPIkCf78Uwku/P2VGaP27AEdnZyumSB8HWRZ5rcDN5mzX7nV36J8PiY3LY2ejtKbNunpU+4PGUxAwj2mfPsUJImazrUYX228stgdwNNbsKqJ8ku5cS5otwHylsupU/qsVXC2Zkf/b1hy/C5z9t/k7N1w6v12jJ4eBfmhZhEqOVSixM97WOw0lCMPj3LzzhqOhJ9l0jeTKG5RFMnAFLwnQZk2yuDuB2dh7y/o+q3B0qJpTp/eJ8NI14gzbc980L5qtZrIyEjMzMw+aLCvka5RhvIVKVIESZIICAjQmoI1rfo4ODhojQVIkdJdCkBPT3tRRUmSUKvVGarLm12xfvrpJ/bu3cuMGTMoXLgwRkZGNG/enISEhAyV9zGp1Wp0dHQ4f/48Om9cTJiammqeGxkZaQVtGd0vrXZMCYaMjN7+3mb0vfpUicBC+CyYmMCGDVCxIuzfD5MmwejROV0rQfjyJSWrGbXtKn+fDQagX43CDP62qNZ/ttcDjiP7niWPChwr6dPOeyhti7V9lefBOVjdAmLDwaoAtN8ENoXSOpyQQXo6Knp5FqK+qwNjt19jf0AY8w7fZp//Y+a1K0cROzN+7DQP1/uHGHtqLLde3GLGnNb0OWVOsTnzMS1VWpnKt+teuLAc9o9BenwFj8dXUZ9IAo8h8JXPfiNJUoa6I6VFrVaTpJuEsZ7xR51FyNraGm9vb/7880/69++f6uL+xYsXWFpaUq5cOUJDQ9HV1cXZ2fmDj6evr09ycnKG8h47dozOnTvTpEkTAKKiogh6j/njLSwscHBw4Ny5c9SrVw+ApKQkzZiDzChbtizJycmEhYVRvXr1j77f68zMzHB2dubAgQPUqFEj1faseq9yytf9V0P4rJQoAfPnK8/HjoWDB3O0OoLwxYtNSKb3qgv8fTYYlQQTGpdiiLeLJmCQZZlV/qvoEDSO+T4q5vRxYHr71bQr3u5VUBG4B5Y1UIKKPGWh2z4RVGShfFbGLOpYgYUdypPbzICbYVF898cJNl94AECN/DXY0mgLtR1r0fxoIiYPnrF+bj/uvryrFKBSQYUu0O886pJNkZDROTxJGX8R/SznTkzIsHnz5pGcnEylSpXYtGkTN2/eJCAggN9//x13d2Xl9dq1a+Pu7k7jxo3Zu3cvQUFBnDx5kpEjR3Lu3LkMH8vZ2ZkzZ84QFBTE06dP33o3o3DhwmzevBk/Pz8uXbpE27ZtM3z3I0X//v2ZM2cOW7Zs4fr16/Tp0ydLFrcrWrQo7dq1o2PHjmzevJm7d+/i6+vLtGnT2LVrV5bv96axY8cyc+ZMfv/9d27evMmFCxeYO1eZzCKr3qucIgIL4bPSsSN07apMPdu2LYSG5nSNBOHL9Dw6gXb/O83+gMcY6KqY3748Hao4abZHnzrF/GO/Ms13GknqJAzrezO321ZK5XptnvgLK2BtW2U62cK1odMOMM2dxtGEzJAkCe+S9uzqX51qhW2ITUxm0PpLDNt4mbjEZKwNrZlVYzby7DHsrWLAH5We0fKflqwOWI1a/u9CzzQ3yY3/4mL+7si6hsoq6Au+gfun335wIccVKFCACxcuUKNGDQYPHkypUqWoU6cOBw4cYP5/v8ZJksSuXbvw8PCga9euFC1alNatWxMUFITdewxaHDJkCDo6OpQoUYLcuXO/dbzE7NmzsbKyomrVqjRs2BBvb+/3vtMwaNAgWrduTdeuXXF3d8fMzExzBySzli5dSseOHRk8eDAuLi589913nDlzRmumq6zc73WdOnVizpw5zJs3j5IlS9KgQQPNrFJZ9V7lFEnO7AiYL1xERAQWFha8fPkSc3PzbD9+YmIiu3btwsfHJ1Wfva9VTAxUrgxXr0LNmvDvvxkbbyHaMmuIdswan3I7BofH0GnpWe48icbCSI/FnSpQwfnVIlRRx09wr3cv7lsnM66tDr2/GUKnkp1e3aWQZTj6KxyapLwu0xa++12Z+vQj+JTbMrslq2XmHrzJbwduIstQzN6Mee3KUTC30v87NDqUUSdGcTpECRhGHrahSs325G/fjaSkJKUdKzijt7kbPLupzNxVewy4//BFd42Ki4vj7t27FChQAENDw0yXp1ariYiIwNzcXCyolgmiHbNGRtrxbd+B97kW/uzepXnz5mlOunz58hw7dizdvCmLtrz5yO5VKIWsZWysjLcwMVG6Q02YkNM1EoQvx7VHL2k6/yR3nkSTx8KQjb3dtYIKgF2Rp4gwSCbEWqK3+yA6l+r8KqhITlIGBKcEFdUHQ+N5Hy2oELTpqCQG1C7Kyq6VyWWqz/XQSBrOPc72S48AsDexZ2GdhQyvPJyKQbq4nnpM5OSZ7Dmy+NVMO7YloOchKN0C5GTYNxrWtoGYT38OfUEQctZnFVisW7eOAQMGMGLECC5evEj16tWpV6/eO6cuCwwM1CzmEhISQpEiRbKpxsLHUqwYLFigPB8/XhnQLQhC5py49ZRWC0/zJDKeYvZmbO5TjSJ2Zlp51l5fy4Sw5QzvpEPiqL50LtP11caEGFjfAc4vBSTwmQG1RitTuwnZ6psiudjZvzqVC1gTnZBM/78vMnLrFeISk1FJKtoUa8OoHzayv2Fe1nmoGHrvN4YcG0K0OlopwMAMmi6CBrNBxwBu7IGFHspAfEEQhHR8VoHFrFmz6NatG927d6d48eLMmTMHR0dHTR/C9Nja2mJvb695vDlFmPB5at8eundXel20awchITldI0H4fG3ze0jnpWeJik+iSkFr1vVyx97i1e3w2GvX2HlwIZPOKHciGn/Tg57l+rwqICYcVjSCwF3KhWjLFVCpR3afhvAaO3NDVnevTN8aymD5Vafv02z+Se49U4KHAtaF+H7aHvL3HYCuSpdDDw6xNHQOV2ePQ05OVgLCCl2h+z6wLggvg2FJXTg1T/nDKwiC8IbPZrrZhIQEzp8/z88//6yV/u2333Ly5Mm37lu2bFni4uIoUaIEI0eOTHN6rxTx8fHEx8drXkdERABKH97ExMRMnMGHSTlmThz7czBzJpw+rcvVqxJt2qjZvTsZ3XQ+1aIts4Zox6zxKbXj4hNBTN1zAwCfUnZMb1YaA91XdYu/dYugzh2xSY4hbzsdPKu14/tS35OUlKQU8DIY3b9bIj27iWxoQXKLVcj53SGbzu1TastP0YCahSjnaMGQjVe49iiC+r8fZ0qTktQtqQwE7Vy8M+727ow6NoK2a25ieG8TRx/cwX3GMqWLW64S0GU/OjsHoLq+Hfb+gjroOMkNfgdDixw+u6yRmJiILMuo1er3nrkoLSndylLKFD6MaMeskZF2VKvVyLJMYmJiqh/g3+dv62czePvRo0fkzZuXEydOULVqVU365MmTWb58OYGBgan2CQwM5OjRo5QvX574+HhWrlzJggULOHz4MB4eHmkeZ+zYsYwbNy5V+po1azA2/rD5rIWP6+FDUwYP9iQuTpeWLQNp21aMoRGEjFDLsO2eisMhys1rT3s1jZ3VqN7ouXTz+XmKL9tIsiSzs1Ml6lk20YypMI+5j/vtGRgmvSBWz5pThYYQaZQvu09FyIDn8bD8pg53I5X3zsNeTSMnNbr/9V1IkBO4cXYJNfcGMb6NDrZ5y9PQqCF60n/jY2SZAk/3U+rhGlRyMtH6ufEt0I+XxgVy6Iyyjq6uLvb29jg6OqKvr5/T1RGEbJeQkEBwcDChoaGvfjT6T0xMDG3bts3Q4O3PLrA4efKkZl5mgEmTJrFy5coMD8hu2LAhkiSxffv2NLendcfC0dGRp0+f5tisUPv27aNOnTpf/Wwnb7N2rUTHjrpIksyOHcnUqZP6Yy3aMmuIdswaOd2Osiwzcps/688/BGCYd1G6VXPSWvgO4PjD4ww6Ngj9mETq5a/LL7UmoZL+uxINvYLuqu+Q4iORcxcnqfU6MM+T3aeS4235OUlMVjNr/y3+dzwIANe85vzWqgz5rIxITEzk33//5Zn9I36/sRC1rKaUTSmmu47C3uHV2ETp0UV0NndDenkfWUcfde0JqMt3/azH0sTFxREcHIyzs3OWzAoly7Jm5e03v1NCxol2zBoZace4uDiCgoJwdHRMc1aoXLlyZSiw+Gy6QuXKlQsdHR1C31i4ICws7L3m9a1SpQqrVq1Kd7uBgQEGBgap0vX09HL0P6ycPv6nrkMHOHECFi6U6NxZFz8/yJPO9Y1oy6wh2jFr5FQ7zj98m/XnH6KSYGbLMjQpq32XITEkhEvndjHkxTyS1EnULlaPUdWnoqP67xZ5RAisbwfxkZDfHanNWvSMLLP9PF4nPpPvpqcHIxuUpErBXAzecInLDyNoNO8UM1u64VXEGkmS6Fi+B8XzuzH06FCe3bhC2MjmPG/bjNJDxiGpVOBUCXofha19kQJ3orN3GDoPTkPD38Ew+3+AywrJyclIkoRKpcqSaU1TupuklCl8GNGOWSMj7ahSqZAkKc2/o+/zd/WzeZf09fUpX748+/bt00rft2+fVteod7l48SIODg5ZXT3hEzB7NpQpA0+eQJs28MadPEEQ/rPnagjT9ih3ecc0LJkqqEgKD+dGh7YYDJtByRtx1HCsweTqk18FFQkxyvSjkY8gV1FosxZyOKgQ3k/tEnbs7P8NZRwtiYhLoseKc0zdE0jyf92vq+apyt/1/8Yn2BrjOJk7/25io//aV1PSGllB69XgPRlUunBtC/zlBaFXcuycBEHIeZ9NYAHKCoz/+9//WLJkCQEBAQwcOJD79+/Tu3dvAH755Rc6duyoyT9nzhy2bt3KzZs3uXbtGr/88gubNm2iX79+OXUKwkdkZKSsb2FqCkePwpgxOV0jQfj0XH7wggHr/ADo5O5Ep6rOqfIExN/jnPkzws3ArnRFZnjOQE/13y9WajVs6QmPLoKRNbRdJ4KKz1Q+K2M29HKnazVljMTiE/eY66/Dk0ilO7CjmSM9p+/hSJcyzGiqYvz5KYw7NY6E5ASlAEkC977QZQ+Y54Pw27CoFvityalTEgQhh31WgUWrVq2YM2cO48ePx83NjaNHj7Jr1y6cnJwACAkJ0VrTIiEhgSFDhuDq6kr16tU5fvw4O3fupGnTpjl1CsJHVqQI/O9/yvPJk2Hv3pytjyB8SkJextJ9+TniEtV4ueRmVIMSqfJcD79Or8N9mdVQzabBFZjQdAH6Oq8NZj04HgL+AR19aL1GmYZU+Gzp66oY3bAEC9qXw8xQl7uREs0XnuF6qDIjorGeMb2G/k2X6gORkNh0cxNzxjfkwaFdrwpxrAi9j0ERb0iOh63fw/5xShAqfFGcnZ2ZM2dOpspIWbz4xYsXWVKnoKAgJEnCz88vS8pLT+fOnWncuHGmyxk7dixubm6ZLudT9VkFFgB9+vQhKCiI+Ph4zp8/rzW707Jlyzh8+LDm9dChQ7l16xaxsbGEh4dz7NgxfHx8cqDWQnZq1Qq+/1553r49PHiQs/URhE9BdHwS3ZadIywyHhc7M+a2KYuuzqv/ApKjormx9n/0/LcnkQmRlLEvx9QmCzHUfW0Q38VVcHy28vy7P8DJHeHLULeUA5t7Vya3ocyjl3E0n3+Kw4FhgNIvu1vpbsyvPR/XJ0bU23Cfl30Gc+noplcFGFsrXeI8flJeH58FGzsr3eaEbHHy5El0dHSoW7duTldFw8vLiwEDBmilVa1alZCQECwssm+q4jt37tCmTRvy5MmDoaEh+fLlo1GjRty4ceOjHleSJLZu3aqVNmTIEA4cOPBRj5uTPrvAQhAyYtYsKFsWnj4V4y0EIVkt8+Pai/iHRJDLVJ//daqAmeGrwXhyQgK3enYheexMqh19RkmbkvxZ60+M9V6bYjvoOPwzQHnu8ROUaZW9JyF8dM42JgwslUwlZyui4pPousyX5SeDNNur5a3G5E5ruFTWnJPFJToHTWDDjQ2vClCpoOZIaLwAVHrgvw2W1YfIx9l/Ml+hJUuW8MMPP3D8+HGt3hufGn19fezt7bNtlqeEhATq1KlDREQEmzdvJjAwkHXr1lGqVClevnyZLXV4nampKTY2Ntl+3OwiAgvhi2RoCOvXg5kZHD8Oo0bldI0EIedM2RXA/oAw9HVVLOxQAUdr7TV5HsaHsd0qiBgDiCrpxMI6CzHTN3uV4dltWNce1IlQojF4Dc/eExCyjYkeLO1Unubl86GWYcz2a4zdfo2k/0Z1O+UuTJOlB7ne91uS5GTGnxrPhONjiQ0NeVWIWxvouE0Z4P3oAiyqCaFXc+iMvg7R0dGsX7+e77//ngYNGrBs2TKt7Sndjw4cOECFChUwNjamatWqWmuA3b59m0aNGmFnZ4epqSkVK1Zk//796R6za9euNGjQQCstKSkJe3t7lixZQufOnTly5Ai//fYbkiQhSRJBQUFpdoU6ceIEnp6eGBsbY2Vlhbe3N8+fPwdg//79eHh4YGlpiY2NDQ0aNOD27dsZbht/f3/u3LnDvHnzqFKlCk5OTlSrVo1JkyZRsWJFTb4rV65Qs2ZNjIyMsLGxoWfPnkRFRaVbblrdwtzc3Bg7dqxmO0CTJsq6Pymv3+wKpVarGT9+PPny5cPAwAA3Nzf27Nmj2Z7S1Wvz5s3UqFEDY2NjypQpw6lTpzLcBtlJBBbCF6twYViyRHk+dSrs3i3mwBa+PmvO3Od/x+8CMKNFGco7WWltD40Opfu/3VlRKZbZgwsytutKLAxe66IQEw5rWkLsc8hbHposUH6ZFr5Y+roqfm3uytC6LgAsOxlEjxXniIpXbv2a6Jswo+Zs+pftj4SEwV/rudrwWx6dOviqEOdq0P0A2BSGiAewxBtu/JsTp5Np6pgY1DExvL7sl5yQoKQnJKSd97XxJXJiopL+2hpZb8v7IdatW4eLiwsuLi60b9+epUuXktYyZSNGjGDmzJmcO3cOXV1dunbtqtkWFRWFj48P+/fv5+LFi3h7e9OwYcN07350796dPXv2EBLyKqjctWsXUVFRtGzZkt9++w13d3d69OhBSEgIISEhODo6pirHz8+PWrVqUbJkSU6dOsXx48dp2LAhycnJgLI424ABA/D19eXAgQOoVCqaNGmS4ZW4c+fOjUqlYuPGjZoy3xQTE0PdunWxsrLC19eXDRs2sH///kxN9uPr6wvA0qVLCQkJ0bx+02+//cbMmTOZMWMGly9fxtvbm++++46bN29q5RsxYgRDhgzBz8+PokWL0qZNm1QL2X0KxP8OwheteXNI+bvQpYsOT55kfuEjQfhcnLj1lNHblF+KB9YuyndlXi3uIssyD3dtoeee7jyMeoijmSOzmi/Fxui1W/RJCbC+Izy7BRaO0Ppv0DPK7tMQcoAkSfTxKsy8duUw0FVxKPAJzeef5OGLWM32Hq49+KPaLNzuqTCNTGLW7pFcenLpVSE2haD7fnCuDglR8HcrOLMwh87owwWWK09gufIk//cLOsCzJUsILFeexxMmaOW9Ue0bAsuVJ+m1i+3na9YQWK48ISNGauW9Vas2geXKk/Dar+8vtmz5oDouXryY9u3bA1C3bl2ioqLS7Mc/adIkPD09KVGiBD///DMnT54kLi4OgDJlytCrVy9Kly5NkSJFmDhxIgULFkx3QeGqVavi4uLCypUrNWlLly6lRYsWmJqaYmFhgb6+PsbGxtjb22Nvb4+Ojk6qcqZPn06FChWYN28eZcqUoWTJkvTr149cuXIB8N1339G0aVOKFCmCm5sbixcv5sqVK/j7+2eobfLmzcvvv//O6NGjsbKyombNmkyYMIE7d+5o8qxevZrY2FhWrFhBqVKlqFmzJn/88QcrV67k8eMP68qXO3duACwtLbG3t9e8ftOMGTMYNmwYrVu3xsXFhWnTpuHm5pbqbsiQIUOoX78+RYsWZdy4cdy7d49bt259UN0+JhFYCF+8GTOgfHkID5eYNauCGG8hfBVuhUXRe9V5ktQyjd3y0L9WYa3tz9avI2LQcFouuUMeI3sWf7sYW2PbVxlkGXYOgqBjoG+qDMw1y/hipMKXwae0A+t7uZPbzIDroZE0+uMEfsEvNNs9Ctem6LqNrGnjwN5CkXTZ04Vtt7a9KsDICtpvhrIdQFbD7qGwcwgkiz/EWSUwMJCzZ8/SunVrAHR1dWnVqhVLUm7Zv8bV1VXzPGVNr7AwZZB+dHQ0Q4cOpUSJElhaWmJqasr169ffOl6je/fuLF26VFPOzp07te6CZETKHYv03L17l3bt2lGwYEHMzc0pUECZHvl9xpH07duX0NBQVq1ahbu7Oxs2bKBkyZKatdECAgIoU6YMJiYmmn2qVauGWq3W6i6W1SIiInj06BHVqlXTSq9WrRoBAQFaaW977z4lIrAQvngGBsp4C3NzmYAAG8aPFx974csWHp1A12W+RMYlUd7JiqnNXFMNlNzzcD/xuhDkbMiiuotxMH1j4dCTv8PFlSCpoPkSsC+VjWcgfErKOFqytW81itmb8TQqnlYLT7Hryqtf5J3ti/Hz8H+o6ViTRHUiEw6NYM/PHUiOVe5uoKsP382FOuMBCXwXKXcv4iJy5oTek8uF87hcOI+O1atuhDZdu+Jy4Tx2bwzgK3riOC4XzqP72kK8Vm3b4nLhPA6TJmrlLXxgPy4XzqNfqJAmzbJJk/eu3+LFi0lKSiJv3rzo6uqiq6vL/Pnz2bx5s2acQorXV1BO+ZuQ0qXop59+YtOmTUyaNIljx47h5+dH6dKlSXiju9frOnbsyJ07dzh16hSrVq3C2dmZ6tWrv1f9jYzefhe0TZs2PHv2jEWLFnHmzBnOnDkD8NZ6pcXMzIzvvvuOSZMmcenSJapXr87Eicp7IstyuoPJ00tXqVSpupslfmBXtjePkVZ93vbefUrEFZbwVShYEObPV/pWTpum4i3j0QThsxaflEyvlee4Hx5DPisjFnYoj6GedveDPXf3MM3mDEO66+AxbBb5zfNrFxKwA/b9t8Kk92Qo6p1NtRc+VXktjdj4fVVquOQmPklNn9UX+PPQLc2FlYmeCbNrzKZbqW7026HGaes5DnRpQKL6vwstSYJqP0KrlaBrBLf2K+MuXny6sxelUBkbozI21rrQk/T1lXR9/bTzvjYOSdLTU9INDDKU930kJSWxYsUKZs6ciZ+fn+Zx6dIlnJycWL16dYbLOnbsGJ07d6ZJkyaULl0ae3t7goKC3rqPjY0NjRs3ZunSpSxdupQuXbpobdfX1093XEMKV1fXdKdfffbsGYGBgYwYMYJatWpRvHjxVMHSh5AkiWLFihEdHQ1AiRIl8PPz07wGZUC5SqWiaNGiaZaRO3durfElERER3L17VyuPnp7eW8/f3NycPHnycPz4ca30kydPUrx48fc+r0+BCCyEr0aLFjLffhuELEu0bw8f2G1SED5Zsizzy6Yr+AY9x8xAl6WdK5LL1EBr+52nNxhzUgkaGnr0wCO/l3Yhj/xgcw9AhgrdoHLvbKu/8GkzNdBlUccKdP5vtfZf9wby08bLJCQpv5qqJBUDyg8gV6fOhJvCfNfH9N3fl6iE12bWKd4QuuwCU3sI81dmjHpwLgfO5suwY8cOnj9/Trdu3ShVqpTWo3nz5ixevDjDZRUuXJjNmzdrApO2bdtm6Bfx7t27s3z5cgICAujUqZPWNmdnZ86cOUNQUBBPnz5Ns7xffvkFX19f+vTpw+XLl7l+/Trz58/n6dOnWFlZYW1tzaJFi7h16xYHDx5k0KBBGT4nULpaNWrUiI0bN+Lv78+tW7dYvHgxS5YsoVGjRgC0a9cOQ0NDOnXqxNWrVzl06BA//PADHTp0wM4u7S6gNWvWZOXKlRw7doyrV6/SqVOnVGNInJ2dOXDgAKGhoekGRD/99BPTpk1j3bp1BAYG8vPPP+Pn58ePP/74Xuf5qRCBhfBV6dbtCiVLyjx+DB06iIVhhS/LvMO32XzxIToqiT/blaOInZnW9rAVy7jTqiWmT6KpYFeBvm59tQuIeAR/t4bEGChUE+pNV35pFoT/6OqoGPtdScY3KolKgo3nH9Bh8RmeR7/qltKg6VCS1//BQydjToWcotOeToS8fPiqkLzloMdBsCsN0U+UtS6ubs6Bs/n8LV68mNq1a6e52FyzZs3w8/PjwoULGSpr9uzZWFlZUbVqVRo2bIi3tzflypV75361a9fGwcEBb29v8uTJo7VtyJAh6OjoUKJECXLnzp3muIiiRYvy77//cunSJSpVqoS7uzvbtm1DV1cXlUrF4sWLuXDhAqVKlWLgwIH8+uuvGTqfFPny5cPZ2Zlx48ZRuXJlypUrx2+//ca4ceMYMWIEAMbGxuzdu5fw8HAqVqxI8+bNqVWrFn/88Ue65f7yyy94eHjQoEEDfHx8aNy4MYVe69YGMHPmTPbt24ejoyNly5ZNs5z+/fszePBgBg8eTOnSpdmzZw/bt2+nSJEi73WenwpJTms+MkEjIiICCwsLXr58ibm5ebYfPzExkV27duHj46PVv054fylt6ezsg7u7HrGxMHky/PJLTtfs8yI+k1kjq9tx5+UQ+q5RLiAmNC5FhypOWtvVsbFcrFEV4xdxrPUxo9/EneQ2fm2WkoRoWFIXQi9D7mLQ7V8wzL6VcTNDfCazxvu24+HAMPqtuUhUfBIFcpmwpHNFCuR6Nfj12tNr9D3QF8KeMnYt2P/yC8UatHtVQHwUbOoGN/6bs7/mSKg+JEeC2bi4OO7evUuBAgUwNMz87IFqtZqIiAjMzc1RfeHTM8fExJAnTx6WLFlC06ZNs7Tsr6kdP6aMtOPbvgPvcy0s3iXhq1OiBPz5p/J81Cg4cSJn6yMImeUX/IJB6/0A6FLNOVVQAbDtwR4Gt0tk4zcqGvz0h3ZQoVbD5p5KUGFsA23XfTZBhZBzvFxs2fR9VfJaGnH3aTRN5p3g9J1nmu0lc5Vkdf3VdLhgit2zZO7/OplTwa/9wTUwhdZroMp/d84OToSt30NSPMKnT61W8+jRI0aNGoWFhQXfffddTldJ+ASIwEL4KnXuDO3aQXIytGkD4eE5XSNB+DAPX8TSffk54pPU1HDJzcj6JVLlCQwPZNKZSTwzl7DvP4CKDpW0M+wfA9d3gI6+cqFn5Zw9lRc+ey72ZmztWw03R0texCTSYfEZNl94oNme1zQvzebu5KyXPZObSfQ51I+tt7a+KkClA3UnQ/1ZIOnApb9hZRNlQUbhk3b//n3y5s3L+vXrWbJkCbq6ujldJeETIAIL4askSTB/PhQpAsHB0LWrMm2/IHxOouKT6LbMl6dR8RSzN2Nu23LoqLS7kYT+vYrZq/sSnxxP9bzV6Va6m3Yh55crU8sCNPoT8lfJptoLX4rcZgas7VmF+q4OJCbLDFp/iQVHbmtmjLI0taHNn3upVMaHJDmJUSdGsWrzWO1Vqyt2g3YbwMAc7p2AJfXg5YN0jih8CpydnZFlmeDg4LeuQyF8XURgIXy1zMxg3TrQ14dt22Du3JyukSBkXLJapv/fF7keGkkuUwMWd66IqYH2L4bRFy7wbMJk+ix4iFt0LiZ/MxmV9Nqf/bvHlEXwADyHgWvLbDwD4UtiqKfD3NZl6eVREICpu68zfoc/arUSXOjr6DPVYyrdSnWj8EOZUqPXcbh1HeIjX74qpHAt6LoXzPLAkwBY/C2EXc+J0xEE4QOJwEL4qpUtq6zMDfDTT5DByTMEIcctPn6Hg9fDMNBV8b9OFchrmXqRqX/UFzlXGE4XV/FT8zlYGlq+2hj9TBk4q06CUs3AS8xiIGSOSiXxi09xRtZX5t9feiKI/msvEp+kzOOfMh1tjwJtkSUIiXvCj8cHa09Ha1dCmTggV1GIeKisdXH/dLadg5jPRvhaZdVnXwQWwlevXz9o3BgSEqBVK4iMzOkaCcLbXQ+NYMbeGwCM/a4kbo6WqfJcfnKZaQF/MKOpCtPRQ3G1LfNqoyzDzoEQ9Vi5gGv0p5hWVsgy3asX5LfWbujpSOy4HPLfKvCvViT2aTOcmLkjWdDChBNhZ+i0pxOh0aGvCrB0VO5c5KsEcS9gRSO4vuuj1jllFqyYmJiPehxB+FSlfPYzO7OeGGkjfPUkCRYvVu5W3LoFvXvDqlXiOkv4NMUnJTNw3SUSktXULm5L64qOqfI8vXWNwX6DSVIn8a2zN21Kd9TOcHk9+G8DlS40/Qv0Ut/tEITMaOSWF2sTfXqvPM+JW89o/ddplnapiK2ZMo1lNa92LCjlRt8Dfbnx/AYLRzemlc9PFKvVTCnA2Bo6boONXZTpaNe1gwZzoHyn9A+aCTo6OlhaWhIWFqYc/o2Vtt+XWq0mISGBuLg4MU1qJoh2zBpva0dZlomJiSEsLAxLS8tUi/y9LxFYCAJgbQ1//w0eHrBmDdSqpQzoFoRPzex9NwkIicDaRJ8pTV1TXfxEHj/O45498KoicapBAcZVHaed50Uw7PpJee45DPKkvWiTIGRW9SK5WdvTnS7LznLtUQTN5p9kRdfKmrUuUqajnf1nR1rufETCnpGcWSxRucp/ayHoG0Or1bDjR7i4Cv7pr9xl8/jpo/zyY29vD6AJLjJDlmViY2MxMjLKVIDytRPtmDUy0o6Wlpaa70BmiMBCEP5TtSpMnKgsmNevH1Spoqx5IQifCt+gcBYevQ3A5CalyW1mkCrPyV3/I78arGJ1mOk1C1N901cb1WplnYD4l5C3AnwzKLuqLnylSuezYNP3Vem45Cz3nsXQbP5JlnauSJn/uu/lNc3LyN5rOHy+Cbf0X7A6cDxjcqloXLixUoCOLnz3B5g5wNFf4dAkiAwBnxnKVLVZSJIkHBwcsLW1JTEx8d07vEViYiJHjx7Fw8NDLNqYCaIds8a72lFPTy/TdypSiMBCEF4zdCgcOgT//quMtzhzBoyNc7pWgqBMLTtovR+yDM3L56NuqdS/LJ0NOcvQYhdxa66iSetRuFi7aGc4swCCjoGesdIFSkf8FyB8fE42JmzsXZWuy3y58vAlbRadZn778ngWVRZptLSwo96qA4w+MZqk+3sYdWIUT6PC6Fq6GyodHeXuRM2RYGqn3G07twSiwqDZYtDL/CrZb9LR0cn0RZaOjg5JSUkYGhqKC+JMEO2YNbKzHUWHNUF4jUoFK1aAvT1cvQoDBuR0jQRBMXGHP8HhseS1NGJMw9S30p7EPGHo0aGoZTWOdZvQuNQbU8eGXYf9Y5Xn304Am0Ifv9KC8J/cZgb83bMK1YvkIiYhmW7LfNly8dU6FQb6RkzxmkaXUl1AlkmYPIf9Pb8jOeG1Vbgr9YCWy5WFHK/v+G8hvRfZfzKCIKRLBBaC8AY7u1eDtxctUta6EISctN//MWt9g5EkmNmyDGaG2r84vTiwn0O9mhIV8ZQiVkUYUWWEdgFJCbClJyTHQ+HaUOGNRfIEIRuYGuiyuFNFGrnlIUktM3DdJf76r2sfKNPRDio/iLE2HfG4IpPn5B1mrexDQvJrC+mVaAQdtigL6d0/CUvrQcSjHDgbQRDSIgILQUhDrVowfLjyvEcPuH377fkF4WN5FhXPz5svA9CjekGqFLTR2q6OiSHol58o7fuURhd0mek5EyPdN2Z5OjodQi6BkZXSX10MghRyiL6uitkt3ej+TQEAJu+6zoTXFtIDaNZwKGFjurKovi4rdM/S90BfohOjXxXi/A102Q2m9hDmD/+rA08Cs/tUBEFIgwgsBCEdY8fCN98o61q0bq2scyEI2UmWZX7ZfIWnUQm42JkxqE7RVHmOPfNlcsNEfItIVBw0kQIWBbQzBPvCsZnK8wazwdwhG2ouCOlTqSRGNijBCB9lIb3Fx+8yYJ0fCUlqTZ6arX+i1cCFGOkacTrkNN9v6UhYUMCrQuxLQfd9YFMEIh4oq3TfP5PdpyIIwhtEYCEI6dDVVaagtbaGc+fg559zukbC12bj+Qf86/8YPR2J2a3cMNTTHlD6MOohw48PJyC/xIOR7albpIF2AQnRShcoWQ2lW0LJJtlYe0F4ux4eBZnTyg1dlcT2S4/ousyXqPgkzfaqeauyxHsJtipLGv/lz61WLbh35cSrAizzKwvp5a3waiG9wN3ZfyKCIGiIwEIQ3iJfPli2THk+ezb880+OVkf4igSHxzDuH38ABtYpSok85lrbo65eYeSuAUQkRFDKphRDKgxJXci/IyH8DpjnBZ9fs6PagvBeGpfNy5LOFTHW1+H4rae0/usUTyJfDdgulasU/6syG5s4XfTjkhl+cCgBz167c2FiA522QxFvSIqFte3gwoocOBNBEEAEFoLwTg0bvpodqnNnuH8/J2sjfA2S1TKDN1wiKj6JCk5W9PLQnsFJHR3Nzd7d6DHtKiWfGTPTayb6Ovrahdzcp0zLCdB4HhhZZk/lBeE9eRTNzdqeVbAx0efqQ2UhvXvPXo2pKFCkAsXWbWZljwJctoygy94unA05+6oAfRNovRrc2oOcDNt/UNa8kOU0jiYIwsckAgtByIBp06BCBQgPV9a3EOMthI9p8fE7nL0bjom+DrNauqGj0h5sfefWecLlKBJ1oaP3MPKY5tEuICYctvVVnlf+Hgp6ZU/FBeEDueazZNP3Vclvbcz98BiazT/F1YcvNdvt8hZhYs91VLCrQHRiNGPW9+TYiqmvCtDRg0Z/QPXByuuDE2H3MGVRSEEQso0ILAQhA/T1Yf16sLCA06eV1bkF4WO4HhrBjL03ABjVoAT5bbRXaFTLasY/+h8/dVWx94eK1CvxxrgJWYYdAyHqMeRygdpjsqvqgpApzrlM2Pi9OyUczHkaFU/rv05z8vZTzXYzfTMW1FlAAxtPfl4TT67Jy9n912tTK0sS1BoN9aYrr88uhM3dlemWBUHIFiKwEIQMKlAAli9Xns+aBVu25Gx9hC9PfFIyA9ddIiFZTe3itrSq6Jgqz4bADVwMu4iuoTE/NJ6G9ObUsVc2gP9WUOlC04WgZ5SqDEH4VNmaGbK2VxWqFLQmKj6Jzkt82X0lRLPdQMeACXVnE1GhKCFWMDFpG3MvzkV+vdtT5V7KqtwqPbi6Cda0hPjIHDgbQfj6iMBCEN5Do0Yw+L877V26wJ07OVsf4csyZ/9NAkIisDbRZ0pT11RBw71lCzm2ajrIMj+W+xEH0zemjn35AHb+N4jbcxjkKZtNNReErGNuqMeyLpWoW9KehGQ1fdZcYPWZe5rturp61J+7hdszehJhIvHX5b8Yd2ocSepXM0pRujm0XQd6JnDnECxvCNFP0ziaIAhZSQQWgvCepkwBd3d4+RJatoT4+HfvIwjv4hsUzoIjykqMk5uUJreZgdb2+KAgImb8Tt+NMXz3ogCtXVprF6BWw9bvIf6lMv3mN4Oyq+qCkOUM9XT4s1052lTKjyzDiC1X+W3/Tc2dCZVKRY9qAxlVZRQqSUXgvg3s6libmOhX4zIoXAs6/QNG1vDoIizxhuf30jmiIAhZQQQWgvCe9PRg3TqwsYHz51/dwRCEDxUVn8Sg9X7IMjQvn4+6pexT5TmUcJUtlWUuFFbRueMsdFTaa1pwdiHcPQp6xtD0L9DRzabaC8LHoaOSmNykFP1rFgZg9v4bjNl+jeTXVulu6dKS2ZWmMGCbmiLnHrNyZDNexr8WXOQrD93+BQtHeHZLCS4eX8vuUxGEr4YILAThAzg6wsqVyvM//1QCDUH4UBN3+BMcHkteSyPGNCyRavvL+JdMufgrGzx0eDmhD0Wsi2hneBII+8cqz7+dADaFUpUhCJ8jSZIY9K0L4xuVRJJgxal79P/7IvFJyZo8NYv5oDfpF84X02NBqVA67+nM4+jHrwrJVUQJLmxLQGQILK0H905leV3j4yEsDG7ehIsXISjInMBAuHsXHj6EJ08gIgLi4sRkVcKXS/ykJQgfqF49GD4cJk+G7t2hbFkoWjSnayV8bg5cD2OtbzCSBDNblsHMUE9ruzo+nhm+vxIeF05Bi4J0d+2hXUBSAmzuAUlxULg2VOiWjbUXhOzR0d0ZaxN9Bq7zY+eVEF7EJrCwQwVMDZTLmHL1OmJSuTJW+7/n1otbtN/dngWVZlAofxmlAPM80GUXrGkNwadhZWNovhSK+WgdJzYWbt+GR4+U7q4vXyrBQMrzNx+vb9PuFqsH1HjrOenoKDMOGhgo/77+MDAAMzNwcEj/YWOjTIQlCJ8SEVgIQiaMGwcnTsCRI9C8OZw5A0ZiEh4hg6ISYfxWZXXtHtULUqWgTao8V/p3p+jD89h46zCu3rjUC+EdnQ4hl8DICr77Q1xpCF+sBq55sDTSp9fKc5y49YzWf51iWZdK5DJVxiO5WLuw0mclvff1psjhOzyd3IaoORMo49FMKcDICjpsQb2+C6pbe1Cvbc8+o9/ZGtSemzfhxg0IDs58PU1NwcxMJjY2HkkyID5eIiEBkpK08yUnK4FMbOyHHUdPD+zt0w888uaFwoWVAEUQsosILAQhE3R14e+/wc0NrlyBH36A//0vp2slfA5kWWbtbRXPohNwsTNjUJ3Ut7sibgeiOn6Osmpobu+Nm62bdoZgXzg2U3neYDaYO6QqQxC+JN8UycXfPavQZakvVx9G0Hz+SVZ2q4yjtbLeS17TvCyvs4SL8+piHhPDutXjWOVvTUJAjf+CB2OC761mgU9/upRdjXdsXw5eecKBEwMAJSi3tFS6u1paKmsXmZsr/775SCvdzEy5E5GYmMSuXXvx8fFBT0+5C6lWQ2KissBqQoJyhyPl+euP+Hjl8fIlhIQoj0ePXj0PCYFnz5SygoPfHQzlywfFi6d+5M4tfocQsp4ILAQhkxwcYM0aqFMHFi8GDw/o2DGnayV86rb4PeLKcxV6OhKzW7lhqKeTKs+i5zvY30WHik/MGNZ4nPbGhBjY0gtkNZRuCSWbpNpfEL5Ervks2dDbnY5LzhL0LIam808y+dtKPPI359gxOH06NyH3d9O2Vg8Ou99Glgfw6NJInh9p8V8JuvTb/yeySW66Fp3DtNpj6dj0CS8rT6Soi+qjdTFSqZQuTgYG7877LgkJEBqqHWy8+XjwQBnz8eCB8ti3T7sMa+u0A478+ZW6CsKHEIGFIGSBWrVg7FgYMwa+/x7Kl4eSJXO6VsKn6kVMAlP3KKtr/1izMCXymKfKc+3ZNVb4r0CdW+KX1tMw0TPRznB8FoTfBvO84PNrdlRbED4JyckQ+ciUBoZVWZ5wlieRkXRbc4qwjRWIf5DSndCWv/ZsonCBCajKbCZfp3EMdj9L1W+nU7SoRJ48EpI0Dk7Zwt7hlIz4E0KfQOU/QdJ/6/E/Bfr6SgCQP//b8z1/DgEBqR9BQRAernTlPXFCex9jY3BxUYIMV1eoVEn5P8089Z8pQUhFBBaCkEVGjIDjx5VfhVq0gLNnlb62gvCmX/cG8jwmEQdjmW7VnFJtjwq4xqxzw1HLauoVqIdHPg/tDM9uw4nflOf1poGR5cevtCDkkPh48PWFY8eUv7EnTijdhMAQycAd22bnMHQMx77NWapRllbf2FO6NOTPr4tKNZY/L+YiacZ8vC/s4FriHew81yFJ/13+uPcF41ywrQ9cWQ8xz6DVStA3eUuNPh9WVlC1qvJ4XUyMMqbkzYDjxg1l28WLymPNGiW/JEGxYkqQkfJwdVUCHEF4nQgsBCGL6OjAqlXK7FABAdC7tzIlrejDKrzuyoOXrDl7H4DmBZLR1dHuc6BOSCCwX0/6PglHam3OsJbDtAuQZdg9DJIToFAtKNYgu6ouCNni5Us4eVIJIo4dU36keXMhUlNTZaHS6tX1qFy1EmvvX+Rg4GNOSedpaF+aAgVSfsqX6Fu2H4dK3UB9cT97da9z5PBApntMx0j3v5k2yrQCY2tY3xFuH4Dl30G7DUraF8rYWBkb6OamnZ6UBHfuvAo0Ll5U2j8o6FXa8uVKXn19Zf/Xg40iRUQ3qq+dCCwEIQvZ2sLatVCjBqxeDZ6e0KPHu/cTvg5qtcyobVeRZfjO1YHCJqlHXd5/cJUH0gtsdaGxz0BsjN6YKSpwF9zaByo9qDddRK7CFyEoCDZtgo0blQvZN9d5yJ0bqld/9ShTRpk8Q6FDzeRyDN9yhfXnHvDz5is8iYynX83CSJKEJEnUHD6Xwx5ruHB3JgnBh+nxbw/+qPkHloaWShFF6kDH7bCmBTw8pyyk124jWKW+o/gl09VVpk0vWhQaNXqVHham3DX6P3v3HV/j9Qdw/HPvzc1eiBixxd57rxo1q6hdNVq0iqITrdWf0damFDVaWhQ1So1Qe+9NjBASImTv5N77++MYjSdthex8369XXnlyz5OT732y7vc533POsWPP3oKCnh0/4eIC1asnTjby50/75yHSjyQWQqSwBg1g4kT44gu1SlSNGtq7QiJ7WnvyLmfuhOBoY8XnLUtyYn/ixMJsMTPeew4n39bR0roG31TqmriD+GjY9oU6rjsE3DzTKHIhUt61a8+SiZMnE7cVK5Y4kShR4t9zaCuDnm86VcTN0YZ5e24wzcsb/9AYvm5f7umoYOP6PVhUojSD/xqM990zbHzvdZpOWUaBAmVUJwVrQL/tsLwjPPSGxc3VyEW+Sql0BTIPd3do00a9gRo49fFJnGicOqVGm3btUm9PFCumbrI1agSNG0Ph7JWrZTuSWAiRCj79VA3hb9mi5lucPCkT37I7NWH7CgDDmpXA3Um7NMz6a+s5EXACO6M9Q9tNQvf8K6kDMyDEF5wLQMNP0iJsIVLU5cvPkomzZ589rterF56dOqk75QUKJL9vnU7HZy1Lk8/FlrGbLrLymC8BYTHM7VEFe+vHG+nlqcrPLX/maP8uVL0Qxul3uxHx62pK5yqtOsldCt7zgl86Q8AFWNoauvykNp8UT+l0KmEoVgy6dVOPxcfDxYuJRzYuXFClVTdvwtKl6rzChRMnGkWLysBrViKVcEKkAr1e1aEWKgTXr6uduS2W9I5KpKdpO7wJioyjZB5Hetctomn3/XUpp+dNRGe2MLjyYAo4PffKKugmHJipjl+fmGUml4qszWJRe/yMHatWyitbFr76SiUVBoNapnvBArU86l9/wYcfvlxS8Xe96hThh7erYWvU89eVB3RbeITA8GeTNDxzeNJ43A8E5LFmURMTfbf35fj94886eLJLd9FGEBcBv3SB0yteLahswGhUo/P9+8OiRep7HBwMf/4Jn38OtWqp7/nt2/Dzz/Duu1C8uPo/+fbb6nOuXZP/lZmdJBZCpJJcueC339Qf2zVr4Pvv0zsikV4u+IXyy9HbAIx/ozzG5yZsxz94QPC30+i5LZoudwvQs0xPbSfbRoIpFoo1hrLtte1CZBAWiyqLGTVKrSRUsSJMmACXLqm/h61bw5IlEBAAO3bAgAGq1CYltSiXl1/71yangzXn7obSaf4hbgZGPG33KF+Tytv2kKNSNSLiIxjoNZBt3pufdWDrouZYVOwKFhNs/BD2fCOvepPJ2RlatYIpU+DIEQgJge3b1c9G3brq5+HuXTUnccAANbfDwwO6d4cffoArV+SSZzaSWAiRimrVgu8ebzEwYoQaIhbZi9lsYczGC5gt0K5SfuoUz6U5Z2/kGX5qZOFMMT1vvT8dg/65zfKubgPvbY8nbH8ndQMiQ7p6Vd2ZLl5c7XswebJavtTGRpU3LV+uJgFv2QJ9+6qbL6mpaqEcrPugLoVz2eMbFEWn+Yc4eTv4aburXQ4WtlhIs0LNcA2Kw67Xp2xZ/OWzDqysocMCaPCx+njPJNg0BEzxqRt4FuboCC1aqHmIBw+qRGPnTvjySzWXxtpajV6tWqX2hKpY0Ui/fq/Tt6+B5ctVm8jYJLEQIpUNHQodO6r6086d1dCwyD7WnbrLKd8QHKwNjG5dRtMeHhfOpONT8KqqJ/DrAZTOXTbxCfExsO3xkrN1BkHukmkQtRAvJj5ezZlo1kyNTnz7rZrUa2cHb70FK1dCYCBs2KDKXVxd0za+om4OrPugLpUKuBAcFU+PRUfYfvH+03Ybgw1TG01l2M0SuIeC7ud1zDw2DcuT2+Q6HTQdA22mg04Pp5fDyu4QG/EPX1Ekh7292mD2669h3z6VaOzerUrnGjcGGxsLwcG2/PKLnnfeUStMVawIH38M27apPTdExiKJhRCpTKeDxYvVJLfbt6FnT7VzrMj6QqPjmbJVTdge2rQEeV1sE7Xr4uKYdXIGgdGBFHEuwsDK72s7OTgLgm+BU35o+FkaRC3Ef/Pzg3HjoEgRlUDs2qXmlrVrpyZmBwaqEtBu3cDJKX1jdXO0YeWA2jQt7U5sgpn3V5zk58O3nrYb9AbaTluDb8daTOlsYPHlZYw+MJr4v49M1HgXuv0KVnZquedlrSE8IO2fTBZnZ6cSinHjVIIRGJjAhAkH+fRTE1Wrqv+n58/D9OmqxCpHDpWYTJmiFkl5fplikfYksRAiDbi6qn+2dnawdasa9hVZ3wwvbx5FxlE8twN96xXVtNtu+JWq49ZSINDC2DpjsTE8t1JU8C04MF0dv/4/sJGt3EX6sVhUAtGpk1rZZ/x48PdX8yNGjVIr/2zapNodMtjaAvbWVizoVY0etQphscCYjReZvPUyZrMamdBbWfH6pGUMf/1rDDoDf9z8g3ELuxMSHvisk1KtoM8WsM8F987C4mbw8Fo6PaPswdYWKlZ8yMSJZk6eVKV0q1ZBv35QsCDExalJ/yNHqv0z8uRRyezixeDrm97RZ0+SWAiRRqpUUX/sQN1d+e239I1HpK5L/mFP74pOaF8ea6vEf24jH/iT68JVSvpDu9xNqJ63uraTbSMhIQaKNoRyHdMgaiG0goNh5kxV6tSsGfz+uxp1bdhQlTrduaNq5jP6/gRWBj0T3yzPp6+XAmDB3psMW32G2IRnQ8gdSnRgbtO5VLpvQ5e5FznYuQW3/C8966RANXjXC3IUVUs/L24OvkfS+qlkW25u0LWr+l96+7aa3D1njhopc3SEhw9h9Wq1EmPhwupndsgQNa8nMjK9o88eJLEQIg117672uAA1efHv67iLrMNisTB2k5qw3aZiPup5umnOWXZvPcP76/nlDRd6dZ+k7cR7h9plW28lE7ZFujh5Ui0J6uEBw4eridhOTjBokCpH2btX3R22tk7vSF+cTqfjwyaeTOtcCSu9jk1n/em95Bih0c/Knup71Oerql9gstLxyBhLrz39ORnwtx38chWH93aCRzWIDoaf3oBLG9Ph2WRvOh2UKgWDB6uRsqAgtX/UmDFQu7Yqzbt6FebOhbZtIWdOlRhPnar215DVplKHJBZCpLHJk9WqGFFRaqWUhw/TOyKR0taf9uP4rWDsrQ182UY7Yftu+F2WX15OsJOOBu+Px8n6uSL0+BjY+ng+Re0PwL10GkQtBMTG6vn5Zx01a6rSkiVLIDpaTZidP1/Nrfj+eyhfPr0jfTWdqhVgad8aONpYceRmEJ1/OIR/SPTT9lLN3yL/yuXs7FOekPgw3tvxHn/c+ONZBw5u0HszlGylloH+rTcc+SEdnol4wmiE+vVVid7hw/DokRpdGzhQzQWKi1OlfJ9+ChUqqFKq995TZcqyqErKkcRCiDRmMKga0eLF1VBuly5qZRWRNYTFxDPpTzVhe8hrJcjnYpeo3RQezpItXxNnjqOYVTGaFGii7eTQHAj2Aad80OjztAhbZHMPHsCoUXreffd13nvPiuPH1UhEz55w4ACcOQPvv5/+E7FTUoMSufltYB3yONvgHRBBh3kHuXwv7Gl73rLVWND+J5oXbk6COYFj337B2tlDnq0YZW0PXVdA9XcBi1q9bftomUGcQbi6QocOaj+MmzdV2dSsWWrSt62tSpIXL1arNbq5Qb16anWq48flW/gqJLEQIh3kyAEbN6qa0N274ZNP0jsikVJmeHnzMCKWYrkdeLe+dsL2xWnj6TBhH28ctdDarjW650ucQnxh/zR13OJ/YJOFXsmJDMffH4YNU3d0p041EBFhTZEiFiZPVnMnVqxQL7iyaiVe2fzO/D6oHiXcHQkIi6XzD4c5eP3ZMLKdlR1TG03lE30reuw1U27eTr5dPpBY0+OdvA1W0GYaNB2rPj48F9b1U3OjRIbxpGxq6FC1E3hQkNqob/hwKFNGJRKHDqkyqpo11STwnj3VDuH37/93/+IZSSyESCflyqkNowBmz4Zly9I1HJECrtwP4+fDT3bYLqeZsG0ym/C+dAArMxSsUJe8hrzaTraNhIRoKFwfyndKi7BFNnT7tporUbSouosbHQ3Vq5sZOfIoly8n8MUXKb8bdkbl4WrH2vfrUqtoTiJiE+i95Bi/n7r7tF2v0/NOzyk86tSQP2obWGE5zLvb3yUoJkidoNNBgxHQYaHaxPLiegwrO2NMkL0uMio7O1WSPH262hH+9m1YuFDtOeXsrEqUf/0VeveGfPmgalW18tSePaqkSvwzSSyESEdvvqk2AgJVZnDsWLqGI16BxWJhzIaLmMwWWpXPS4MSuTXnbPHZwvg2kYx/z4E3e07QdnJ9J1zZDDoDtJYJ2yLl3bih6so9PdWcibg4VZe+fTscPGiiVq37GAz/3U9W42Jv5Od3a9KuUn4SzBZG/HaW77ZfebocrU6vp/7EBTSetBgnayfOBp7lnQ3duX77zLNOKnWFt9eCjTN638M09B4vy9FmEoUKQf/+arPHhw/VZn2jRqmEAuD0abWaY5Mmasf49u3V78/Nm+kbd0YkiYUQ6WzMGPVHKjZW1YPeu5feEYmXsfGMP8duBWFnNPBl27Ka9qj4KGadnAVAi5aDyGWXK/EJCbHw5+MJ27XehzzaPoR4WVeuwDvvqHKQxYshIQFee02VYu7bp+7eZvc81sbKwKyulfmgcXEAvt99gwHLTxARm/D0nJr5a7Gi9QoKOHjQ/rc73Onek6PHNzzrpFhj6LcNi3MBHGMDsFrWAq55pe0TEa/EaIQGDdQSyidPqlKo5ctVaVTu3BARoVahGjRIzZUsUUItabt5s2rL7iSxECKd6fWqjrNMGVXv3KmTSjJE5hEeE8/EPy8DMPg1TzxcE0/YtpjNbJ/1MSFhAXg4evB2mbe1nRyaA0E3wDEPNP4iLcIW2cD582pJ2LJl1YsjkwlatoSDB9UKOY0bS0Lxd3q9js9blmZG10pYW+nZefkBHecdxPdR1NNzirkUY3ntuZS/Z8QtxMzsrWNY6732WSd5ypHQz4tHDiXRxYbDr13U77esb5op5ckDb7+t5hvdv6+SjYkT1T4uVlZw/bpa0rZdOzWa0bQpfPstnDuXPb/lyUosQkNDWbZsGe+++y5NmzalTp06vPHGG4wdO5ZDhw6lVoxCZHnOzmoyt6urWiZv8ODs+Qcps5q18xqB4bEUdXPgvQbaCdu+a5ZT+sc9TFpm4uOqw7E2PLfwf8gd2DdVHTf/Gmyd0yBqkZWdOqXqxStWVBuGWSzwxhuq3HLrVqhbN70jzNg6VCnAbwPr4O6kVoxq//0BDt949LTdrYAnldZvZd8HNTlX2ML4w+OZfmI6Zsvj5YQccnPQ8wvMlXqCxQw7voQNg9RS0iLT0utVedSoUWofl0ePYP16Vcr8ZEnbv/6Czz+HSpXUHjB9+qiVIAMD/6v3rOGFEot79+7Rv39/8uXLx4QJE4iMjKRy5co0bdqUAgUKsHv3bpo3b07ZsmVZvXp1ascsRJZUooTaxVavhx9/VEvkiYzPOyCcpYduATC2XVlsrLQF6psf/EWgM9ysXZBmRVpoO9k+Sk3YLlQXKnZJ5YhFVnbkiNoMrFo19YJHp4O33lLLxW7cCDVqpHeEmUflgq5sGlyfigVcCI6Kp9fioyw/cvtpu33e/AwavIxBlQYBsO7YEpZ+1ZHIOLXFs0VvhanNTGj1rZo3dfZX+KkthAekx9MRqcDZWc2VfDLf4upVtRhLmzZgb69Km3/6SW2O6+4OVaqofTS2b1d7WWVFVi9yUqVKlXjnnXc4duwY5f9hV5zo6Gg2bNjA9OnTuXPnDp/I+plCJFvLlmoDvc8/V8vilSunhltFxmSxWBiz8QIms4UWZfPQuJR2GZ1zgef4wfkU1gOs+LnNt5rlZXU398DlTTJhW7ySEyfUXVSvx+X8er0qgRo9WpVBiZeT18WW3wbW4fN159h4xp+vNlzg6v0wxrYrh9GgR6fT8UHlDyjokB/z+yMp4XeVX4Ja0XbyKtWBTge1BoJbSVjTG+4eh0VNoNsvkL9K+j45kaJ0OihZUr0NGaJKmg8cUEnE9u2qNOrMGfU2daraJ6ZuXbUbeLNm6maA1Qu9Ks/YXmjE4uLFi0ydOvUfkwoAOzs7unfvztGjR+ndu3eKBfi8efPmUbRoUWxtbalWrRr79+//1/P37t1LtWrVsLW1pVixYvwgt4FFBvfpp+oFQUKCutPo65veEYl/8se5exy5GYSNlZ6vkpiwbbFY+Pb4twC0Kt2ecvkqJ2rXmRMw7Hg8n6Jmf8ibybczFmnOxwd69FAjEV5e6oVJ375qsvYvv0hSkRJsjQZmdq3M5y1Lo9PBiiO+9Fp8lKDIZ+uOti3RnsLd+hFmr2OtZxDv7HgH/wT/Z50UbwL9d6sEI8wPlrSCC+vS4dmItGJj82y+xdmzEBCgqhLefVetQhUXp5av/fJLqF1bbdLXoYPa2f7q1cxbDv1CiUXu3NplE1Py/Be1evVqhg0bxujRozl9+jQNGjSgVatW+P7DKy8fHx9at25NgwYNOH36NKNGjWLo0KGsWye/zCLj0unUqi2VK6uazA4dsu6QaWYWEZvAxC2XABjcxJOCOe015xyeOByOnsbOyo6hVYdq2osHbkP36Do4uEPjkakes8g6goLg44+hdGn1YgWgVy/w9oYlS1RppUg5Op2ODxoXZ1Gv6jhYGzhyM4j23x/g6v3wp+dU6v8J+basx6ZoUQKiAlgYsZA/Lq551kmu4vDeTijRQpU+ru0Hu76WbZ6zCXd3ddPwxx/h1i24dk2VUHXqpDbNDQ2FDRvUHMvSpVXy0bevukGQmTbpS/aqUD/99BNbtmx5+vFnn32Gq6srdevW5fbt2//yma9u+vTpvPvuu7z33nuUKVOGmTNnUrBgQebPn5/k+T/88AOFChVi5syZlClThvfee49+/foxderUVI1TiFdlb6/+wLi5qUmY/ftn3rsXWdWcXdcICIulcC57+jcspmkPPXuKHCu2M3q1mcGuHXC3f65MKsyfUvc3quPmE8DONfWDFplebCxMm6b2oZg+Xd31bNpU/Z34+We14Z1IPc3K5mH9h/UolNOeO0HRdJx3EK9Lz+ZMFMpXihWtV1A/f33yBsbj0fdrfvq2N3Gmx6Mbti7QfRXUfXyjYf9U+K0XxMo6pdmJTqd+h99/H9auVTcRjx9XpdBNm6rRjrt31ca5b7+tNumrUAEiI9M78v+W7GquSZMmPX0hf/jwYebOncvMmTPZvHkzw4cP5/fff0/xIAHi4uI4efIkX3yReBnGFi1a/OOKVIcPH6ZFi8QTJV9//XUWL15MfHw8RqNR8zmxsbHE/m2tz7CwMADi4+OJj49/1aeRbE++Znp87awms13L/Plh5UodLVsa+PVXHZUqmRg+PP3vbGW265gafB5GsviADwBfti6FATPx8Ym/N7+F7SWkhg43kx1vvTZYc710O8diZY7F5FEDc9lOkI2v56vKDj+TZjOsXq1j7FgDt26peTjlylmYMsVEixYWdLpX/xHKDtcxJRTNacvagTUZuuosR3yCGbD8BCOaejKwYVF0Oh32enu+q/sdf67ohHO0L3a7jvNOqV582+g78jnkU500GYPOrTSGLcPRXdmMZXFzEjovB9fC6fvkMpjs9DNZqZJ6+/hjiI6GQ4d07Nql46+/dJw+rcNkAmvrhJf6PX/V65icz9NZLMm7D2pvb8+VK1coVKgQn3/+Offu3ePnn3/m4sWLNG7cmMBUWk/L398fDw8PDh48SN2/rZM3adIkfvrpJ65evar5nJIlS9KnTx9GjRr19LFDhw5Rr149/P39yZcvn+Zzxo0bx/jx4zWP//rrr9jba0sdhEhtW7YUZdGiiuj1Fr766jBVqmSTNesysKVX9ZwJ0lPW1czAMtpkL9wczoywGcQRR2e7t6hkUzlRu0uUD42vqi3X95SaQKh9kTSIWmRW58+7sWxZOW7ccAUgZ85oevS4QpMmvtlyl+yMwmSG9bf07A9QxR9Vc5npXtyM9ZPvidlM/L4NzC95kQf2sdjr7Ols35kSxmd1ajkib1Dz5kxsE0KJNThyvOhQHjmVTodnIzKysDAjDx/aUaxYWLp8/aioKHr06EFoaCjOzv++HHqyRywcHR159OgRhQoVYseOHQwfPhwAW1tboqOjXy7iZHh+RRWLxaJ57L/OT+rxJ0aOHMmIESOefhwWFkbBggVp0aLFf17M1BAfH4+XlxfNmzdPcoRFvLjMei1btYL4eDPLlumZPbsOhw4lULx4+sWTWa9jSjlzJ4Qzh4+h18F3b9ejZB6nRO0Wi4XxR8cTFxZHhVwV+KLFSM3fG8OvnQC4k6MuNdv3z5bXMSVl1Z/JS5dg1CgDf/6pXrg6OVn45BMzH31khb19eSBlJ/tn1euYmtoBK4/fYcLmK5x6pCfOxpX5PSuTy86Al5cXrSfOp0ZsIJ8e+JTLQZe5t38pHtXb07HrWPS6x9XoYZ0wr+mFzf2z1Lv5LebXp2Cu2ic9n1aGIT+TKeNVr+OT6p0XkezEonnz5rz33ntUqVIFb29v2rRpA6iVo4oUKZLc7l6Ym5sbBoOB+8/NYHnw4AF58uRJ8nPy5s2b5PlWVlbkypUryc+xsbHBxsZG87jRaEzXH+r0/vpZSWa8lj/8oFZ5OXJER6dORg4eVJvppafMeB1flcVi4Tuv6wB0qlqAcgVyas659P0UCu5eT85Gej5v/TnW1s9thnd9F/jsxWKw5nK+TjTJhtcxtWSVn8l792DsWLWIg9kMBgMMHAhjx+pwdzcAqTtMkVWuY1p5p24xSuZ14YMVJ7ngH0bHH44yr3slQF3LwvaFWd56OQt/+ZjXduyCHeuZbPJjePfZuNi4QK7C8O522PghugvrMGz9BMPDq9ByMhjk+wDyM5lSXvY6Judzkj15+/vvv6dOnToEBgaybt26py/QT548Sffu3ZPb3QuztramWrVqeD1ZpPsxLy+vRKVRf1enTh3N+Tt27KB69eryAyoyFRsbWLdOzbu4dAnat4cY2cA1ze2++oBjPmp52eHNS2raTZGRxP64gkYXLLwdXoFKuSslPsFshp2qBMpcrS/RNqmzgp7InCIiVELh6QmLFqkflw4d4OJFtQSlu3abFJFB1C6Wi02D61MqjxOB4bH0XHKCwwG6p1USNgYbPuwylbCm1ThY3sA6TtJtczeuBF1RHRjtoNNiaDoG0MHxRbC8A4RnouWAhCAZicXChQu5f/8+rq6uzJ07l40bN9KyZcun7ePHj2f06NGpEuQTI0aM4Mcff2TJkiVcvnyZ4cOH4+vry/vvvw+oMqZ33nnn6fnvv/8+t2/fZsSIEVy+fJklS5awePFi2bxPZEr588Off6qdPvftUytFmEzpHVX2YTJb+GarmsvVp14R8rvaac7Z/fAw47vA7ipWtPnwO20nF9bC/fNg44y53ghtu8iWTCa1BKWnJ0yYoJaXrl0b9u+H33+HUqXSO0LxIgrmtGfdoLo0L5uHuAQzq24aGP7becJi1MRXva0ttecsp/7clXg4FeBuxF16/9GTP/f+qDrQ6aDBx9DtV7B2hFv7YX49uLYzHZ+VEMnzwonFypUrKVKkCLVq1WLSpElcunQpNeNKUteuXZk5cyYTJkygcuXK7Nu3jz///JPChdUqCvfu3Uu0p0XRokX5888/2bNnD5UrV+brr79m9uzZdOrUKc1jFyIlVKqklqG1tlYjGB99JMvQppX1p/24GhCOs60Vgxp5atrjTHFMOzGNG/l1mD8bSH6XAolPSIiFv75Wx/U+AvukyzFF9nL0qEoi+vdXG2gVLw5r1sChQ1C/fnpHJ5LL0caKBW9X47PXS6DXWdhy4T5tZx/g7J0QQM3vLJunAqvbrqa+R3267ogm3+BpLJ7T/9mStKVbq8308lSAqIfwSyfY8RUkxP3zFxYig3jhxGL37t3cu3ePIUOGcObMGerUqUPx4sUZMWIEe/bswZxGG7wMGjSIW7duERsby8mTJ2nYsOHTtmXLlrFnz55E5zdq1IhTp04RGxuLj4/P09ENITKrJk1g+XJ1c+v779W61yJ1xcSbmL5DjVZ82MQTF3ttKeXKU0u5G3GX3Ha56Ve+n7aT44shxBcc80LtQakdssjgHjxQO/DWrg0nTqiRyOnTVanjW2+p32+ROen1OvrXL8pH5UwUcLXFNyiKTvMPsXDfDcxmdSfIxcaFuQ1mUDu2ALbxsC/gEL239uZexD3VSe6SajO9Gv3Vx4dmw9KWEOSTTs9KiBeTrDkWOXLk4O233+a3334jMDCQ77//npiYGHr16kXu3Ll55513WLt2LZGZYQcPITKxLl1g1ix1PHo0LF2avvFkdT8fvoV/aAz5XWzpXbeIpt1/15+UGTCLpqfNfFT1I+yNzy1NHRMK+x6XRjUZCdaydHV2lZAAc+ZAyZJqh2yAPn3UjtnDh6vRSJE1FHGCjYPq0KZCPhLMFib9eYW+y47zMELtlWWwsaXOqj8J+2Y418u5cuHRBbps7sIhv4OqA6MttJkKXVeArSv4nYQFDeHCuvR7UkL8h2RP3n7C2tqali1bMm/ePO7cucP27dspUqQIX3/9NdOnT0/JGIUQSRgyBJ7sF9m/P2zZkr7xZFWhUfF8v/sGAMObl8TWqF2R58LSmThFW6gYlZN2xdtpOzk4C6KDwK0kVH47tUMWGdS+fVC1KgwdCqGh6vjQIXVj4B8WNxSZnLOdkbk9qjCpQwVsrPTs9Q6k1az9HLz+EACdlRW12g9gddvVlMlZhtjQYO716c+q38ZitjyuBCnTDt4/AAVrQ2wYrO0Hm4ZCXFQ6PjMhkvbSicXzqlevzoQJEzh79qxmd2whROqYNAneeUdN/uzcWdVri5Q1b+91QqPjKZXHiY5VC2javYO9+bzZfRa9rqfSZxOfrU3/RNg9ODxPHTcdC4Zkr/ItMjk/P+jRAxo1gvPnIWdOtYT0sWNQp056RydSm06no0etQmwaXJ8S7o4Ehsfy9uKjTN1+lQSTSh4KOBVgeevljLpQjLJ3LLjP+I2PvD7kYbRKQHAtCH22QINPAB2c+gkWNYGAtJ/vKsS/SfZ/OIvFwtq1a9m9ezcPHjxINLdCp9Oxbt06WcpViDSi06nVZB48gG3boE0bOHhQVpFJKf4h0Sw9eAuAz1uVwqDXbrj53fHvSNBZoMPrVPNsqO1k7xRIiIaCtaB0mzSIWmQUcXEwc6Za6SkyUv2+vv8+fP01/MNWSiILK5XXiU2D6zNh80VWHrvD3N3XOXLzEbO6V8HD1Q4bgw1vTFnJ0YT3mFfkMlfvHeDMxg58VfsrWhRpoW5KNP0KijaA3wdA4BWVXLScDNX6ysQckSEke8Tio48+olevXvj4+ODo6IiLi8vTt/TYmVqI7M5oVKvI1KgBjx7B66+Dv396R5U1zPDyJi7BTK2iOWlSSruJwMH9Kznifxij3sjwasO1HQR6w6nl6rjZePnHn43s2AEVK8Lnn6ukok4dNUl73jxJKrIzO2sDkztWZG6PKjjZWHHidjCtZu5j2wW1X4XewYE681cysf9qSuYoSUhsCL/+OJwF33QnJCZEdVKsMbx/EDybQUIMbB4Oa/pAdEg6PSshnkn2iMWKFSv4/fffad26dWrEI4R4CY6Oao5F3bpw/Tq0bg1794KLS3pHlnldvR/OulN3AfiiVWl0zyUFUb4+uHzwNRPywt1xXSnoVFDbya7xYDFBqdZQWGpesoNbt2DECFi/Xn2cJw98+63ad0afYsXHIrNrWzE/lQq4Mnjlac7eCeH9FSd5p05hRrUug63RQKmcpVjVZhU/7p9OlVnLcIk6w5TQlrQe9C0NCzQEx9zQYw0cnqv+zlzaAP6noNMSKFgjvZ+eyMaS/WfOxcWFYsWKpUYsQohXkDs3bN+uXsicPat27I2NTe+oMq9vt13BbIFW5fNSpVAOTftfOxeToAeLjZE+NZNYPtb3KFzZDDq9mlshsrToaFXyVKaMSioMBrXK09Wrah6UJBXieQVz2rNmYB0GNlSvqX4+fJs3vz/I9QcRABgNRt6v/zGOPbtx18OG7cUj+HDXh4w9NJaIuAj1Q1VvKPTbAa6F1XLWS1vCgRlq23Yh0kGy/9SNGzeO8ePHEx0dnRrxCCFeQbFisHUrODnB7t3qBY38f0m+ozcfsevKAwx6HZ++rp2wEhobymS73Xw00IDh88E42TglPsFigZ2Pk4nKPcG9dBpELdLLli1QrhyMHQsxMWqvmbNn1b4UMmoo/o21lZ6RrcvwU7+a5HKw5sr9cNrNOcBvJ+5gsVjQWVlR/uOx1N9ygO4V30GHjt+91zFjZHOOXvtLdVKgGry/H8p1BHMC7BwHKzpCxIN0fW4ie0p2YtG5c2eCg4Nxd3enQoUKVK1aNdGbECJ9VakCv/+u5l789pu6ayq7c784i8XC5K1XAOhWoyDFcjtqzll6YSlhcWHkKliCtg3e1XZydSv4HgYrW2gyKrVDFunk7l3o1AnatgUfHyhQAFavhl27VKIhxItqVDI3Wz9qQD3PXETHm/hs7TmGrjrDo8d7XtjZOvJZjc9Y/Ppi3rjhyltbQoju9SHf7P8f0QnRYOsCby2BdrPByg5u7ob59eDKn+n8zER2k+w5Fn369OHkyZO8/fbb5MmTR1N3LIRIf82awU8/qSUuZ88GDw/47LP0jipz2HbhPmfuhGBnNPBRsxKa9vtnj+B1cDm4wEdVP8Kgf25fC1OCqnkGqP0BOOdPg6hFWkpIUL9XY8aoidlWViqBHzNGzXcS4mW4O9vyc79a/LD3BtO9vPnjrD/7rwUyqnUZOlcrgE6no0beGhRvP5Xr+4byV6lI1t9czf6HR/hfvf9R2b0yVOsNBWvCmr4QeBlWdYfSbaHVt+Dikd5PUWQDyU4stmzZwvbt26lfv35qxCOESCHdu8O9e/Dxx2plmrx5VWmU+GfxJjPfbb8KQP8GRXF3sk3UbrFYuDHyU77xiWLT20VpVKCRtpOzv6plIO1yQL1haRC1SEuHD6slY8+dUx/Xqwfz50OFCukbl8gaDHodHzbxpJ6nGyN/P8/le2F8tvYca0/eZVKH8ni6O5Gzem2qb9tLfOBxDh4dz+2w2wxb8w69c7SiZ9evsXYvAwN2w95v4NAcNdfr5h547Suo2R+evxkiRApKdilUwYIFZVlZITKJESNUYgHw7rtqrwvxz1Yfv8PNh5HkcrCmf0PtIhV373tzWxdEvBW0eHO4dsQ2Lgp2T1bHDT4BO9fUD1qkiaAgGDBArbx27pza5G7xYrWbtiQVIqVVLujKpsH1GNW6NHZGA8d8gmg1az/Td1wlJt6E3s6OeoUasr79etoVbcvAzQnUnLCJaV+24NKjS2C0g2bjYOA+KFAT4iJg2+ew6DXwP5PeT09kYclOLKZNm8Znn33GrVu3UiEcIURK+/ZbVRKVkABvvQXHj6d3RBlTZGwCM3deA2DIa5442Wo3+vzhxs9M7qJn+Zc1qV6uubaTYwsg3B9cCqk7gyLTs1hUWWGpUrBokXqsXz+12lO/frLak0g9RoOeAQ2Ls2N4Q5qUyk28ycLsv67TatZ+Dl1XO3I7Wzvzv1rjKFmiFglWsCf3Q3pu6cn8s/OJN8dDnnLQbzu0nQE2LnDvjNpUb9soiI1I3ycosqRk/0l8++232b17N8WLF8fJyYmcOXMmehNCZCx6PSxdquZdREaq3bm9vdM7qoxn8QEfHkbEUiinPT1qFda03wi5weabmwHo1/RTbQdRQbB/hjp+bTRY2aRmuCINXLoEjRtDnz7w8KGakL1/vxqpcHNL7+hEdlEwpz1L+tRgXs+quDvZ4PMwkh4/HmXEb2pyt97Ghmqzl5J/0zrKVW1BgiWBeWfm8enCjlwKOKf+CVTvB4OPQ/lOYDHDke/h+1oyuVukuGTPsZg5c2YqhCGESE3W1mqlqMaN4dQpaNgQdu6E8uXTO7KM4VFELAv23gDgk9dLYW2V+J6LJSGBXTM/w6qAiYbFm1PeLYkLt38axIZCngpQoUtahC1SSVQUfP01TJ2qRvrs7dVSssOHq9XWhEhrOp2O1hXyUb+EG1O3X2X5kdv8fsqPv648eDq5O3exskwrOo0/ff5k4dYJ9P7hOv4/d2Xd6NYMaPwZeZzyqJWjKvWALSMg5LZM7hYpLtmJRe/evVMjDiFEKnNyUntctGih1thv3FhtqFetWnpHlv7m/HWdyDgTFTxcaFshn6b90op5NFh1iULu4LnxQ20HIb5wbKE6bjZO6mMysc2bYcgQtYM2wBtvqBWgCmsHsYRIc862Ria0L0+HKh6M/P08V+6HayZ3tynWhkql4YHtKEIc4/gtcDt/bNhP33J96V2uN/YlmsGgI7DvW5ncLVLcC/33i4yMTFanyT1fCJE23N3hr7+gZk149Aheew0OHkzvqNLX7UeR/HL0NgBftCqNXq9dQntL4B4euMDDxhXwzOGp7WT3JDDFQZEG4Nk0tUMWqeDOHejYEdq1U0lFwYKwYQNs3ChJhch4qhTKwR9D6v/j5O4CTdtQ6a8DlJw6h8ruVYhOiGbBqe9Z+GEjNh9fgdloK5O7Rap4ocTC09OTSZMm4e/v/4/nWCwWvLy8aNWqFbNnz06xAIUQKStnTvDyUuVQYWFqBGPXrvSOKv1M2+FNvMlCgxJu1PPUFs4fu3eM5e7X+PgDGxp9NEXbwf3zcHaVOm4+HmRvn0wlPl6VPJUpA+vXqz0pPv1Uza9o3z69oxPin/3X5G6DkxMVKzbj51Y/812j7+hy0ZnX90VgP3Qi3Td15fj94zK5W6S4FyqF2rNnD19++SXjx4+ncuXKVK9enfz582Nra0twcDCXLl3i8OHDGI1GRo4cyYABA1I7biHEK3B2VmVRHTrAjh1qQve6dep9dnL+biibzqobJl+0Kq1pt1gszDo9C4AOpTtTMJd2CVp2jgcsUK4DeEhdWWZy8KDak+LCBfWx7EkhMqMnk7u3XrjPuE0Xn07u7ljFg89blSaPsy0ti7SkTo+ceF/9nO2lQ7kUcoV+2/vRtFBThlUdRpHq/aBUG9g+Ei6sU5O7L22ElpOhTDu5YSJe2AuNWJQqVYo1a9Zw48YNunXrhr+/P2vXrmXRokXs2bMHDw8PFi1axK1bt/jggw8wGKQ+T4iMzt4eNm1Sd2VjY+HNN2HNmvSOKm19s+0KAG9Wzk+5/C6a9qPLvkV39Ay2ehsGVEzihonPPrjuBXorVZ8sMoWHD9VSsfXrq6QiVy748UfZk0JkXk8md+/8uBHv1CmMTge/n/aj4be7Gf/HRR6ExeBSrSbVN+3i03Hb6FqqK3qdnjuHdnK2Y2sWrvyEUGtbNbm75zpwLQxhd+G3XrCgoVo9ymJJ76cpMoFkTd4uUKAAw4cPZ/jw4akVjxAiDdnYqGSid29YuRK6dYPo6OyxQ/c+70AOXH+ItUHPxy1KadrjQ0Ownv0zo6PNnPy0Ibntcyc+wWIBrzHquFpfyFU8DaIWr8JshiVL1E70QUHqsffegylTVHIhRGb398ndE7dc5sTtYJYevMWvR33pUasQHzQqjruzO1/W/pJupbpxs3cvCvqFcGfDn7TRHeGDSh/QpVQXjIOOwIHpcHge3D+nVo/KVwkaj4SSLWUEQ/wjWbpEiGzOaITly9XO3GazSjLmz0/vqFKX2WxhylY1WvF27cIUzGmvOWfnLS92lbdwK5+Btt2/1HZyaQP4nwZrR2j0eSpHLF7V2bNqhKJ/f5VUVKyoSqEWLZKkQmQ9VQrlYM37dVjxbi2qFc5BbIKZpQdv0eDb3Uz44xIPwmLwzOFJk0UbiWnTkKPtihMaG8qUY1Posbo9e27uxdJkNAw7D/WHg9EB7p2Fld1gYSO4ulVGMESSJLEQQmAwwMKFMHSo+njQIJg2LX1jSk2bzvpz6V4YTjZWDH5Nu8pTvDmeOTeW8nMzA3dmDMbV/rnNP03xsGuCOq47BBxza/oQGUN4OIwYoZZVPnwYHB3Vz/bJk1C3bnpHJ0Tq0el01C/hxtrnEowlB32eJhjBds5UmbaApT3WM6bOGHLa5qTuH7ew6TmCydM6cjHmvlo9KskEozFc3SYJhkhEEgshBKC2Xpg5E0aOVB9/8gmMH5/1/mfEm8zM2Km2Hh/YqBg5Haw152y4voE74XfIaZuTt8slURd25hcIugkOuaHO4NQOWbwEi0WV+ZUuDTNmgMkEb70Fly+rRMMq2bs4CZE5/T3BWP5uTaoWck2UYHy9+RJBkQl0LtmZzW3WU/++C66RcC7Sm26bu9F3W192PTyD6bWvYNg5qDfscYJxBlZ2lQRDJCJ/WoUQT+l0MGmSuqs7ejSMGweRkfDNN1mnpHb9KT9uP4oil4M1fesV1bRH3LlF6PgpuNWy8F7NAdgbnyuTSoiFfVPVcYOPwcYxDaIWyXH9OgwerDaABChWDL7/Hlq2TN+4hEhPOp2OBiVyU9/TjQPXHzLDy5tTviEsPuDDiiO3ebt2YQY2Kkb1bXu5vX09RVxPc8VnGycCTuCy7RgXox1x69mLdo0+wanuELW53rFFzxKM/FXUHIwSLbLOPwyRbDJiIYTQGDVK3eUF+O479SLNbE7fmFJCXIKZWbuuAfB+o+I42GjvrZz85gvqnYxi6HYrOpfsrO3k1M8Qegec8kG1PqkcsUiOmBiYMAHKl1dJhbU1jBmjVn6SpEII5UmCse6DuvzcryZVHo9gLD7gQ8NvdzNxx3XsG7dnSoMpbOu0jffK9OWtw9B8bxhHNsyn6ZqmTLqwkFs1+yYewfA/Db92UftgeG+XEYxsKtmJRZEiRZgwYQK+vr6pEY8QIoMYNkzNu9DpYN48tTxnQkJ6R/Vq1py8g19INLmdbHi7tnY75Yi4CBYXvsW5IjrsBvTB2vBcmVR8DOx/PPmkwcdgtEuDqMWLOHMmN1WrWjF2rFo+uVkzOH9elfPZybdJCA2dTkfDkrn5/W8JRky8mR8fJxj/23wJvdmVodU+ovSE7wirVZp7dT2JTohm5ZWVfDqnLTPmDORQyaZYPjoL9T4Co/3fEozXVIKRFe5KiReW7MTi448/ZuPGjRQrVozmzZuzatUqYmNjUyM2IUQ6699frRhlMMBPP0GPHhAXl95RvZyYeBNz/7oOwKDGxbGz1u638/OlnzntHsmKgcVp1i6JuRMnl0L4PXAuAFWzwZq8mcDdu9Czp4Fx4+py/bqOfPlg1Sq18WPJkukdnRAZ398TjJ/61aRywWcJRt3Jf9F/xSmO5a9C5cVr+a3TBhY2X0ijAo3ost9My2WX2PG/D+iwsz+/FSpP9ODjf0swTqkEY3Zl2D0JHt1I76cq0kCyE4shQ4Zw8uRJTp48SdmyZRk6dCj58uVj8ODBnDp1KjViFEKko5491SRYo1G979LFQFxc5quiXH38DvdCY8jrbEv3moU07cExwfx08ScABlcZjJX+uTKpuCjYP10dN/wErGxSO2TxL6Kj4X//g1KlYM0aPXq9hcGDTVy+DF27Som3EMml0+loVDI36wepBKNa4RwkmC3svPyAQb+coubEXXy54QI2CaWZ3XgWVVq8TXQOe45WsedG6A2+PvI1XVd2ZlGUhfv9d0LdoWDtBCG3Ye83MKcqLH4dTiyF6JD0froilbz0q4NKlSoxa9Ys/Pz8GDt2LD/++CM1atSgUqVKLFmyBIvU1gmRZXTooHbptrWFP//UM2FCbQID0zuqFxcTb+L73Wq04sPXPLE1akcrjg3rS6PDEZR3LkXzws21nRz/ESIfqB1pq7yd2iGLf2CxwLp1ULYsfPUVREVB3bpmpk7dy/TpZly0G6gLIZLhSYKx7oO67BzRkEGNi5PPxZbQ6Hh+OepLx3mHaDpjP1srdyb3H3v47b2/+KzGZ3g4etB0byj1P1/LotFd+dg6itO912DpsAiKNwWdHu4cgc3DYGpJWNNHlUqZMnmNrUjkpVeFio+PZ/369SxduhQvLy9q167Nu+++i7+/P6NHj2bnzp38+uuvKRmrECIdtWwJ27ZB27YWLlzITe3aFtasgVq10juy/7biyG0ehMfi4WpHl+oFNO13j+2h0J6r9NZBaM+u6HXP3XOJjYCDM9Vxo8/AYEz9oIXG+fPw0Uewe7f62MNDLS7QqZOJrVtD0zc4IbIgT3cnPmtZmo9blOLIzUesO3mXrRfu4/Mwkmle3kzz8qZ2sZx0rNqYVa06c2P3QMy6Y5wvBJdv72DH7R2UMrvTxKYClbotpWagD9bnfoMHl+DievXmkBsqdIFK3SBfxfR+yuIVJTuxOHXqFEuXLmXlypUYDAZ69erFjBkzKF269NNzWrRoQcOGDVM0UCFE+mvUCPbtS6Bt21ju3HGkQQO198UHH2Tc0pOouAR+2Ktqe4e85omNlXa0YknsboJb6qkQl4e+td/SdnJsAUQ9gpzFoGK31A5ZPOfRIxg7Vu0IbzaDjQ189hl8/jk4OEB8fHpHKETWZtDrqOfpRj1PN75+M4FtF+6z7tRdDt98xJGbQRy5GcQYo56W9YfxVncj40tZsfLqr2z12UqpI/d5bbc/B8vsYMRbjtQtU5fGNXvQIOAmuS5ugshAOPK9estTXiUYFTqDU970ftriJSQ7sahRowbNmzdn/vz5vPnmmxiN2jt3ZcuWpVs3+ecrRFZUvjxMnbqXNWtasX69ng8/hEOHYMEC9SIvo/n58G0eRsRRKKc9nappRyt8w3z53Wcjpip6erWciu75DCkmDA7OVseNvgCDbP+TVhIS1M/VmDEQFKQe69QJpk6FIkXSNTQhsi0HGys6VStAp2oF8AuJZsNpP9adusvNwEg2nPFnwxnIs9eGN6t0Z3GTocT6TiHedjt+xRyITohkl+8u9sXvZNhGMw8rFselcQcaPrqN57U96AIuwI4vwWsMFG+KrnxnDOYMetdKJCnZ/yFv3rxJ4cLaZRr/zsHBgaVLl750UEKIjM3ePoFVq0zMnavns8/gl1/gzBn4/feMtRJPRGwCCx6PVgxtWgKjIXGJk8ViYe7pOZgsJhp4NKBqnqraTo7+ADEh4FYSKiQxmiFSxe7dquzp/Hn1cfnyMGsWvPZa+sYlhHjGw9WOD5t4Mqhxcc7eDWXdybtsOutPQFgsC/beZMHem+RxbknNEV2o5uHIxPzh+Eaf4L7XH9S4dpuHAXcYVMKfmTodHmUq0yI2F7Wj/ahx9xzG615YXfeitc4ADxdC4dpQqA4UrA0OudL7qYt/kOzEokmTJhw/fpxcuRJ/U0NCQqhatSo3b95MseCEEBmXTgcjRkCNGtClC1y8CNWrw9Kl6q5yRrDsoA/BUfEUc3Pgzcr5Ne1XN/9CnZmbudXYwJC2Q7QdRAfDobnquPEXoNeWUYmUdesWfPKJmqANkDMnfP01DBgAVjJYJESGpNPpqFzQlcoFXfmybRl2Xwlk3am77Ln6gICwWP64FMgfl9SKHw7WxWnsOoSLbQ9jtg+ingecCDiGX+R9yi+6iyUG3unqSb7CeWgUeIdaQX7k8TsOfsfVbt+gbvQUepxoFKoNOYpm3Hrcl2SJj0eXRFVQRpfsP9O3bt3CZDJpHo+NjcXPzy9FghJCZB4NGsCpU2qJz/374a234OOPYfJktURtegmLiWfhPnWj46NmJbAyaBfBuzdvLqX9oOPDIpTJVUbbyeF5EBsK7mWhbIfUDjlbi4yEKVPUZOzYWNDr1dyd8eMhl9ycFCLTsLEy0LJ8XlqWz0tMvImzd0I4cTuYE7eCOHE7mPCYBLY8gC1WdSAODLt1lMnfCU9nb/KEf48hzoSPUywXou/g5Qj1buejnL+egNL2WOWNxTPsIcUjbuN59jpup35GB+CYRyUYBWur93krZpiyVYvFQlBkHDZGA4422pgscXFgMKAzqBtXoRs3EjB1Ko71G5B/8iR1UkKsmufnrL1BltG88FXftGnT0+Pt27fj8rc1/UwmE7t27aKIFL0KkS3lywe7dsGoUar+fdo0OHYMVq9Wbelh8X4fwmISKOHuSNuK2j/GZx6cYWybCN48YqDDx5O1HUQFwZH56rjxSPVKV6Q4i0VtaPfZZ2qzO4AmTVTZU4UK6RubEOLV2BoN1CqWi1rF1N0Bs9mC94Nwjt96nGjcCsYvJJoLd2O4QCG2tJhIsdC7GKIdKOZ0nQjDOapdv0H9Swn84hjBuoJ6yJUD21gLn/xu5kEuHSfrJ1AsIZbid3fheXMbxePiyWWwQ1eg+uPSqRpqmXCnvGDjlCrPMzrOxN3gKHyDorgTFIVvUDR3gtXxnaAoIuPi+aZTBTqXc0dvb//0826/05uo06cpunIltoVyQvAtdA9OYQp8SOxRL1hyWu0DEuavFg8ZmvH3i3vhxOLNN98E1HBX7969E7UZjUaKFCnCtGnTUjQ4IUTmYTSqu8116kCfPmr0ompVlVyk9SJxIVFxLDngA8CwZiUx6BMPkVssFmadmkWwk47QQR0pWiiJV7CHZkNcOOStAKXbpkXY2c5ff6lk9OhR9XHhwiop7dgxy1U1CCEAvV5H6bzOlM7rTK/aar6uX0j00yTj+K0grlpZYQkAv4DcQB12Op8joNQlTtu5YRWmw9ruAUUe+lLxViBBDy0sbGHNSawB6PmXiVsBsLu6hZjoy3heOEfRk3NxNFuww4ydwRZbu5zY2+fC1sEdO8d82Drlx87ZA1uXQuic86sE5LkNUE1mC/dCo7kTFM3tR+HcePQAn+AH+IU94n74IyISwtAZosAQRcX7/uSLCONaISse5IpD5xRFnTuReH5gxLdoYYqM76uSheBbEHAB4uOJmfY6toXDAXCI01GkuRU2zvfA1/tZEFGP1J2YDP7H8YUTC7PZDEDRokU5fvw4bm5uqRaUECLz6thRTbTt1AkuXFCTbb/5Rs3HSKu/h4v23yQ8NoHSeZ1oVV67ZOHhO/s5EXACo97I+xXf13YQEQhHF6jjJqNltCKFHTkCo0erxALA3h5GjlQldHZ26RubECJtebja4VHZg/aVPQAIjY7ntG8wJ24Fc8znEVesK3AifyVMZgs8rriPiQ1nRpULGPUhRPvlRW8TgN4mgLK3L1PifgI7K+s5aWfLSTtbyt02M/ZXM7fcYdC7VkA8cJ/+v/tROOAUqxvqOV9U/Y0vGGTijaMWwh1hdy0rDBYDOouRCpfiyf3IxL7ycO3xKHypOxbGrzXxyBk+e/fZy+nOXiYq3rIwu52eR/lVv6EOFuwjoom9egnL6l5P/xfmLWuFvqIFK3sT6Azg4oEhRxHsXAtDjiLP3lwLg4Nbhk8q4CXmWPj4+KRGHEKILKRkSfXiceBAtWLUJ5/A4cOwZAk4O6fu1w6KjGPpwVsADG9eEv1zoxXm2FjMPYfybgET5v6dyeeYRK3WwZkQHwX5q0LJlqkbcDZy7hx8+SX88Yf62Npa/YyMGgV5Zcl6IQTgYmekcSl3GpdyJz4+nj///JPXW7YgLNZMQFgsAWExBITHEBBahYCwWOqHx3A/NIYHwbHMKXWDovnucNqSi2i/SPQ2ARhCbwI+JGCDISYXVroY0MdR6EEkJf3BLu7Z13aM0NPojAm/nPBzAwATYKLnVZUseOfTcy2fShas9GacYgCDhQZR0biazLiaTbjmtCLMrKNbXAx978XhYjLjmmDGvoUeh7wu6HJXU4lCjiLY5Cj8LHFwKZAlNl99ocRi9uzZDBgwAFtbW2bPnv2v5w4dOjRFAhNCZG4ODrB8OdSrp5YNXbdOLR26bp0a0UgtC/beICrORHkPZ1qUzaNpP7ZxIbkCY6kVpcOzcj9tB+H34fiP6rjJ6Exxhyij8/ZWG9ytWqU+1utVudyYMar8SQgh/o1Br8Pd2RZ3Z1sq4PKP58UmvEZg+OPk43ESEhwWzV8NozHq4AMXV6wMeowGHbr3vLkdFkJ7zxK0zumMRReHVT5fHkRux2CMZ1z+IlhiH2KKeUS+Sv7EFzYxokxxvi5aGBdrR/SeeuLLR2JwdaFmDheVFOiN0MpaTRzXGx8/ZgVGO5U4pNIcj4zkhRKLGTNm0LNnT2xtbZkxY8Y/nqfT6SSxEEI8pdOplX2qVlWrRXl7Q61asHAh9OyZ8l8vMDyWnw7fAmBE85Kaze4sFgsz7Q9i7mngDbfG1Mmp3TCPAzMgIQYK1ATPpikfZDbi6wsTJsCyZfBkMcGuXdVKT6VKpWtoQogsyMbKQIEc9hTIYf/fJ9cpksSDZaDF69qH/2ELI5ukH87WXiix+Hv5k5RCCSGSq1YttSRtz57g5QVvvw3r16vJ3kWLptzXmb/nBjHxZioXdKVJKXdN+967e7n46CJ2xexp1XG8toNQPzixRB2/JqMVLysgACZNgh9+gLjHZQZt26r9KCpXTtfQhBBCpCKZkSiESBO5c8PWrfDVV6oUZt06KFNG1dxHRLx6/wFhMaw4ehtIerTCHBfHghNqs7vupbuTyy6JzRH2TwNTHBSuB0UbvXpQ2UxwsJovUawYzJ6tkoomTeDQITWvQpIKIYTI2pKdWLz11ltMmTJF8/h3331H586dUyQoIUTWZDCo0pgzZ9QLzthYmDhRlcWsWKFW0ntZ3+++TlyCmeqFc9CghHbVuqOLJzNo0kWaXjbSp1wfbQchvnDqZ3XcZJSMViRDRIT6PhYtqjZGjIpSo1Q7d6qVn+rUSe8IhRBCpIVkJxZ79+6lTZs2msdbtmzJvn37UiQoIUTWVqGC2lDv99/Vi1F/f+jVS030Pn48+f35hUSz6tgd4B9GKyxmQjduwi0cGjlVIYdtDm0n+74Dc7waqShS/2WeVrYTHg7Tp6sRii+/hNBQ9b3duFGtAtZUpqgIIUS2kuzEIiIiAmtra83jRqORsLCwFAlKCJH16XTQoQNcuqTq8R0c1IvRmjWhb1+4d+/F+/p+93XiTGZqF8tJXU/taMVfvn8xsnMsy9rY0fjDidoOgm7C6V/UcZPRL/mMso8bN2DYMPDwUHtPBAaCpyf8+qsajXrjDRnwEUKI7CjZiUX58uVZvXq15vFVq1ZRtmzZFAlKCJF92NqqzdGuXlWjFqBWESpZUm2sFxv7759/JyiK344/Ga3QLjVktpiZd3YeCVY6PHr2IYdrEhsm7P0OLCbwbAaFar3iM8qaLBZV2vTGG1CiBMyapUYsSpWCRYtUgti9u+wlKIQQ2VmyN8j76quv6NSpEzdu3OC1114DYNeuXaxcuZI1a9akeIBCiOzBwwN+/hkGDVL7Xhw7Bl98oV60Tp8O7dolfRd8zl/XSDBbaFDCjZpFc2ra/zq7gWvB13A0OtK7XG9tBw+vw7nHGyw0HpXCzyrzi4pS819mz4aLF5893qqV+j41by7JhBBCCCXZicUbb7zBhg0bmDRpEmvXrsXOzo6KFSuyc+dOGjWSVVSEEK+mdm1VErViBXz+uSq7ad9evYCdMQPKlXt27q2Hkaw75QeoXbafZ4qNwWHgWMa4mgj9tD0uNklsrLR3CljMULIVFKiWWk8r0/H1he+/V4ldcLB6zMFBlakNHiz7UAghhNBKdmIB0KZNmyQncAshRErQ6+Gdd9QcjEmT1IiFlxdUqqRGNMaNg5w5Yfaua5jMFpqUyk3VQtoJ2ft2LMYtPIECJh0tar2r/UIPrsD5teq4ycjUfVKZgMUCBw6oMqf168FsVo8XKwZDhqikwuWfN70VQgiRzb1UYgFw8uRJLl++jE6no2zZslSpUiUl4xJCCJyc1PKl770Hn3wCGzbAnDnwyy/w/qcRbAj9l9EKs4mZph2Evm9gYK43qOOUW/sF9kwGLFCmHeSrlLpPJgOLiYFVq1S50+nTzx5v2hSGDoU2bdRSwUIIIcS/SXZi8eDBA7p168aePXtwdXXFYrEQGhpKkyZNWLVqFblzJ/HPWwghXkHx4uoO+s6dajWiixdh4aFrOJQFl/A83DrlSpk8YDQ++5ztt7ZzM/QmTrmdadspidGI+xfg0gZ13Dh7jlbcvAlLl8KCBWplJwA7OzWJfsgQKF8+feMTQgiRuSR7yt2QIUMICwvj4sWLBAUFERwczIULFwgLC2Po0KGpEaMQQgDQrJlaznTi3HAcyvgDcHlNSdq3h4IF1ajGxYsQHxPNL/vnANC7bG+crJ20ne2ZrN6X6wB5ymnbsyCLRY1IjB2rysqKF4f//U8lFQULwpQpcOeOSjQkqRBCCJFcyR6x2LZtGzt37qRMmTJPHytbtizff/89LVq0SNHghBDieVZWcMfFG3RQr1Be8vZyZsUKCAiAadPU26fNJ/CZ3y22NLSjZ/ee2k78T8OVzYAuy49WJCSoeRMbNqi327eftRkM0LgxvP8+vPmmurZCCCHEy0r2vxGz2Yzx7/UGjxmNRsxPZvoJIUQqueQfxtYL99HpYGynkpTMo+60//mnKuvZsjUBT8NOrE3ge6kO/Xs70revmi/wdJ7AninqfYXOkDvrLW8UHQ07dqhE4o8/4NGjZ212dtCypUok2rZVk+CFEEKIlJDsxOK1117jo48+YuXKleTPnx8APz8/hg8fTtOmTVM8QCGE+LtZu7wBaFMhHyXzqBIno1EtSdu+Paw4/SffnI3mL29nNs74+unE5AIFoHdvGNjuFAW9t4FOD40+T8+nkqKCgmDzZpVMbN+u9p94ImdOtbHdm2+qZXvt7dMrSiGEEFlZshOLuXPn0r59e4oUKULBggXR6XT4+vpSoUIFVqxYkRoxCiEEABf9Q9l+MQCdDj5qWkLTnmBOYKXPAtDpaN59AJ90zMnSpfDrr3D3LkycCLVufEPBUnDNrgsJgZ6UcM2cJUBmM/j4qJGaDRtg714wmZ61FyqkEokOHaB+/cz5HIUQQmQuyf5XU7BgQU6dOoWXlxdXrlzBYrFQtmxZmjVrlhrxCSHEU7N3XQOgbcX8lMijnZC9Y89i/EJuk8M+J91Ld8feCNWrq3kXGzfCgd9O0a7UNkxmPW2++ZRrn4Otrdp0r1KlZ28VK0IO7bYY6cJiAX9/uHBBTUx/8v7iRYiMTHxuhQrPkonKlZPeqVwIIYRILS99D6t58+Y0b948JWMRQoh/9PfRiqGveWraY6MjyPHFHGbpTNwb1w5747N6H1tb6NoVupq+AW+4ZNWFXCU98T+vXpyfPKne/q5gQW2y4emZevs5WCzw4EHi5OHJ+9DQpD/HaISaNVUi0b69ik8IIYRILy+UWMyePfuFO5QlZ4UQqeG/Rit27v+ZHCYTRoOedg37azvwOwWP51ZUGPQph8eocqIbN+DsWTh3Tr0/e1atnHTnjnrbvPlZF/b2ahnWJ4mGu7tKCODf3yf1WEKCjqNHi7B9u55Ll1QC8fBh0s/dYIASJdTXLldOvZUvrxKJJNbSEEIIIdLFCyUWM2bMeKHOdDqdJBZCiBT3X6MV8aZ45oRv4sEHBr7I15u6Dq7aTvZ+o95X6AJuqg+9Xr1gL1EC3nrr2akhIXD+/LNE49w59XFUFBw7pt5enRWQeLdvnU7tLfEkcXiSRJQqBTY2KfE1hRBCiNTzQomFj49Pasfxn4KDgxk6dCibNm0C4I033mDOnDm4urr+4+f06dOHn376KdFjtWrV4siRI6kZqhAihf3XaMXGGxvxi/Ajl5Mb7V4frO3gb6MVNPz0P7+eqys0aKDenjCZ4Pr1Z4nGuXMQFqbansxl0OkSH//bY2AmODiABg3cqVTJQLlyULq0rNgkhBAi83rpORZxcXH4+PhQvHhxrNJguZEePXpw9+5dtm3bBsCAAQPo1asXf/zxx79+XsuWLVm6dOnTj62trVM1TiFEyvrPuRVREezYPAdywbsV3sXOyk7bSRKjFcllMKiRg1KloEuXl+oikfh4E3/+eYzWrVtjNKbSxA0hhBAiDSU7I4iKimLIkCFPRwK8vb0pVqwYQ4cOJX/+/HzxxRcpHuTly5fZtm0bR44coVatWgAsWrSIOnXqcPXqVUqV+ucNrmxsbMibN2+KxySESBv/NVpxYP4Yhi96QK2qdnTu2VnbQTJHK4QQQgjxcpKdWIwcOZKzZ8+yZ88eWrZs+fTxZs2aMXbs2FRJLA4fPoyLi8vTpAKgdu3auLi4cOjQoX9NLPbs2YO7uzuurq40atSIiRMn4u7u/o/nx8bGEhsb+/TjsMe1DvHx8cTHx6fAs0meJ18zPb52ViPXMmWk5XW8dC/s6WjFBw2LaL5mnCmO81f3466H/NUbYbAYNOcYdk9GD5jLv4XJpTBkkO+//DymHLmWKUOuY8qRa5ky5DqmjFe9jsn5PJ3F8mSdkhdTuHBhVq9eTe3atXFycuLs2bMUK1aM69evU7Vq1acvxFPSpEmTWLZsGd7e3okeL1myJH379mXkyJFJft7q1atxdHSkcOHC+Pj48NVXX5GQkMDJkyex+YeZkOPGjWP8+PGax3/99Vfs06H42fH8eZxPnCSkXl2iSpZM868vRHpafFXPuSA9VXOZ6V3SrGk/GnuUP6L/oFioA+/kH4aVMXEZlGvUTRpdHYcFHbvKTCHSNl9ahS6EEEJkCVFRUfTo0YPQ0FCcnZ3/9dxkj1gEBgYmecc/MjISXTJ3Y/qnF/F/d/z4cYAk+7ZYLP/6Nbt27fr0uHz58lSvXp3ChQuzZcsWOnbsmOTnjBw5khEjRjz9OCwsjIIFC9KiRYv/vJipIeDkKcKvXCFPqVLkG9Y6zb9+VhIfH4+XlxfNmzfHKGt0vrS0uo6X7oVx7vARdDr4X4/6lHB3TNQea4pl9ia1FHbnpoN5o2QnTR+G1T0AsFToTKM33k21WF+G/DymHLmWKUOuY8qRa5ky5DqmjFe9jskZNEh2YlGjRg22bNnCkCFDgGcv+J/MeUiOwYMH061bt389p0iRIpw7d46AgABNW2BgIHny5Hnhr5cvXz4KFy7MtWvX/vEcGxubJEczjEZjuvxQu3R4E5/gIAr16yu/VCkkvb6XWU1qX8d5e9VqdG0r5qesh3Yb7C2bphIbGEAe97x0Kd0Fo+G5WPxOwfUdoNOjb/Q5+gz6PZefx5Qj1zJlyHVMOXItU4Zcx5TxstcxOZ+T7MRi8uTJtGzZkkuXLpGQkMCsWbO4ePEihw8fZu/evcnqy83NDTc3t/88r06dOoSGhnLs2DFq1qwJwNGjRwkNDaVu3bov/PUePXrEnTt3yJcv85RD2JYvT1CzZlgXK5beoQiRZv5rJaioiBDyTFnB3Ggzdye2wtqQxGpvKbASlBBCCCFenP5FTzxz5gwAdevW5eDBg0RFRVG8eHF27NhBnjx5OHz4MNWqVUuVIMuUKUPLli3p378/R44c4ciRI/Tv35+2bdsmmrhdunRp1q9fD0BERASffPIJhw8f5tatW+zZs4d27drh5uZGhw4dUiVOIUTK+K+VoDYfX8EDJzORDgZatPhA24GsBCWEEEKkuRcesahatSpVqlThvffeo0ePHpqN51LbL7/8wtChQ2nRogWgNsibO3duonOuXr1KaGgoAAaDgfPnz/Pzzz8TEhJCvnz5aNKkCatXr8bJSftCJUMzm4k+c5bgAwfIPXQIOoOseS+yrv8arYhOiGZ+4DoevmNgQqnhWNslsaiCjFYIIYQQae6FE4uDBw+yZMkSvvjiCz7++GM6depEv379aNKkSWrG91TOnDlZsWLFv57z9wWu7Ozs2L59e2qHlTYsFu59+CHmsDAc6tbFoVbN9I5IiFTzX6MVv139jYfRD/FwKkDbmu9oO5DRCiGEECJdvHApVJ06dVi0aBH3799n/vz53Llzh2bNmlG8eHEmTpzI3bt3UzPO7M1gwKldW5zbtsXg5Pjf5wuRSf19tOKjptqRhoiwR1xc8T0Gk4UBFQdoJ2zDs9GKil1ltEIIIYRIQy+cWDxhZ2dH79692bNnD97e3nTv3p0FCxZQtGhRWreW5VBTS+4vvsBj6nfYli2b3qEIkWqejFa0q5gfT3ftaMX+77+i7/pwxq8z0q54O20HMlohhBBCpJtkJxZ/V7x4cb744gtGjx6Ns7Nz1ik9EkKkuURzK5IYrYiKj2Jf0HFC7cG5TWuM+v8YrchVPJUjFkIIIcTfJXu52Sf27t3LkiVLWLduHQaDgS5duvDuuxlrA6qsKCEoiHhfX+wqV07vUIRIUf81WvHrlV/ZXD6GK9WK8FuHL7UdyGiFEEIIka6SlVjcuXOHZcuWsWzZMnx8fKhbty5z5syhS5cuODg4pFaM4rGokye53esdrPLkwfOvXcne6VyIjOq/Risi4iJYdnEZAP1qDMJoY6ftREYrhBBCiHT1wolF8+bN2b17N7lz5+add96hX79+ifaQEKnPtlw59La2WOXIgenRI6xeYHNBITKD/xqt2P7zBNwCQ8hRuiitirbSdiCjFUIIIUS6e+HEws7OjnXr1tG2bVsMso9CutDb2lJ8106scuRI71CESDH/NVoRGvKAAvM2MznKwr2vm2ClT+LPloxWCCGEEOnuhROLTZs2pWYc4gVJUiGymv8arVhzfjlxxaH8PSMN23+o7UBGK4QQQogM4aUnb4v0ZTGZsMTGordPYtdhITKJ/xqtCIsLY8mddYS3NfBdnYlYWdtoO5HRCiGEECJDeKXlZkX6CFm7lmuNG/NwwcL0DkWIV/JfoxXLLy0nPD4cT1dPWpRoo+1ARiuEEEKIDEMSi0xIZ2uHKfAhkYcOpXcoQry0/xqtCA6+R8T3i3CKsjCo8iD0uiT+XMlohRBCCJFhSClUJuTYuDEFFy3EoVat9A5FiJf2n7tszxrFG/tjqX7DlsYDX9N2IKMVQgghRIYiIxaZkMHRAccGDdBZW6d3KEK8lP8crYgJZoPhHDfygl3Pzhj0SaxEJ6MVQgghRIYiIxZCiDT3X6MVyy4u43ihOCJGlGdVm8+1HchohRBCCJHhyIhFJha8ahW33n6b2Bs30jsUIV7Yf41WPIp+xMorKwEYVOVD9EntmyOjFUIIIUSGI4lFJha+ezfRJ04SvmNHeocixAubufPfRyt2zhtJ9dORlHctS6MCjbQd+J2U0QohhBAiA5JSqEwsZ8+eONarh1OLFukdihAv5NzdELwuBaDXwdCmJTTtDwJvU2zFfipGQ2jV2uh0Om0nf01U7yt2k9EKIYQQIgORxCITc2zYEBo2TO8whHhh0728AXizsgee7o6a9uVXfyG4lp6Gt+xo1mWItgPfI3BjF+itoNFnqR2uEEIIIZJBSqEysOg4E7P/us7UcwZiE8wv14nPPljZA44tStnghEimk7eD2XM1EINel+RoRWBUICtv/c7GOnocfpyJ3iqJ+x5//U+9r9wTchZN5YiFEEIIkRySWGRg1lZ6fjvhx51IHXu9A5M8xxIfT8SBgzycPz/pTh5cgatb4PSKVIxUiP823esqAG9VLUARNwdN++ILi4k1xVI5d2XqetTTduCzD27tB4O1zK0QQgghMiBJLDIwg15Hu0r5ANhw5l6S55hCQ7kzYACBs2YT7+enPaF8R1U2cu8MBF5NxWiF+GdHbj7i4PVHGA06hiSxEtT9gJvk/mYFRe+rXbY1cysslmdzK6r2BteCaRC1EEIIIZJDEosMrv3jxGKPdyAhUXGadis3N5xeb4Frt65YLEl04OAGns3U8dlVqRipEEmzWCxM36HmVnSrUYgCOew15xycOZK6F0188qc1tfImsaP8jV1w5whY2UKDj1M7ZCGEEEK8BEksMrjSeZ3Ib28h3mRhy/mkRy0KzJhBvnHjsC7gkXQnFbuq9+fXgPkl52oI8ZIOXH/IsVtBWFvp+bCJdrTiXsQ9luS5yv5yOhwH9kWvf+7P0t9HK2q8B8750iBqIYQQQiSXJBaZQHU3lQysP5VEqdOLKNUKbJwh9A74HkrByIT4dxaLhamPRyverlWYvC62mnMWnV+Ebw4TRwbUpmqPJFaCuroV/E+B0QHqDUvliIUQQgjxsiSxyASquVnQ6eDE7WB8H0X943lxd/2IvnhR22C0g7JvqONzq1MpSiG0/rrygLN3QrAzGvigsXbPCb8IP9ZfXw/AoEqDtB2YzbB7kjquNQAcc6dmuEIIIYR4BZJYZAKuNlCnWE4ANpxJetQidNMmbjRrRsDkyUl38qQc6uJGiI9JjTCFSMRisTzdt+KduoXJ7WSjOWfftx/TaXcsjZyrUj1vdW0nlzdBwHmwdoK6Q1M7ZCGEEEK8AkksMoknk7g3nPbDksQsbfvq1cFgQGdlxBIfr+2gcH1wLgCxoeC9LbXDFYLtF+9z0T8MB2sDAxtqRyt8712hxMazdDpkoX9sbW0HZhPseZwo1xkE9jlTOWIhhBBCvApJLDKJFmXzYGvUc/NhJGfvhmrajfnzU/LgAQovW4rOaNR2oNdDxc7qWMqhRCozmy3M8LoGQL/6RcnpYK05Z9GNFcxrq+dq1dxU7DJQ28mF3yHwCti6QO0kyqSEEEIIkaFIYpFJONpY0aJsXkCNWiTF4Or67508KYe6tgMiH6VgdEIktvn8Pa4GhONka8V79Ytp2n3DfPnj5maOl9RTdNYcdM+vBGVKeDZaUXcI2LmmftBCCCGEeCWSWGQiHaqq5WT/OOtPvOmfl401x8VhjkliHoV7GchbEcwJcPH31ApTZHMJJjMzd6q5Ff0bFMPFXjuCtuDcAkwWE/U96lMpdyVtJ+dWQ9ANsMsJtd5P7ZCFEEIIkQIkschEGni64eZozaPIOPZ5ByZ5TuCcuVyrW4/QP/5IupMnoxZSDiVSycYz/twMjCSHvZG+9Ypo2m/eOUfNseupe8nMhxU/0HaQEAd7v1HH9YeDjVPqBiyEEEKIFCGJRSZiZdDTrlJ+ANb/QzmUzmjEHBFB1OEjSXdS4S3Q6eHucXh0I7VCFdlUvMnMrF1qbsXARsVxstWOVhyeM4aSfhbePmFPObfy2k7OrICQ2+CYR22IJ4QQQohMQRKLTKZjlQIAeF0KICxGu/qTS4c3Kfzrr+Sf+l3SHTjlhWKN1fG531IpSpFdrT15F9+gKNwcrXmnTmFN+5WgK8zyvM7qBnrcPhqqnVsRHwP7pqrj+iPA2j4NohZCCCFESpDEIpMp7+FM8dwOxCaY2XbhvqbdmCcP9lWraF+w/V3Fbur9udWQxNK1QryM2AQTcx6PVnzQ2BN7ayvNObNOzSLaRkfU220o80YvbSenfoIwP3D2gGp9UjliIYQQQqQkSSwyGZ1OR8eqatRi/amky6H+U5m2YHSAYB9VEiVEClh9/A7+oTHkcbahZ61Cmvbjfkc54HcAK50Vg6sM1nYQFwX7p6njBh+D0TaVIxZCCCFESpLEIhNqX1nNszji8wj/kGhNuyUhgYfz5+PTuQumiAhtB9YOKrkAmcQtUkRMvIm5f10HYHATT2yNhkTtFouFGyM/5uN1Jt5xakYhZ23iwYnFEBEAroWgShKjGUIIIYTI0CSxyIQK5LCnZtGcWCxqBZ7n6aysCP1jMzHnzxOxe0/SnTxZHerCOrUKjxCvYMWR2zwIj8XD1Y4uNQpq2ved3Ui5E4+o5W2hS77W2g5iI+DADHXc8DOw0m6oJ4QQQoiMTRKLTKpjFbWnxfrTd7EkMU/C7f2B5Js4EccG9ZPuoGgjtepOdDBc90rNUEUWFxWXwA971QpjQ17zxMYq8WiFyWxi5u2f+KyfgavdauFRu4m2k2MLIOoR5CwGlbqnRdhCCCGESGGSWGRSrSrkw9pKj3dABJfuhWnaXd54A9dOHf95N26DFVTorI6lHEq8gp8O3eZhRByFc9nTqVoBTfsWny1cD7lOqIczTUbO0nYQEwoHZ6vjxiPVz6YQQgghMh1JLDIpFzsjzcq4A68wibtiF/X+6jaIDkmZwES2Eh4Tz4J9arTio6YlMBoS/0mJM8Xx4+E5ALxb/l1cbFy0nRyeBzEhkLs0lO+U2iELIYQQIpVIYpGJdXi8p8XGs/6YzNpyKHN0NGHbthP401Ki4qO0HeStCLnLgCkWLm1M7XBFFrTkwC1CouIpntuB9pU9NO1b133H2O/u0uO4HT3K9NB2EBUER+ap48ZfgN6gPUcIIYQQmYIkFplYo5K5yWFvJDA8loPXH2raY6/fwG/YMPymfcfPpxZpO9DpoNLjSdxSDiWSKTQ6nh8P3ARgWLOSGPS6RO2R8ZEErl+LfSw0sC6DnZWdtpNDcyA2DPKUhzLt0yJsIYQQQqQSSSwyMWsrPW0rqqVnN5zWlkPZli9HdCVPtlWFLZc3kGBO0HZSoTOgg9sHIcQ3lSMWWcnig7cIj0mgdF4n2lTIp2lffmk5s1+PZ3k3d6p9PkXbQeRDOLpAHTcZBf+2qaMQQgghMjz5T57Jvfl4dahtF+8TFZc4cdDpdJT/dR1bW+Xmlu4he+/u1XbgUgCKPF456txvqR2uyCIi4uHnwyoRHdasJPrnRiuCY4JZdnEZFp2Ohr1HYpdHm3hwYAbER0L+KlAqiSVohRBCCJGpSGKRyVUt5ErhXPZExZnYfvG+pt3aYM2bnm8CsObqmqQ7qfi3cqgklq4V4nm7/PVExpko7+HM6+XyaNp/+WsGUbERlMlZhhZFWmg7CL8Px39Ux01Gq7I8IYQQQmRqklhkcjqdjjcrP9nTQrtZHsBbJd+iSACEH9jPnbA72hPKvgFWtvDQG+6dScVoRVYQGB7L/vsqERjRvCS655IC/2BfKkxYy3dLTAzP3RW9Lok/M/unQ0IMFKgJns3SImwhhBBCpDJJLLKADo/LoQ5cC+RBWIym3fXoVb5dksB7282suZpEuZOtC5RqpY7PyiRu8e8W7Pch3qyjckEXmpRy17Sv3vod9jEWcsUYqVmhpbaD0Ltwcqk6fu1LGa0QQgghsghJLLKAIm4OVC3kitkCm85qRy0c6tbF5OLIjXw6tl9YT5wpTttJxW7q/YW1YEpikrcQgF9INCuP3wVgWFNPzWjFzZCbLEvYx5D3DVh/+xUGBwdtJ3u/AVMcFGkAxRqlRdhCCCGESAOSWGQRT0Yt1iexOpTe3p6Su3ezskc+/PWh7Ly9U9uBZ1OwzwWRgXBzd2qHKzKpqduvEpdgxtPZTN1iOTXtc07PwWwxU6tkUyo26azt4MFlOL1CHb/2VSpHK4QQQoi0JIlFFtG2Yn6s9Dou+ofhHRCuabe2d+StEm8B8Jt3EuVQBuOzXY9lTwuRhAt+oU8T1zcLmzWjFedvHuHacS/0Oj1DqgxJuhOvMWAxQ5k3oFCt1A5ZCCGEEGlIEossIoeDNY0f17snNWoB0LFER1yi9YSdOsH14OvaE56UQ13eDLHa5ERkXxaLhYlbLgPwRsV8FHTUtp+Y/iXfLDEx+lwxPHN4aju5uQeu7QC9FTQbl+oxCyGEECJtSWKRhXSsqsqhNp72w2zWLhvrdNWf+XMTGL7exNrLSYxKeFSFnMUhIVolF0I8tvvqAw7ffIS1lZ4RzbVJw+F7h4l+4I8eqNW4u7YDsxl2PC59qv4u5CqeugELIYQQIs1JYpGFvFbaHSdbK/xDYzjqE6Rpty1fDr29PeH2sP/sH0TFRyU+QaeDSo9HLc6tSoOIRWaQYDIz+c8rAPStWwQPV7tE7WaLmVmnZjG/jYHdk9pTqE0ScyvO/wb3z4GNMzT6PC3CFkIIIUQak8QiC7E1GmhTQe1wvP70XU273toaz02bmDOkML72kWy/tV3bSYXHLwpv7oWwpPfFENnLmpN3ufYgAld7I4OaaEcrvG57cenRJeyt7OnW+jPN3Avio2HX1+q4/nBwyJUGUQshhBAirUlikcU8WR1q6/n7xMSbNO02efPRuXQXAH5Lak+LnEWhYG3AAufXpmaoIhOIjE1gupc3AENfK4GLnTFRe7w5nj3LJ2MXY6FPuT7ktNWuFMXRHyDsLjgXgNofpEXYQgghhEgHklhkMTWK5MTD1Y7w2AR2Xg5I8pw3Pd/EGiseeZ/n4qOL2hMqdVXvZXWobG/hvpsEhsdSOJc9b9curGnf9tdC3v4lgO9/MNMz/xvaDiIfql22AZp+BUY77TlCCCGEyBIkschi9Hodb1bJD8CGf1gdysE/lB9+0DH+FxNrLyaRPJR9EwzWEHAB7l9IxWhFRvYgLIaF+24C8NnrpbG2SvznIiYhho1nVuGfC+IrlcTZ3UPbyd5vITYM8laECl3SImwhhBBCpBNJLLKgJ+VQe64G8igiVtNuXbAADjprDCY4d2IL4XHPLS1rnxNKtFDHMmqRbc3Y6U10vIkqhVxpXSGvpn2192qO5g5h6kcFqDJtkbaDRzfgxGJ13OJr0MufGyGEECIrk//0WZCnuxMVPFxIMFvYcv6epl1nNFJ08VK+HV0C71xxbL6ZxNKyFR+XQ51fC2btXA2RtXkHhLP6+B0ARrcuo5mQHW2OZumlpQAMqjoYu1y5tZ3sHAfmBJWkFmucyhELIYQQIr1JYpFFPRm1+P1U0uVQdmXK0KG8Sh5+u/obFstz+16UfB1sXSHcH27tT81QRQY0ZesVzBZoWS4v1YtoJ2Rfv7aZMudCKO5cjLbF2mo78D0KlzeBTg/NJ6RBxEIIIYRIb5JYZFHtKuXHoNdx5k4INwMjkjznjeJvYGdlx7171zj94HTiRisbKNdBHZ+Vcqjs5ND1h/x15QFWeh2ftyqtaQ+MCqTS1lN8vN7MyOtlMOgNiU+wWGDHl+q4ytvgXiYNohZCCCFEepPEIovK7WRDgxJuAGw4k/R+FHahMXy7xpZZC0ysvbhSe8KTcqjLmyAuStsushyz2cLEPy8D0LNWIYq6OWjOWXJ2IaeLQbiTFVX7fKzt5NJGuHsMjPbQZHRqhyyEEEKIDCLTJBYTJ06kbt262Nvb4+rq+kKfY7FYGDduHPnz58fOzo7GjRtz8WISy6tmUU/KoTac9tOWOgGGnDlxD7LgGAO+B3cQHBOc+IRCtcG1EMRFwNU/0yJkkc42nvXjon8YTjZWDG1aQtPuE+rDulsbWdPQgHn1PIy5n5tbkRCn5lYA1B0CTtpJ30IIIYTImjJNYhEXF0fnzp354IMX32Dr22+/Zfr06cydO5fjx4+TN29emjdvTnh4+H9/chbQomxeHKwN+AZFcco3WNOuMxgoPHUaM0eX5mwhMxuvb3zuBN2zUQtZHSrLi4k3MXW72gzvgybFyeVok6jdYrHwzbFvSLAkUMqqFNUK1tZ2cmIJBPuAgzvUHZoWYQshhBAig8g0icX48eMZPnw4FSpUeKHzLRYLM2fOZPTo0XTs2JHy5cvz008/ERUVxa+//prK0WYMdtYGWpbPB8Dak3eTPMehZk1a1nwbgDXeazBbzIlPeJJYXN8F4fdTLVaR/pYevIVfSDT5XWzpV6+opn3PxT+oNn8fBUIMtLZrre0gOgT2TlHHTUaBjWPqBiyEEEKIDCXTJBbJ5ePjw/3792nRosXTx2xsbGjUqBGHDh1Kx8jSVpfqBQC1OtTDJPa0AGhVtBWORkfuht7m6L2jiRvdSkDB2mAxwZH5qR2uSCdBkXHM230dgI9blMLWmHhCdkxCDNe++x/1L1kYu82ZXHrtSlEcmA7RweBWCqr0SouwhRBCCJGBWKV3AKnl/n11dz1PnjyJHs+TJw+3b9/+x8+LjY0lNvbZC/CwsDAA4uPjiY+PT4VI/92Tr/myX7tKAScqFXDh7N1QFu+/wYhm2rp5Q1Q8X+51w/VkCGvzrqB67uqJ2nW1P8TqzhEsJxaTUHso2Dq/VCzp7VWvZVY20+sq4bEJlMnrRNvy7pprtPj8YjZWiiJnkA31RnxFQFhU4nNC72B15Ad0QMJrY7CYLWCW6/xv5Ocx5ci1TBlyHVOOXMuUIdcxZbzqdUzO56VrYjFu3DjGjx//r+ccP36c6tWr/+s5/+b5jb0sFovmsb+bPHlykjHt2LEDe3v7l47jVXl5eb3051az13EWA8sO3KRI9DVsn1sdFLOZghceYhcBUbv3sipmFc76vyUPFjNNbD1wjvHDe+VIrudp89KxZASvci2zosBoWHHWAOhokiOEbdu2JmoPNgfzY9iPJOTSceWdtzCGqRXC/n4dq976gYKmWAIdy3DIOwGuyWT/FyU/jylHrmXKkOuYcuRapgy5jinjZa9jVNSLrwyaronF4MGD6dat27+eU6RIkZfqO29etRrN/fv3yZcv39PHHzx4oBnF+LuRI0cyYsSIpx+HhYVRsGBBWrRogbNz2t+pj4+Px8vLi+bNm2M0Gl+qj5ZmC3vmHOTmwyhCcpalX70imnMinZ359tIcDjhdp0LhcLpVSPx90RUIh81DKBu6m5K9poGV7UvFkp5S4lpmRUNWncVsCaBRCTeG96iqaf9s7yckhCVQ3b06nzX9jISEhMTX8d5ZjKdVeaFrlzm0zlc5jZ9B5iQ/jylHrmXKkOuYcuRapgy5jinjVa/jk+qdF5GuiYWbmxtubm6p0nfRokXJmzcvXl5eVKlSBVArS+3du5dvvvnmHz/PxsYGGxsbzeNGozFdf6hf9esPbFScz9edZ+khX/rWL461VeLpNa5Nm1K3aDR/7B/J7zd+Z0DlAVjp//bjUbkb7JuCLswP46V1UK3PS8eS3tL7e5mRnLwdxLaLAeh1MKpNWc11OeKzl9Zjd+Bc3kCPCZ9gbW39dMTPaDRitLKCv8apkyt0wVioRho/g8xPfh5TjlzLlCHXMeXItUwZch1Txstex+R8TqaZvO3r68uZM2fw9fXFZDJx5swZzpw5Q0TEs12lS5cuzfr16wFVAjVs2DAmTZrE+vXruXDhAn369MHe3p4ePXqk19NIN29W8SCPsw33w2LYcMYvyXNaFG5BDpscBEQFcMDvQOJGK2uoPUgdH5wNZlMqRyxSm8ViYeIWtRle52oFKZXXKVF7vDmeXQvHUOARvHHRlhIuxbWdXNsBt/aDwQaafpUWYQshhBAig8o0icWYMWOoUqUKY8eOJSIigipVqlClShVOnDjx9JyrV68SGhr69OPPPvuMYcOGMWjQIKpXr46fnx87duzAyckpqS+RpdlYGZ4uIbpg7w3MZu2GeUazjmHexfhmSQLrz/yi7aRab7B1haAbcGVzKkcsUtu2C/c55RuCndHAiBYlNe0rL69kValH/NjRiQJjJ6C3fa78zZwAXmPUca2BajNFIYQQQmRbmSaxWLZsGRaLRfPWuHHjp+dYLBb69Onz9GOdTse4ceO4d+8eMTEx7N27l/Lly6d98BlEj1qFcLK14kZgJDsvB2hPsLKi7OF7FA0Ao9ch7oY/t/eFjRPU7K+OD8yEJHbzFplDXIKZb7ZdAaB/w2LkcU6cNDyMfsj8s/NBp6Nun8/J01y7b4Xu7K8QeAXsckCDj9MkbiGEEEJkXJkmsRCvzsnWSK/ahQGYv/cGlucSA51OR/6PRuDVrQR7KuhYd22dtpOaA9XEbf9TqgRGZEq/HL3NrUdRuDnaMLBhMU37wh2TiIoNp1yucnQo0UHTbjDFYHiyGV6jz8HONZUjFkIIIURGJ4lFNtO3XlGsrfSc9g3hmE+Qpt255euU7TuUWGsdv1/7nXjTc2sXO+aGKmqnbg7MSIOIRUoLjY5n9q5rAAxvXgIHm8RrOJy9d4pq323l2yUmRuV5B71O+2fC88Gf6CIfQI6iUP3dNIlbCCGEEBmbJBbZTG4nG96qpnbj/mHvjSTPaVSwEe527gTFBLHrzi7tCXUGg04PN/6Ce2dTM1yRCubvuUFwVDye7o50rV4wUZvZYubHzePJEQHu0daUK1lP20H4fTwfPN6notlYNbFfCCGEENmeJBbZ0IAGxdDrYPfVQK7c165NbKWzYkBYFT5bY+KPk0lM4s5ZFMo9Lo85OCuVoxUpyS8kmiUHfQD4omVprAyJ/wSsv7aePdY3GTXEmTyzpmNwcdH0Ydj3DVbmOMwe1aHsm2kRthBCCCEyAUkssqEibg60Kq82DVyw92aS51TZ7E316xacd53iZmgS59Qbpt5fXA9BPqkUqUhpk7ZcJi7BTO1iOWlaxj1RW2hsKLNOqUTxndofkr9eU20H/qfRnVXJprnpePiXXeyFEEIIkb1IYpFNvd9I7Umw6aw/d4MTb9Wu0+nI895ATjcrzPGSOtZcXaPtIF9FKN4ULGY4PDctQhavaOelALacv4dBr+OrtmWfbnT3xPLNk8hxK4hiLsXoXqa7tgNTAmwais5i5m6O2lgK1kqjyIUQQgiRGUhikU1VKOBCfU83TGYLP+7Xjji4tG1DwS9GE5BDx8YbG4lJiNF2Un+Yen96BUQEpm7A4pVExCbw1cYLALzXoCjl8icucboadBWP+X8waZmJMYF1MeqT2GXzyDy4fw6LrSsXPHqmRdhCCCGEyEQkscjGnoxarDruS1BknKa9nkc9PBw9CI8LZ/ut7doOijSA/FUhIQaO/pDa4YpXMHX7Ve6FxlAopz3DmibeDM9isTD1wEQeuIDJxkDFdr21HQTfgt2TADA1HU+sUTv3QgghhBDZmyQW2Vg9z1yU93AmJt7MT4duadr1Oj297JrQx8vEn8eTmMSt0z0btTi+CGLDUzVe8XLO3Anhp8O3AJjYoTx21oZE7dtvbedI8GkWdbAnx8aVGPPmTdyBxQKbR0BCNBRpgKVSjzSKXAghhBCZiSQW2ZhOp3s6avHT4VtExSVozqm57AStT1jIs+cipwJOaTsp3RZyFoeYUDj5U2qHLJIp3mTmi3XnsFigYxUPGpTInag9Kj6KqSemAvBu+XcpWKSCtpPza+DGLjDYQNuZMmFbCCGEEEmSxCKba1U+H4Vz2RMSFc/q43c07e693sGvigdXCuiYdnKaZrdu9Aao95E6Pvw9JGhLqkT6WbT/Jlfuh5PD3sjoNmU07b/snE6LP/wpbpWPvuX7ajuICoJtX6jjRp+Cm2cqRyyEEEKIzEoSi2zOoNfRv0ExAH7c70O8yZyo3aVdOyotXsmtYvacCzzHTt+d2k4qdQPHvBDur+5uiwzh1sNIZu1UO2x/2aYsuRxtErX7hvliM38l7Y5ZGLMvN7ZWttpOdnwJUY/AvSzU/SgtwhZCCCFEJiWJheCtagVwc7TGLySazef8Ne257XPTu5ya0Dvz5EziTfGJT7CygdofqOODs8BsRqQvi8XC6A3niU0wU9/TjY5VPTTnfHv8W3ZUgYf57Cn7yThtJzf3wplfAB20myU7bAshhBDiX0liIbA1GuhbrygAP+y5qS13Anp7dqfrCRvK7LnFGu8kRiWq9wUbZ3h4Fby3pnbI4j+sO+XHweuPsLHSM7FDec2eFfvu7mPv3b1cLG5N/vW/YVuiROIO4qPhj8cjFDXeg4I10yhyIYQQQmRWklgIAN6uXRhHGyuuBoSz++oDTbtpz2E6eUXSba+Z5YfnEREXkfgEWxeo3k8dH5ipVhIS6eJRRCz/23IJgGHNSlI4l0Oi9jhTHN8cnQJAzzI9Ke5aXNvJ3m8h2Aec8kPTMakesxBCCCEyP0ksBAAudkZ61CoEqFGL5zm3aol944ZsbueOny6EJReWaDup/QEYrOHuMfA9nNohi3/wvy2XCYmKp3ReJ95rUFTTvvLwDwye5UPzm44MrDhQ28H9C3Botjpu/R3YOqdyxEIIIYTICiSxEE/1q1cUo0HHsVtBnLwdnKhNZzBQ+IcFNBgwBotex/JLywmIDEjcgVNeqPx4j4MDM9MmaJHIPu9A1p/2Q6eDKZ0qYjQk/hUPiAzg4eIfKfIAep1wwNHKPnEHZpMqgTInqKWEy7RNw+iFEEIIkZlJYiGeyutiS4cqapLvD3tvJHnOawVfo4p7FWISovn+zPfaE+oOBXRwbTsEXErFaMXzouISGL3hPAB96hahckHXRO0Wi4X/Hfkfv9Yzs69FPkp+/Q06Q+LN8jj+I/idUPNlWn+XRpELIYQQIiuQxEIkMqBhcXQ68LoUwPUH2p20dTodn+heZ/IyE+cPrMc72DvxCbmKQ9k31PHBWWkQsXhi1s5r3AmKJr+LLR+3KKVpX+O9hj1392CxsabxuPk4VK2W+ITQu7BrgjpuNhac86dB1EIIIYTIKiSxEIl4ujvSvEweAH7Yq51rAeC2+xzF70On/SZmnpypPaHeMPX+/BoI8U2dQEUiF/xC+fGADwAT2pfH0cYqUfvN0Jus2TQFLBY+qvoRpXI+l3hYLLDlE4iLgIK1oFq/tApdCCGEEFmEJBZC4/3GapWgjWf8uBcarWnP/dFHWHVtz8I21uz328/Re0cTn+BRFYo2BItJ7cYtUpXJbGHk7+cxmS20qZCPZmXzJGqPN8WzYMlgJiyO5uttOXi7ZHdtJ5c3qWWC9Ua1Z4Ve/jQIIYQQInnk1YPQqFooB7WK5iTeZGHxfh9NuzF/fkqMn0LLql0AmHZiGmbLc5vi1R+u3p/6GaKCUjvkbG3pQR/O+4XiZGvF2DfKatq/P/M98bduk6CHisXqYDA+t9FddAj8+ak6rj8c3MukftBCCCGEyHIksRBJejJqsfKYL6FR8UmfU+l9HIwO3Lx/ia0+z22KV6wJ5K0I8VFwbGFqh5tt3QmKYtoONc9lVOsyuDvZJmo/fv84Sy4swauqnkdzPqXI6LHaTnaOg4gAyOUJDT5Og6iFEEIIkRVJYiGS1LhkbkrndSIyzsTyI7eSPMclzorJBwoyY5GJ+UdmEmeKe9ao00H9Yer46AKIi0z1mLMbi8XCVxsvEB1vomaRnHStXjBRe2hsKKMOjMKChQ6eHWjctB96h8Sb5XH7MJxcqo7bzQJj4sRECCGEEOJFSWIhkqTT6Xi/kRq1WHrwFjHxJu05trYUuBqEWxjkO+fPyisrE59Qpj3kKALRQXB6RRpEnb1sPnePPVcDsTbomdSxAnq97mmbxWJh5p+j6b7Cj3KWfHxR8wttBwmxas8KgCq9oEj9NIpcCCGEEFmRJBbiH7WtmA8PVzseRcax5sQdTbve2pp8EyZw+9uBHCmjZ8G5BYTGhj47wWAFdYeo40NzwJR0SZVIvpCoOMb/cRGAD5t44unumKh9883NeP74F3WuWPhqjxv2RnttJwdmwMOr4OAOLb5Oi7CFEEIIkYVJYiH+kZVBT/8GRQFYuP8m8Saz5hzHevVo3nYInq6ehMeF8+P5HxOfULknOOSG0DtwYV1ahJ0tTP7zCg8j4vB0d+T9xsUStflF+DHp6CR+bqonpKwHJcZP1nYQeBX2T1PHraaAXY40iFoIIYQQWZkkFuJfda1RiJwO1twJimbhvqT3tTDoDYyoNgLbWAubj6/AL8LvWaPRDmq9r453joPo4NQPOos7fOMRqx+PIE3uWAEbq2e7Z5vMJkbtH0VEfATupatQY+02rAsXTtyB2Qx/DANTHJRoAeU6pmH0QgghhMiqJLEQ/8rO2sCXbdTyozN3enP1vnY3boDKN8zMX6Sn1/ZY5p6em7ixzodqxaHwe7B9dGqHnKXFxJsYvf48AD1qFaJGkZyJ2pecWsDdqydxMDowucFkrPRW2k5O/wy+h8BoD22mqYn2QgghhBCvSBIL8Z86VPGgWRl34k0WPl17loQkSqKM+fJhH2miSICFXZf/4NKjS39rtIP28wAdnPkFvLenXfBZzPe7r3PzYSTuTjZ83rJ0orbzgecJnT2PqYtNTI5uRQGnAtoOwu/DjjHq+LUvwbVQGkQthBBCiOxAEgvxn3Q6HRM7VMDZ1opzd0NZkERJlG3JkhT+cRFeE9sSbaNj+onpWCyWZycUqqVGLkCtRBQdkjbBZyFHbz5i/p4bAIx/oxwudsanbVHxUYza8zmFA8zYxkP1og21HZgSYP1AiA2F/FWelagJIYQQQqQASSzEC8njbMvYduUAmLXzGt4B2pIoh7p1GVxzGEa9kaP3j3LQ/2DiE5qMhpzFpSTqJfiHRDPol1MkmC28USk/LcvnTdT+7fFvuRV1h4X98pFz3kycXmui7WTXOLi5R5VAtZ8HeoP2HCGEEEKIlySJhXhhHat60LS0O3EmM5+sSbokysPRgx6lulPphpmZx6ZhMv9t/wtre3jzSUnUCvDekXbBZ2Ix8SbeX3GSR5FxlMnnzDedKqL727yIXbd3se7aOnTomNRoCnlee13byfm1aslfgPbfQ56yaRS9EEIIIbILSSzEC9PpdEzq+KwkauH+pFeJ6vSzD6N/M1NwrzebbmxK3FioNtQepI6lJOo/WSwWRq+/wLm7objaG1nYqxp21s9GGh5EPWDzopG0PWqmT9ne1MhbQ9vJvXOwcbA6rjcMyssqUEIIIYRIeZJYiGTJ42zLmMclUTO9ki6JcqlVF7O1FXaxMPfMXKITohOf8NqXj0ui/GGHlET9m58O3WLdqbvodTC3e1UK5ny20Z3ZYmby1s/p+Uc47/xlpvftJCZiRwXB6p6QEA3Fm0LTMWkYvRBCCCGyE0ksRLJ1qurBa49Loj5NoiQqR9cuFNm6hZNNC/Ag6gG/XP4lcQfW9qocBx2cXgHXdqZd8JnIkZuP+HrLZQBGtipD/RJuidp/ufwLO8OPs6qpNbrqlcj5ZofEHZgSYE0fCPGFHEWg048yr0IIIYQQqUYSC5FsOp2OSR0q4GRrxdm7oSza75O43doaB49CDKk6BIAfz/9IUExQ4k4K14HaH6jjP4ZCTGhahJ5p+IVE8+EvpzCZLbSvnJ/3Hu+A/oR3sDczT84EnY4aA0ZRavlKdFbP7Vmxcyz47AWjA3T7FewT73khhBBCCJGSJLEQLyWviy1j2qoJwDO8vLmWRElU66KtqWspTo2T4Sw4u0DbyWtfQc5iEOYnq0T9TUy8ifeXq8naZfM5M6Vj4snasaZYJv4xAlN8LI0KNKJLqS6J2gE4twYOP96o8M15kKdcGj4DIYQQQmRHkliIl/ZWtQI0KZVbrRK19pymJMrkf4+Ppt1g4J9mDhxchW+Yb+IOEpVELYfrUhJlsVgYtf485/1CyWFvZMFzk7UBZh+eSvdFN5i8QseYwgO1ScW9c7BJjRZRfwSUezNtghdCCCFEtiaJhXhpOp2OyR0rqpKoOyH8eCBxSZTRwwOnho24WyoH8Zj46uBXxJviE3dSuO6zjdo2SUnUskO3+P2UHwa9ju97JJ6sDXDI7xD7D64kVzgUirIjZ478iTuIfASrHk/W9myuJsoLIYQQQqQBSSzEK8nrYstXj0uipnt5c/1B4pIoj6nfUeqnXwjL68ipB6cYf3h84h25AZp+BTmKqpKoHdn3hfDhG4/439PJ2qWp65l4srZvmC+jDozCJ6+OfZM7UnTeD1jlyvXsBFMCrO0Dob7qenZaJJO1hRBCCJFmJLEQr6xztQI0LpWbuAQzH69JXBKlt7OjqEtRpjaail6nZ7P3BhZfWJy4A2uHZxvnnfoZru9K2yeQAdwNjuLDX9Vk7Tcr5+fd+okna/tH+PPe9nd5FPOIkjlKMqj5l9hXrZq4E68x4MIfRtEAAB/tSURBVLPv2WRtuxxp+AyEEEIIkd1JYiFemSqJqoCTjSqJWvxcSRRAvfz1mHGzDuN+MTHv6Ey8bnslPqFwXag1UB1ns5KoJztrB0XGUS6/M5Ofm6wdEBnA8LV9+HD+XeqF52VB8wXYWdkl7uTsajjyvTruMF921hZCCCFEmpPEQqSIfC52T0uipiVREpXw4AEeW89Qyg9qelsYtX8UFx9eTNxJ0zGPS6Luwo6v0ir0dGWxWBj5+3ku+IWR08FaM1n7UfQj+nv1p/GWu5T0hxE7bMhl89yysf5n1JK9AA0+hrLt0+4JCCGEEEI8JomFSDGdqxegUUlVEvXJmnOYzM/mUhjz5KHA7Nm4jx+LrkVDYkwxDPlrCPcj7z/rwNrh8SpRwKmfskVJ1JKDt1h/Wk3WntujCgVyPJusHRobygCvAfiE+rC5fV6sWjShyNx56PR/+7WNfAir34aEGDVZu4ks2yuEEEKI9CGJhUgxfy+JOnMnhMUHbiZqd6hVk1xdu/Fdw+/wdPUkMDqQIX8NISo+6tlJRepBzcclUX98BDFhafgM0tahGw+Z9KearD2qdRnqFn82WTs8LpwBO/rjHeyNm50b895YSonZ87AuVOhZB0921g69o/YDkZ21hRBCCJGOJLEQKSq/qx1fti0DwNQd3lx/EKE5x9HakTn1pzNsqxWWc5f5fP/nmMymZyc0Gws5iqgXzF5ZsyTqbnAUg389jclsoUMVD/rVK/K0LSo+iiHb3qfdggs0u2bHjy1+pLBzYW0nXl/Brf1g7fh4srZrmsUvhBBCCPE8SSxEiutSvSANH5dEfbr2bKKSqCdsfvmDumdiGLHezMGbu5lxcsazxr+XRJ1cBjd2p03gaSQ6zsTA5WqydnkPZyZ3rPB0snZMgioRc99xhmrXLQzYaqKwJae2k7Or4Mg8dfzmfHAvk4bPQAghhBBCSxILkeJ0Oh1TOlbA0caK074hLElilahc772HQ906xI4aSLxRx0+XfmKt99pnJxSpDzUHqONNQyA2XNNHZqQma5/jon8YuRysWdCrOrZGVb4UZ4pj2O5hHLt/jP21HTF3fJ1Cc+dileO5ZWP9z6gyMYCGn0LZN9L2SQghhBBCJEESC5Eq8rva8WWbJyVRV7kRmLgkSm9vT8HFi2nS8SMGVR4EwMQjEzly78izk5qOBdfCqiQqi6wStfiADxvO+D+erF0VD1e1bGy8OZ5P9nzMQf+D2FnZ8X3z+ZSbNBOHOnUSd/D3ydolXofGo9LhWQghhBBCaEliIVJN1xoFaVDCjdgEM5+u0ZZEPSn/eb/i+3TM1ZTXj8YxYvdwboY+nvRt4/i3kqilmb4kavvF+0zeegWAL9uUoU5xtWu2yWxi1L6RFPhpF933w+wms6iap6q2g5hQWN3r8WTt4tBxIejlV1gIIYQQGYO8KhGpRqfTMaVTRRxtrDjlG8J3269isWjnW1hiY3l71iV67zJT93AYg3cNJjgmWDUWbQA1+qvjjYMhSFtWldFZLBbm77nB+ytOYjJb6FjVgz51iwBgtpgZc2gMPge20e6YhQ4HEqgUaK/t5NEN+LEZ+B4CayeZrC2EEEKIDEcSC5GqPFztGPN447wf9t7g49/OEptgSnSO3taWnD16YCjowYNyebkTfodhu4cRZ4pTJzQbp5ZTDburXlzfOZ7Gz+Llxfy/vfuOjqrO/z/+vJNkUkghCaTQQk8A6QGpsgqiIIJgA1mEL79FURCQXfdQ1IV1Adl13dXFhiLoLgJKsSFKFJJQpAdDExETEiExQAiJCalzf39EwmaZNGZSwNfjnDnHe+f9ufdz3749zju3FRQx8/1vWPz5t5gmjOsVxuJ7i9+sbZomC3Yt4OOTH/N9M1cyHr+P4Dmz8ezcufRGfoiBN2+Dc9+Bb2OY8CkERdTOAYmIiIiUQY2FVLsHejRlwcibcLEYrI87zcPL9pCRk18qJmDCeFpt+Ig/jV6Kt5s3B9IOMP/r+cVnONy9YcJnENIJcs7BO8PgyIZaOprKS8vMZfTSXSUvwHtuRAeeu+cm3FwsmKbJX/f+lfePr8HAYEG/BfSe9hwBDz9ceiN73oR/j4TcDGgcCZO2QKMutXE4IiIiIuVSYyE1YuzNYbw9oQfe7q7sTkhn1Ks7OXU+u+R7wzBw8a5Hq/qteGHACzQ7Z7Dt4EcsO7ysOMA3FP5vE7QdUnzj8gcTYPs/wM6lVXXB4dMXGfHKDg4mZ+Dn6ca/J/ZkXO/mJd//K+5fnPrgXWZusPHnHs9wV8u7Sm+gqAA+nQmf/QHMIuj0IEzYCD4hNXsgIiIiIpWkxkJqzIC2DVn7WG8a+Xnww7lsRr66k32J6VfFdTntxuKVFv64tojXd/2TzYmbi79w94bRK+Hmx4qXv5wHn0wr/hFeh2yMT+G+13eScjGXVg3r8dGUvvRpfeWt2m988wardy9l0uc2eh03GRBf+tIwctLhP6Ng3zLAKL4UbOQb4OZRo8chIiIiUhVqLKRGRYT48uGUvnRs7Ed6dj4PvbWbj785UyrGLSQEq7sXfn5BuBbB3O1zOXzucPGXFhcY8jwM+SsYFjjwLqy8r/iJSbXMZjP555ffMeW9A+QW2BjQtiEbpvSleYN6JTHvHHmHJQeXkOVlkDh7NP4PjaH+Aw9c2cjZ48X3UyTEFr9Re8wq6Pck/PIELREREZG6So2F1LggXw/WPNqL29sHk19oY9qqOJZsOVHyxChrs2aE/eff9FrzOd1a30JuUfHbqFOzU69s5OZHYfQqcKsHP0TDssFw4VTtHBCQk1/I1FUH+OeXJwCY1L8Fb0/oga+HGwAZuRn8ZddfeGHv3wCY2mUqIx/6EyHPPotx+ZGxJ6KKb06/kAD1m8H/i4LwIbVyPCIiIiJVpcZCaoWX1ZXXf9ud3/VrAcALm7/jqbXx5BfaAHBv1Qo3D0/+NuBvtPFvQ8HZs0yOmszBtINXNhJ+J0zcBD6hcPbb4h/lP+6v8WM5k3GJ+1//ms8OpeLmYvDX+zox9672uFgMCm2FvHfsPe5aP5TvP13FvJVFTAn7LY92fvTKBkwTdi6B9x6AvEwI6wuTtkJw+xo/FhEREZFrpcZCao2LxeDpYe15bkQHLAas3f8j49/ew8WcK/dM1HOrx9/P384rrxXhEX+CcZvGMTN6JkmZScUBoZ3hd19BcEfIToMVd8HRj2vsGA4kXWD4kh0cOZNJYD0r703qxQORTQHYeWYn939yP4v2LCIrP5Pffm2lfTKM+Oq/3kJemFf8fo7Nc8G0QbeHYdyHUK+B/R2KiIiI1FFqLKTWjevdnGXje1DP6sLXP5xn1Gs7SE7PAYpfLmc99D3WQrjDMxKLYSHqVBQjPhrB83ueL36Rnl/j4jMXbQZD4SV4/2HY8XK1PzFq/YEfGb10F+d+ziMixIcPp/SlR/MAkjKTeGLLE0zb+AgnL5ygvnt9nu79LDf/7U0CJ/2O4Dlzijfw81l4Zzgc/E/x/SJ3Pg93vwyu1mqdt4iIiEh1UGMhdcKtEUF8MLkPIb4enDybzT2v7OBA0gUMwyB04QL8x41jwu+X88HdH9CvcT/8MgpYdeQ/DF0/lLcOvUWui1vxPRc9JgEmRD0Dnz4JRYVOn2uRzeT5Td8y8/1vyC+0cXv7YNY91gd/bxsv7n+RER+N4FLUFl56o4hZZ3vx6chPeSD8AXy6RRL0+99j8fSE1EPw5q2QvAvc/WDsB9DrMd2kLSIiItet66axWLBgAX369MHLy4v69etXasyECRMwDKPUp1evXtU7Ublm7RsVPzGqQyNfzmfnM2bpLj47lILFw4OQuXMwLBba+rfl1dteYcnnjXh5uSsBp7N46cBL3P3h3Xyc+Bm2IYuL//KPAfuXF9+3kJvptDn+nFfIo//ex+sxJwGYemtrXhvblc1JnzBswzCWH15Ooa2QHjQn4Gfos+9nfK2+pTdy7FNYdgdcTIaAVjDpK2g9yGlzFBEREakN101jkZ+fz/33389jjz1WpXF33nknKSkpJZ/PPvusmmYozhDi58H7j/ZmYEQQeYU2Hl95gNdjTpY8MQogPzER67lMQi5ZeXzQ04TWCyU1O5W52+fy4MbRfN2sS/H7Lty84ORX8PadkJHs8NySzudw76s7+fJYGlZXCy+N7sKgrpcYu+khFn/1DJbUc4T5hvHKwFeYNH8DwU8/TbN338G4fBbCZoPYF2DNWCjIhpa/KW4qGrRxeG4iIiIitc21tidQWfPnzwdgxYoVVRrn7u5OSIjeVnw9qefuytKHI3nu06Os2JnI85u+5dT5bP484ibcXCy4t2xJq6jN5B77lvCuPRnUaSQrj63k5LIl7G16jEfSH6Fv4748ed/rhH/yFKQdgbcGwgMrqzyXs1l5fHEklU2HU9j1QzpFNpMgH3cWPdCUL1Je4ulvNtExwcbLH5mYLZvSdc16rL/cIxHw27FgK4KEbXD0Izj2Cfz8yyNzez4KdywEl+vmP0ERERGRct3wv2qio6MJCgqifv36DBgwgAULFhAUFFTb05IKuFgM5g3vQFigF899epRVe5I5mpLFkJtC6NkigI6N/ah3c08A3F3cecitLwmfv8BDFpj2uJUdp3ew8/RORnQfxtRvdxL80zFc/z2cjn59MI7mQ8v+4GO/4Uy9mMvnh1P47HAqexPTS90DHtmiHjd3OcSs3bPJLcrFwKBLt6H4bNiMe74VS+bP4OcDib80E99uhOyzVzbg7gu3/xki/6860yciIiJS427oxmLIkCHcf//9hIWFkZCQwDPPPMNtt93G/v37cXd3tzsmLy+PvLy8kuXMzOLr8wsKCigoKLA7pjpd3mdt7Lsu+G3PJjTyc+fJ9+P5JjmDb5IzAPB0s9C1aX0iw/zp0dyfDjbwuqU/FncP3hwznSXfLCEqKYoPT23mcx8Pxnl1ZmJiPC3PfQkbvgTADGiJrUkvcpr24JRPBJuSbUR/n8Kxn85jWPLBko+Ldz5NA12JCLXSrKHBltOf8vG+FDqdNino152nuj9FREAEuaH34eGRhiV6LuaJTRiXLpQcg+lRH7PtUGwRwzBbDABXd7iO/33+2mvSWZRH51EunUN5dB7l0jmUR+dwNI9VGWeYZjU/k7Mc8+bNK7nEqSx79+4lMjKyZHnFihXMmDGDjIyMKu8vJSWFsLAwVq9ezahRo6o0p/feew8vL68q71Oc43wuxKcbnMw0+CHLILuw9NOTXAyTZt7Q1quAMH8XWvqYXMg9Sds33mFj10K+6mLgabESWGRQYOaTZxRxyTDINQzMKjyJKfiCyV/ftmEtMkie8QQB1jM0ythHSGYcbkU5JXF5rj6k+EVypn4k53zaYRo3dA8vIiIiN6icnBweeughLl68iK+vb7mxtfprZ+rUqYwePbrcmObNmzttf6GhoYSFhXHixIkyY2bPns3MmTNLljMzM2natCmDBw+uMJnVoaCggKioKG6//Xbc3NxqfP91kc1mcvJcNnsTLxR/Tl3gp8w8ErIgIcsKP4HFgMkp52mUls/og4Ec7+NLUm4yhUUmLVPBYjM40vzKswv6H7bR5oyN+HA43Rg8bSaNLhqM+ciCzc2Vj//QHQ/vYFp3bEb9HZ9gpKdx64m/4OGVVbINs14Qtoi7MSOGYWnWm8YWVxrXRoKqmWrSOZRH51EunUN5dB7l0jmUR+dwNI+Xr96pjFptLBo0aECDBjX3huHz58+TnJxMaGhomTHu7u52L5Nyc3Or1aKu7f3XNe0bW2nf2J/xfYtfopecfok9iensSTjPnoR0Es/nsDSoJ8mdbKR6BXIkri0BgT9S/0wK8zetJd2jHuNHTCeyWTCD2zXllj1LKNi/hfEtexDgegGS95Kfkc/Js8EYLrm8uGdd8f0RRQUUtc7FYjWLXznh2wTaD4f2IzCa9MTFct08aM1hqknnUB6dR7l0DuXReZRL51AeneNa81iVMdfN9RlJSUmkp6eTlJREUVERBw8eBKB169Z4e3sDEBERwaJFixg5ciQ///wz8+bN49577yU0NJTExETmzJlDgwYNGDlyZC0eiTibYRg0C/SiWaAX93VvAsBPmbnsSUhnT0IrTiSmQ2oW6efDsNp8OBcQikdQQ/b+8UH86xU/weli+lDyWrXG4zcDoFs3KMzH9dRemoVvwHLhGBTlQF5xx+4S0hzaDYf290DjbnqpnYiIiAjXUWPx7LPP8s4775Qsd+3aFYCtW7fym9/8BoDjx49z8eJFAFxcXDh06BDvvvsuGRkZhIaGcuutt7JmzRp8fHxqfP5Ss4J9Pbi7cyPu7twIgAvZ+Rw7k8Gp+K/p9cIXV3XffsPuAu66ssLViqVVX+q16lu8bCuCtKNgWCCovZoJERERkf9x3TQWK1asqPAdFv99H7qnpydffPFFNc9Krhf+9az0aO7P2aPXuAGLC4R0dOqcRERERG4kv54LwkVEREREpNqosRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYe51vYE6jrTNAHIzMyslf0XFBSQk5NDZmYmbm5utTKHG4Vy6RzKo3Moj86jXDqH8ug8yqVzKI/O4WgeL/8GvvybuDxqLCqQlZUFQNOmTWt5JiIiIiIitSMrKws/P79yYwyzMu3Hr5jNZuPMmTP4+PhgGEaN7z8zM5OmTZuSnJyMr69vje//RqJcOofy6BzKo/Mol86hPDqPcukcyqNzOJpH0zTJysqiUaNGWCzl30WhMxYVsFgsNGnSpLanga+vr/6jchLl0jmUR+dQHp1HuXQO5dF5lEvnUB6dw5E8VnSm4jLdvC0iIiIiIg5TYyEiIiIiIg5TY1HHubu786c//Ql3d/fansp1T7l0DuXROZRH51EunUN5dB7l0jmUR+eoyTzq5m0REREREXGYzliIiIiIiIjD1FiIiIiIiIjD1FiIiIiIiIjD1FjUAa+++iotWrTAw8OD7t27s23btnLjY2Ji6N69Ox4eHrRs2ZLXX3+9hmZat1Ulj9HR0RiGcdXn22+/rcEZ1z2xsbHcfffdNGrUCMMw+PDDDysco3q0r6q5VE3at2jRInr06IGPjw9BQUHcc889HD9+vMJxqsvSriWPqkn7XnvtNTp16lTyToDevXuzadOmcseoHq9W1TyqHitn0aJFGIbBjBkzyo2rrppUY1HL1qxZw4wZM5g7dy5xcXH079+fIUOGkJSUZDc+ISGBoUOH0r9/f+Li4pgzZw7Tpk1j3bp1NTzzuqWqebzs+PHjpKSklHzatGlTQzOum7Kzs+ncuTNLliypVLzqsWxVzeVlqsnSYmJimDJlCrt27SIqKorCwkIGDx5MdnZ2mWNUl1e7ljxepposrUmTJjz//PPs27ePffv2cdtttzFixAiOHDliN171aF9V83iZ6rFse/fuZenSpXTq1KncuGqtSVNqVc+ePc3JkyeXWhcREWHOmjXLbvwf//hHMyIiotS6Rx991OzVq1e1zfF6UNU8bt261QTMCxcu1MDsrk+AuWHDhnJjVI+VU5lcqiYrJy0tzQTMmJiYMmNUlxWrTB5Vk5Xn7+9vvvXWW3a/Uz1WXnl5VD2WLysry2zTpo0ZFRVlDhgwwJw+fXqZsdVZkzpjUYvy8/PZv38/gwcPLrV+8ODB7Ny50+6Yr7/++qr4O+64g3379lFQUFBtc63LriWPl3Xt2pXQ0FAGDhzI1q1bq3OaNyTVo/OpJst38eJFAAICAsqMUV1WrDJ5vEw1WbaioiJWr15NdnY2vXv3thujeqxYZfJ4merRvilTpnDXXXcxaNCgCmOrsybVWNSic+fOUVRURHBwcKn1wcHBpKam2h2TmppqN76wsJBz585V21zrsmvJY2hoKEuXLmXdunWsX7+e8PBwBg4cSGxsbE1M+YahenQe1WTFTNNk5syZ9OvXj5tuuqnMONVl+SqbR9Vk2Q4dOoS3tzfu7u5MnjyZDRs20L59e7uxqseyVSWPqseyrV69mgMHDrBo0aJKxVdnTbo6NFqcwjCMUsumaV61rqJ4e+t/baqSx/DwcMLDw0uWe/fuTXJyMi+88AK33HJLtc7zRqN6dA7VZMWmTp1KfHw827dvrzBWdVm2yuZRNVm28PBwDh48SEZGBuvWrWP8+PHExMSU+aNY9WhfVfKoerQvOTmZ6dOns3nzZjw8PCo9rrpqUmcsalGDBg1wcXG56q/qaWlpV3WSl4WEhNiNd3V1JTAwsNrmWpddSx7t6dWrFydOnHD29G5oqsfqpZq84oknnuDjjz9m69atNGnSpNxY1WXZqpJHe1STxaxWK61btyYyMpJFixbRuXNnXnrpJbuxqseyVSWP9qgeYf/+/aSlpdG9e3dcXV1xdXUlJiaGl19+GVdXV4qKiq4aU501qcaiFlmtVrp3705UVFSp9VFRUfTp08fumN69e18Vv3nzZiIjI3Fzc6u2udZl15JHe+Li4ggNDXX29G5oqsfqpZos/iva1KlTWb9+PVu2bKFFixYVjlFdXu1a8miPatI+0zTJy8uz+53qsfLKy6M9qkcYOHAghw4d4uDBgyWfyMhIxo4dy8GDB3FxcblqTLXWpMO3f4tDVq9ebbq5uZnLli0zjx49as6YMcOsV6+emZiYaJqmac6aNcscN25cSfwPP/xgenl5mU8++aR59OhRc9myZaabm5u5du3a2jqEOqGqefzHP/5hbtiwwfzuu+/Mw4cPm7NmzTIBc926dbV1CHVCVlaWGRcXZ8bFxZmA+eKLL5pxcXHmqVOnTNNUPVZFVXOpmrTvscceM/38/Mzo6GgzJSWl5JOTk1MSo7qs2LXkUTVp3+zZs83Y2FgzISHBjI+PN+fMmWNaLBZz8+bNpmmqHiurqnlUPVbe/z4VqiZrUo1FHfDKK6+YYWFhptVqNbt161bq8X/jx483BwwYUCo+Ojra7Nq1q2m1Ws3mzZubr732Wg3PuG6qSh4XL15stmrVyvTw8DD9/f3Nfv36mRs3bqyFWdctlx/n97+f8ePHm6apeqyKquZSNWmfvRwC5vLly0tiVJcVu5Y8qibtmzhxYsn/axo2bGgOHDiw5MewaaoeK6uqeVQ9Vt7/NhY1WZOGaf5yt4aIiIiIiMg10j0WIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiIiIiLiMDUWIiLidPPmzaNLly61tv9nnnmGRx55pFKxf/jDH5g2bVo1z0hE5MZnmKZp1vYkRETk+mEYRrnfjx8/niVLlpCXl0dgYGANzeqKn376iTZt2hAfH0/z5s0rjE9LS6NVq1bEx8fTokWL6p+giMgNSo2FiIhUSWpqask/r1mzhmeffZbjx4+XrPP09MTPz682pgbAwoULiYmJ4Ysvvqj0mHvvvZfWrVuzePHiapyZiMiNTZdCiYhIlYSEhJR8/Pz8MAzjqnX/eynUhAkTuOeee1i4cCHBwcHUr1+f+fPnU1hYyFNPPUVAQABNmjTh7bffLrWv06dP8+CDD+Lv709gYCAjRowgMTGx3PmtXr2a4cOHl1q3du1aOnbsiKenJ4GBgQwaNIjs7OyS74cPH86qVasczo2IyK+ZGgsREakRW7Zs4cyZM8TGxvLiiy8yb948hg0bhr+/P7t372by5MlMnjyZ5ORkAHJycrj11lvx9vYmNjaW7du34+3tzZ133kl+fr7dfVy4cIHDhw8TGRlZsi4lJYUxY8YwceJEjh07RnR0NKNGjeK/T9j37NmT5ORkTp06Vb1JEBG5gamxEBGRGhEQEMDLL79MeHg4EydOJDw8nJycHObMmUObNm2YPXs2VquVHTt2AMVnHiwWC2+99RYdO3akXbt2LF++nKSkJKKjo+3u49SpU5imSaNGjUrWpaSkUFhYyKhRo2jevDkdO3bk8ccfx9vbuySmcePGABWeDRERkbK51vYERETk16FDhw5YLFf+nhUcHMxNN91Usuzi4kJgYCBpaWkA7N+/n++//x4fH59S28nNzeXkyZN293Hp0iUAPDw8StZ17tyZgQMH0rFjR+644w4GDx7Mfffdh7+/f0mMp6cnUHyWREREro0aCxERqRFubm6llg3DsLvOZrMBYLPZ6N69OytXrrxqWw0bNrS7jwYNGgDFl0RdjnFxcSEqKoqdO3eyefNm/vWvfzF37lx2795d8hSo9PT0crcrIiIV06VQIiJSJ3Xr1o0TJ04QFBRE69atS33KeupUq1at8PX15ejRo6XWG4ZB3759mT9/PnFxcVitVjZs2FDy/eHDh3Fzc6NDhw7VekwiIjcyNRYiIlInjR07lgYNGjBixAi2bdtGQkICMTExTJ8+nR9//NHuGIvFwqBBg9i+fXvJut27d7Nw4UL27dtHUlIS69ev5+zZs7Rr164kZtu2bfTv37/kkigREak6NRYiIlIneXl5ERsbS7NmzRg1ahTt2rVj4sSJXLp0CV9f3zLHPfLII6xevbrkkipfX19iY2MZOnQobdu25emnn+bvf/87Q4YMKRmzatUqJk2aVO3HJCJyI9ML8kRE5IZimia9evVixowZjBkzpsL4jRs38tRTTxEfH4+rq249FBG5VjpjISIiNxTDMFi6dCmFhYWVis/Ozmb58uVqKkREHKQzFiIiIiIi4jCdsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYepsRAREREREYf9f+y6Rx83I+dAAAAAAElFTkSuQmCC", + "text/plain": [ + "<Figure size 800x500 with 1 Axes>" + ] + }, + "metadata": {}, + "output_type": "display_data" + }, + { + "name": "stdout", + "output_type": "stream", + "text": [ + "17.73%\n", + "16.68%\n", + "1.22%\n" + ] + } + ], + "source": [ + "import numpy as np\n", + "import matplotlib.pyplot as plt\n", + "\n", + "## Initiate Horizontal Axis\n", + "h = 0.1 # Step size\n", + "t = np.arange(0, 4, h)\n", + "\n", + "## Initiate Vertical Axis\n", + "# Wave parameters\n", + "A = 1.0 # amplitude\n", + "k = 0.5 # damping coefficient\n", + "omega = 2.0 # angular frequency\n", + "v = A * np.exp(-k * t) * np.cos(omega * t) # Velocity v(t)\n", + "\n", + "\n", + "# Finite difference methods (forward, backwards and central)\n", + "dvdt_fd = (v[1:] - v[:-1]) / h\n", + "dvdt_bd = (v[1:] - v[:-1]) / h\n", + "dvdt_cd = (v[2:] - v[:-2]) / (2*h)\n", + "\n", + "#Actual solution (Analytical)\n", + "dvdt_actual=A*np.exp(-k*t)*(-k*np.cos(omega*t)-omega*np.sin(omega*t))\n", + "\n", + "\n", + "# Plotting\n", + "plt.figure(figsize=(8, 5))\n", + "plt.plot(t, v, label='Velocity (m/s)', color='blue')\n", + "plt.plot(t[:-1], dvdt_fd, label='Forward difference')\n", + "plt.plot(t[1:], dvdt_bd, label='Backward difference')\n", + "plt.plot(t[1:-1], dvdt_cd, label='Central difference')\n", + "plt.plot(t, dvdt_actual, label='Analytical Solution',linestyle='dotted')\n", + "plt.title('Velocity of a pendulum in a viscous fluid')\n", + "plt.xlabel('Time (s)')\n", + "plt.ylabel('Velocity (m/s)')\n", + "plt.grid(True)\n", + "plt.legend()\n", + "plt.tight_layout()\n", + "plt.show()\n", + "\n", + "\n", + "max_error_fd = max(abs(dvdt_fd - dvdt_actual[:-1]))\n", + "max_error_bd = max(abs(dvdt_bd - dvdt_actual[1:]))\n", + "max_error_cd = max(abs(dvdt_cd - dvdt_actual[1:-1]))\n", + "\n", + "error = [max_error_fd, max_error_bd, max_error_cd]\n", + "\n", + "print(f\"{error[0]*100:.2f}%\\n{error[1]*100:.2f}%\\n{error[2]*100:.2f}%\")" + ] + } + ], + "metadata": { + "kernelspec": { + "display_name": "Python 3 (ipykernel)", + "language": "python", + "name": "python3" + }, + "language_info": { + "codemirror_mode": { + "name": "ipython", + "version": 3 + }, + "file_extension": ".py", + "mimetype": "text/x-python", + "name": "python", + "nbconvert_exporter": "python", + "pygments_lexer": "ipython3", + "version": "3.13.2" + } + }, + "nbformat": 4, + "nbformat_minor": 5 +} diff --git a/tutorials/module_3/numerical_differentiation.md b/tutorials/module_3/numerical_differentiation.md new file mode 100644 index 0000000..b34b315 --- /dev/null +++ b/tutorials/module_3/numerical_differentiation.md @@ -0,0 +1,67 @@ +# Numerical Differentiation +Finding a derivative of tabular data can be done using a finite difference. Here we essentially pick two points on a function or a set of data points and calculate the slope from there. Let's imagine a domain $x$ as a vector such that $\vec{x}$ = $\pmatrix{x_0, x_1, x_2, ...}$. Then we can use the following methods to approximate derivatives + +## Forward Difference +Uses the point at which we want to find the derivative and a point forwards on the line. +$$ +f'(x_i) = \frac{f(x_{i+1})-f(x_i)}{x_{i+1}-x_i} +$$ +*Hint: Consider what happens at the last point.* + +```python +import numpy as np +import matplotlib.pyplot as plt + +# Initiate vectors +x = np.linspace(0, 2, 100) +y = 34 * np.exp(3 * x) + +dydx = (y[1:] - y[:-1]) / (x[1:] - x[:-1]) + +# Plot the function +plt.plot(x, y, label=r'$y(x)$') +plt.plot(x, dydx, label=b'$/frac{dy}{dx}$') +plt.xlabel('x') +plt.ylabel('y') +plt.title('Plot of $34e^{3x}$') +plt.grid(True) +plt.legend() +plt.show() +``` + + +## Backwards Difference +Uses the point at which we want to find +$$ +f'(x_i) = \frac{f(x_{i})-f(x_{i-1})}{x_i - x_{i-1}} +$$ + + +```python +import numpy as np +import matplotlib.pyplot as plt + +# Initiate vectors +x = np.linspace(0, 2, 100) +y = 34 * np.exp(3 * x) + +dydx = (y[1:] - y[:-1]) / (x[1:] - x[:-1]) + +# Plot the function +plt.plot(x, y, label=r'$y(x)$') +plt.plot(x, dydx, label=b'$/frac{dy}{dx}$') +plt.xlabel('x') +plt.ylabel('y') +plt.title('Plot of $34e^{3x}$') +plt.grid(True) +plt.legend() +plt.show() +``` +## Central Difference + +$$ +f'(x_i) = \frac{f(x_{i+1})-f(x_{i-1})}{x_{i+1}-x_{i-1}} +$$ + + + diff --git a/tutorials/module_3/numerical_integration.md b/tutorials/module_3/numerical_integration.md new file mode 100644 index 0000000..e3dcbcf --- /dev/null +++ b/tutorials/module_3/numerical_integration.md @@ -0,0 +1,17 @@ +## Midpoint Method + + +## Trapezoidal Method + + +## Romberg Integration + + +## Gaussian Integration + + +## Simpson's Rule + +### Simpsons 1/3 + +### Simpsons 3/8 diff --git a/tutorials/module_3/ode.md b/tutorials/module_3/ode.md new file mode 100644 index 0000000..23b647c --- /dev/null +++ b/tutorials/module_3/ode.md @@ -0,0 +1,10 @@ +# Numerical Solutions of Ordinary Differential Equations + +## Euler's Method + +### Forwards Eulers + +### Backwards Eulers + +## Runge-Kutta + diff --git a/tutorials/module_3/roots_optimization.md b/tutorials/module_3/roots_optimization.md new file mode 100644 index 0000000..3a288cc --- /dev/null +++ b/tutorials/module_3/roots_optimization.md @@ -0,0 +1,12 @@ +# Root Finding Methods + +Root Finding Methods or non-linear equation solvers. + +## Incremental Search + +## Bisection + +## Modified Secant + +## Newton-Raphson + |
